【ラウールの法則】気液平衡とは？（理想溶液編）

気液平衡って何だろう？
ラウールの法則とどんな関係があるのかな？
学校で習った気がするけど、よく覚えてないな。

こんなお悩みを解決します。

どうも。こんにちは。
ケミカルエンジニアのこーしです。

本日は、「【ラウールの法則】気液平衡とは？（理想溶液編）」についてわかりやすく解説していきます。

この記事を読むことで、ラウールの法則や理想溶液、気液平衡を理解することができ、圧力と温度、組成の関係を説明できるようになります。

化学プラントにおいて、気液平衡の理解は「生命線」と言っても過言ではないです。

もし自信の無い方は、ぜひこの記事で勉強してみて下さい！

この記事を書いた人

こーし(@mimikousi)

気液平衡とは？

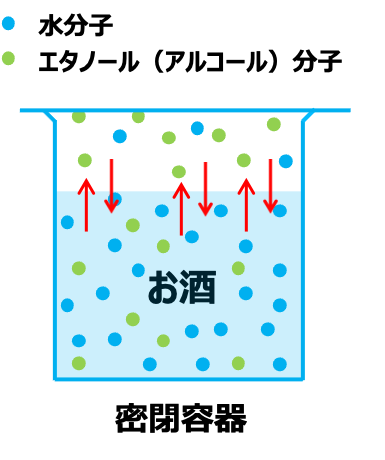
コップに入れたお酒（水とエタノールの混合物）は、長時間放置すると蒸発して無くなってしまいます。

しかし、密閉した容器にお酒を入れておくと、蒸発した分子がどこにも行けないので、ある程度多くなってくると、液体に戻ります。

蒸発する分子数と凝縮して液体に戻る分子数が等しくなったとき、これを気液平衡状態と言います。

気液平衡状態のとき、温度、圧力、濃度は安定しています。

蒸気圧とは

気液平衡が問題となるのは、液体の混合物（例えば、お酒）です。

１成分の場合は、「蒸気圧」だけで説明できます。

混合物の場合も、蒸気圧の理解が必要ですので、蒸気圧について、ポイントだけおさらいしておきます。

本記事では、「蒸気圧」は理解している前提で解説していきます。

もし、蒸気圧がよく分からない方は、こちらの記事も参考にしてみてください。

理想溶液とは

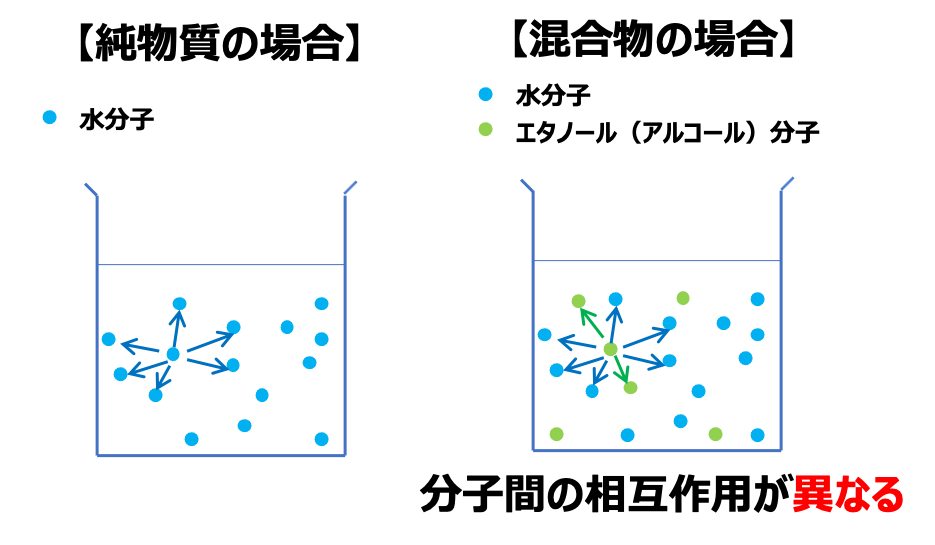
気液平衡は、混合物の組み合わせによって様々に変化します。

純物質の場合は、分子間の相互作用は等しいですが、混合物の場合は分子間の相互作用が分子の組み合わせで大きく異なります。

よって、混合物の場合は、分子間の相互作用を考慮して、気液平衡状態を推測します。

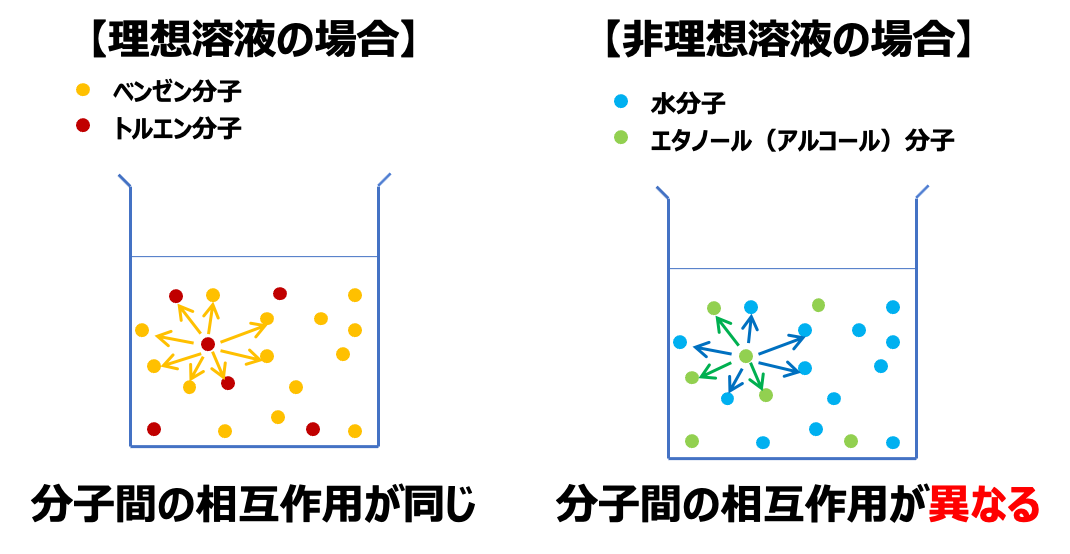
しかし、本記事では、混合物であっても分子間の相互作用が同じとみなせる「理想溶液」に着目して、解説していきます。

「非理想溶液」については、別記事で解説したいと思います。

ラウールの法則

２物質の混合溶液があるとき、ラウールの法則は下記のように表せます。

つまり、理想溶液の場合、物質の種類と温度で決まる「飽和蒸気圧」に、「液相のモル濃度」を掛けてやれば、「気相の分圧」が求まります。

これがラウールの法則です。非常に便利ですね。

ダルトンの分圧の法則

分圧と言われてもピンとこないかもしれませんが、これから紹介するダルトンの分圧の法則を知っていれば、分圧＝気相濃度と考えることができます。

ダルトンの分圧の法則とは、下記のように表せます。

よって、ラウールの法則とダルトンの分圧の法則を組み合わせると、全圧\(\pi\)は下記のように表すことができます。

この式は、非常に大事なので覚えておきましょう！

また、ダルトンの分圧の法則と理想気体の法則（\(PV = nRT\)）を使うと、分圧\(p_1,p_2\)から簡単に気相モル濃度（\(y_1,y_2\)）を求めることができます。

ちなみに、気体の体積\(V\)、気体の圧力\(P\)、気体の温度\(T\)、気体のモル数\(n\)、気体定数\(R\)とします。

混合気体の体積\(V\)、温度\(T\)は同じなので、（\(Ｒ\)も定数なので同じ）

分圧に理想気体の法則を使い、\(p_1V=n_1RT\)、\(p_2V=n_2RT\)　を変形すると、

$$n_1 = p_1\frac{V}{RT}$$

$$n_2 = p_2\frac{V}{RT}$$

となります。

\(\dfrac{V}{RT}\)は成分１と２で同じなので、全モル数は、

$$\begin{aligned}n_1 + n_2 &= \frac{p_1V}{RT} +\frac{p_2V}{RT}\\[5pt]
&=(p_1 + p_2)\frac{V}{RT}\end{aligned}$$

よって、気相のモル濃度（分率）\(y_1, y_2\)は、下記のように表すことができます。

ここまでが、気液平衡を理解するための前提知識です。

ここからが実務で使える気液平衡の考え方ですので、気合いを入れていきましょう！

定圧の気液平衡

蒸留塔など、気液平衡状態を一定圧力で制御している機器を考えましょう。

このとき、（３）式の全圧\(\pi\)は一定ということです。

ここで、液相の組成\(x_1,x_2\)を変化させるとどうなるでしょうか？

結論、温度が変化します。

なぜそうなるのか。理由を解説していきます。

気液平衡状態では、液相は沸点になっています。

つまり、全圧\(\pi\)と各成分の分圧の和が等しい状態です。

（わからなければ、蒸気圧を勉強しましょう）

（３）式を見てみると、変数は\(P_1,P_2,x_1,x_2\)の４つです。

ここで、各成分の飽和蒸気圧\(P_1,P_2\)は、成分の種類と温度だけで決まります。

よって、成分の種類は変化しないとすると、全圧\(\pi\)は液相温度\(T\)と各成分の液相モル濃度\(x_1,x_2\)で決まります。

気液平衡状態を一定圧力で制御している機器（蒸留塔など）では、液相モル濃度が変化した場合、温度が変化していると考えることができます。

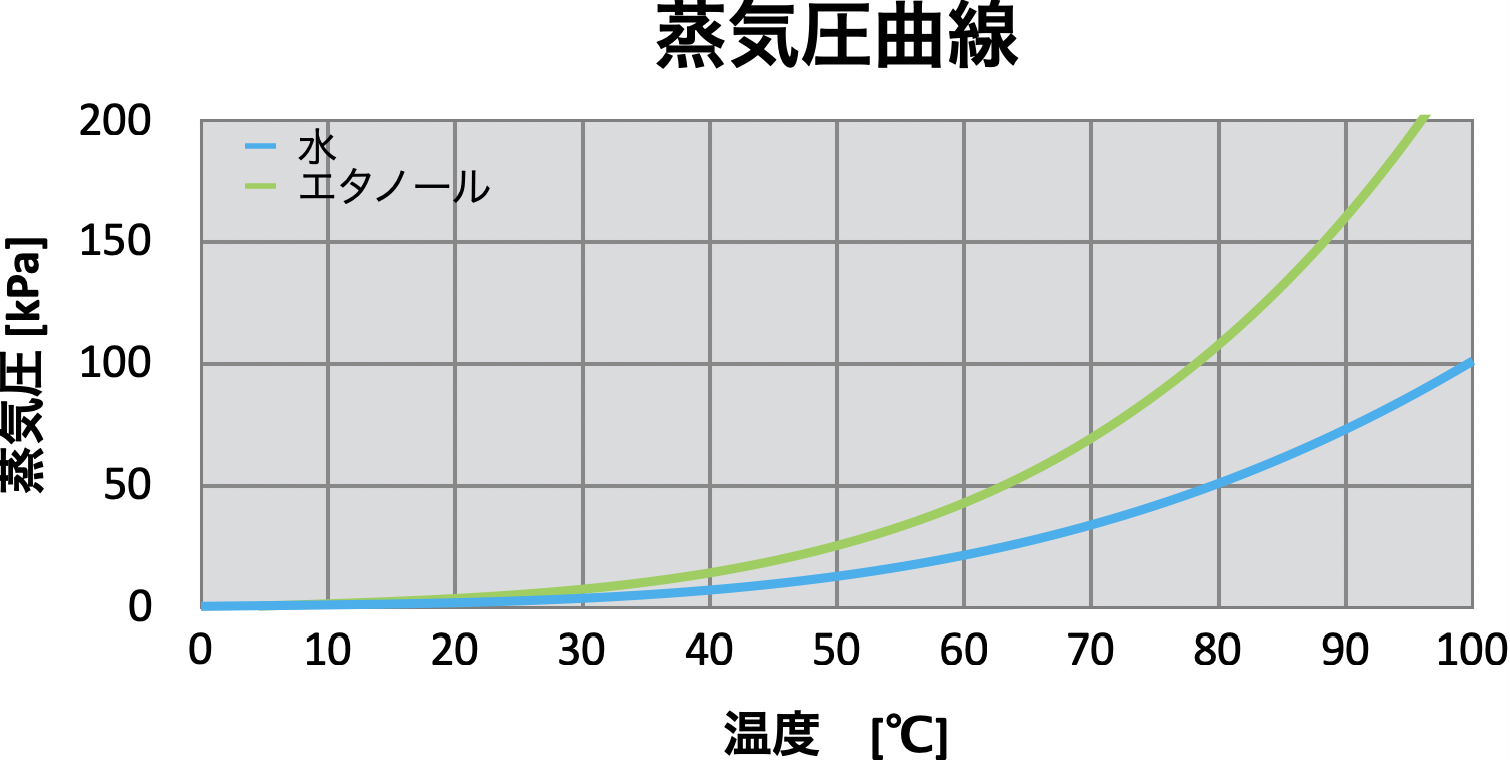
参考にエタノールと水の蒸気圧曲線を下図に示しました。

飽和蒸気圧\(P_1,P_2\)は、成分の種類と温度だけで決まるということが大事です。

実務において理想溶液を扱う機会は少ないと思います。
理想溶液の解説では、例題で具体的な計算をするより、定性的な説明をしておきます。
定性的な理解をしておく方が、非理想溶液の計算をする際に役立つと思います！

こーし

それでは、具体例を見てみましょう。

【定圧の気液平衡の具体例】

最もわかりやすいのは、蒸留塔の塔頂温度です。（定圧蒸留なら減圧でも大気圧でもＯＫ）

一定圧力で運転していて、塔頂温度が上昇する場合を考えます。

飽和蒸気圧は温度が上がると大きくなるのに、全圧\(\pi\)が一定ということは、蒸気圧の小さい（沸点が高い）高沸点成分が増えていることを示しています。

つまり、ボトムに溜まるべき高沸点成分が塔頂まで上がってきています。（分離が悪い状態です。）

例えば、蒸留塔の留出液が製品である場合、組成の変化は極力小さい方が良いです。

そこで、製品品質のバラツキを小さくするために、塔頂温度を還流量（還流比）で一定に制御することを考えます。

定温の気液平衡

反応器や蒸留塔（ボトム）など、液相温度を一定で制御している機器を考えましょう。

ここで、液相の組成を変化させるとどうなるでしょうか？

結論、圧力が変化します。

なぜそうなるのか。理由を解説していきます。

（3）式を見てみます。

仮に、\(x_1\)が低沸点成分だとすると、各成分の飽和蒸気圧は\(P_1 > P_2\)となります。

よって、蒸気圧の大きい低沸点成分（\(x_1\)）が多くなれば、全圧\(\pi\)は上昇します。

一方、蒸気圧の小さい高沸点成分（\(x_2\)）が多くなれば、全圧\(\pi\)は低下します。

つまり、液相温度を一定に制御しているとき、組成が変わると圧力が変化します。

【定温の気液平衡の具体例】

最もわかりやすいのは、蒸留塔のボトム温度です。（ボトム温度制御の場合）

フィード量が増加したとすると、蒸留塔の負荷も増加し、塔内の圧力損失が増大します。

すると、蒸留塔の塔底圧力も上昇します。

蒸留塔の塔底圧力が上昇する場合、ボトム温度を一定で制御していると、ボトム液の組成は低沸点成分が増えます。

なぜなら、全圧\(\pi\)（塔底圧力）が上昇しているのに、温度\(T\)が一定なので、蒸気圧の大きい低沸点成分が多くならないとバランスしないからです。

ボトム液の組成を極力一定に制御したい場合は、下記の検討が必要です。

まとめ

参考文献

①    とことんやさしい蒸留の本（大江修造著）

蒸留とは何か。をイメージしやすくしてくれた本です。

図が多くて読みやすいので、最初に読んでおけば、蒸留への抵抗がなくなるかもしれません。

②　絵とき蒸留技術　基礎のきそ（大江修造著）

蒸留の本で一番のオススメは、こちらの本です。

新入社員のときに、この本を読んで一気に蒸留が得意になりました。

③　蒸留技術大全（大江修造著）

大江先生の新刊です。（といっても2017年発売ですが）

これ1冊あれば、蒸留理論の基礎は完璧です。

内容は、絵とき蒸留技術　基礎のきそよりやや難しいですが、かなりの良書です。

省エネ技術、トラブルシューティングなどかゆいところにも手が届きます。

理解しやすい良書を見つけた場合は、著者買い（同じ著者の本をたくさん買う）するのがオススメです。

読書のコツでもあります。