
あと、そもそもなぜ「対数平均」を使う必要があるのだろう?
こんなお悩みを解決します。
どうも。こんにちは。
ケミカルエンジニアのこーしです。
本日は、「対数平均温度差(LMTD)の計算方法」について例題を用いてわかりやすく解説していきます。
本記事を読むことで、対数平均温度差を迷わず計算できるようになります。
また、なぜ「対数平均」を用いるのか?についても解説します。
化学工学の教科書だけでは学べない内容ですので、ぜひ一緒に勉強していきましょう!
本記事の内容
・対数平均温度差\(\Delta T_{lm}\)(LMTD)とは
・向流式と並流式
・対数平均温度差の計算例(例題)
・対数平均を用いる理由
この記事を書いた人
 こーし(@mimikousi)
こーし(@mimikousi)
目次
- 1 対数平均温度差\(\Delta T_{lm}\)(LMTD)とは
- 2 並流式と向流式
- 3 高温流体が状態変化している場合
- 4 対数平均温度差\(\Delta T_{lm}\)の計算例(例題)
- 5 【発展】なぜ対数平均を用いるのか?
- 5.1 Step1 微小区間\(\Delta z\)での高温流体の失う熱量\(\Delta Q\)を求める
- 5.2 Step2 熱交換器の伝熱速度式\(Q= UA\Delta T\)から\(\Delta Q\)を求める
- 5.3 Step3 微小区間\(\Delta z\)での低温流体の受け取る熱量\(\Delta Q\)を求める
- 5.4 Step4 \(\Delta Q\)を消去し、\(\Delta z\rightarrow 0\)の極限をとる
- 5.5 Step5 (7)式を\(z\)を\( 0\sim L\)まで積分する
- 5.6 Step6 熱交換器の熱収支式を求める
- 5.7 Step7 (9),(10)式を(8)式に代入する
- 6 参考文献
対数平均温度差\(\Delta T_{lm}\)(LMTD)とは
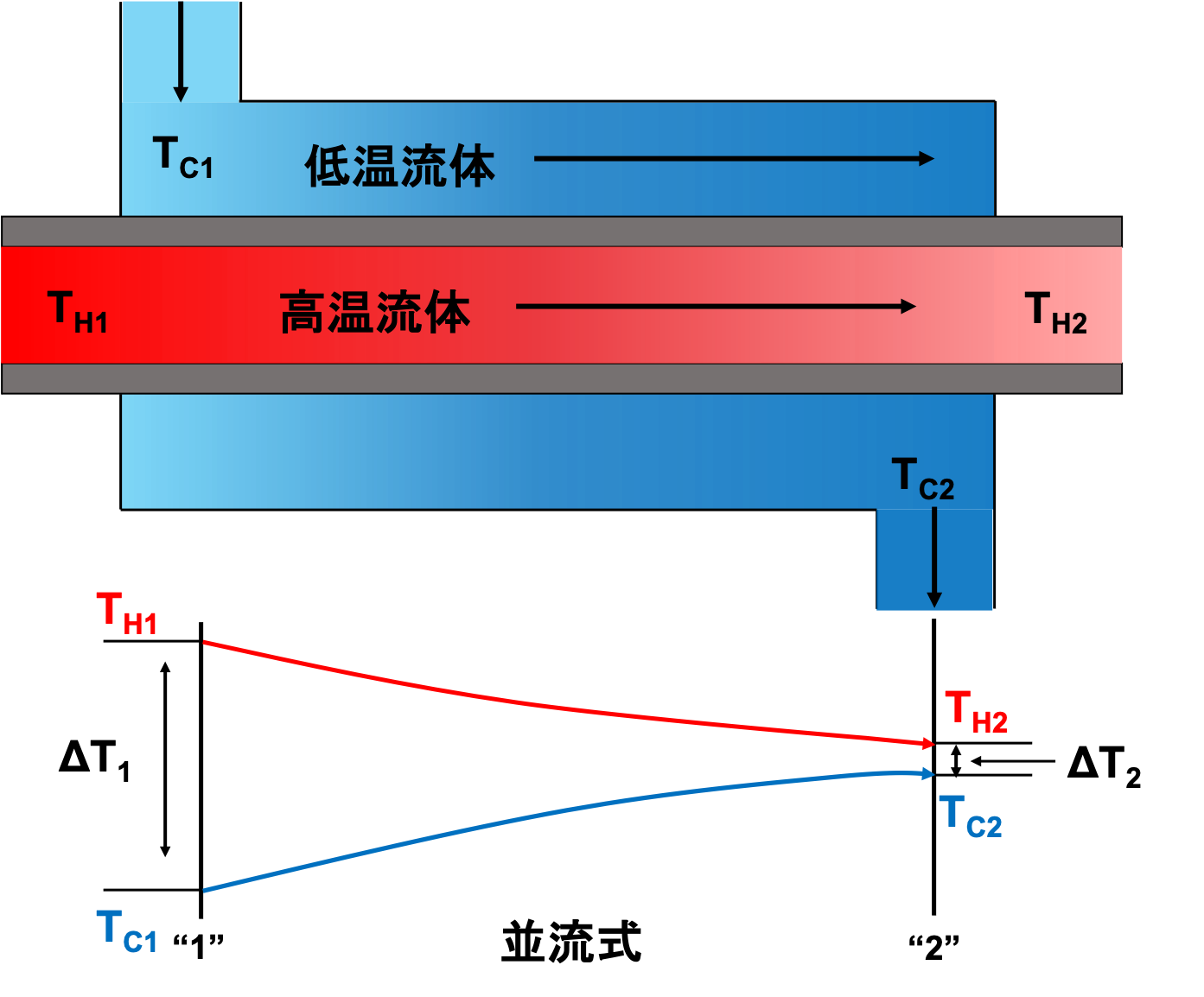
上図は、熱交換器の概略図です。
熱交換器では、高温流体から低温流体へ熱が移動しており、高温流体は温度が下がり、低温流体は温度が上がります。
よって、熱交換器の位置によって高温流体と低温流体の温度差\(\Delta T \)が異なってきます。
そのため、熱交換器全体の"平均"温度差を考える必要があり、そこで登場するのが対数平均温度差\(\Delta T_{lm}\)です。
対数平均温度差\(\Delta T_{lm}\)は、下式のように書けます。
対数平均温度差(LMTD)
$$\Delta T_{lm} = \frac{\Delta T_1 - \Delta T_2}{\ln \left(\frac{\Delta T_1}{\Delta T_2}\right)}\tag{1}$$
ちなみに、対数平均温度差\(\Delta T_{lm}\)は、英語ではLogarithmic Mean Temperature Differenceと書けますので、頭文字を取ってLMTDとも呼ばれます。

並流式と向流式
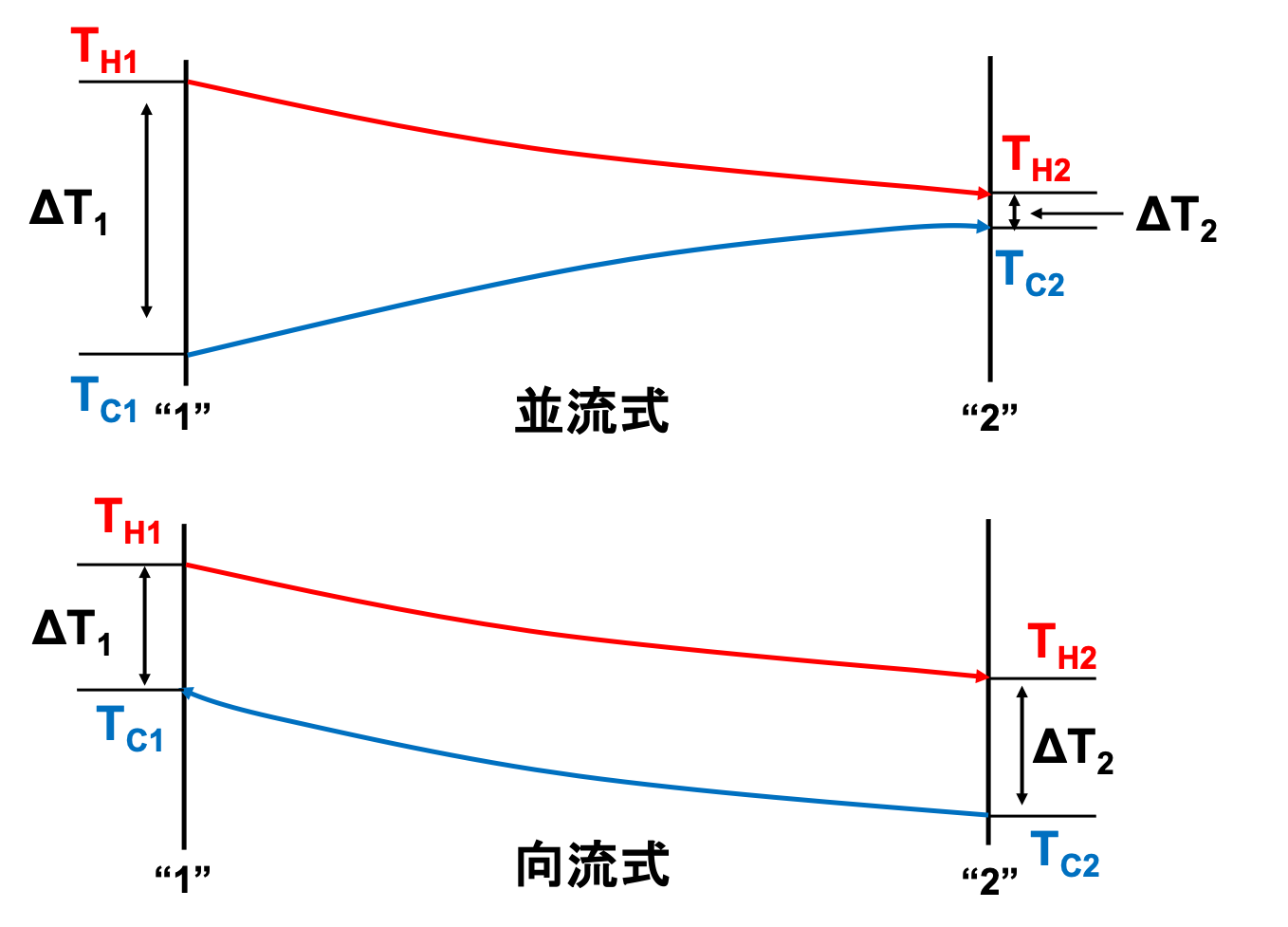
熱交換器には、並流式と向流式があります。
高温流体と低温流体を「並流」で流すのか、「向流」で流すのかの違いです。
上図からわかるように、向流式は温度差\(\Delta T\)に大きな変化はなく、伝熱量\(Q\)は熱交換器内でほぼ一定になります。
一方、並流式は低温流体の出口温度\(T_{C2}\)が高温流体の出口温度\(T_{H2}\)に漸近してしまうため、向流式に比べて、熱交換量が小さくなる傾向があります。
よって、大半の熱交換器は、向流式で設計されています。
向流式の優れている点
- 並流式に比べて、温度差、すなわち単位面積あたりの伝熱量が一定となる。
- 低温流体の出口温度\(T_{C2}\)を高温流体の出口温度\(T_{H2}\)よりも高くできる。
- 並流式よりも伝熱量を多くすることができる。
伝熱量と温度差の関係は、下の記事で詳しく解説しているよ!
オームの法則のアナロジーの部分を参照してね。

-

-
【わかりやすい】総括伝熱係数(U値)とは?
続きを見る
高温流体が状態変化している場合
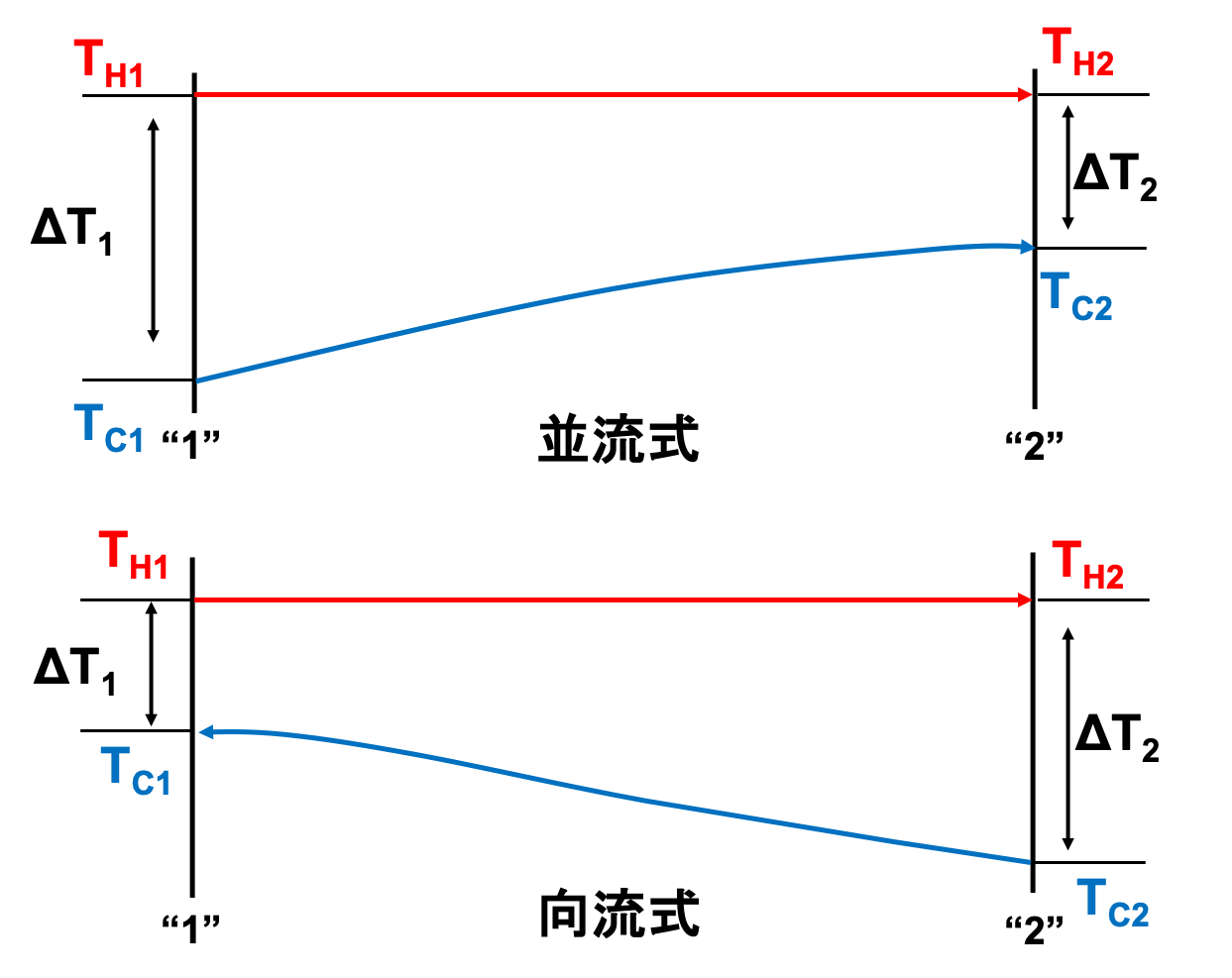
高温流体が熱交換器内で状態変化している場合、対数平均温度差\(\Delta T_{lm}\)は、並流式でも向流式でも変化しません。
熱交換器内で高温流体が状態変化していると、上図のように高温流体の温度は一定になります。
これは高校化学で習いましたね。(参考記事:物質の三態(スマナビング!)))
実務上、高温流体が一定になるのは、下記のような場合が考えられます。
具体例
- 飽和蒸気による加熱器
- 飽和蒸気の凝縮器

対数平均温度差\(\Delta T_{lm}\)の計算例(例題)
例題①
とある向流式の加熱器にて、130℃の熱媒を使用し、水を60℃から95℃に上昇させることを考えます。
熱媒は、熱交換器の出口で90℃まで低下しています。
このとき、対数平均温度差\(\Delta T_{lm}\)は何℃になるでしょうか。
それでは、早速例題を解いてみましょう!
高温流体(熱媒)は130⇒90℃となり、低温流体(水)は60⇒95℃になります。
向流式なので、下図のように書けます。
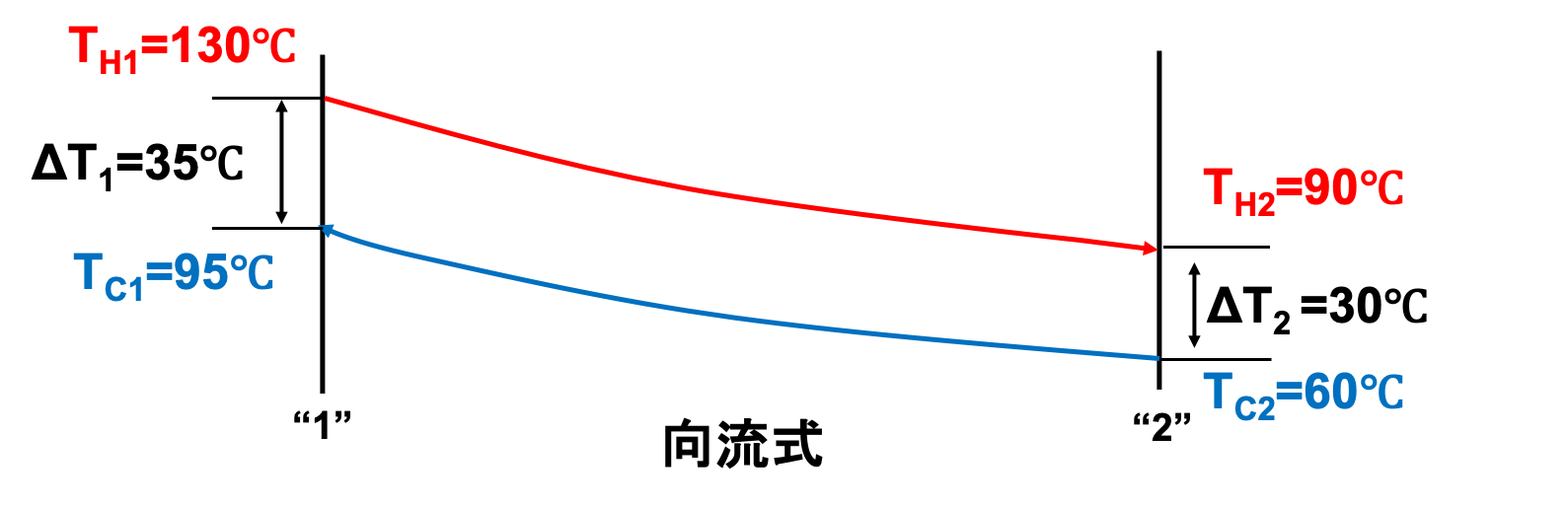
よって、対数平均温度差\(\Delta T_{lm}\)は、
$$\begin{aligned}\Delta T_{lm} &= \frac{\Delta T_1 - \Delta T_2}{\ln \left(\frac{\Delta T_1}{\Delta T_2}\right)}\\[5pt]
&=\frac{35-30}{\ln \left(\frac{35}{30}\right)}\\[5pt]
&=32.4℃(K)\end{aligned}$$

例題②
とある向流式の加熱器にて、140℃の飽和蒸気を使用し、水を40℃から80℃に上昇させることを考えます。
飽和蒸気は、熱交換器の出口ではドレンとなり、135℃まで低下しています。
このとき、対数平均温度差\(\Delta T_{lm}\)は何℃になるでしょうか。
高温流体(飽和蒸気)は140⇒135℃となり、低温流体(水)は40⇒80℃になります。
飽和蒸気の温度変化が小さいのは、気体から液体に状態変化する際の「潜熱」を低温流体に伝えているからです。
例題①と同様に、向流式なので下図のように書けます。
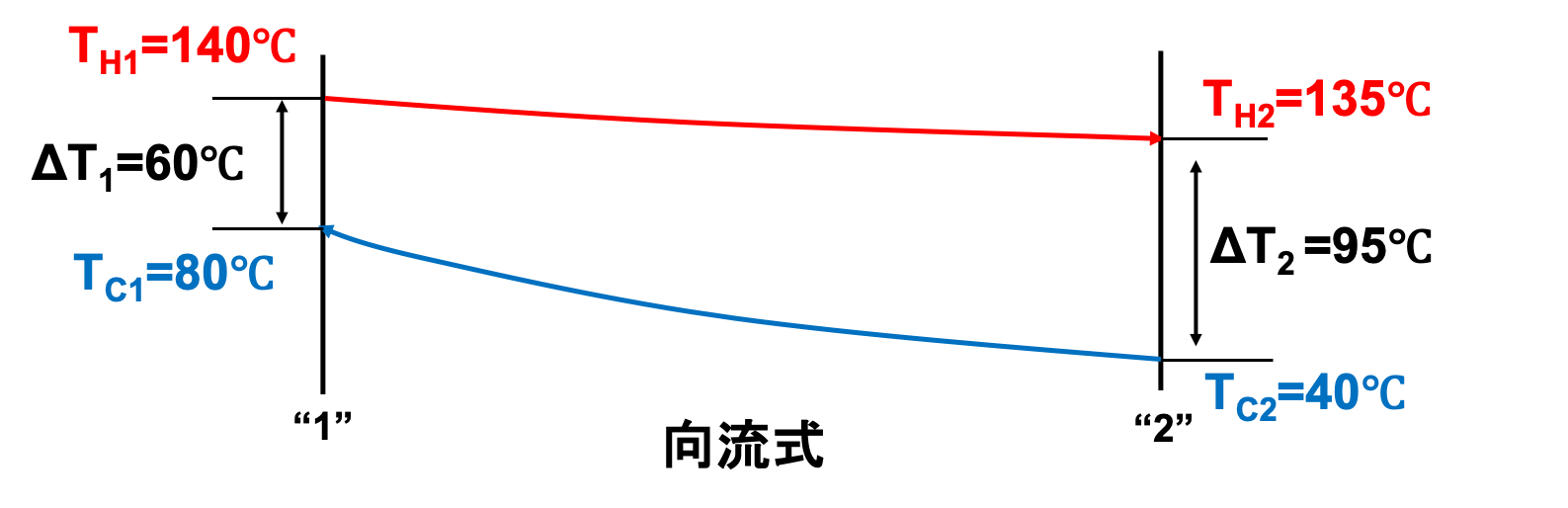
よって、対数平均温度差\(\Delta T_{lm}\)は、
$$\begin{aligned}\Delta T_{lm} &= \frac{\Delta T_1 - \Delta T_2}{\ln \left(\frac{\Delta T_1}{\Delta T_2}\right)}\\[5pt]
&=\frac{60-95}{\ln \left(\frac{60}{95}\right)}\\[5pt]
&=76.2℃(K)\end{aligned}$$
難しく考えなくても大丈夫!

【発展】なぜ対数平均を用いるのか?
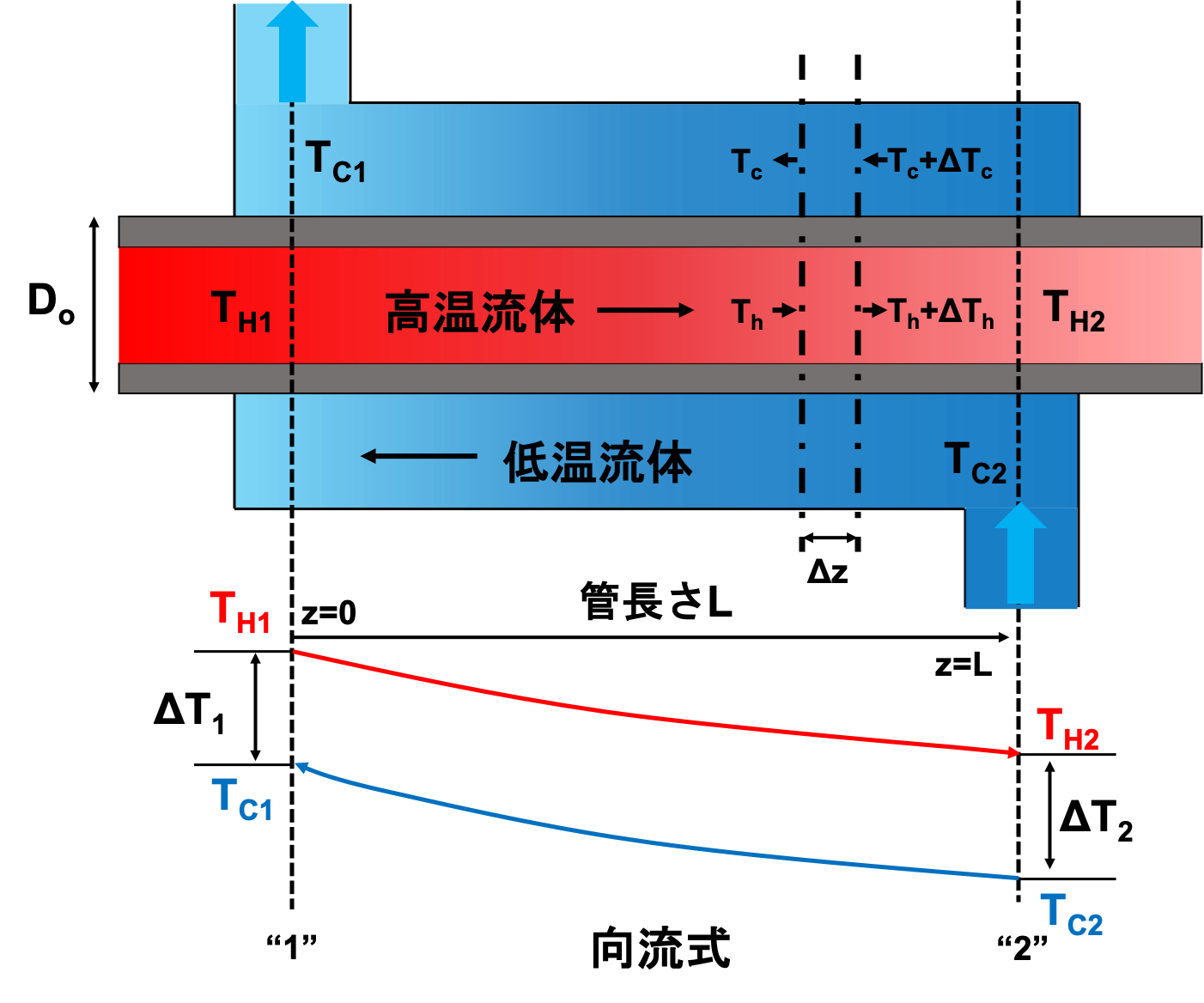
「なぜ対数平均を用いるのか」について、証明してみましょう!
上図に示した微小区間\(\Delta z\)で、高温流体と低温流体の熱収支を取り、\(z=0〜L\)まで積分すると、温度差が対数平均の形で表せます。
それでは、計算過程を極力省かずゴリゴリ計算していきます。
計算の手順
Step1 微小区間\(\Delta z\)での高温流体の失う熱量\(\Delta Q\)を求める
Step2 熱交換器の伝熱速度式\(Q= UA\Delta T\)から\(\Delta Q\)を求める
Step3 微小区間\(\Delta z\)での低温流体の受け取る熱量\(\Delta Q\)を求める
Step4 \(\Delta Q\)を消去し、\(\Delta z\rightarrow 0\)の極限をとる
Step5 (7)式を\(z\)を\( 0\sim L\)まで積分する
Step6 熱交換器の熱収支式を求める
Step7 (9),(10)式を(8)式に代入する
Step1 微小区間\(\Delta z\)での高温流体の失う熱量\(\Delta Q\)を求める
微小区間\(\Delta z\)における、高温流体の失う熱量は、下式のように書けます。
$$\Delta Q = -W_hC_{ph}\Delta T_h\tag{2}$$
記号の説明
\(\Delta Q\) [W]:高温流体の失う熱量
\(W_h\) [kg/s]:高温流体の流量
\(C_{ph}\) [J/(kg・K)]:高温流体の比熱
\(\Delta T_h\) [K]:高温流体の温度変化(<0)
Step2 熱交換器の伝熱速度式\(Q= UA\Delta T\)から\(\Delta Q\)を求める
続いて、熱交換器の伝熱速度式\(Q= UA\Delta T\)を用いて、微小区間\(\Delta z\)における、高温流体から低温流体に伝わる熱量を求めます。
$$\Delta Q = U\left(\pi D\Delta z\right)\left(T_h - T_c\right)\tag{3}$$
伝熱面積\(A\)は、\(A = \pi D \Delta z\)であり、温度差\(\Delta T\)は、\(\Delta T = T_h - T_c\)です。
記号の説明
\(U\) [W/(m2・K)]:総括伝熱係数
\(D\) [m]:管径
\(T_h\) [K] :微小区間\(\Delta z\)における高温流体の温度
\(T_c\) [K] :微小区間\(\Delta z\)における低温流体の温度
Step3 微小区間\(\Delta z\)での低温流体の受け取る熱量\(\Delta Q\)を求める
Step1と同様に、微小区間\(\Delta z\)における、低温流体の受け取る熱量は、下式のように書けます。
$$\Delta Q = -W_cC_{pc}\Delta T_c\tag{4}$$
記号の説明
\(\Delta Q\) [W]:低温流体の受け取る熱量
\(W_c\) [kg/s]:低温流体の流量
\(C_{pc}\) [J/(kg・K)]:低温流体の比熱
\(\Delta T_c\) [K]:低温流体の温度変化(<0)
Step4 \(\Delta Q\)を消去し、\(\Delta z\rightarrow 0\)の極限をとる
(2)、(3)式から\(\Delta Q\)を消去します。
$$- W_h C_{ph} \Delta T_h=U\left(\pi D \Delta z\right)\left(T_h - T_c\right)$$
ここで、\(\Delta z\rightarrow 0\)の極限を取り、\(\Delta z\rightarrow dz,\Delta T_h\rightarrow dT_h\)に変形すると、下式のように書き直せます。
$$\frac{dT_h}{dz}=-\frac{U\pi D\left(T_h - T_c\right)}{W_hC_{ph}}\tag{5}$$
同様に、(3)、(4)式から\(\Delta Q\)を消去します。
$$- W_c C_{pc} \Delta T_c=U\left(\pi D \Delta z\right)\left(T_h - T_c\right)$$
よって、上式についても\(\Delta z\rightarrow 0\)の極限を取って、\(\Delta z\rightarrow dz,\Delta T_c\rightarrow dT_c\)に変形すると、下式のように書けます。
$$\frac{dT_c}{dz}=-\frac{U\pi D\left(T_h - T_c\right)}{W_cC_{pc}}\tag{6}$$
(5)、(6)式をよく見てみると、\(T_h\)、\(T_c\)の微小変化\(dT_h\)、\(dT_c\)と、温度差(\(T_h - T_c\))が見つかります。
よって、(5)、(6)式の差を取ることで、\(\dfrac{d\left(T_h - T_c\right)}{T_h - T_c}\)の形を作ります。
$$\begin{aligned}\frac{d}{dz}\left(T_h - T_c\right)&=-U\pi D\left(T_h - T_c\right)\left(\frac{1}{W_hC_{ph}} - \frac{1}{W_c C_{pc}}\right)\\[5pt]
\frac{d}{dz}\left(T_h - T_c\right)&=\pi UD\left(\frac{1}{W_cC_{pc}} - \frac{1}{W_h C_{ph}}\right)\left(T_h - T_c\right)\end{aligned}$$
$$\frac{d\left(T_h - T_c\right)}{T_h - T_c}=\pi UD\left(\frac{1}{W_cC_{pc}} - \frac{1}{W_h C_{ph}}\right)dz\tag{7}$$
Step5 (7)式を\(z\)を\( 0\sim L\)まで積分する
(7)式の\(z\)を\( 0\sim L\)まで積分します。(温度は、\(T_{H1}\sim T_{H2}\)、\(T_{C1}\sim T_{C2}\)で積分)
この区間において、\(U,C_{ph},C_{pc}\)が一定であると見なすと、(7) 式は下式のように変形できます。
$$\begin{aligned}\int_{T_{H1},T_{C1}}^{T_{H2},T_{C2}}\frac{1}{T_h - T_c}d\left(T_h - T_c\right)&=U\left(\frac{1}{W_cC_{pc}}-\frac{1}{W_h C_{ph}}\right)\pi D\int_{0}^{L}dz\\[5pt]
\Bigl[ \ln \left(T_h- T_c\right) \Bigr]_{T_{H1},T_{C1}}^{T_{H2},T_{C2}}&=U\left(\frac{1}{W_cC_{pc}}-\frac{1}{W_h C_{ph}}\right)\pi D\Bigl [z\Bigr]_0^L\\[5pt]
\ln \left(T_{H2} - T_{C2}\right)-\ln \left(T_{H1} - T_{C1}\right)&=U\left(\frac{1}{W_cC_{pc}}-\frac{1}{W_h C_{ph}}\right)\pi DL\end{aligned}$$
$$\ln \frac{T_{H2} - T_{C2}}{T_{H1} - T_{C1}}=U\left(\frac{1}{W_cC_{pc}}-\frac{1}{W_h C_{ph}}\right)\pi DL\tag{8}$$
Step6 熱交換器の熱収支式を求める
高温流体側の熱収支式は、下式のように書けます。
$$Q = W_hC_{ph}\left(T_{H1} - T_{H2}\right)$$
ここで、少し変形すると下記(9)式となります。
$$\frac{1}{W_hC_{ph}}=\frac{\left(T_{H1} - T_{H2}\right)}{Q}\tag{9}$$
一方、低温流体側の熱収支式も下式のように書けます。
$$Q = W_cC_{pc}\left(T_{C1} - T_{C2}\right)$$
$$\frac{1}{W_cC_{pc}}=\frac{\left(T_{C1} - T_{C2}\right)}{Q}\tag{10}$$
Step7 (9),(10)式を(8)式に代入する
最後に、(9),(10)式を(8)式に代入し、\(Q=\)の式に変形します。
伝熱面積は、\(A=\pi DL\)なので、
$$\begin{aligned}\ln \frac{T_{H2} - T_{C2}}{T_{H1} - T_{C1}}&=U\left(\frac{T_{C1} - T_{C2}}{Q}-\frac{T_{H1} - T_{H2}}{Q}\right)\pi DL\\[5pt]
&=UA\frac{\left(T_{H2} - T_{C2}\right) - \left(T_{H1} - T_{C1}\right)}{Q}\\[5pt]
Q&=UA\frac{\left(T_{H2} - T_{C2}\right) - \left(T_{H1} - T_{C1}\right)}{\ln \frac{T_{H2} - T_{C2}}{T_{H1} - T_{C1}}}\end{aligned}$$
$$Q = UA \frac{\Delta T_2 - \Delta T_1}{\ln \frac{\Delta T_2}{\Delta T_1}}\tag{11}$$
(11)式の\(\dfrac{\Delta T_2 - \Delta T_1}{\ln \frac{\Delta T_2}{\Delta T_1}}\)は、分母分子に\(-1\)を掛けると、(12)式のように掛けます。
$$Q = UA \frac{\Delta T_1 - \Delta T_2}{\ln \frac{\Delta T_1}{\Delta T_2}}\tag{12}$$
よって、(1)式に示した対数平均温度差\(\Delta T_{lm}\)を用いると、
$$Q = UA\Delta T_{lm}\tag{13}$$
よって、熱交換器の伝熱速度式が導けました。
対数平均温度差(LMTD)
$$\Delta T_{lm} = \frac{\Delta T_1 - \Delta T_2}{\ln \left(\frac{\Delta T_1}{\Delta T_2}\right)}\tag{1}$$

参考文献
本記事では、P.198〜200を特に参考にしました。
この教科書では、「流動」「伝熱」「拡散」の理論を詳しく勉強できます。
化学工学の教科書を一通り学んだら、本書にも挑戦してみてください!
技術者としてレベルアップできること間違いなしです。
amazonなら、中古で安く購入できます。

