
わかりやすく解説するのでしっかり勉強していこう!

どうも。こんにちは。ケミカルエンジニアのこーしです。
本日は、「サンプルサイズの決め方(無相関検定)」について、わかりやすく解説します。
この記事を読めば、相関係数が「有意」と言えるまで、どのくらいのサンプルサイズが必要なのかがわかるようになります。
本記事の内容
- サンプルサイズの早見表
- 無相関検定(t検定)とは
- 標準誤差に基づくサンプルサイズの決定
- 検定力分析に基づくサンプルサイズの決定
- 参考文献
この記事を書いた人
 こーし(@mimikousi)
こーし(@mimikousi)
目次
サンプルサイズの早見表
無相関検定における必要なサンプルサイズは下記2通りの方法で算出します。
①検定力(検出力)曲線
②95%信頼区間

①検定力(検出力)曲線
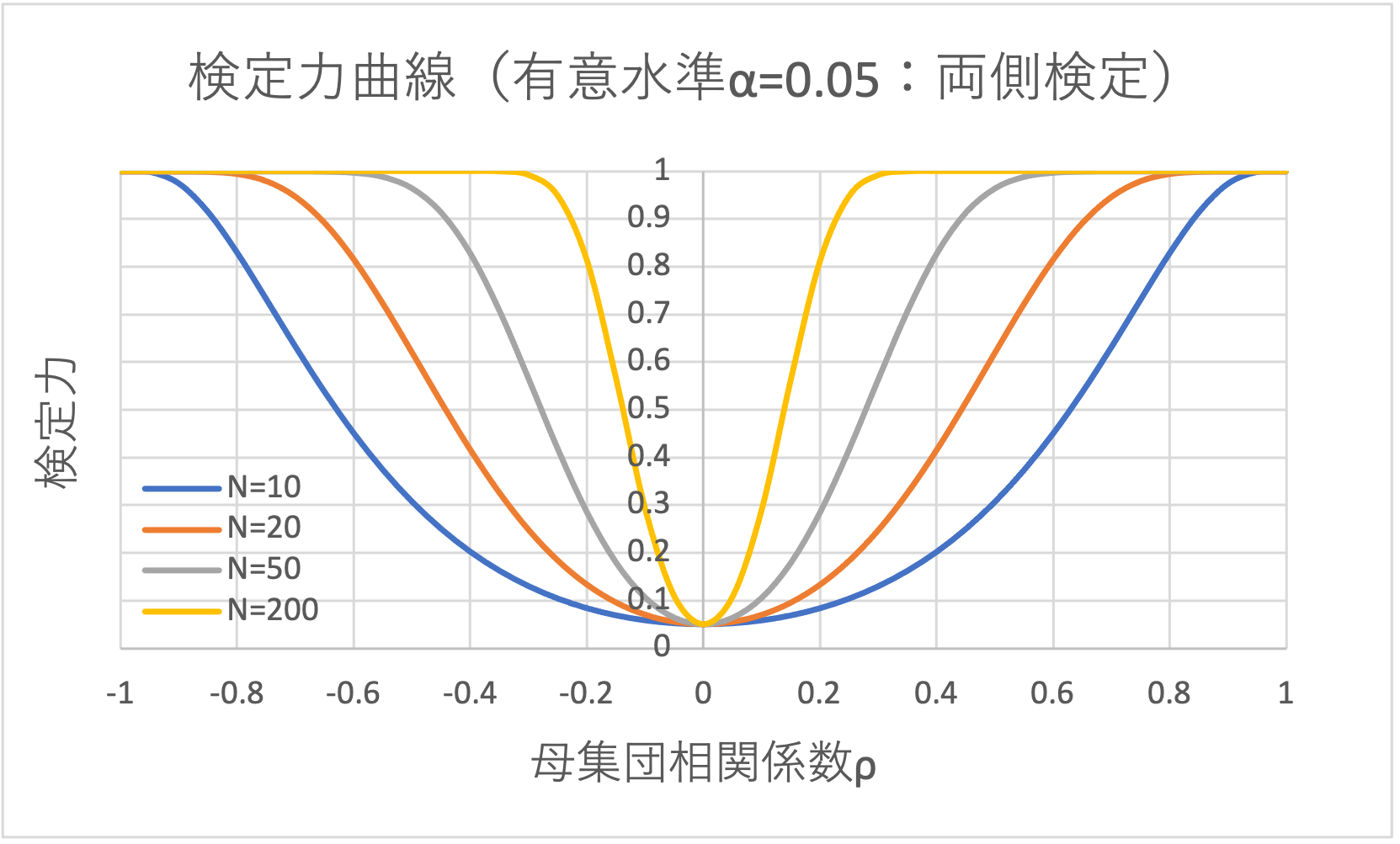
「検定力」については後述しますが、簡単に説明すると「相関があるときに無相関仮説を正しく棄却できる確率」のことです。
すなわち、検定力が小さいと相関があるにも関わらず、「相関なし」という検定結果が得られてしまいます。
上図の「検定力曲線」を見てみますと、サンプルサイズが大きくなるにつれて検定力も大きくなっていることがわかります。
ちなみに検定力は、有意水準\(\alpha\)と同様に前もって設定する基準です。
慣用的に、有意水準\(\alpha\)と検定力\(1-\beta\)は、下記の基準が用いられています。
・有意水準\(\alpha\)は、\(\alpha =0.05\)
・検定力\(1-\beta\)は、\(1-\beta=0.80\)
それでは、検定力\(1-\beta=0.80\)の時を考えてみましょう。
縦軸の\(0.8\)と検定力曲線の交点を見てみると、
\(N=10\)のときは、母集団相関係数は\(|\rho|=0.8\)程度となりますので、検定力を\(1-\beta=0.8\)以上にするには、母集団の相関係数が\(|\rho|=0.8\)以上である必要があります。
一方、\(N=50\)のときは、母集団相関係数は\(|\rho|=0.4\)程度となりますので、母集団の相関係数が\(|\rho|=0.4\)以上であれば、検定力を\(1-\beta=0.8\)以上にすることができます。
よって、母集団の相関係数がどのぐらいなのかを想定し、検定力曲線を用いることで、必要なサンプルサイズを求めることができます。
②95%信頼区間
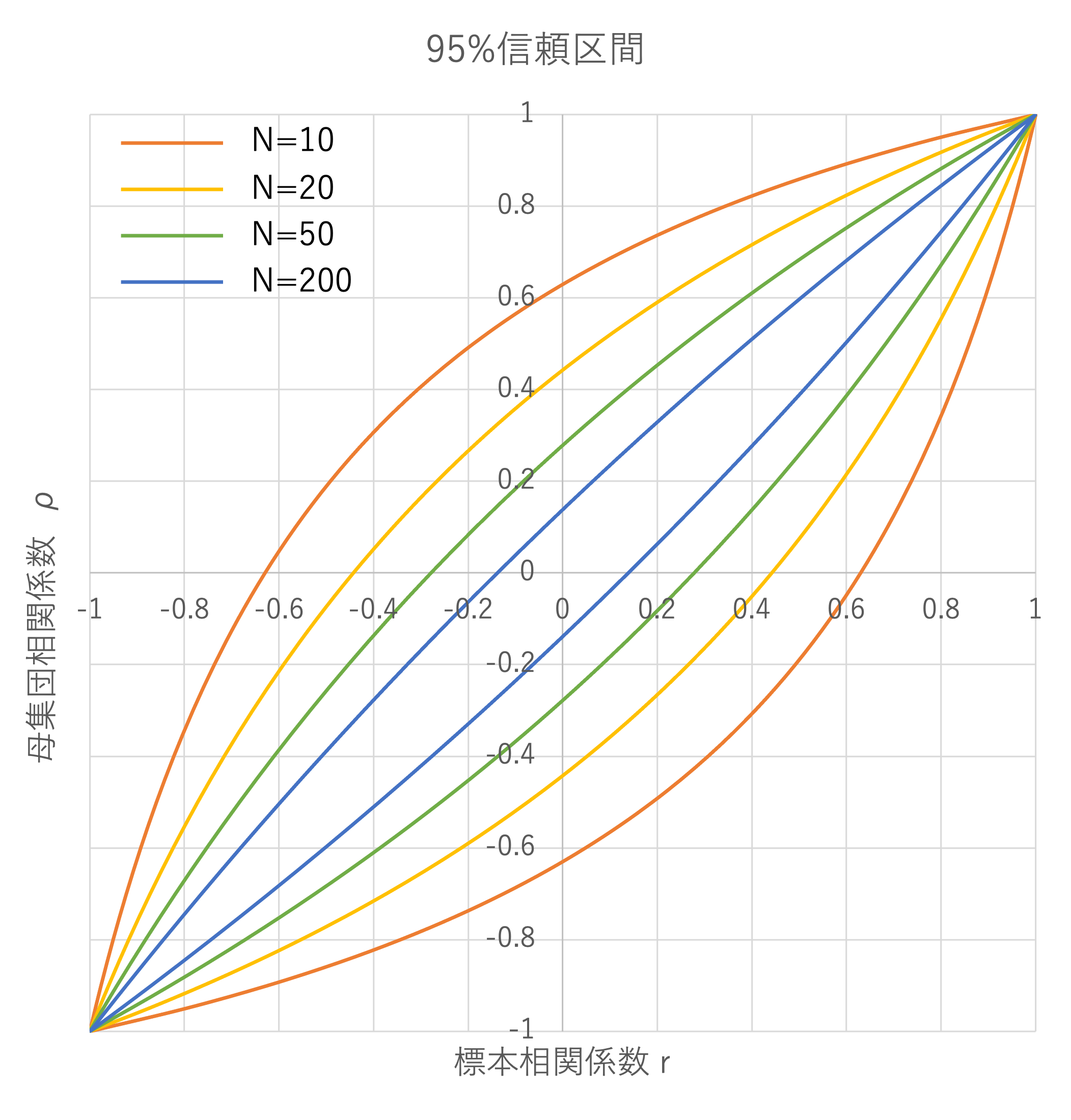
上図を見ていきますと、
サンプルサイズ\(N=20\)のデータから得られる標本相関係数が\(r=0.6\)のとき、母集団相関係数\(\rho\)の95%信頼区間は横軸の0.6と黄色の線の交点の範囲となります。
すなわち、\((0.214,0.824)\)の範囲となります。
同様に、サンプルサイズ\(N=200\)のときの95%信頼区間は\((0.503,0.682)\)となります。
よって、サンプルサイズが大きくなると95%信頼区間は狭くなり、より精度の高い区間推定が可能になります。
また、母集団相関係数\(\rho=0\)のときの標本相関係数\(r\)の95%信頼区間も上図から求めることができます。
サンプルサイズが\(N=10\)と少ないときの95%信頼区間は\((-0.630,0.630)\)となり、標本相関係数が\(r=0.6\)くらいあっても無相関の可能性が否定できません。
よって、標本相関係数が\(r=0.4\)以上ならば"有意である"とみなしたい場合、サンプルサイズは\(N=50\)程度にしないといけないことがわかります。
もっと詳しく学びたい方は下記内容も読んでみてね!

無相関検定とは
無相関検定は「母集団の相関係数はゼロである」という帰無仮説を設定し、得られたデータに基づいて棄却するかどうかを判断します。
一般に、無相関検定には2種類の方法があります。
無相関検定
①t分布を用いた検定(t検定)
②標本分布を用いた検定

①t分布を用いた検定(t検定)
t検定では、標本の相関係数\(r\)を用いて、下式により検定統計量\(t\)を求めます。
$$t = \frac{r}{\sqrt{1-r^2}}\times \sqrt{N-2}\tag{1}$$
上式は、「効果の大きさ」\(\dfrac{r}{\sqrt{1-r^2}}\)の部分と、「標本の大きさ」\(\sqrt{N-2}\)に分解して考えることができます。
t検定の手順
それでは、t検定の手順を見ていきましょう。
t検定の手順
- 仮説の設定
帰無仮説\(H_0:\rho = 0\)(母集団の相関係数はゼロである)
対立仮説\(H_1:\rho \neq 0\)(母集団の相関係数はゼロではない) - 検定統計量tの算出
$$t = \frac{r}{\sqrt{1-r^2}}\times \sqrt{N-2}\tag{1}$$ - 棄却域の設定
有意水準\(\alpha\)(基本5%)を決定
両側検定か片側検定を選択 - 判定
t分布表を読み取り、データから算出した検定統計量tが、
・棄却域に入る → 帰無仮説を棄却
・棄却域に入らない → 帰無仮説を採択 - 結論
一般に、相関がゼロかどうかに関心がある場合は稀で、少なくとも無相関仮説を棄却できる程度のデータが得られているかどうかを確認するために行います。
棄却できなかったので「判断を保留する」くらいのイメージですね。

例題(t検定)
ここで、サンプル数\(N=20\)で標本相関係数が\(r=0.6\)のときのt検定を行ってみましょう。
- 仮説の設定
帰無仮説\(H_0:\rho = 0\)(母集団の相関係数はゼロである)
対立仮説\(H_1:\rho \neq 0\)(母集団の相関係数はゼロではない) - 検定統計量tの算出
$$\begin{aligned}t &= \frac{r}{\sqrt{1-r^2}}\times \sqrt{N-2}\\[5pt]
&=\frac{0.6}{\sqrt{1-0.6^2}}\times \sqrt{20-2}\\[5pt]
&=3.18\end{aligned}$$ -
棄却域の設定
有意水準\(\alpha=0.05\)で、両側検定とする - 判定
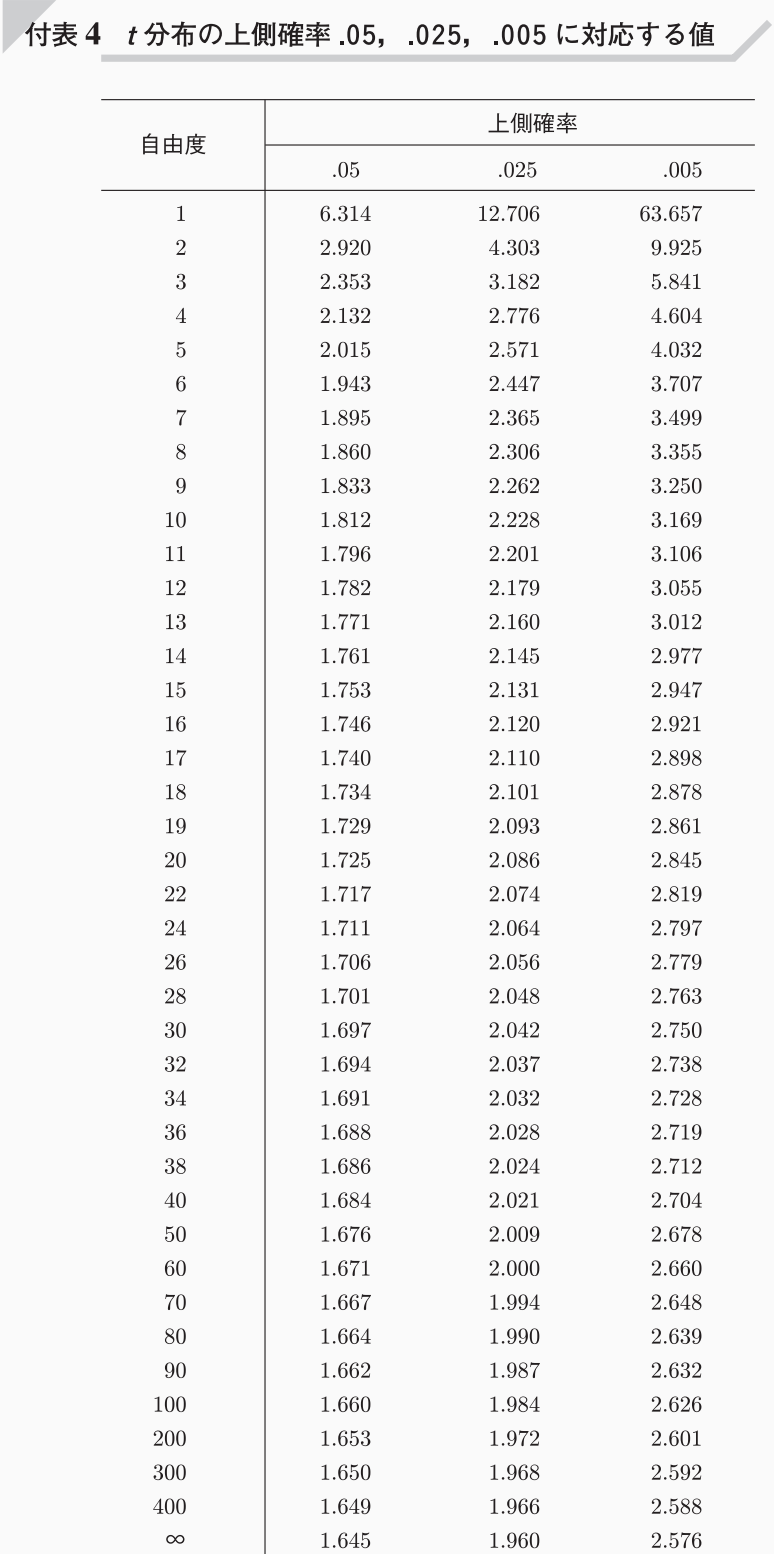
下記のt分布表から、自由度18(=20-2)、上側確率0.025より、
$$t_{0.025}(18)=2.101$$
よって、
\(t>t_{0.025}(18)\)となるため、有意水準\(\alpha=0.05\)の両側検定で有意となる。 - 結論
帰無仮説が棄却されるため、サンプル数\(N=20\)の標本相関係数\(r=0.6\)は有意である。
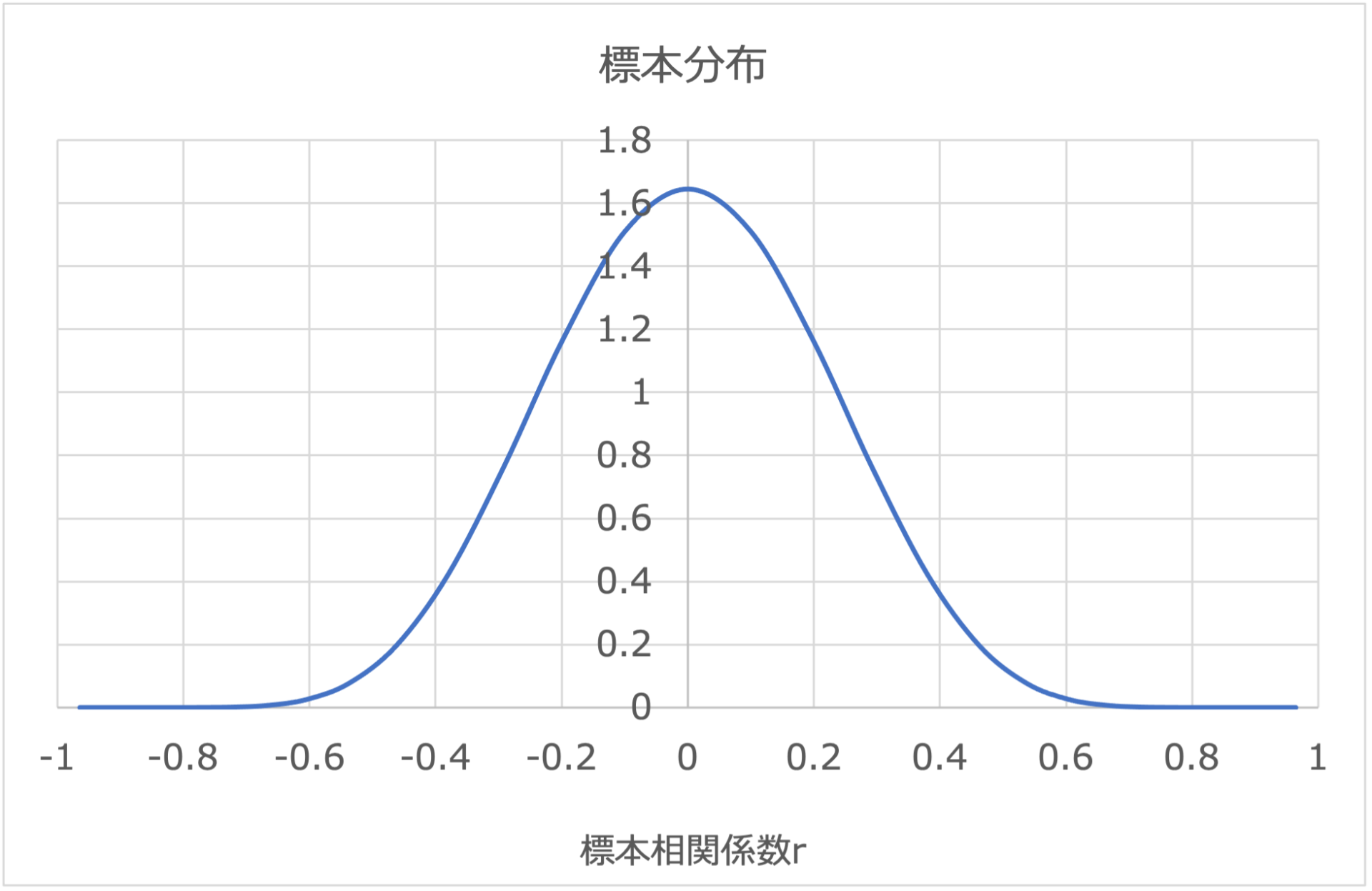
②標本分布を用いた検定
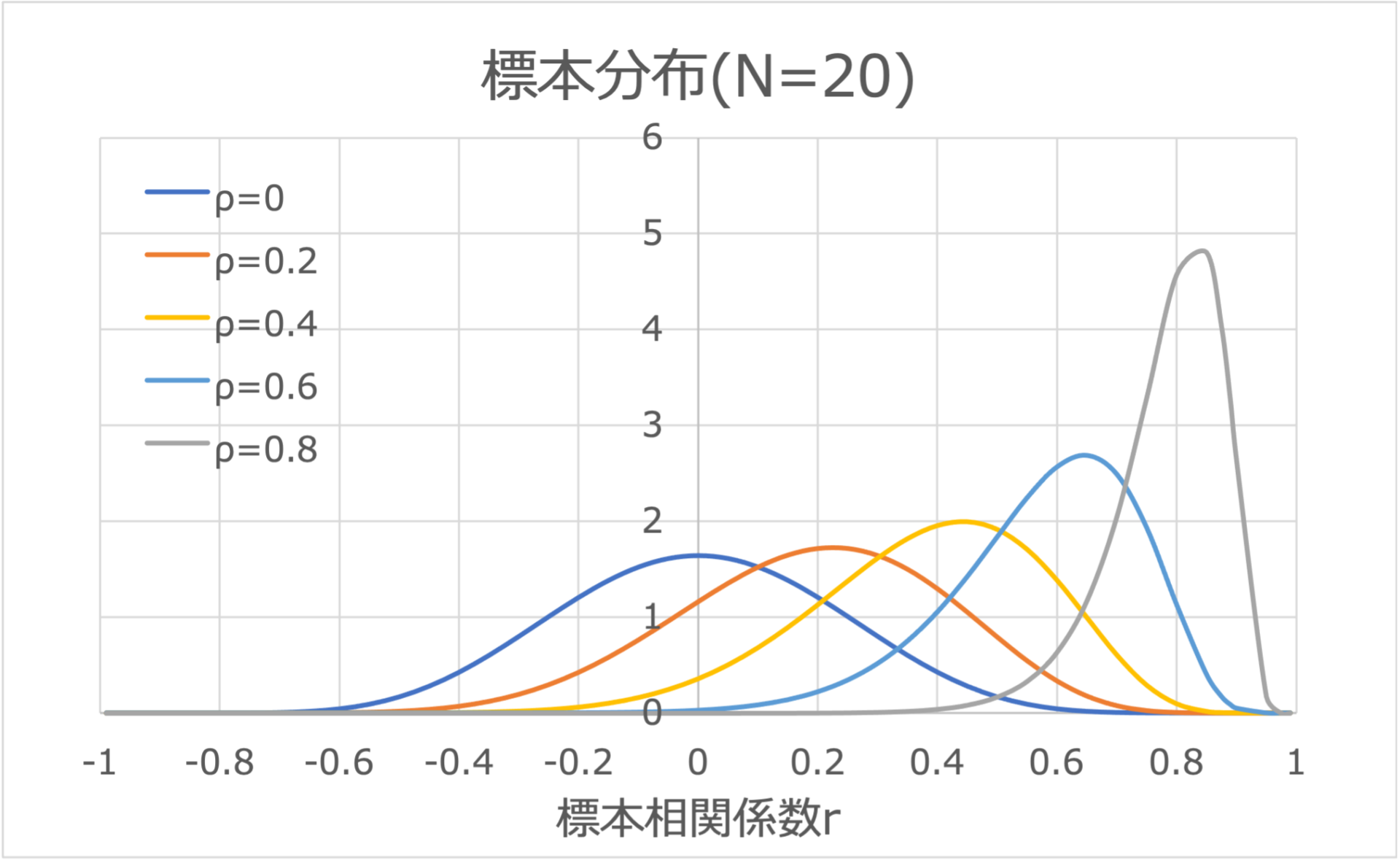
相関係数\(r\)の標本分布は、母集団相関係数\(\rho\)とサンプルサイズ\(N\)によって規定される確率分布です。
相関係数の確率密度分布はかなり複雑ですが、平均値\(\mu_r\)と標準誤差\(\sigma_r\)は近似的に下式のように書けます。
$$\mu_r =\rho - \frac{\rho(1-\rho^2)}{2N}\tag{2}$$
$$\sigma_r =\frac{1-\rho^2}{\sqrt{N}}\tag{3}$$
(1)式の右辺第2項は、「統計量の期待値」と「母数の値」との差を表しており、バイアス(bias)と呼ばれています。
サンプルサイズ\(N\)が大きくなると、バイアスが小さくなることがわかります。
(2)式からわかるように、相関係数\(r\)の標準誤差\(\sigma_r\)もサンプルサイズ\(N\)が大きくなると小さくなります。
また、母集団の相関係数\(\rho\)の絶対値が大きくなると、標準誤差\(\sigma_r\)は小さくなります。
図示してみると下図の通りです。
【参考】フィッシャーのz変換
相関係数\(r\)の標本分布は、フィッシャーのz変換と呼ばれる近似法にて求めることが出来ます。
$$\begin{aligned}Z&=\text{tanh}^{-1}r\\[5pt]
&=\frac{1}{2}\text{ln}\frac{1+r}{1-r}\end{aligned}\tag{4}$$
変数\(Z\)の標本分布は、母集団の相関係数\(\rho\)を用いると、下記の平均と標準偏差をもつ正規分布で近似できます。
$$\mu_Z = \text{tanh}^{-1}\rho = \frac{1}{2}\text{ln}\frac{1+\rho}{1-\rho}\tag{5}$$
$$\sigma_Z=\frac{1}{\sqrt{N-3}}\tag{6}$$
よって、変数\(Z\)の標本分布は正規分布\(N\left(\mu_Z,\dfrac{1}{N-3}\right)\)となります。
\(N\left(\mu_Z,\dfrac{1}{N-3}\right)\)に従う変数\(Z\)の確率密度関数は下式の通りです。
$$f(Z)=\frac{1}{\sqrt{2\pi\sigma_Z}}\text{exp}\left(-\frac{(Z-\mu_Z)^2}{2\sigma_Z^2}\right)\tag{7}$$
相関係数の標本分布の求め方(近似式)
- 標本相関係数\(r\)の範囲[-1,1]を指定する。
- (5),(6)式を用いて、平均\(\mu_r\)と標準誤差\(\sigma_r\)を求める。
(つまり、母相関係数\(\rho\)とサンプルサイズ\(N\)を決める。) - フィッシャーのz変換(4)式を微分する((8)式)。
- Zの正規分布(6)式を「変数変換」する((9)式)。
$$\begin{aligned}\frac{dZ}{dr}&=\frac{d(\text{tanh}^{-1}r)}{dr}\\[5pt]
&=\frac{1}{1-r^2}\end{aligned}\tag{8}$$
$$\begin{aligned}g(r)&=f(Z)\frac{dZ}{dr}\\[5pt]
&=f(\text{tanh}^{-1}r)\frac{1}{1-r^2}\\[5pt]
&=\frac{1}{\sqrt{2\pi\sigma_Z}}\text{exp}\left(-\frac{(\text{tanh}^{-1}r-\mu_Z)^2}{2\sigma_Z^2}\right)\frac{1}{1-r^2}\end{aligned}\tag{9}$$
例題(標本分布)
t検定と同様に、サンプル数\(N=20\)で標本相関係数が\(r=0.6\)のときの無相関検定を行ってみましょう。
まず、フィッシャーのz変換によりサンプル数\(N=20\)、母集団の相関係数\(\rho =0\)の標本分布を求めます。
(5),(6)式を用いて、平均\(\mu_Z\)と標準誤差\(\sigma_Z\)を求めます。
$$\begin{aligned}\mu_Z &= \frac{1}{2}\text{ln}\frac{1+\rho}{1-\rho}\\[5pt]
&=\frac{1}{2}\text{ln}\frac{1+0}{1-0}\\[5pt]
&=0\end{aligned}$$
$$\begin{aligned}\sigma_Z&=\frac{1}{\sqrt{N-3}}\\[5pt]
&=\frac{1}{\sqrt{20-3}}\\[5pt]
&=0.243\end{aligned}$$
よって、サンプル数\(N=20\)、母集団の相関係数\(\rho =0\)の標本分布は、平均\(\mu_Z=0\)、標準誤差\(\sigma_Z=0.243\)の正規分布となることがわかりました。
有意水準\(\alpha=0.05\)、両側検定での標準正規分布の棄却限界値は1.96なので、フィッシャーのz変換の棄却限界値は、下記のように求まります(\(z\sim N(0,1)\))。
$$\begin{aligned}P\left(|z|>1.96\right)=0.95\\[5pt]
P\left(z>1.96\right)+P\left(z<-1.96\right)=0.95\end{aligned}\tag{10}$$
フィッシャーのz変換を標準化して(10)式に適用すると、
$$P\left(\frac{Z-\mu_Z}{\sigma_Z}>\frac{Z_{0.025}-\mu_Z}{\sigma_Z}\right)+P\left(\frac{Z-\mu_Z}{\sigma_Z}<\frac{Z_{0.975}-\mu_Z}{\sigma_Z}\right)=0.95\tag{11}$$
よって、(11)式に平均\(\mu_Z=0\)、標準誤差\(\sigma_Z=0.243\)を代入すると、
$$\begin{aligned}\frac{Z_{0.025}-0}{0.243}&=1.96\\[5pt]
Z_{0.025}&=1.96\times0.243\\[5pt]
&=0.477\end{aligned}$$
$$\begin{aligned}\frac{Z_{0.975}-0}{0.243}&=-1.96\\[5pt]
Z_{0.975}&=-1.96\times0.243\\[5pt]
&=-0.477\end{aligned}$$
ここで、(4)式を変形して、
$$\begin{aligned}Z&=\text{tanh}^{-1}r\\[5pt]
r_{0.025}&=\text{tanh}(Z_{0.025})\\[5pt]
&=\text{tanh}(0.477)\\[5pt]
&=0.444\end{aligned}$$
よって、標本相関係数\(r=0.6\)が棄却限界値\(r_{0.025}=0.444\)より大きいため、サンプル数\(N=20\)の標本相関係数\(r=0.6\)は有意とわかりました。
ちなみに、母集団の相関係数\(\rho=0\)のとき、標本相関係数が\(r=0.6\)以上となる確率は下記となります。
$$\begin{aligned}Z&=\text{tanh}^{-1}r\\[5pt]
&=\frac{1}{2}\text{ln}\frac{1+r}{1-r}\\[5pt]
&=\frac{1}{2}\text{ln}\frac{1+0.6}{1-0.6}\\[5pt]
&=0.693\end{aligned}$$
標準正規分布に直して、標準正規分布表を用いると、
$$P(z>\frac{0.693-0}{0.234})=P(z>2.85)\approx 0.002$$
よって、上側確率0.025よりも小さいので、標本相関係数\(r=0.6\)が有意であることがわかります。
95%信頼区間に基づくサンプルサイズの決め方
上記の例題では、サンプル数\(N=20\)、母集団の相関係数\(\rho=0\)のときの棄却限界値を求めました。
同様に、サンプル数\(N\)と母集団の相関係数\(\rho\)を様々に変更し、棄却限界値を求めると下図の結果が得られます。

必要なサンプルサイズの求め方
①サンプルサイズ\(N\)を決める。
②母集団相関係数\(\rho\)を[-1,1]の範囲で指定する。
③(5),(6)式を用いて、平均\(\mu_Z\)と標準誤差\(\sigma_Z\)を求める。
④(11)式を用いて、有意水準\(\alpha=0.05\)(両側検定)でのフィッシャーのz変換の棄却限界値\(Z_{0.025},Z_{0.975}\)を求める。
⑤フィッシャーのz変換より、標本相関係数\(r\)の棄却限界値\(r_{0.025},r_{0.975}\)を求める。
検定力分析によるサンプルサイズの決め方
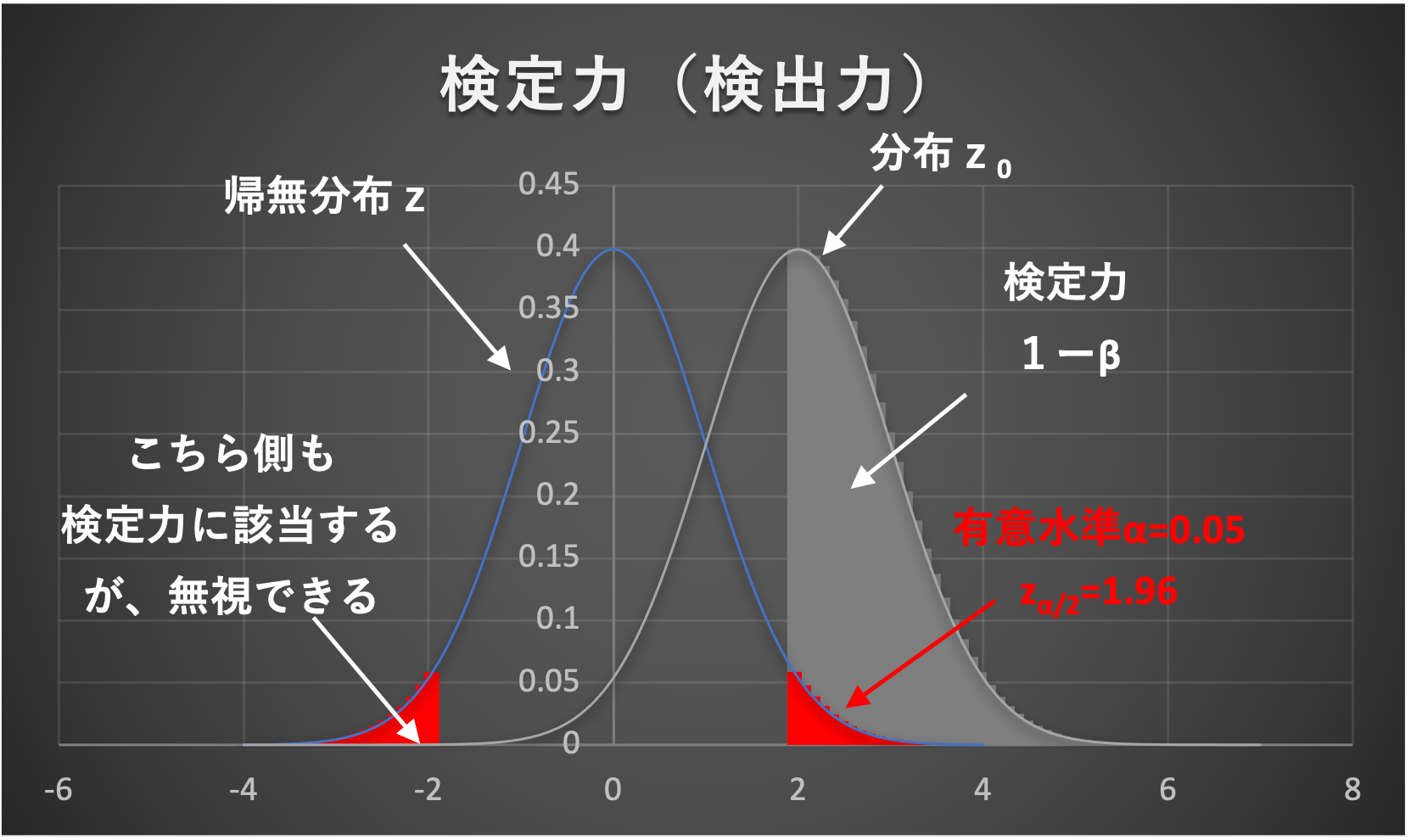
検定力とは、母集団において"無相関でない"場合に、ちゃんと有意な相関が得られる確率のことです。
母集団の相関関係を正しく"検出できる"確率という意味で、検出力とも呼ばれます。
母集団の相関係数が、いくら程度ならば正しく検出する必要があるのかを考えて、検定力が十分高くなるようにサンプルサイズを決めていきます。
ネイマン=ピアソン理論によると、検定力(検出力)の立ち位置は下表の通りです。
| 事実 | 帰無仮説を採択 | 帰無仮説を棄却 |
| 帰無仮説が真(無相関) | 正しい判断 \(1-\alpha\) |
第1種の誤り 有意水準\(\alpha\) |
| 帰無仮説が偽(相関あり) | 第2種の誤り \(\beta\) |
正しい判断 検定力\((1-\beta)\) |
有意水準\(\alpha\)は小さければ良いというものではなく、検定力\(1-\beta\)も同時に小さくなってしまいます💦

それでは、検定力を求めてみましょう。
検定力(検出力)の求め方
①サンプルサイズ\(N\)と母集団相関係数\(\rho\)を決める。
②(5),(6)式を用いて、平均\(\mu_Z\)と標準誤差\(\sigma_Z\)を求める。
⇒フィッシャーのz変換値は、正規分布\(N(\mu_Z,\sigma_Z^2)\)に従う。
③母集団が無相関\(\rho=0\)のときの、フィッシャーのz変換の棄却限界値\(Z_{0.025},Z_{0.975}\)を求める。
※有意水準\(\alpha=0.05\)(両側検定)とする
④ ②で求めた平均\(\mu_Z\)と標準誤差\(\sigma_Z\)を用いて\(Z_{0.025},Z_{0.975}\)を標準化し、\(z_{0.025},z_{0.975}\)を求める。
⑤標準正規分布表を用いて、検定力(検出力)\(1-\beta\)を求める。
$$P(z>z_{0.025})$$
$$P(z<z_{0.975})$$
$$1-\beta = P(z>z_{0.025})+P(z<z_{0.975})$$
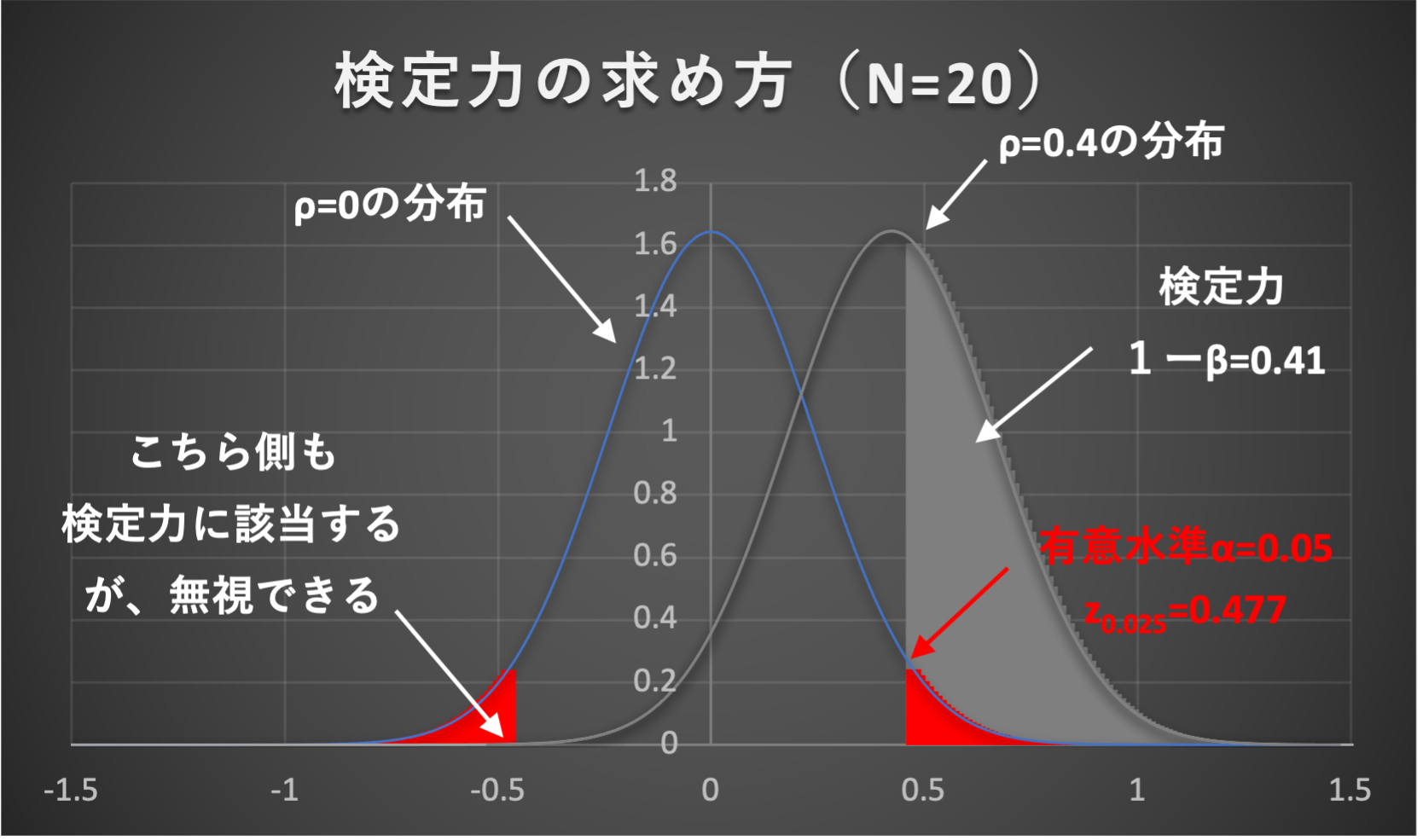
それでは、これまでの例題と同様、サンプル数\(N=20\)、帰無仮説\(H_0:\rho = 0\)、有意水準\(\alpha=0.05\)(両側検定)の場合を考えましょう。
ここで、実際の母集団相関係数が\(\rho=0.4\)だったとします。
(5),(6)式を用いて、平均\(\mu_Z\)と標準誤差\(\sigma_Z\)を求めます。
$$\begin{aligned}\mu_Z &= \frac{1}{2}\text{ln}\frac{1+\rho}{1-\rho}\\[5pt]
&=\frac{1}{2}\text{ln}\frac{1+0.4}{1-0.4}\\[5pt]
&=0.424\end{aligned}$$
$$\begin{aligned}\sigma_Z&=\frac{1}{\sqrt{N-3}}\\[5pt]
&=\frac{1}{\sqrt{20-3}}\\[5pt]
&=0.243\end{aligned}$$
次に、母集団が無相関\(\rho=0\)のときの、フィッシャーのz変換の棄却限界値\(Z_{0.025},Z_{0.975}\)を求めます。
母集団が無相関\(\rho=0\)のとき、平均\(\mu_Z=0\)と標準誤差\(\sigma_Z=0.243\)であるので、
$$\begin{aligned}\frac{Z_{0.025}-0}{0.243}&=1.96\\[5pt]
Z_{0.025}&=1.96\times0.243\\[5pt]
&=0.477\end{aligned}$$
$$\begin{aligned}\frac{Z_{0.975}-0}{0.243}&=-1.96\\[5pt]
Z_{0.975}&=-1.96\times0.243\\[5pt]
&=-0.477\end{aligned}$$
よって、母集団相関係数が\(\rho=0.4\)のときの平均\(\mu_Z=0.424\)と標準誤差\(\sigma_Z=0.243\)を用いて\(Z_{0.025},Z_{0.975}\)を標準化すると、
$$\begin{aligned}z_{0.025}&=\frac{Z_{0.025}-0.424}{0.243}\\[5pt]
&=\frac{0.477-0.424}{0.243}\\[5pt]
&=0.218\end{aligned}$$
$$\begin{aligned}z_{0.975}&=\frac{Z_{0.975}-0.424}{0.243}\\[5pt]
&=\frac{-0.477-0.424}{0.243}\\[5pt]
&=-3.71\end{aligned}$$
標準正規分布表を用いると、
$$P(z>0.218)\approx0.41$$
$$P(z<-3.71)\approx0$$
したがって、検定力(検出力)\(1-\beta\)は、下記のように求まります。
$$\begin{aligned}1-\beta &= P(z<-3.71)+P(z>0.218)\\[5pt]
&=0.41\end{aligned}$$
以上の計算を図示してみると下図のようになります。
上記と同様に、サンプル数\(N\)と母集団の相関係数\(\rho\)を様々に変更し、検出力を求めると下図の結果が得られます。

参考文献
1.心理統計学の基礎(有斐閣アルマ)統計検定2級〜準1級レベル
本記事では、この本を大いに参考にさせてもらいました。
サンプルサイズについて詳しく、かつわかりやすく解説してくれています。
無相関検定を"詳しく"解説している教科書は他に見つかりませんでした。
-

-
【書評】心理統計学の基礎 難易度と読み方を解説!
続きを見る
無相関検定やサンプルサイズの求め方について解説されています。
やさしい教科書の部類ですが、検定力分析については詳しく書かれており実践的です。

