
現場で使われている「外れ値の検出方法」が知りたいな。
こんなお悩みを解決します。
どうも。こんにちは。
ケミカルエンジニアのこーしです。
本日は、データ分析における「外れ値の検出方法」についてわかりやすく解説します。
外れ値を含んだデータをそのまま分析したり、見た目で外れ値を判断したりすると、誤った分析結果が得られることがあります。
間違った判断をしないよう、現場でよく使われている「外れ値の検出方法」についてしっかり学んでいきましょう!
本記事の内容
- 外れ値検出の流れ
- 生データの可視化
- 統計量(平均値、標準偏差、中央値、最小値、最大値)の確認
- 外れ値の検出
- 外れ値の解釈
- 加工データの可視化
- 参考文献
この記事を書いた人
 こーし(@mimikousi)
こーし(@mimikousi)
目次
外れ値検出の流れ
データ分析における外れ値の検出は下記のような流れで行います。
外れ値検出の流れ
- 生データの可視化
- 統計量(平均値、標準偏差、中央値、最小値、最大値)の確認
- 外れ値の検出
- 外れ値の解釈
- 外れ値の除去
- 加工データの可視化
外れ値を除去するまでに、意外と多くの手順を踏む必要があります。
特に、グラフで可視化して確認する作業は省いてはいけません。
生データの可視化
まず最初に、"目視"でデータセットを確認してみましょう。
じっくりと生データを見て、データの全体像を頭に叩き込みましょう!
見るべきポイント
- データのサイズ感
- データの値(桁数)
- 外れ値や欠測値の有無・多少
- データの特徴
そして次に、生データを「可視化」しましょう。
可視化するため、下記2つのグラフを作成します。
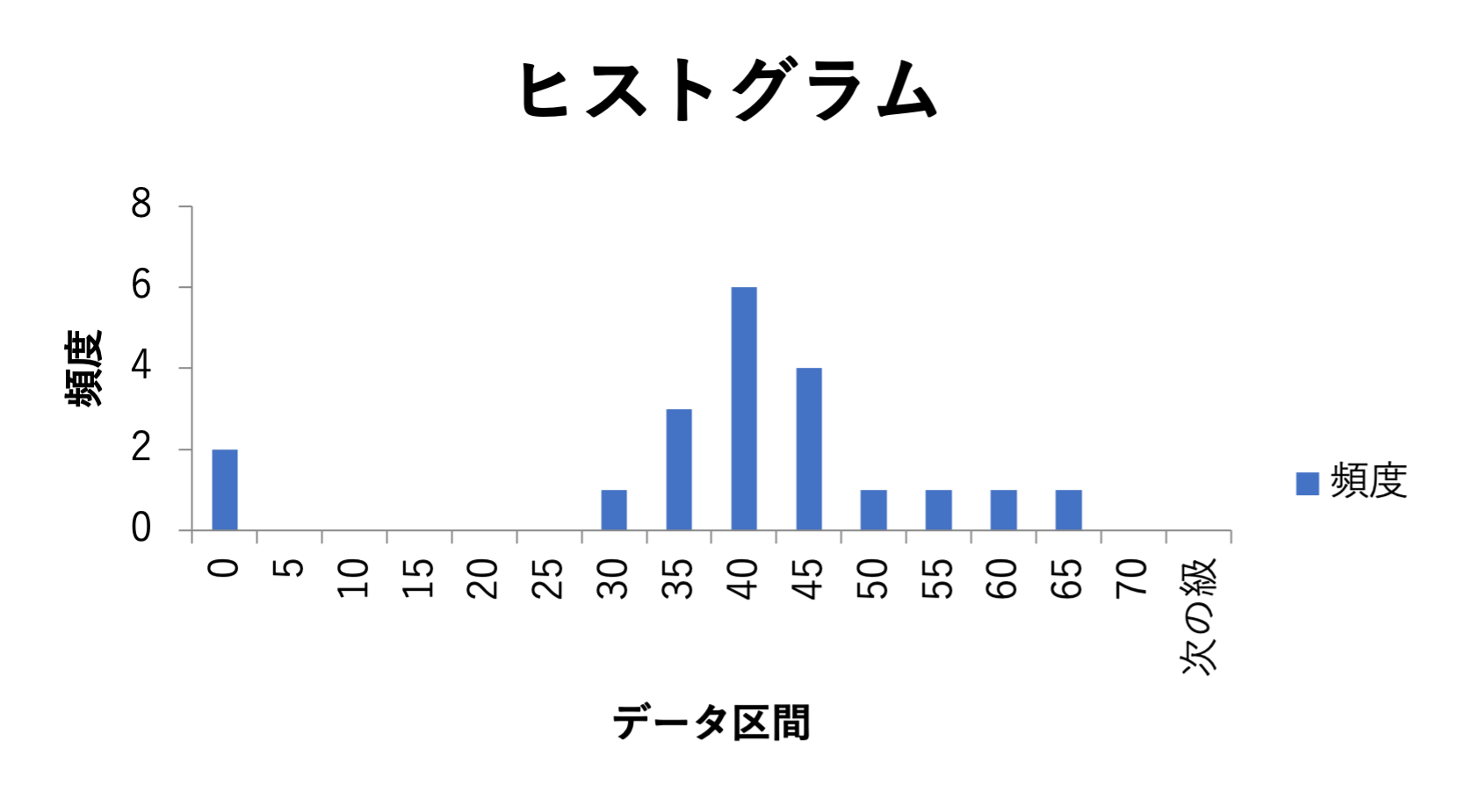
1)ヒストグラム
1変数の分布の形を知ることができます。
2)散布図
2変数の関係を知ることができます。
散布図の描き方は一般的だと思うので、本記事ではヒストグラムをエクセルで描く方法を簡単に紹介します。
生データの例
下表の生データを例にして解説していきます。
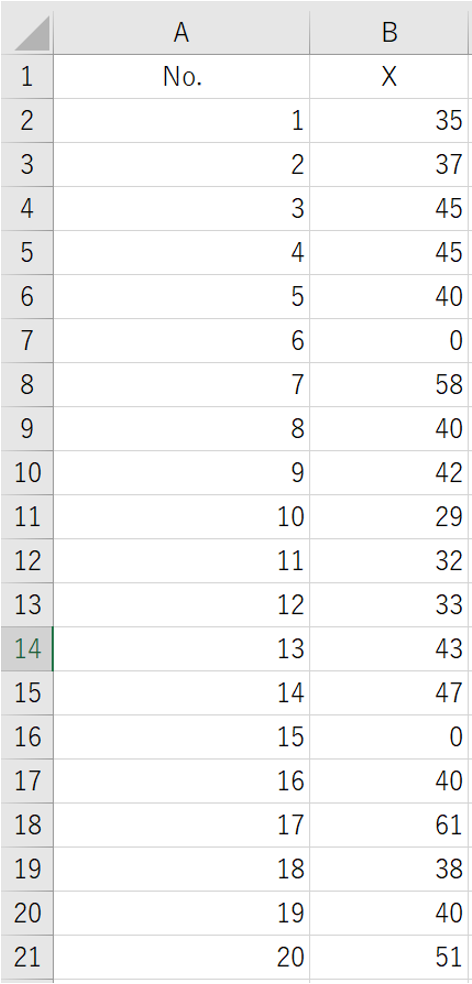
ヒストグラムの描き方
 エクセルでヒストグラムを書くためには、アドインの「分析ツール」を使いましょう。
エクセルでヒストグラムを書くためには、アドインの「分析ツール」を使いましょう。
アドインを使わないやり方もありますが、アドインを使った方が簡単です。
1.アドイン「分析ツール」のインストール
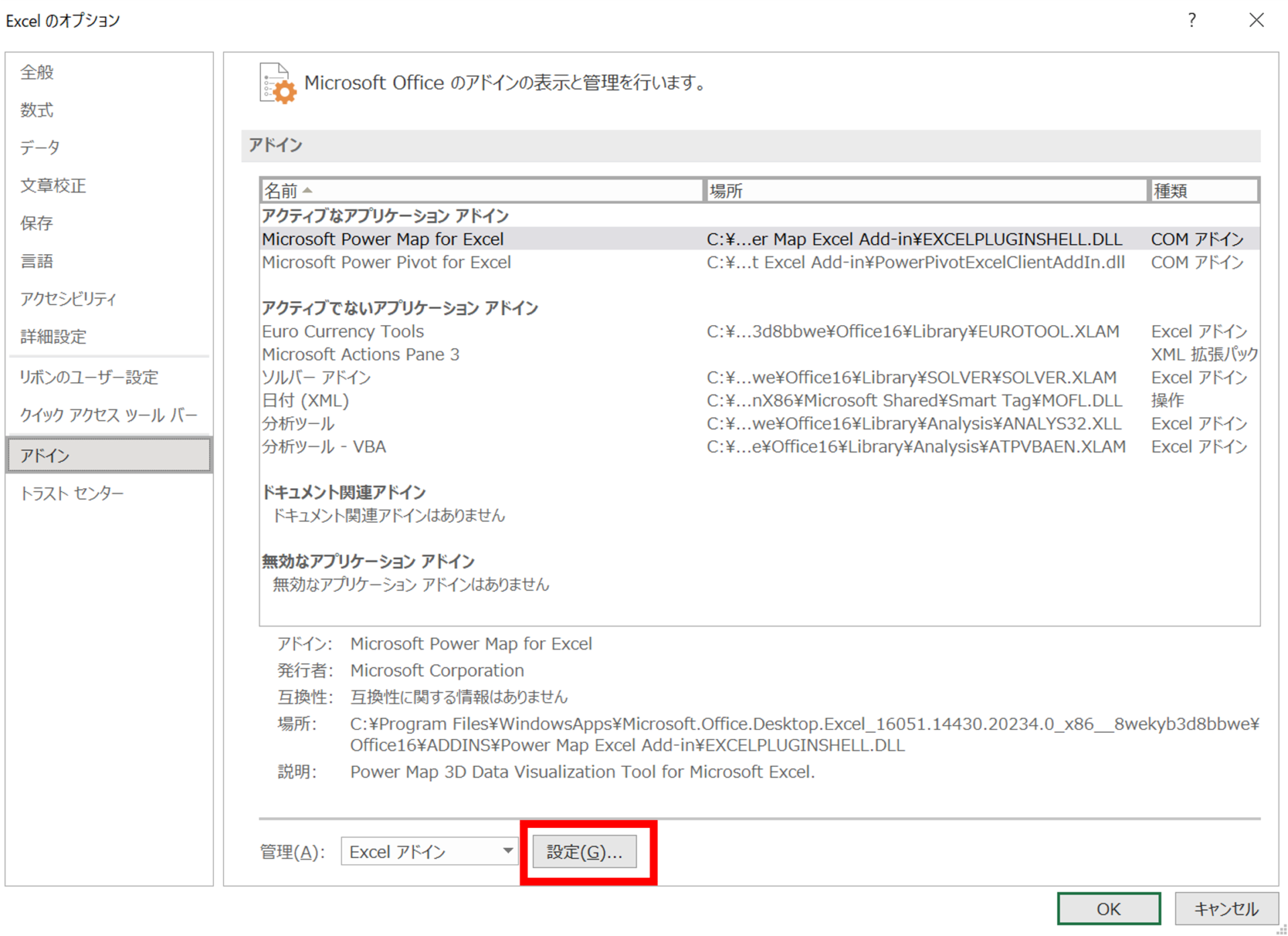
1)[ファイル]⇒[オプション]⇒[アドイン]⇒[設定]
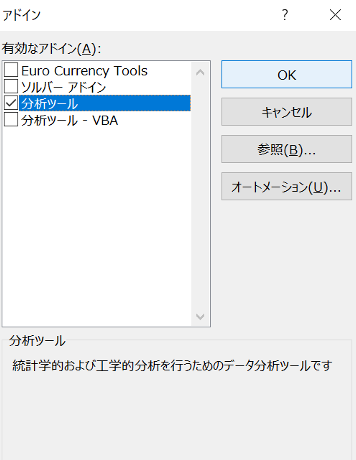
2)「有効なアドイン」の中から「分析ツール」にチェックを入れて「OK」を押す
2.「データ分析」を使う
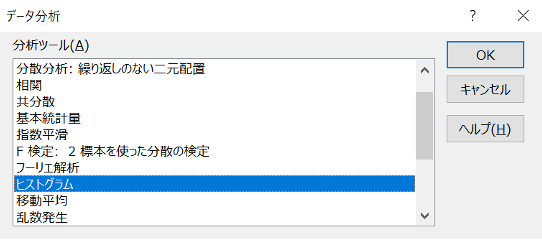
1)[データ]タブにある「データ分析」をクリックする
2)「ヒストグラム」を選択して、「OK」を押す
3.ヒストグラムを描く
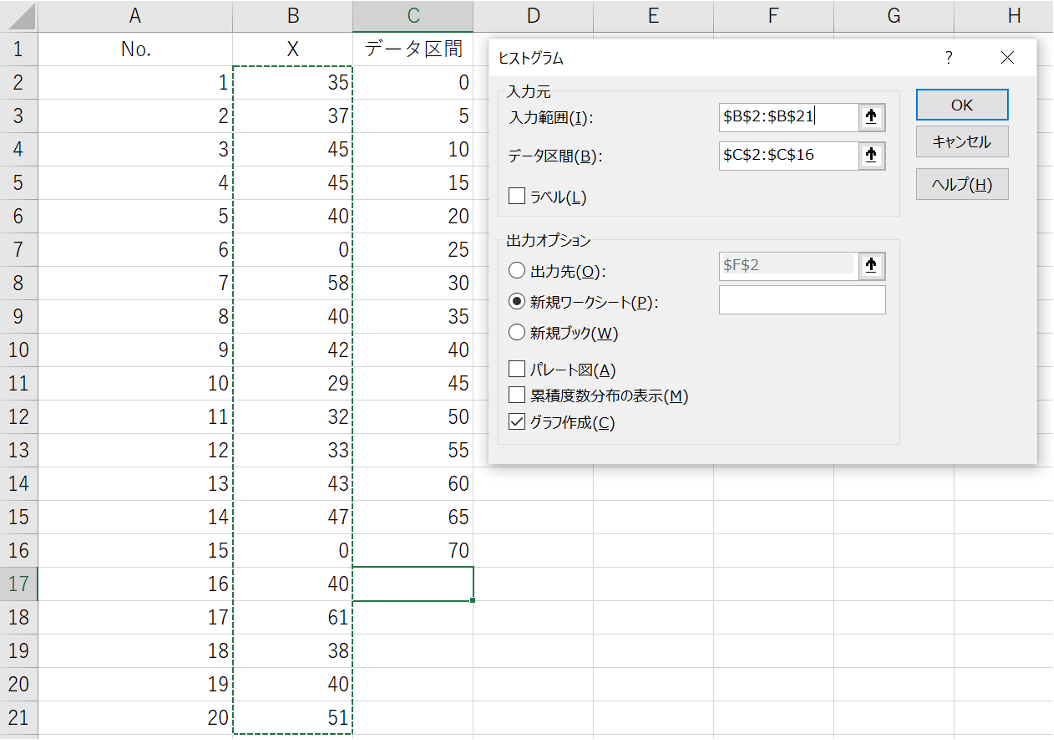
1)[入力範囲]を選択する
使用したいデータ範囲を選択します。
2)[データ区間]を選択する
横軸の刻み幅(ビンの幅)をどのくらいしたいのかを指定します。
3)[新規ワークシート]にチェックを入れる
同じシートに出力したい場合は、[出力先]にチェックを入れ、出力したいセルを入力します。
4)[グラフ作成]にチェックを入れる
他にもパレート図や累積度数分布が必要な場合は、チェックを入れます。
5)「OK」を押す

以上、簡単にヒストグラムの描き方を説明しましたが、詳しく知りたい方は下記リンクを参考にしてみてください。
統計量(平均値、標準偏差、中央値、最小値、最大値)の確認
エクセルでデータセットの各統計量を計算してみます。
| 統計量 | 関数 |
| 平均値 | =AVERAGE(開始セル:終了セル) |
| 標準偏差 | =STDEV.S(開始セル:終了セル) |
| 中央値 | =MEDIAN(開始セル:終了セル) |
| 最小値 | =MIN(開始セル:終了セル) |
| 最大値 | =MAX(開始セル:終了セル) |
| 合計 | =SUM(開始セル:終了セル) |
| データ個数(数値データ) | =COUNT(開始セル:終了セル) |
| データ個数(空白以外) | =COUNTA(開始セル:終了セル) |
計算が多くて大変ですが、一つ一つしっかりと計算しましょう!
上で示した「生データの例」を用いて計算してみた結果は、下図の通りです。
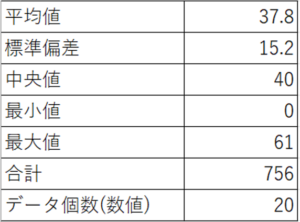
外れ値の検出
3シグマ法
外れ値の検出によく使われているのが、「3シグマ法」です。
シグマ(σ)は標準偏差であり、分布のばらつきを表しています。
データが正規分布に従う場合、管理基準を「平均値(μ)±3σ」とすると、管理基準を超える確率は0.3%程度となります。
よって、管理基準を超えた場合は、異常が発生したと判断することができます。
ちなみに、平均値、標準偏差の計算式は下記の通りです。
$$\mu = \frac{\sum\limits_{i=1}^nx_{i}}{n}$$
$$\sigma = \sqrt{\frac{\sum\limits_{i=1}^n(x_{i}-\mu)^2}{n-1}}$$
ここで、上限管理限界(Upper Control Limit;UCL)と下限管理限界(Lower Control Limit;LCL)は、下記のように書けます。
$$\text{UCL} = \mu + 3\sigma$$
$$\text{LCL} = \mu - 3\sigma$$
データがUCL、LCLを超えた場合、そのデータは外れ値と見なされます。
上の「生データの例」で計算してみると、下記となります。
$$\begin{aligned}\text{UCL} &= 37.8+3\times15.2\\[5pt]
&=83.3\end{aligned}$$
$$\begin{aligned}\text{LCL} &= 37.8 - 3\times15.2\\[5pt]
&=-7.7\end{aligned}$$
計算してみると、UCLは最大値61よりも大きく、LCLも最小値0より小さくなり、外れ値は存在しないという結果となりました。
元のデータに外れ値が含まれていると、平均値は真値からズレ、標準偏差も過大に計算されてしまうため、3シグマ法では外れ値を正しく検出できないということがわかります。
よって、外れ値の検出には「四分位偏差法」や「Hampel Identifier」を使うのが適切です。
「四分位偏差法」や「Hampel Identifier」では、平均値ではなく「中央値」を使います。
四分位偏差法(箱ひげ図)
よく使われる外れ値の検出方法の一つに「四分位偏差法」があります。
箱ひげ図においては、四分位偏差法を用いて外れ値を検出します。
四分位偏差法で用いる用語を下表にまとめました。
| 名称 | 記号 | 内容 |
| 最小値 | Q0 | 小さい方から数えて0%のデータ |
| 第1四分位数 | Q1 | 小さい方から数えて25%のデータ |
| 第2四分位数 (中央値) |
Q2 | 小さい方から数えて50%のデータ |
| 第3四分位数 | Q3 | 小さい方から数えて75%のデータ |
| 最大値 | Q4 | 小さい方から数えて100%のデータ |
| 四分位範囲 | IQR | =第3四分位数 ー 第1四分位数 =(Q3-Q1) |
| 四分位偏差 | QD | =(第3四分位数 ー 第1四分位数)/ 2 =(Q3-Q1)/2 |
四分位偏差法におけるUCL(上限管理限界)は「第3四分位数+3×四分位偏差」であり、LCL(下限管理限界)は「第1四分位数ー3×四分位偏差」となります。
$$\text{UCL} = \text{Q3} + 3\text{QD}$$
$$\text{LCL} = \text{Q1} - 3\text{QD}$$
多くの教科書では、箱ひげ図の外れ値は「四分位範囲」を用いて解説されています。
意味は同じですが、3シグマ法と比較するため本記事では「四分位偏差」を使用しています。
ちなみに、「四分位範囲」を用いてUCLとLCLを表すと下記のようになります。
$$\text{UCL} = \text{Q3} + 1.5\text{IQR}$$
$$\text{LCL} = \text{Q1} - 1.5\text{IQR}$$
四分位偏差や四分位範囲がよくわからない方は下記リンクを参考にしてください。
エクセル関数の紹介
四分位数や四分位偏差などは、エクセル関数を使って求めることができます。
=QUARTILE.INC(開始セル:終了セル, 引数)
引数は、下表を参考に指定します。
| 引数 | 名称 |
| 0 | 最小値 |
| 1 | 第1四分位数 |
| 2 | 第2四分位数 |
| 3 | 第3四分位数 |
| 4 | 最大値 |
それでは、エクセル関数を使って「生データの例」を計算してみましょう。
結果は下図の通りです。
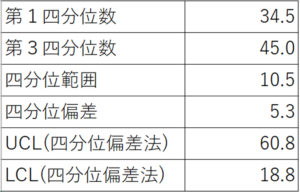
また、UCLやLCLは下記の通り計算しました。
$$\begin{aligned}\text{UCL} &= 45+3\times5.3\\[5pt]
&=60.8\end{aligned}$$
$$\begin{aligned}\text{LCL} &= 34.5 - 3\times5.3\\[5pt]
&=18.8\end{aligned}$$
よって、外れ値は下図の通り検出できました。
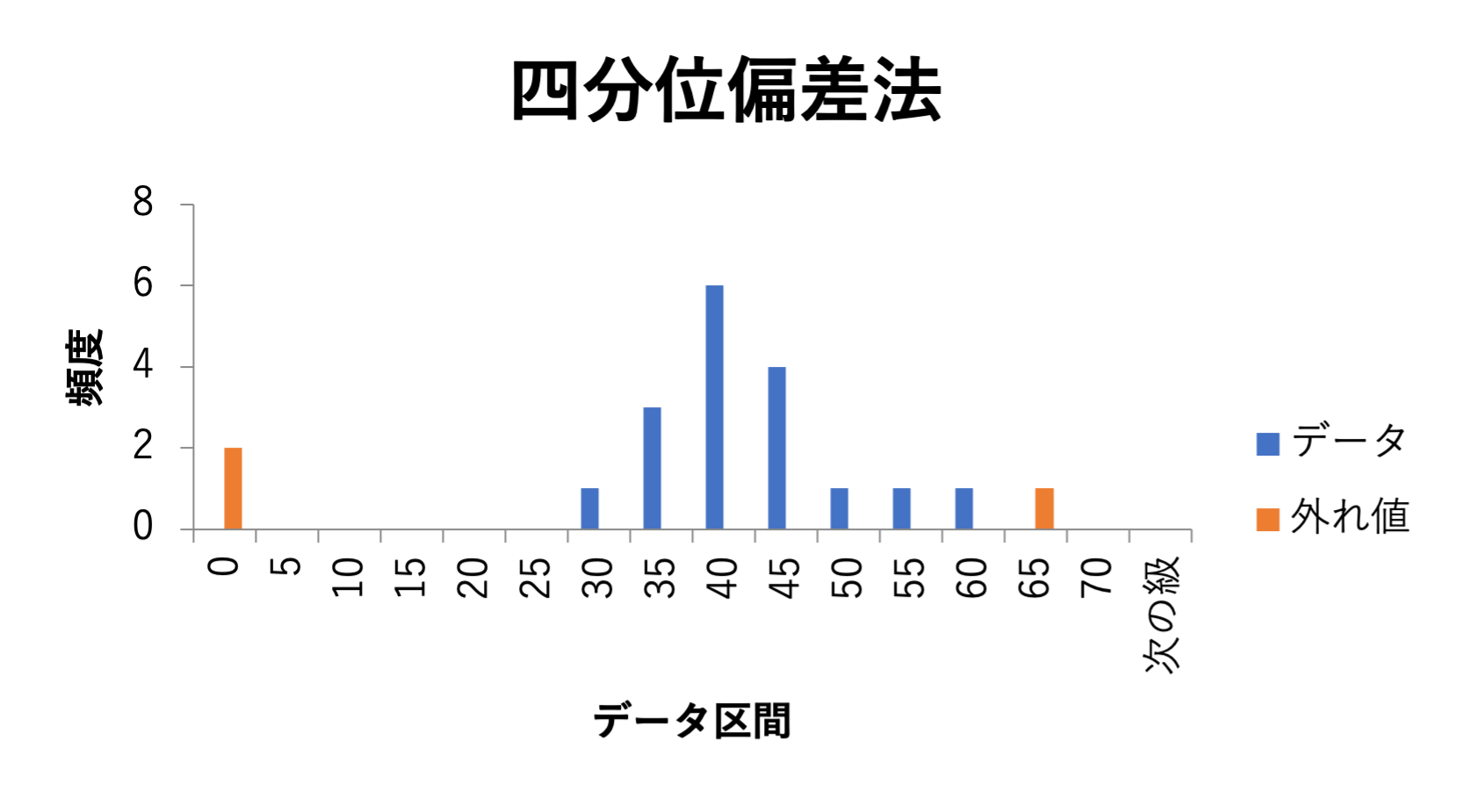
【参考記事】
Hampel Identifier
ソフトセンサーの教科書では、「Hampel Identifier」が推奨されています。
Hampel Identifierは、3シグマ法を中央値ベースに変更したものです。
平均値 ⇒ 中央値(median)
標準偏差 ⇒ 中央絶対偏差(Median Absolute Deviation;MAD)
$$\text{MAD} = 1.4826\text{median}(|x -\text{median}(x)|)$$
「変数xと中央値の差」の絶対値を計算し、それらの中央値に1.4826を掛けたものが、中央絶対偏差(MAD)となります。

よって、管理限界は下記のようになります。
$$\text{UCL} = \text{median}(x) + 3\text{MAD}$$
$$\text{LCL} = \text{median}(x) - 3\text{MAD}$$
上の「生データの例」で計算してみると、\(\text{MAD}=7.4\)となるので、UCL、LCLは下記となります。
$$\begin{aligned}\text{UCL} &= 40+3\times7.4\\[5pt]
&=62.2\end{aligned}$$
$$\begin{aligned}\text{LCL} &= 40- 3\times7.4\\[5pt]
&=17.8\end{aligned}$$
よって、外れ値は下図の通り検出できました。
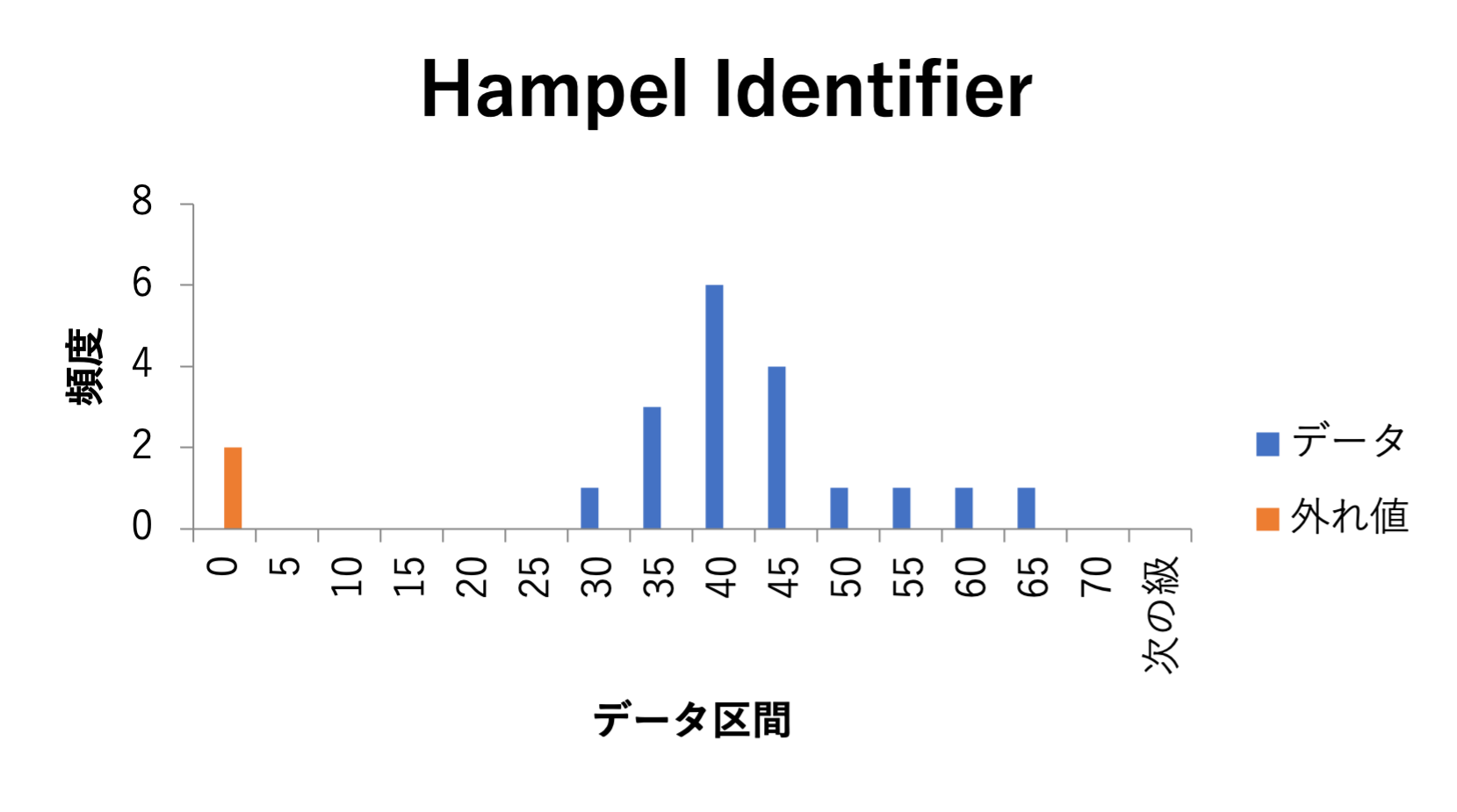
Moving Hampel
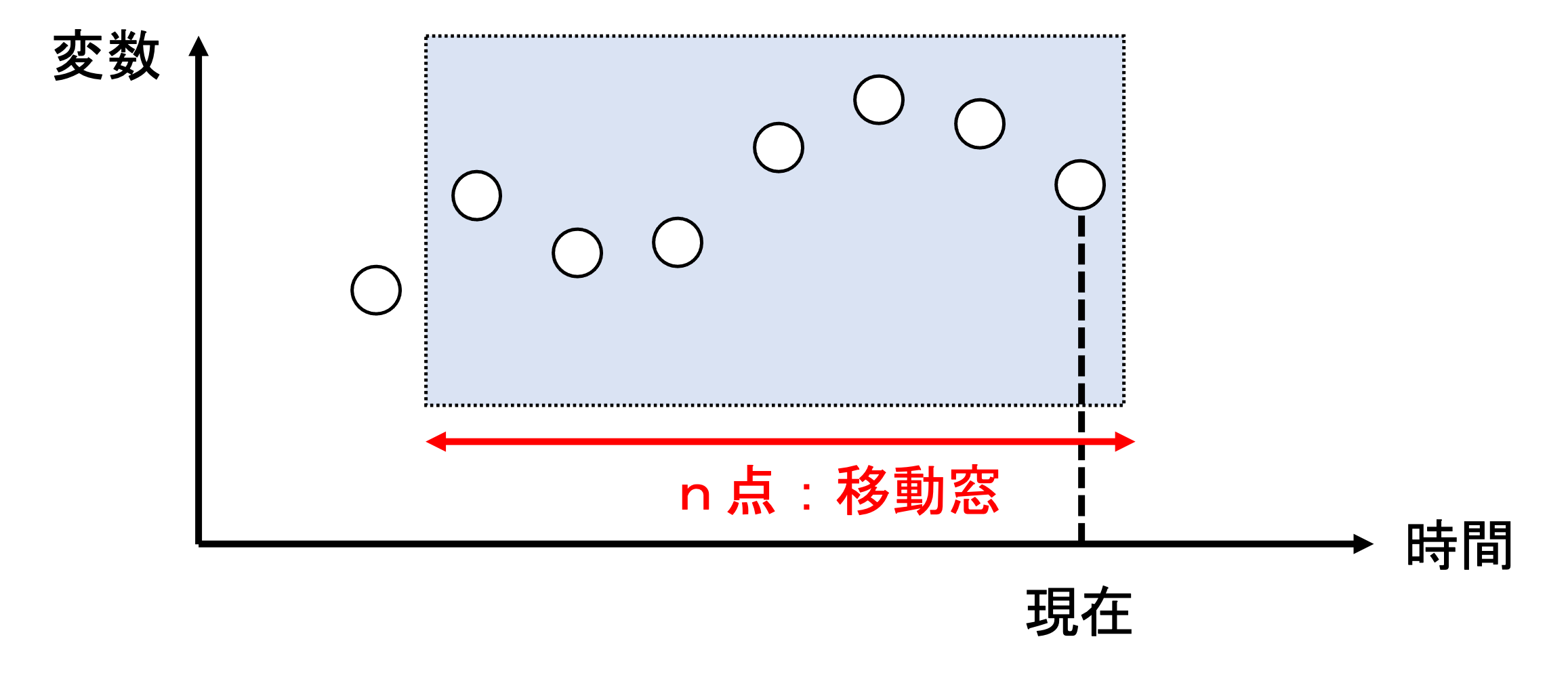
データが中央値を中心にランダムにバラついている場合、データ全体にHampel Identifierを適用することで、外れ値を検出することができます。
一方、時系列データのように、変数が非定常に変化している場合は、うまく外れ値を検出することができません。
そこで、移動窓(Moving Window)を利用し、現時刻を含めて過去n点のデータで繰り返しHampel Identifierを行うことで、外れ値を検出します。
この方法を「Moving Hampel」と呼びます。
その他、主成分分析を用いた多変数の外れ値検出もありますが、本記事では割愛します。
外れ値の解釈
上記手法によって外れ値を検出した後は「外れ値の解釈」を行います。
つまり、「本当に外れ値と見なして良いのか」を判断します。
判断の手順
1.外れている理由を調査する
2.外れている理由を想像する
3.外れ値を除いて分析してみる
外れ値に何らかの理由が隠されている場合、外れ値を除くと分析結果に誤りが生じます。
よって、なぜ「外れ値」となったのか、調べる必要があります。
除去してはいけない重要なデータを「外れ値」と判断し、意思決定を誤った事例は多々あります。
「本当に除去して良いのか?」よく考えてから外れ値を除去しましょう!

加工データの可視化
最後に、外れ値を除去した加工データを再び可視化します。
1)ヒストグラム
2)散布図
そして、生データを可視化した先ほどのグラフと比較してみましょう。
外れ値を除去したことで、どんな変化が生まれているのか、要チェックです!

参考文献
1.仮想計測技術の開発 ,計測と制御,第51巻(2012)9号
京都大学加納先生の記事です。
加納先生は、noteでブログも書かれています。
ソフトセンサーの教科書といえば、この本しか思いつきません。
東京大学の船津先生と金子先生(現明治大学)が書かれています。
統計学の用語がバシバシ出てくるので、ある程度統計学を勉強してから読むべきですね。
外れ値検出の流れを参考にさせてもらいました。
実務でひっかかるところを非常にわかりやすく解説してくれてます。
基礎的なところから優しく解説してくれているので、初心者向けですね。
