どうも、こんにちは。ケミカルエンジニアのこーしです。
本日は、ポンプの全揚程の計算方法について、わかりやすく解説していきたいと思います。
この記事を読むことで、ポンプの設計に必要な全揚程を計算できるようになります。
また、稼働しているポンプの現状能力も確認できるようになります。
本記事の内容
・ポンプの全揚程とは
・全揚程の求め方
・現場で使える全揚程の計算例
この記事を書いた人
こーし(@mimikousi)
目次
ポンプの全揚程とは？
はじめてポンプの性能曲線を見たときは、「全揚程って何だ？」と思いますよね。 全揚程の定義は下記のとおりです。
全揚程とは、ポンプによって流体が得た全エネルギー（ヘッド）のこと
全揚程を分解して表すと、下記の関係となります。
全揚程(m) ＝ A 速度ヘッド差 ＋ B 位置ヘッド差 ＋ C 圧力ヘッド差 ＋ D 損失ヘッド
A 速度ヘッド差
吸込側と吐出側の運動エネルギー（ヘッド）の差を表します。
吸込側と吐出側で配管径が同じ場合は無視できます。
仮に配管径が異なる場合でも、速度ヘッド差は、位置ヘッド差（実揚程）や圧力ヘッド差に比べて十分小さいため、無視して大丈夫です。
B 位置ヘッド差
吸込側と吐出側の高さの差を表しており、一般に「実揚程」と呼ばれています。
C 圧力ヘッド差
吸込圧力（ヘッド）と吐出圧力（ヘッド）の差を表します。
圧力ヘッド差 ＝ 吐出圧力ヘッド ー 吸込圧力ヘッド で表せるため、全揚程と吐出圧力が異なることがわかります。
D 損失ヘッド
配管や熱交換器、バルブなどによるエネルギー（ヘッド）損失を表します。
一般に「圧損」と呼ばれるものです。 圧損もヘッドの形で表すことでができます。
ポンプの性能曲線
モノタロウ 遠心ポンプの基礎講座 3-1ポンプの性能曲線の見方より引用
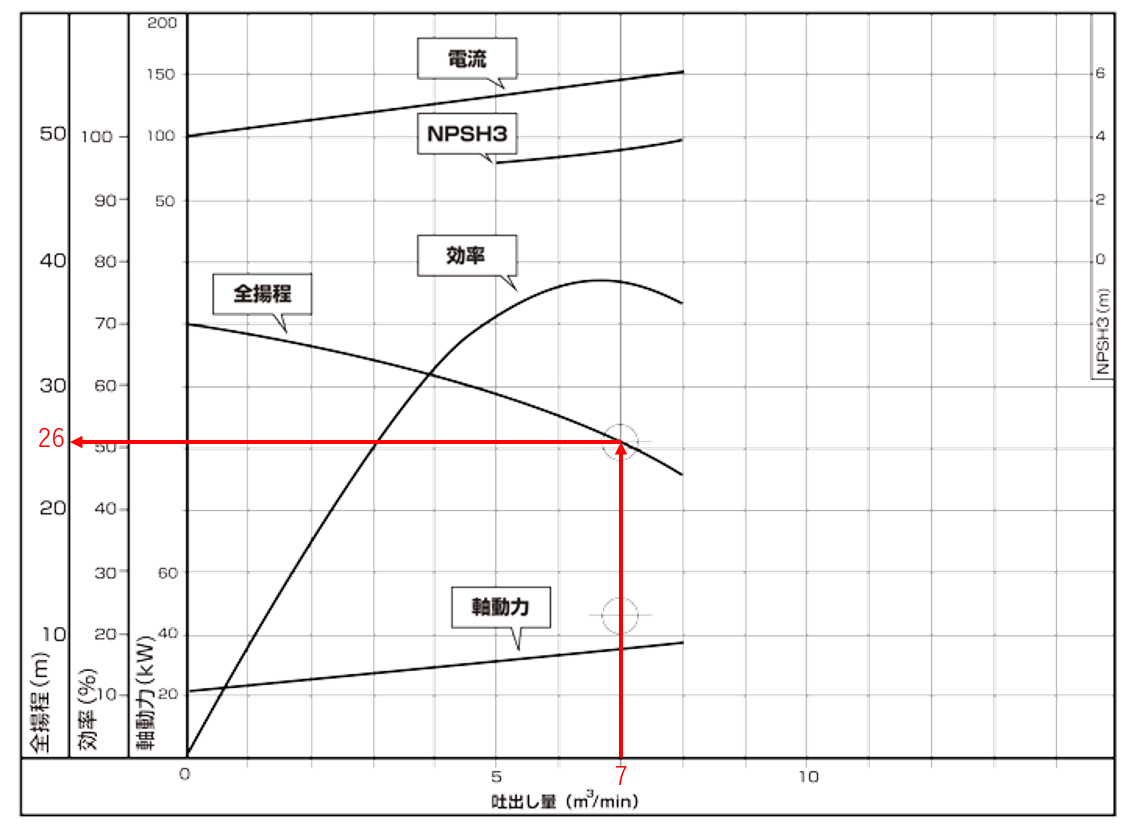
まず、ポンプの性能曲線を見てみましょう。
横軸が、吐出し量[m3/min] 縦軸が、全揚程[m] です。
例えば、吐出し量が7 m3/minのとき、全揚程は、26 mであることがわかります。
＜＜NPSHとは？＞＞
続きを見る
参考【解説】ポンプのキャビテーション対策（ＮＰＳＨとは？）
＜＜ポンプの性能曲線の見方＞＞
続きを見る
参考【解説】ポンプの性能曲線の見方
流体のエネルギー収支式
流体のエネルギー収支式を考えてみましょう。
エネルギー収支をとると下記のような関係になります。
運動エネルギー ＋ 位置エネルギー ＋ 圧力エネルギー = 一定
数式で表してみると、ベルヌイの式と呼ばれる下記（１）式となります。
ベルヌイ（Bernoulli）の式
\(u\) : 流体の速度 [m/s] \(\rho\): 流体の密度 [kg/m³] ※非圧縮性流体とする（例：水） \(g\) : 重力加速度 [m/s²] \(h\) : 高さ [m] \(p\) : 圧力 [Pa]
（１）式の各項の単位は、圧力（Pa）となり、圧力収支式の形となっています。
第１項は「動圧」と呼ばれ、第３項は「静圧」と呼ばれます。
動圧と静圧を合わせて「全圧」と呼ばれます。
ここで、（１）式の両辺を流体の密度\(\rho\)で割ると、（２）式が得られます。
（２）式の各項の単位は、単位質量あたりのエネルギー（J/kg)となり、エネルギー収支式の形となっています。
同様に、（２）式の両辺をさらに重力加速度\(g\)で割ると、（３）式が得られます。
（３）式の各項の単位は、長さ（m）となり、ヘッドの収支式の形になりました。
（３）式の各項は、下記のように呼ばれます。
$$\textbf{速度ヘッド}\ \ \ \frac {u^{2}}{2g}$$$$\textbf{位置ヘッド}\ \ \ {h}$$$$\textbf{圧力ヘッド}\ \ \ \frac {p}{\rho g}$$
ポンプの全揚程の式
ここで、下記２点を考慮すると、（３）式は（４）式のように書くことができます。
①ポンプの全揚程 \(H\) [m]
②配管や熱交換器、バルブなどによるエネルギー損失ヘッド
\(\Sigma F=\frac {\Sigma \Delta P}{\rho g}\) [m] （配管や熱交換器、バルブなどによる圧力損失の総和を\(\Sigma \Delta P\)とする）
機械的エネルギー収支式
\(u\) : 流体の速度 [m/s] \(\rho\): 流体の密度 [kg/m³] ※非圧縮性流体とする（例：水） \(g\) : 重力加速度 [m/s²] \(h\) : 高さ [m] \(p\) : 圧力 [Pa] \(H\) : 全揚程 [m] \(\Sigma F\) : 損失ヘッド [m] 添字1 : ポンプの吸込側 添字2 : ポンプの吐出側
よって、全揚程は（５）式のように表せます。
ポンプの全揚程の式
$$\textbf{速度ヘッド差}\ \ \ \frac {u^{2}_{2}-u^{2}_{1}}{2g}$$$$\textbf{位置ヘッド差}\ \ \ {h_{2}-h_{1}}$$$$\textbf{圧力ヘッド差}\ \ \ \frac {p_{2}-p_{1}}{\rho g}$$$$\textbf{損失ヘッド}\ \ \ \Sigma F$$
したがって、ポンプの全揚程の式は、冒頭に示した下記の関係になることが確認できました。
全揚程(m) ＝ 速度ヘッド差 ＋ 位置ヘッド差 ＋ 圧力ヘッド差 ＋ 損失ヘッド
ポンプの全揚程 計算例
計算例１ 全揚程の算出（吸込側に圧力計がある場合）
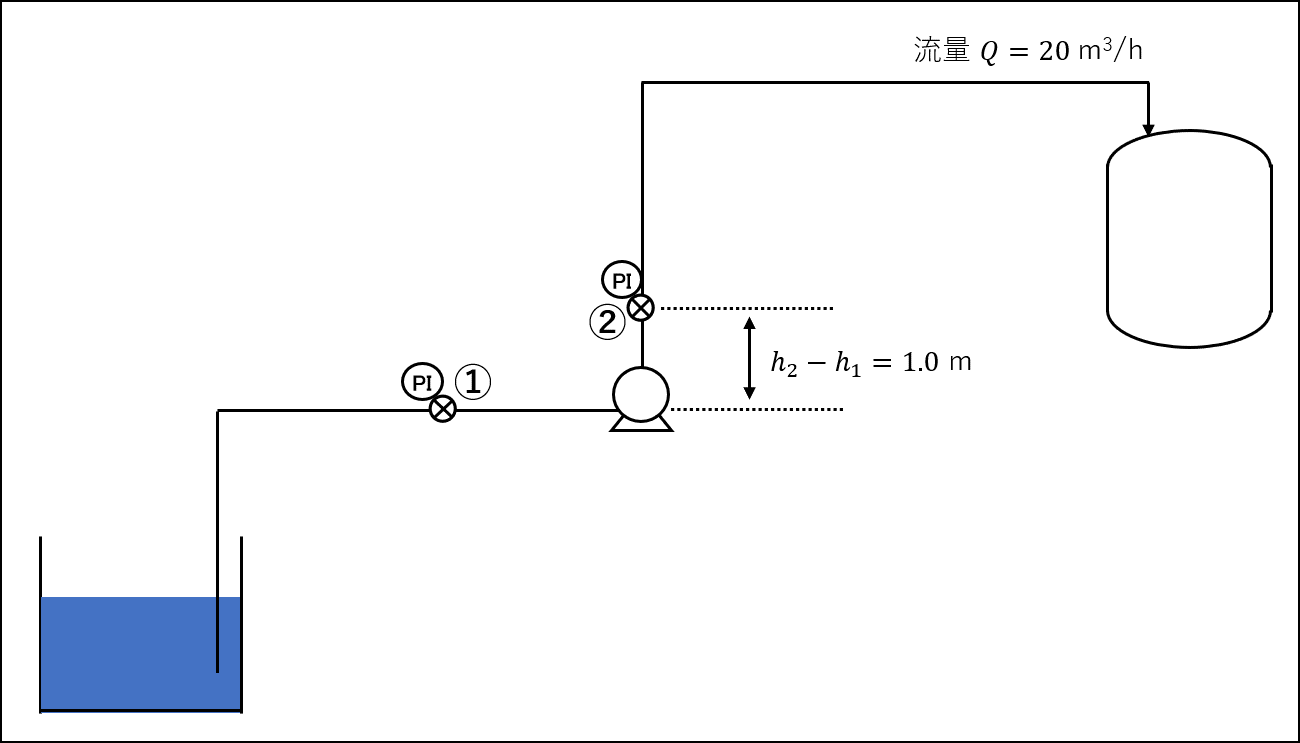
まず、吸込側に圧力計がある場合について、ポンプの全揚程を計算してみましょう。
吸込圧力計の位置を①、吐出圧力計の位置を②として、これらの点①ー②間でエネルギー収支をとると、全揚程の式は前述の（５）式で表せます。
与えられた条件を（５）式に代入していくと、ポンプの全揚程\(H\)は下記のように求まります。 ただし、①、②間の圧力損失は無視できるとします。
ここで、吐出圧力ヘッドを求めてみますと、下記のとおりになります。 $$\frac {p_{2}}{\rho g}=\frac {280\times 1000}{1000\times 9.81}=28.5\ \textrm{m}$$
よって、全揚程は吐出圧（ヘッド）と異なることが定量的に証明できました。 $$H \neq\frac {p_{2}}{\rho g}$$
計算例２ 全揚程の算出（吸込側に圧力計がない場合）
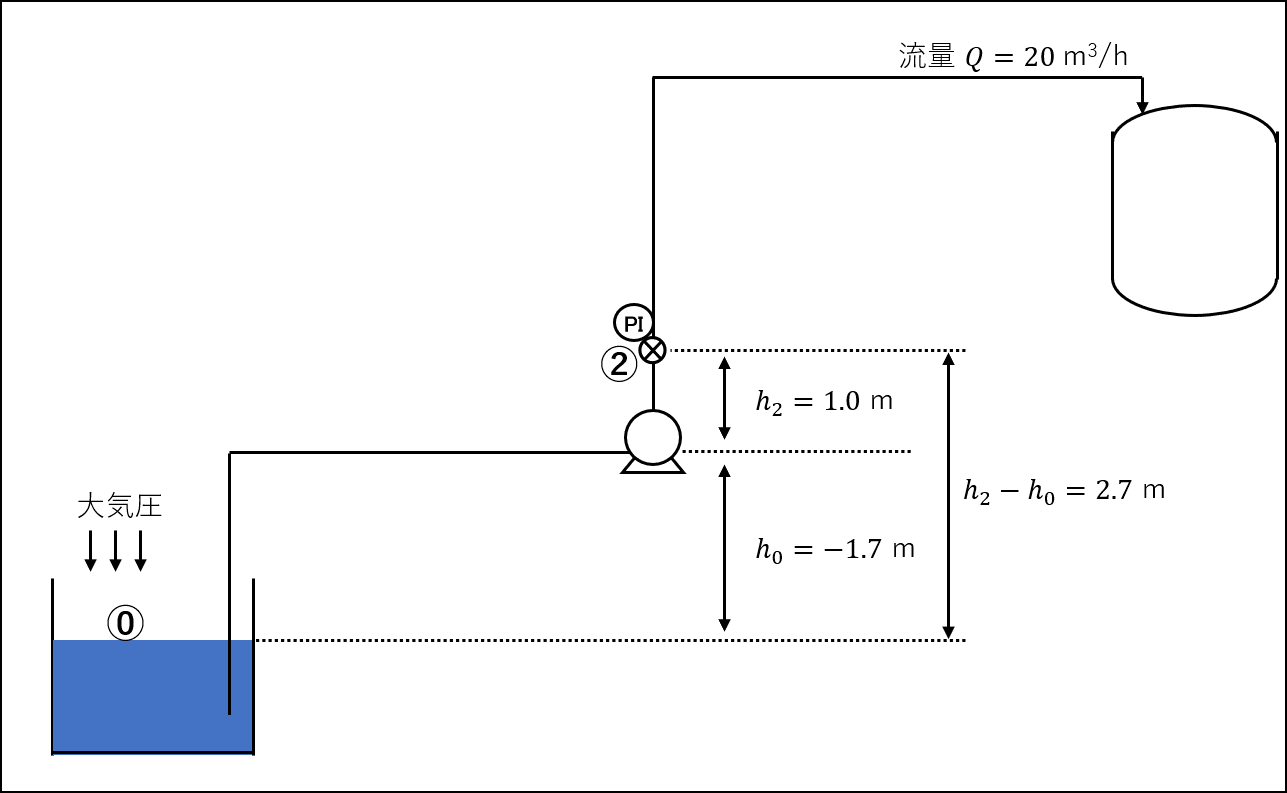
それでは、吸込側に圧力計がない場合について、ポンプの全揚程を計算していきましょう。
供給タンクの液面を⓪とし、点⓪－②間でエネルギー収支をとると、（４）式、（５）式は添字を１→０に変換した形となります。
したがって、与えられた条件を（５）式に代入すると、下記のように全揚程\(H\)が求まります。
このように吸込側の圧力計がない場合でも、ポンプの全揚程を求めることができました。
それでも合わない場合は、ポンプ能力が劣化している可能性があるよ。
計算例３ 全揚程の設計 その１（必要全揚程の算出）
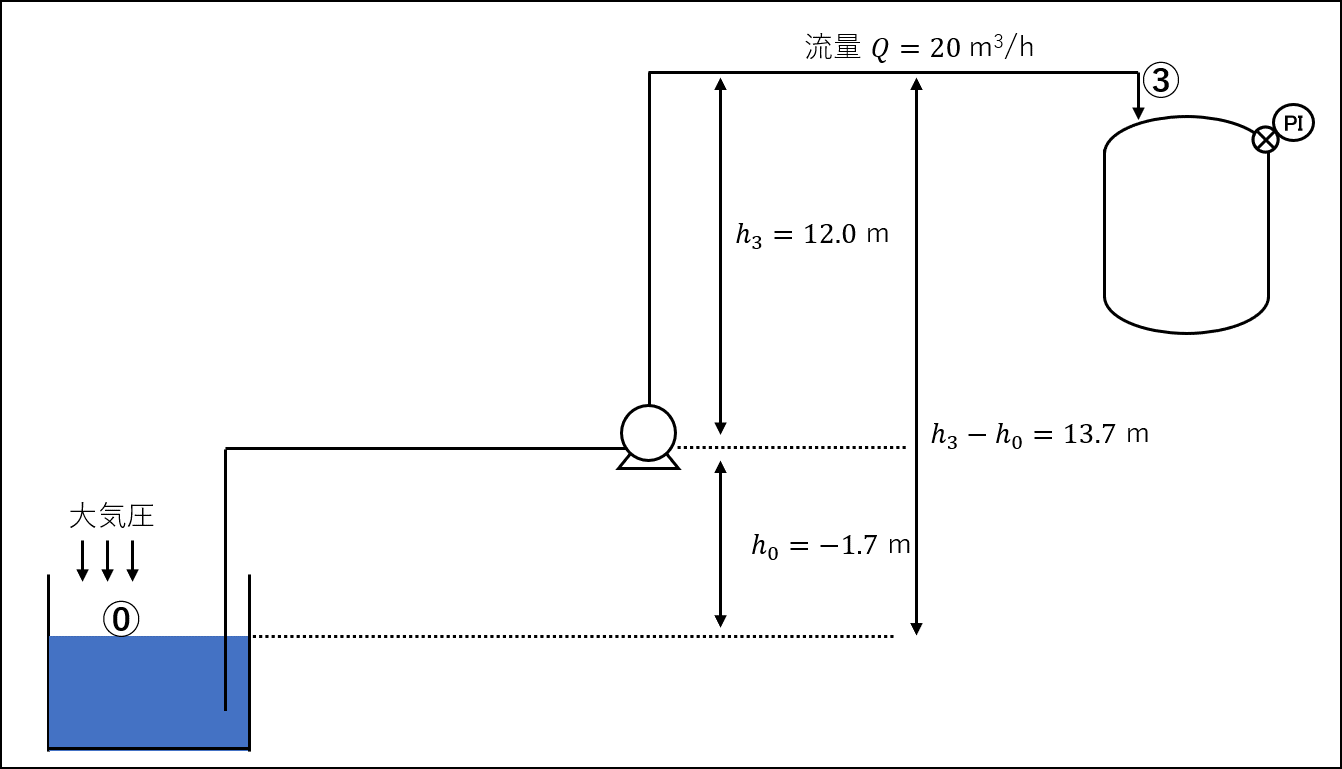
つぎは、供給タンクと送液タンクの条件から、必要全揚程を算出してみましょう。
送液タンク直近の配管部分を③とし、点⓪－③間でエネルギー収支をとると、（４）式、（５）式は添字を１→０、２→３に変換した形となります。
したがって、与えられた条件を（５）式に代入すると、下記のように全揚程\(H\)が求まります。
このように、供給タンク、送液タンクの条件がわかれば、ポンプの必要全揚程を算出できることがわかりました。
位置ヘッド差（実揚程）だけでポンプを設計してしまうと能力不足になるよ。
計算例４ 全揚程の設計 その２（必要全揚程の算出）
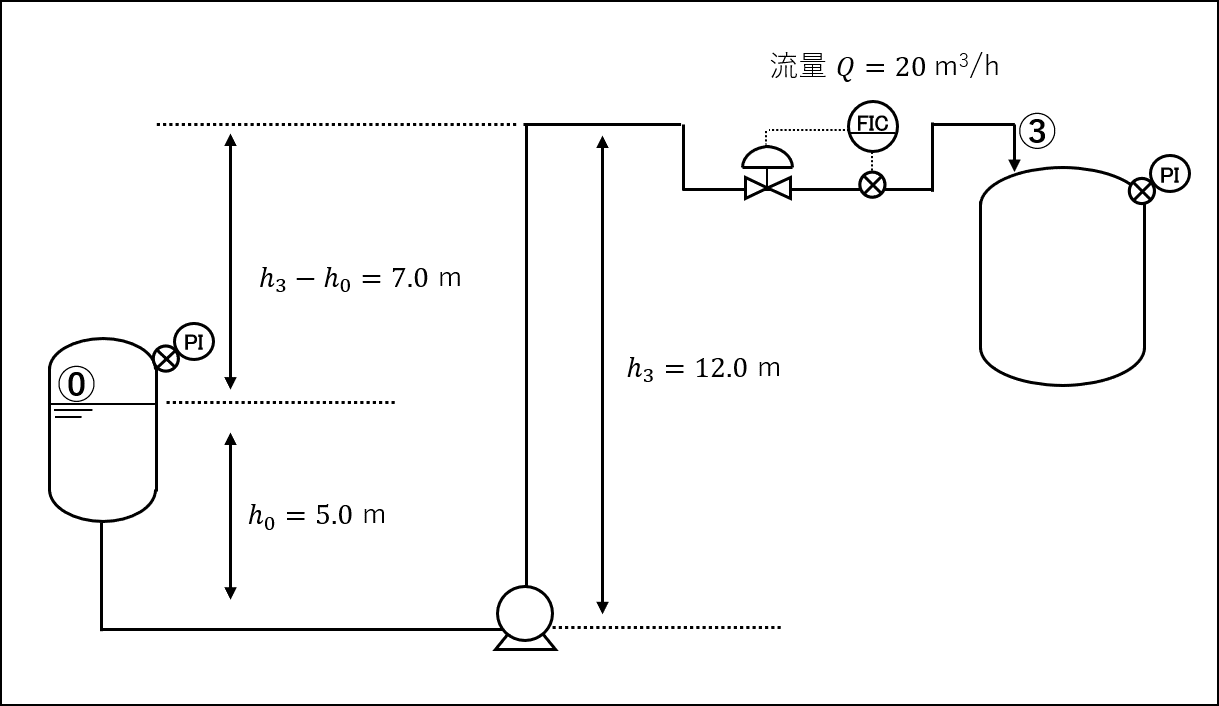
次は、少し条件をかえてポンプの必要全揚程を算出してみましょう。
今回も供給タンクと送液タンクの条件からポンプの必要全揚程を算出します。
今回はCV圧損を追加してみました。
計算例３と同様に、点⓪－③間でエネルギー収支をとり、与えられた条件を（５）式に代入すると、下記のように全揚程\(H\)が求まります。
このように、様々な条件でポンプの全揚程が計算できました。
また、実際の設計では余裕率を1.1~1.5の範囲で掛けて発注します。
＜＜配管の圧力損失計算＞＞
-
-
【解説】配管圧力損失の計算方法
続きを見る
＜＜バルブの圧力損失計算＞＞
-
-
【解説】コントロールバルブの圧力損失（Cv値）計算
続きを見る
まとめ
ポイント
- 全揚程\(H\)とは、ポンプによって流体が得た全エネルギー（ヘッド）のこと
- 全揚程は、流体のエネルギー収支式から求めることができる
- 全揚程\(H\)(m) ＝ 速度ヘッド差 ＋ 位置ヘッド差 ＋ 圧力ヘッド差 ＋ 損失ヘッド
-
$$\begin{multline}\textbf{全揚程}\ \ \ H=\frac {u^{2}_{2}-u^{2}_{1}}{2g}+\left( h_{2}-h_{1}\right) +\frac {p_{2}-p_{1}}{\rho g}+\Sigma F\end{multline}$$
参考文献
1.化学工学―解説と演習 化学工学会 (監修), 多田 豊 (編集)
2.絵とき「ポンプ」基礎のきそ-選定・運転・保守点検- 外山 幸雄 (著)
化学工学の教科書には、流体のエネルギー収支式であるベルヌイの式が必ず載っています。
しかし、流体のもつエネルギーについて具体的に解説している化学工学の教科書は見たことがありません。
よって、流体力学の本で勉強する必要がありますが、絵ときシリーズの「流体力学」であれば、初学者でも理解できると思います。
