あと、必要なサンプルサイズはどのくらいかな？
こんなお悩みを解決します。
どうも。こんにちは。ケミカルエンジニアのこーしです。
本日は、「現場で使える比率の差の検定」について、わかりやすく解説します。
この記事では、実務に沿った例題を使って解説しますので、現場で使える技術を身につけることができます。
また、現場でよく問題となるサンプルサイズの決め方についても解説しています。
「平均値の差の検定（ｔ検定）」については、下記の記事で解説しています。
-
-
【例題でわかる】現場で使えるｔ検定！
続きを見る
本記事の内容
- 母比率の推定
- 標本分布とは
- 比率の標本分布
- 比率の差の検定
- サンプルサイズの決め方（区間推定・検定力）
- 参考文献
この記事を書いた人
こーし(@mimikousi)
目次
母比率の推定
母比率の推定とは何なのか、早速例題を用いて解説します。
【例題①】母比率の推定
日本国民全体の内閣支持率を調べたい。
無作為に抽出した1,000人にアンケートを取って内閣支持率を調べたところ、60％でした。
このとき、国民全体の内閣支持率は何％と推定できるか。（信頼度95%とする）
製造現場に関係する例題を考えたのですが、思いつきませんでした。
後述の「比率の差の検定」では、不良品発生率の例で解説していきます。
それでは、例題①を解いてみましょう。
例題①における母比率とは、「日本国民全体の内閣支持率」です。
母比率をきっちり求めようとすると、日本国民全員に内閣を支持するかどうかを聞かないといけないため、確認することは現実的に不可能です。
そこで、少数のサンプル（標本）から得られた標本比率を用いて、母比率を推定することを考えます。
標本分布とは
無作為に抽出した1,000人の内閣支持率は、別の1,000人の内閣支持率と全く同じになるとは限りません。
よって、下図のようにサンプル（標本）の内閣支持率は分布を持つことがわかります。
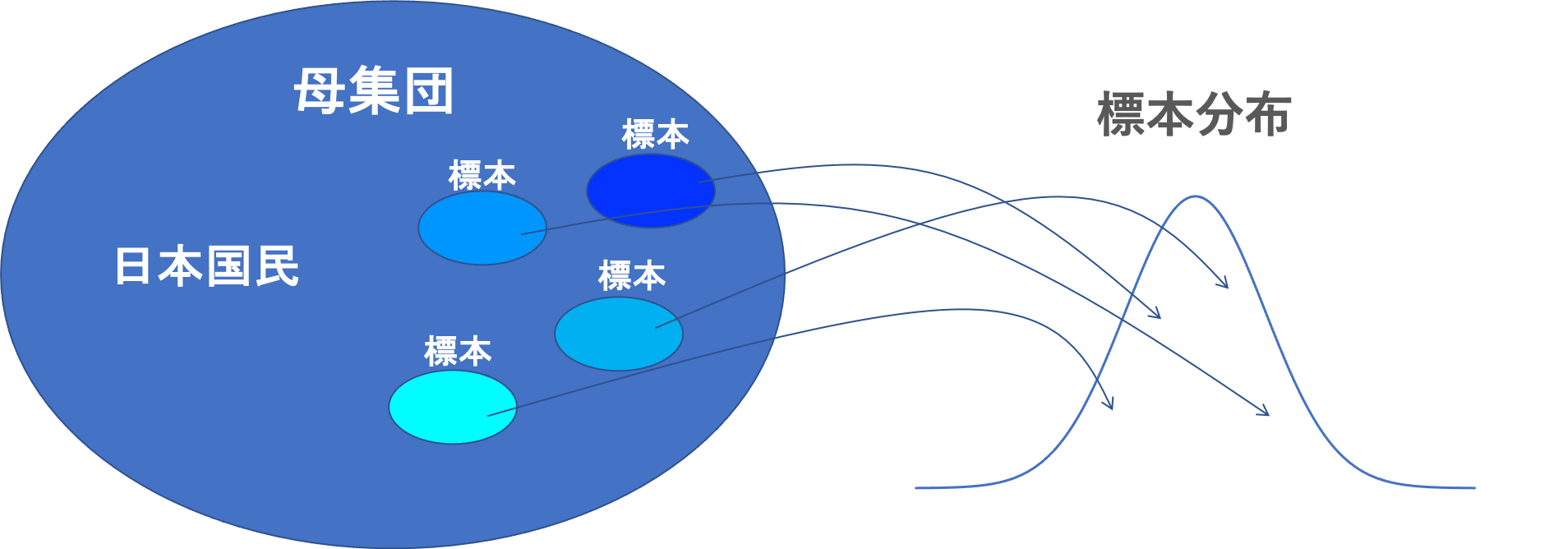
例えば下記のように、抽出した標本によって結果が異なりますので、標本比率は分布をもちます。
- サンプルAは、内閣支持率61%
- サンプルBは、内閣支持率56%
- サンプルCは、内閣支持率60%
- サンプルDは、内閣支持率65%
比率の標本分布
標本比率\(p\)の標本分布は、標本分散\(\sigma_{p}^2\)の正規分布（※）となります。
※実際は、二項分布やポアソン分布に従いますが、サンプル数（n）が十分に大きい時は、正規分布で近似できます。（中心極限定理）
標本比率\(p\)の標本分散\(\sigma_{p}^2\)は、サンプル数を\(n\)とすると、下式となります。
$$\sigma_{p}^2 = \frac{p(1-p)}{n}$$
標本の標準偏差\(\sigma_{p}\)は、標準誤差と呼ばれ、下式となります。
$$\sigma_{p} = \sqrt {\frac{p(1-p)}{n}}$$
上式からわかるように、標準誤差は、p=0.5（0≦p<≦1）のとき最大値を取り、サンプル数\(n\)が大きければ大きいほど小さくなります。
下図は、サンプルサイズが大きいときと小さいときの標本分布のイメージです。
サンプルサイズが大きくなると、標本比率は、母比率に近づき、バラツキ（標準誤差）は小さくなります。
一方、サンプルサイズが小さいと標本比率の取り得る値がバラツキやすくなります。
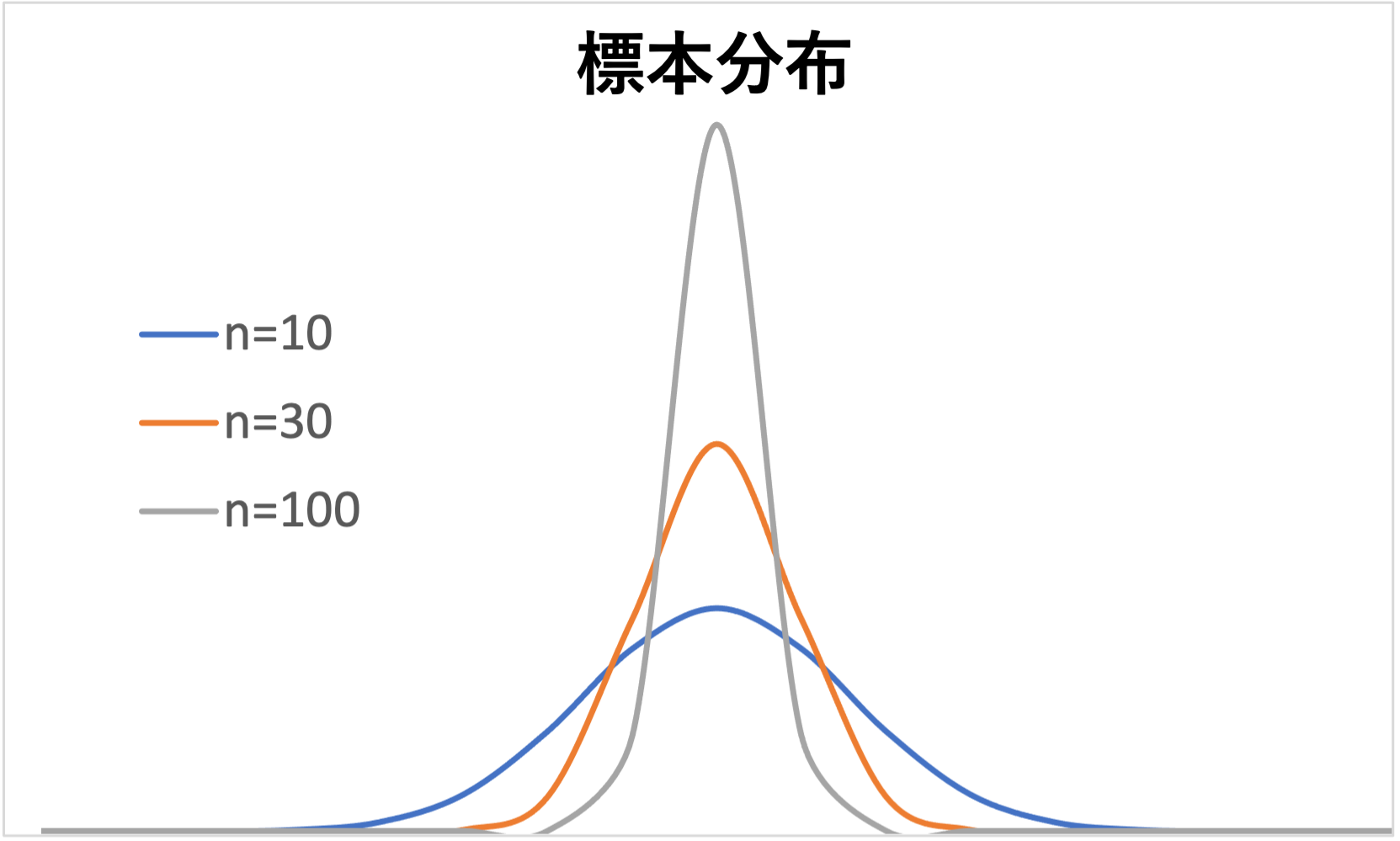
例えば、サンプルサイズを10人とすると、内閣支持率は0%もあれば、100%になる可能性もあります。
しかし、サンプルサイズを10,000人にすれば、0%や100％など極端な値になる可能性は低くなります。
よって、サンプルサイズによって標本分布のバラツキ（標準誤差）が変化します。
下図は、サンプルサイズを変更（n=10,30,100）したときの標本分布です。
サンプルサイズが小さいと、標本比率のバラツキが大きくなることがわかります。
母比率の推定
それでは、例題①のデータを用いて、母比率を推定してみましょう。
母比率の推定値を\(\hat{p}\)とすると、信頼度95%における信頼区間は、下記のように表せます。
$$p-1.96\sqrt{\frac{p( 1-p) }{n}} <\hat{p} <p+1.96\sqrt{\frac{p( 1-p) }{n}}$$
$$0.60-1.96\sqrt{\frac{0.60( 1-0.60) }{1000}} <\hat{p} <0.60+1.96\sqrt{\frac{0.60( 1-0.60) }{1000}}$$
$$0.57<\hat{p} <0.63$$
よって、日本国民全体の内閣支持率は、95%の信頼度で57〜63%であると推定できました。
この方法は、検定統計量\(z\)が、標準正規分布に従うことを利用しています。
$$z=\frac{\hat{p}-p}{\sqrt{\frac{p( 1-p) }{n}}}$$
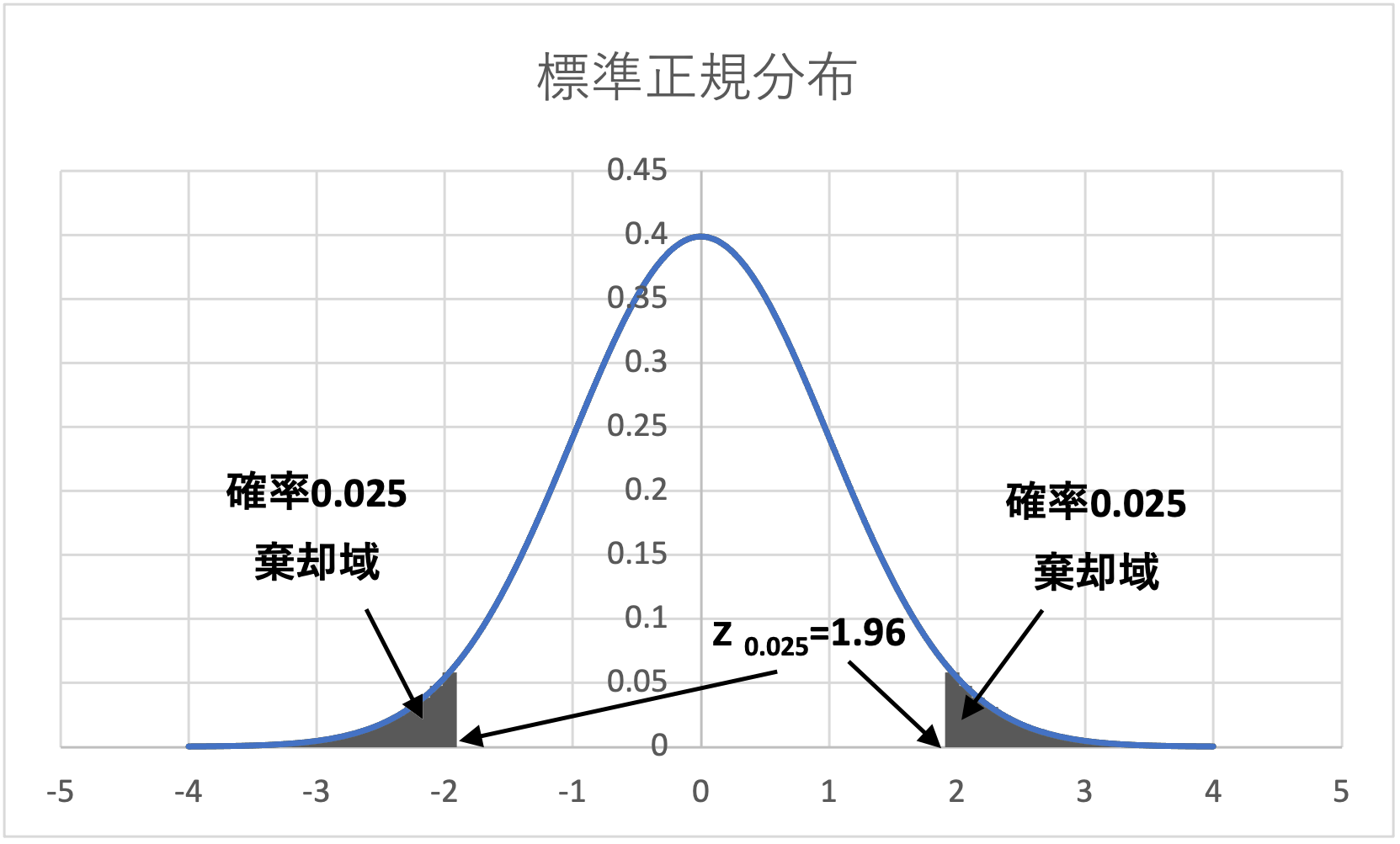
標準正規分布表を用いると、信頼度95%となる検定統計量は\(z=1.96\)となります。
（信頼度95%は、上側確率が2.5%(0.025)と同義です。下グラフ参照）
よって、下記のように信頼区間を求めることができます。
$$\left| z\right| <1.96$$
$$-1.96 <z <1.96$$
$$-1.96 <\frac{\hat{p}-p}{\sqrt{\frac{p( 1-p) }{n}}} <1.96$$
$$p-1.96\sqrt{\frac{p( 1-p) }{n}} <\hat{p} <p+1.96\sqrt{\frac{p( 1-p) }{n}}$$
ちなみに、信頼度95%のときの誤差範囲は下式のように表せます。
$$1.96\sqrt{\frac{p( 1-p) }{n}}$$
＝信頼度○％のｚ値 × 標準誤差
よって、誤差範囲は「信頼度を何％にするか」と、「標準誤差をいくつにするか」で決まることが分かります。
後述しますが、誤差範囲をいくつまで許容するのか設定することで、必要となるサンプル数を求めることができます。
比率の差の検定
検定とは
検定とは、2つの比率に「差が無い」と仮定した際の分布（帰無分布）に対し、得られたデータが分布のどの位置に該当するのかを確認し、「差があるかどうか」を判定する方法です。
検定の手順は下記の通りです。
- 仮説の設定
帰無仮説\(H_0\)と対立仮説\(H_1\)を設定
\(H_0:p_{1} = p_{2}\)
\(H_1:p_{1}\neq p_{2}\) - 検定統計量（z）の算出
- 棄却域の設定
まず有意水準\(\alpha\)（基本5%）を決め、棄却域を求める - 判定
正規分布表を読み取り、データから算出した検定統計量（z）が、
・棄却域に入る → 帰無仮説を棄却
・棄却域に入らない → 帰無仮説を採択 - 結論
それでは、具体的に検定を行ってみましょう。
母比率の検定
まず、母比率の検定を行います。
【例題②】母比率の検定
ある製品の不良品発生率はこれまで5%(\(=p_{0}\))でしたが、今月の不良品発生率は10%(\(=p\))となりました。
これが、偶然なのか、異常が発生しているのかを判断したいため、検定を行います。
有意水準は5％とし、サンプル数は100とします。
それでは、検定の手順に従い、例題を解いていきましょう。
1．仮説の設定
帰無仮説\(H_0 \)：\(p = p_{0}\) （不良品発生率は等しい）
対立仮説\(H_1 \)：\(p \neq p_{0}\) （不良品発生率は等しくない）
大きくても小さくても差があれば、「変化あり」ですので「両側検定」です。
2．検定統計量（ｚ）の算出
$$\begin{aligned}z&=\frac{p-p_{0}}{\sqrt {\frac{p_{0}(1-p_{0})}{n} }}\\[5pt]
&=\frac{0.10-0.05}{\sqrt{\frac{0.05(1-0.05)}{100}}}\\[5pt]
&=2.29\end{aligned}$$
3．棄却域の設定
有意水準は、\(\alpha = 0.05\left( 5\% \right)\)とします。
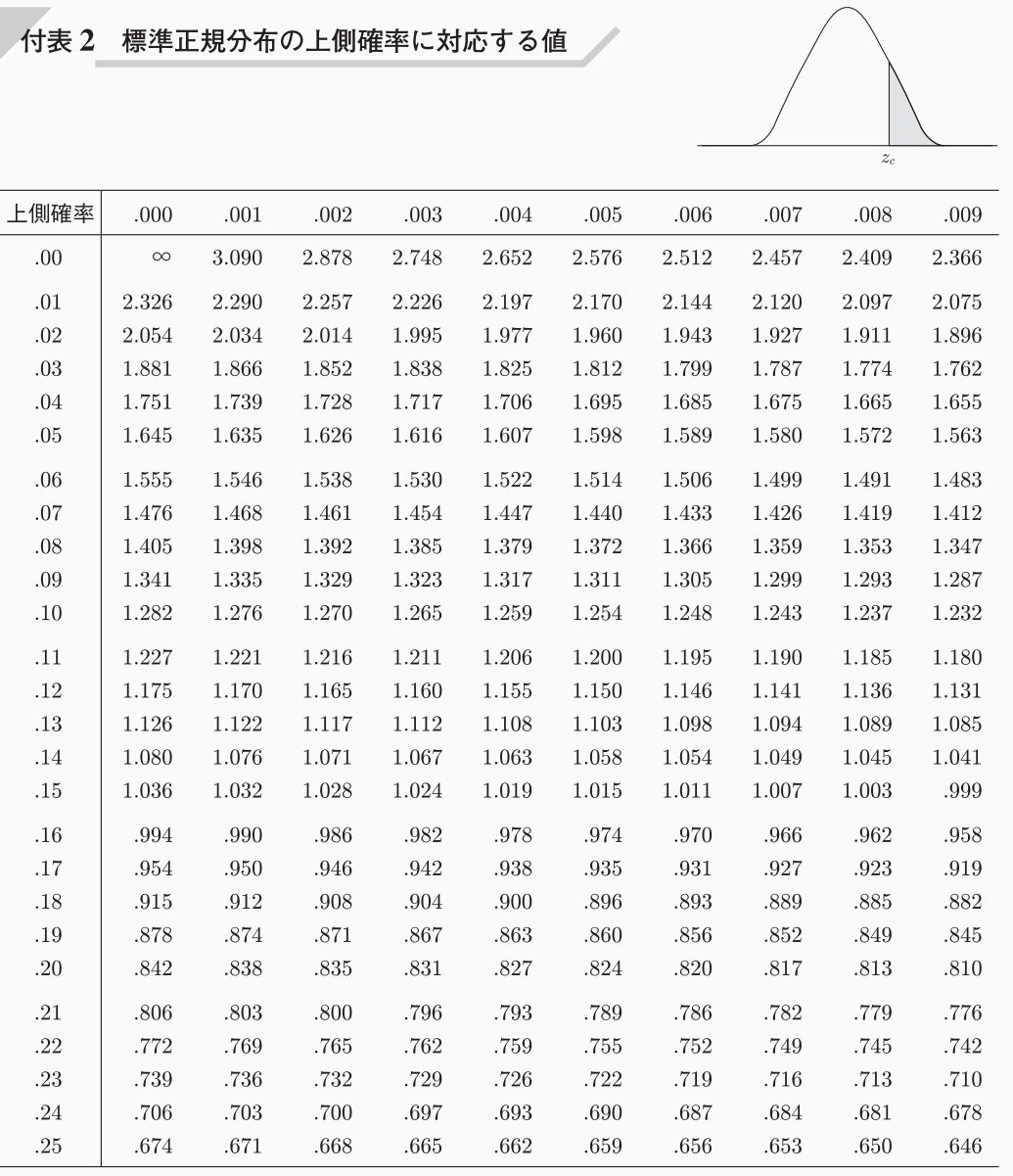
前述の正規分布表から、両側検定の有意水準\(\alpha = 0.05\)の点を求めます。
（両側検定なので、片側0.025ずつとなります）
よって、\(z_{0.025} = 1.96\)であり、棄却域は、\( z < -1.96,1.96<z\)となります。
4．判定
データから求めた検定統計量は、\(z=2.29 > 1.96\)となることから、検定統計量ｚは棄却域に入り、帰無仮説は棄却されます。
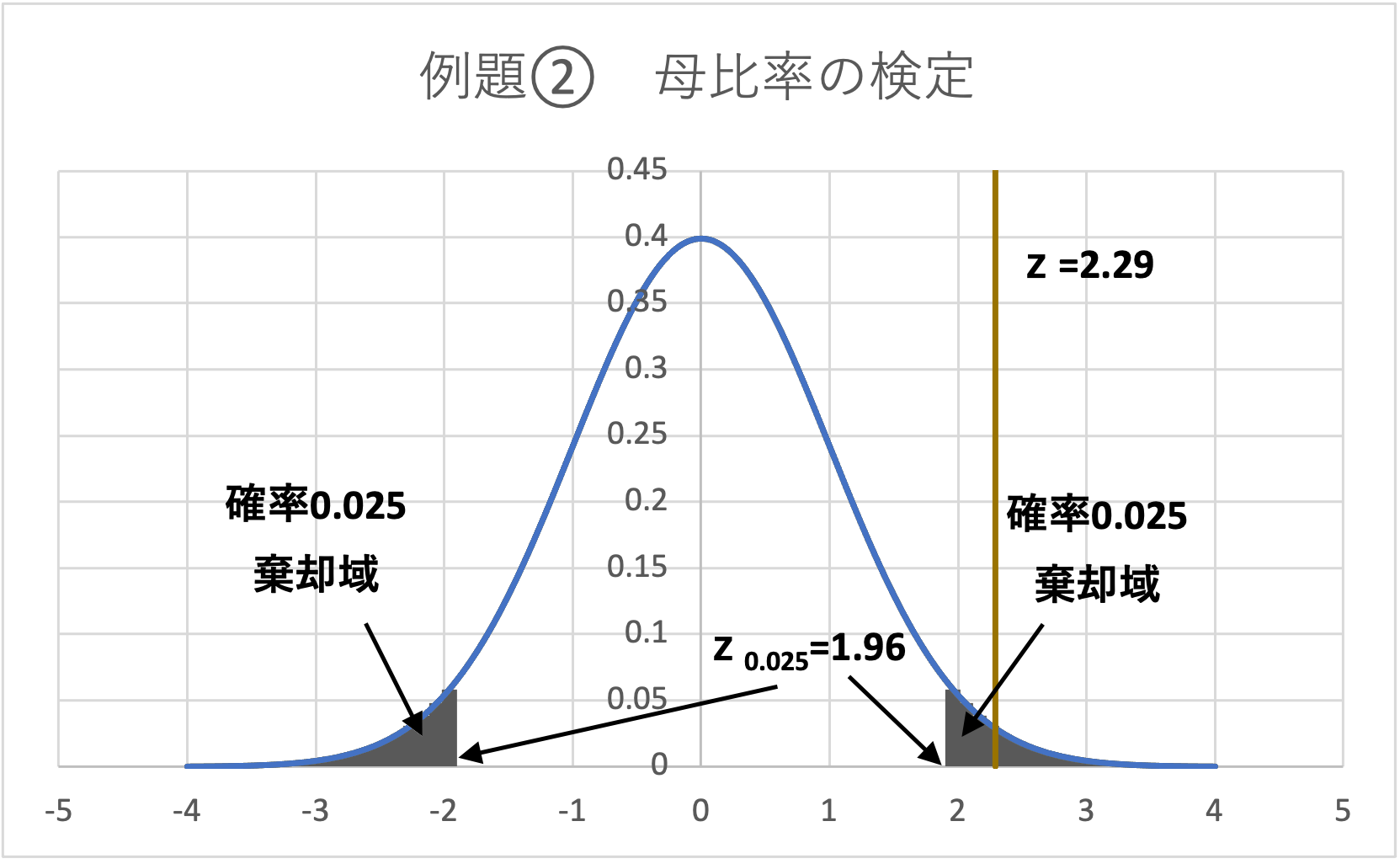
5．結論
帰無仮説が棄却されたため、何らかの理由でサンプルの不良品発生率は変化している（増加している）と言えます。
独立な２群の比率の差の検定
次に、独立な2群の比率の差を検定してみます。
「独立」とは、一方の起こる確率が他の（データ）群によって左右されない場合のことです。
それでは例題③を見ていきましょう。
【例題③】独立な2群の比率の差の検定
ある部品をメーカーA、もしくはメーカーBから購入することを検討しています。
それぞれ500個ずつテスト購入し、不良品率を調べたところ、メーカーAが3%で、メーカーBが1%でした。
メーカーAとメーカーBで不良品率に差があるかどうかを検定したいと考えています。
有意水準は5％とします。
それでは、検定の手順に従い、例題を解いていきましょう。
1．仮説の設定
帰無仮説\(H_0 \)：\(p_{1} = p_{2}\) （メーカーAとメーカーBの不良品率は等しい）
対立仮説\(H_1 \)：\(p_{1} \neq p_{2}\) （メーカーAとメーカーBの不良品発生率は等しくない）
大きくても小さくても差があれば、「変化あり」ですので「両側検定」です。
2．検定統計量（ｚ）の算出
2つの群（サンプル）を合わせた比率\(p\)を用います。
$$p=\frac{n_{1}p_{1}+n_{2}p_{2}}{n_{1}+n_{2}}=\frac{0.03*500+0.01*500}{500+500}=0.02$$
また、帰無仮説のもとでの\((p_{1} - p_{2})\)の標本分布の分散を\(s_{p_{1}-p_{2}}^2\)とすると、標準誤差\(s_{p_{1}-p_{2}}\)は、
$$s_{p_{1}-p_{2}}=\sqrt{p(1-p)(\frac{1}{n_{1}}+\frac{1}{n_{2}})}$$
となります。
よって、
$$\begin{aligned}z&=\frac{p_{1}-p_{2}}{\sqrt{p(1-p)(\frac{1}{n_{1}}+\frac{1}{n_{2}})}}\\[5pt]
&=\frac{0.03-0.01}{\sqrt{0.02(1-0.02)(\frac{1}{500}+\frac{1}{500})}}\\[5pt]
&=2.26\end{aligned}$$
3．棄却域の設定
有意水準は、\(\alpha = 0.05\left( 5\% \right)\)とします。
前述の正規分布表から、両側検定の有意水準\(\alpha = 0.05\)の点を求めます。
（両側検定なので、片側0.025ずつとなります）
よって、\(z_{0.025} = 1.96\)であり、棄却域は、\( z < -1.96,1.96<z\)となります。
4．判定
データから求めた検定統計量は、\(z=2.26 > 1.96\)となることから、検定統計量ｚは棄却域に入り、帰無仮説は棄却されます。
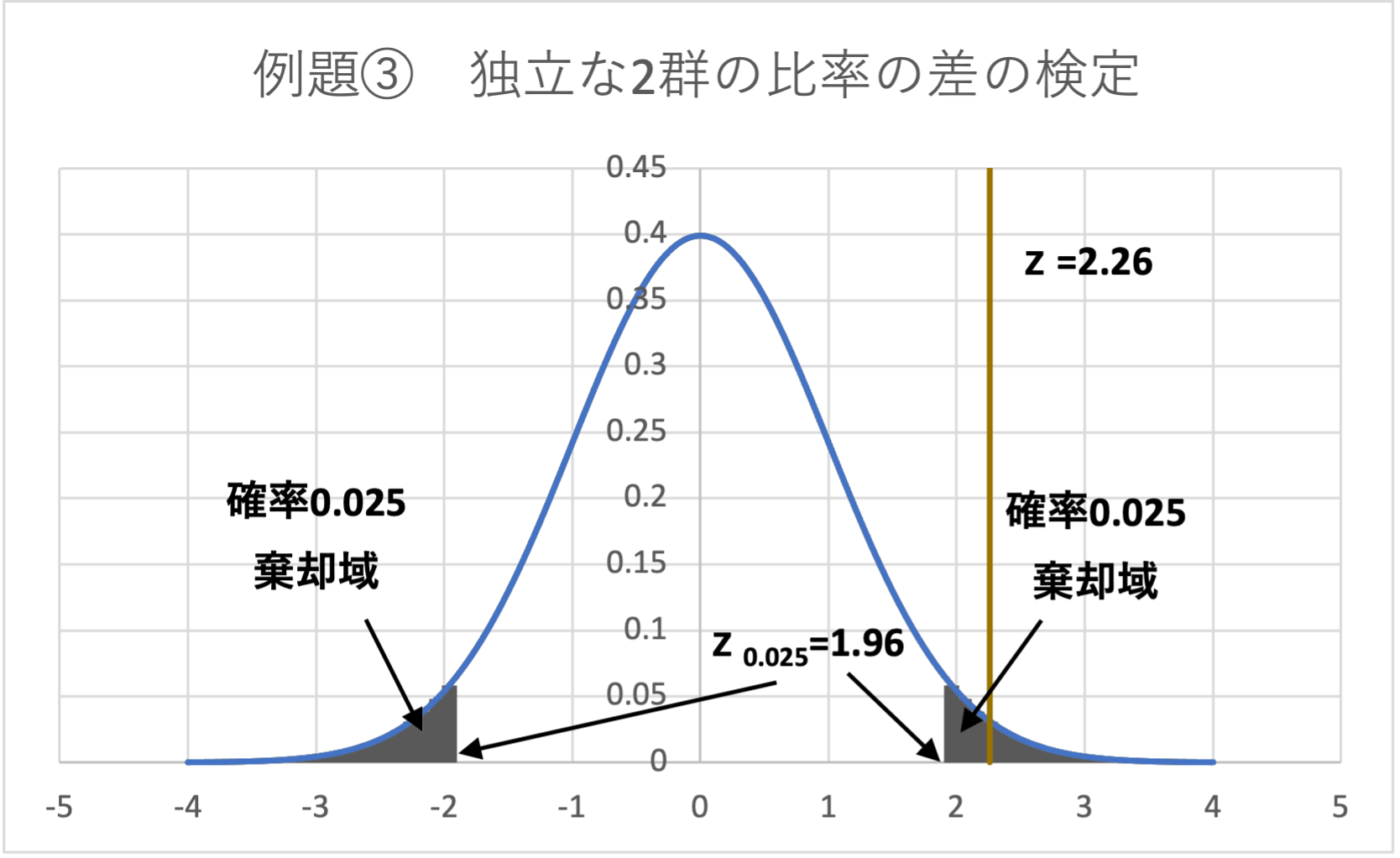
5．結論
帰無仮説が棄却されたため、メーカーAとメーカーBの不良品発生率は異なる（メーカーBの方が不良品発生率が低い）と言えます。
対応のある２群の比率の差の検定
続いて、対応のある2群について考えていきましょう。
対応のある2群とは、互いに独立でなく、対応関係（相関）がある2群のことです。
【例題④】対応のある2群の比率の差の検定
ある製品の製品検査を分析方法Aと分析方法Bで同時に行いました。
分析方法Aと分析方法Bの検査結果（不良品発生率）に有意差があるかどうかを検定します。
【検査結果】
| 分析方法A | 分析方法B | 計 | |
| 正常品 | 不良品 | ||
| 正常品 | 983(=\(n_{11}\)) | 10(=\(n_{12}\)) | 993 |
| 不良品 | 2(=\(n_{21}\)) | 5(=\(n_{22}\)) | 7 |
| 計 | 985 | 15 | 1000 |
それでは、検定の手順に従い、例題を解いていきましょう。
ちなみに、同じ製品を検査していますので、対応のある2群と見なします。
また、対応のある2群のケースでは、どちらか一方だけが「不良品」と判定したものの数（\(n_{12},n_{21}\)）が、有意に隔たっているかどうかを検定します。
1．仮説の設定
帰無仮説\(H_0 \)：\(n_{12} = \frac{n_{12}+n_{21}}{2}\) （どちらか一方だけが不良品と判定したものの数が同じである）
対立仮説\(H_1 \)：\(n_{12} \neq \frac{n_{12}+n_{21}}{2}\) （どちらか一方だけが不良品と判定したものの数に隔たりがある）
大きくても小さくても差があれば、「変化あり」ですので「両側検定」です。
2．検定統計量（ｚ）の算出
$$\begin{aligned}z&=\frac{n_{12}-\frac{n_{12}+n_{21}}{2}}{\frac{\sqrt{n_{12}+n_{21}}}{2}}\\[5pt]
&=\frac{10-\frac{10+2}{2}}{\frac{\sqrt{10+2}}{2}}\\[5pt]
&=2.31\end{aligned}$$
3．棄却域の設定
有意水準は、\(\alpha = 0.05\left( 5\% \right)\)とします。
下図の正規分布表から、両側検定の有意水準\(\alpha = 0.05\)の点を求めます。
（両側検定なので、片側0.025ずつとなります）
よって、\(z_{0.025} = 1.96\)であり、棄却域は、\( z < -1.96,1.96<z\)となります。
4．判定
データから求めた検定統計量は、\(z=2.31 > 1.96\)となることから、検定統計量ｚは棄却域に入り、帰無仮説は棄却されます。
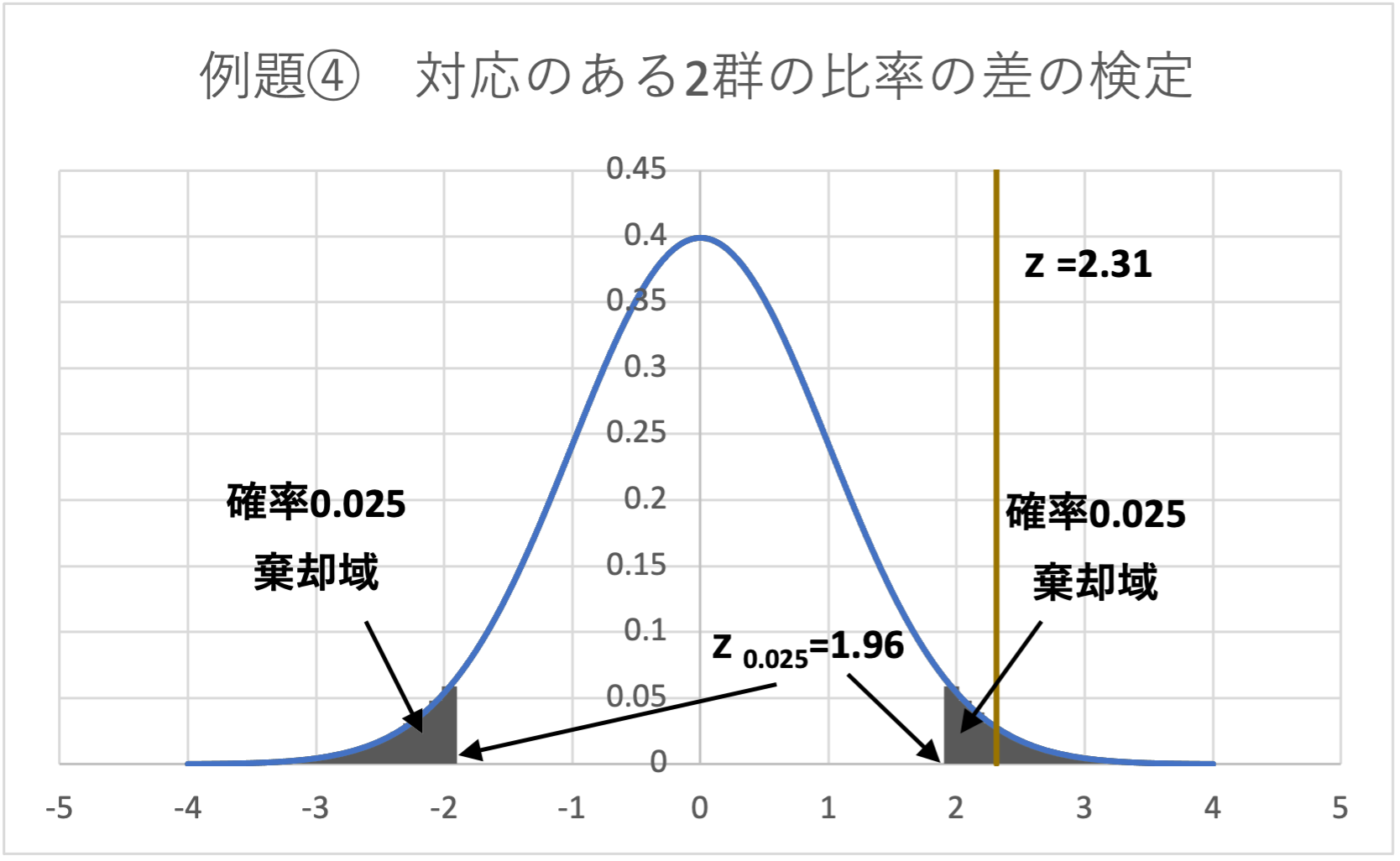
5．結論
帰無仮説が棄却されたため、分析方法Aと分析方法Bの検査結果（不良品発生率）は異なると言えます。
サンプルサイズの決め方
必要なサンプルサイズの決め方には、大きく分けて２通りの方法があります。
①区間推定に基づく方法（標準誤差）
②検定力に基づく方法
区間推定に基づく方法（標準誤差）
例題①で少し触れましたが、母比率の推定における誤差範囲は下記の通り表すことができます。
（許容）誤差範囲＝信頼度○％のｚ値 × 標準誤差
標準誤差\(\sigma_{p}\)は、
$$\sigma_{p} = \sqrt {\frac{p(1-p)}{n}}$$
よって、「許容誤差範囲」と「信頼度○％」を決定すれば、必要なサンプルサイズは自ずと決まってきます。
ちなみに、\(p(1-p)\)はp=0.5のときに最大値0.25を取るので、\(p(1-p)=0.25\)とすると、最大サンプル数が求まります。
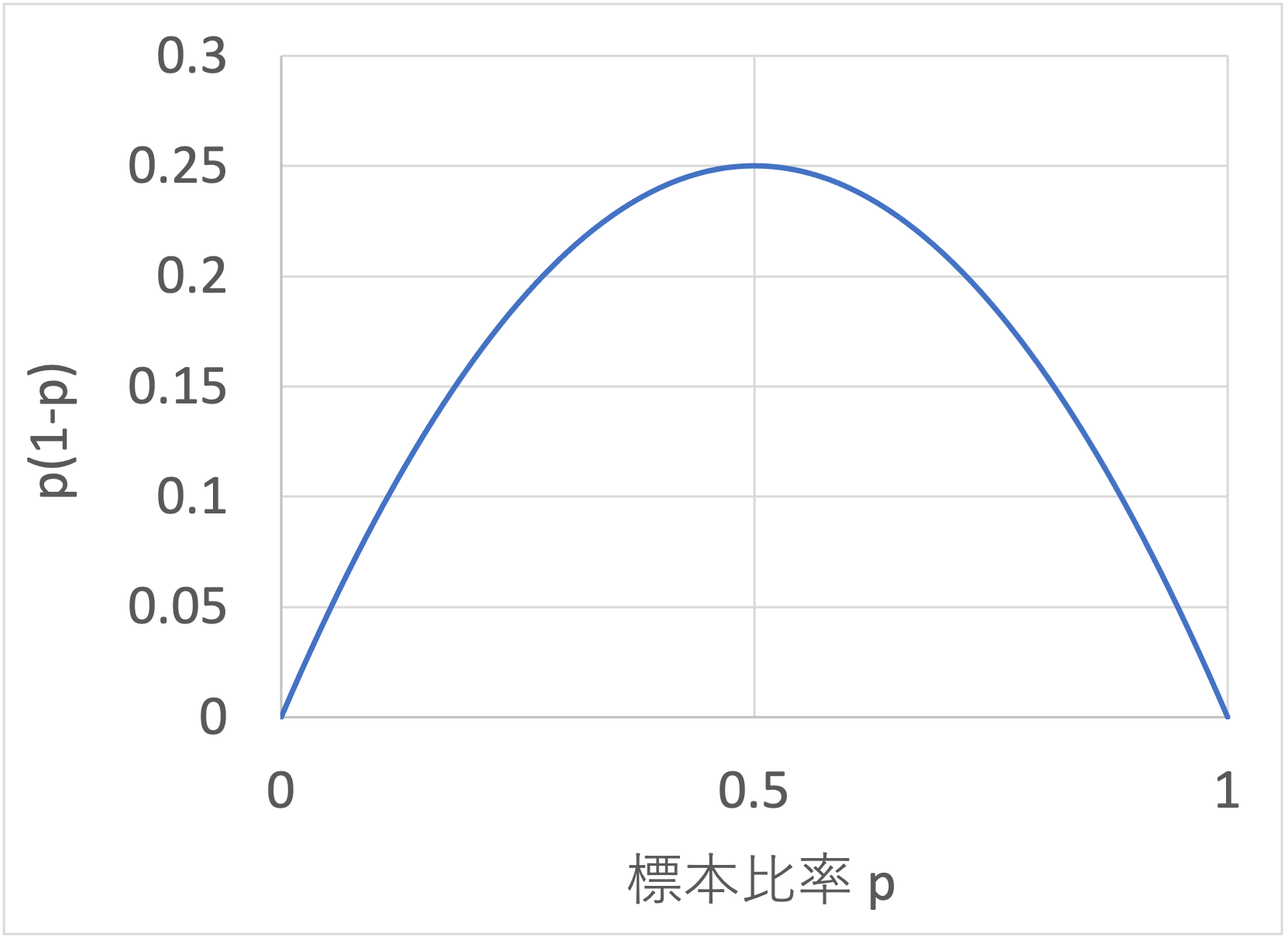
それでは、一つ例題を解いてみましょう。
【例題⑤】区間推定に基づく方法（標準誤差）
ある製品の不良品発生率\(p\)を信頼度95%で推定したい。
許容誤差範囲を１%とすると、サンプルサイズはいくつにしたらよいでしょうか。
信頼度95%のときのｚ値は1.96ですので、下記のように必要サンプルサイズを決めていきます。
$$\begin{aligned}0.01&=1.96\sqrt{\frac{p(1-p)}{n}}\\[5pt]
0.01&=1.96\sqrt{\frac{0.25}{n}}\\[5pt]
\frac{0.01}{1.96}&=\sqrt{\frac{0.25}{n}}\\[5pt]
\left( \frac{0.01}{1.96}\right ) ^{2}&=\frac{0.25}{n}\\[5pt]
n&=0.25\times \left ( \frac{1.96}{0.01}\right ) ^{2}\\[5pt]
n&=9604\end{aligned}$$
よって、必要なサンプル数は9604であることがわかりました。
しかし、この計算は\(p(1-p)\)が最大となる不良品発生率0.5(50%)を想定しており、余裕を見て計算しています。
そこで、不良品発生率を実際に近い値0.03（3%）を用いて計算してみると、
$$p(1-p)=0.03\times 0.97=0.0291$$
となりますので、
$$\begin{aligned}0.01&=1.96\sqrt{\frac{p(1-p)}{n}}\\[5pt]
0.01&=1.96\sqrt{\frac{0.0291}{n}}\\[5pt]
\frac{0.01}{1.96}&=\sqrt{\frac{0.0291}{n}}\\[5pt]
\left ( \frac{0.01}{1.96}\right ) ^{2}&=\frac{0.0291}{n}\\[5pt]
n&=0.0291\times \left ( \frac{1.96}{0.01}\right ) ^{2}\\[5pt]
n&=1118\end{aligned}$$
よって、必要なサンプル数は1118まで減少しました。
検定力に基づく方法
検定力とは、帰無仮説が誤っているときに、正しく帰無仮説を棄却できる確率のことです。
一方、有意水準\(\alpha \)というのは、帰無仮説が合っているのに帰無仮説を棄却してしまう確率です。
つまり、仮説検定においては、下記のように「２種類の誤り」が想定されます。
2種類の誤り
①第１種の誤り：帰無仮説が正しいのに、それを棄却する
②第２種の誤り：帰無仮説が誤っているのに、帰無仮説を採択する
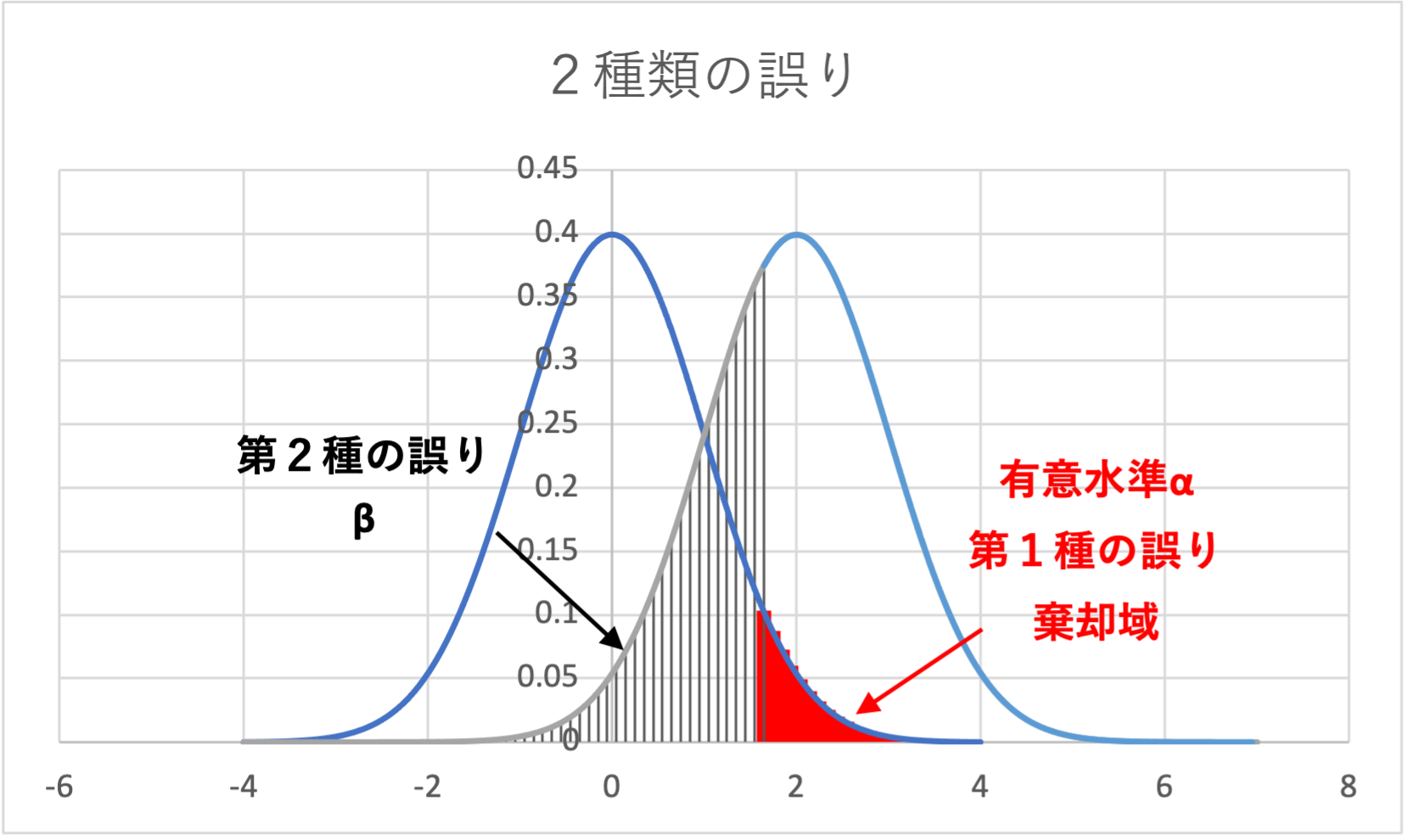
上図の左の分布が帰無仮説が正しいときの分布（帰無分布）であり、右の分布が帰無仮説が異なる場合の分布です。
帰無仮説が異なる場合（右の分布）、帰無分布（左の分布）の棄却域よりも内側に入ってしまう部分は、「第２種の誤り」（縦線部分）となります。
よって、有意水準\(\alpha\)だけでなく、第２種の誤り\(\beta\) も十分小さくなるようにサンプルサイズを決定する必要があります。
検定力は\(1 - \beta\)で表すことができ、図示すると下図のようになります。
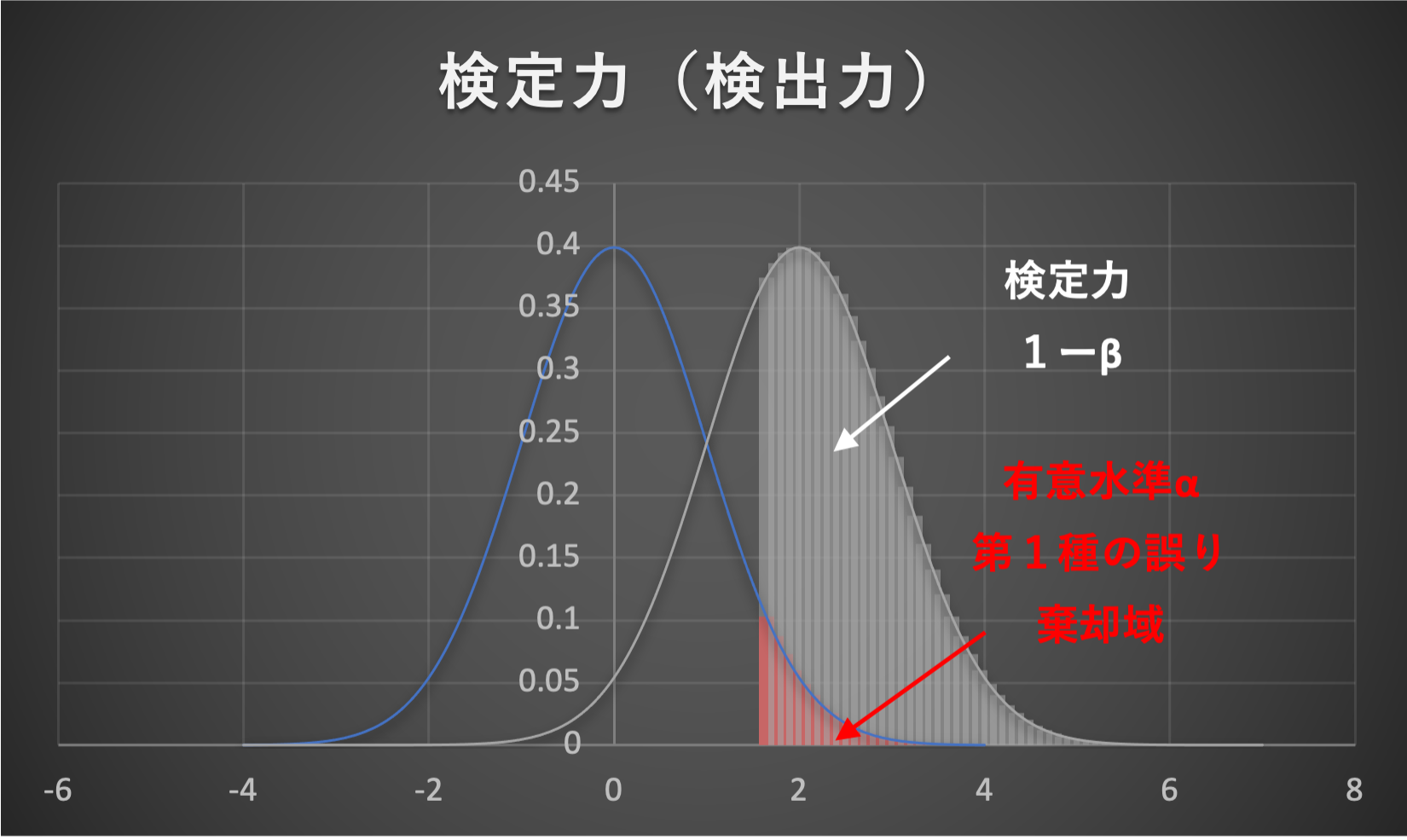
それでは、実際に例題を解いてみましょう。
【例題⑥】検定力に基づく方法
ある製品の不良品発生率はこれまで5%(\(=P\))でしたが、今月の不良品発生率は10%(\(=P_0\))となりました。
これが、偶然なのか、異常が発生しているのかを判断したいため、検定を行います。
有意水準は5％とし、検定力が0.90となるサンプル数を求めてみましょう。
検定力が0.90ということは、何らかの理由で不良品発生率が増加している場合、90%の確率で「差がある」と正しく検定できます。
ちなみに、有意水準が5%ということは、不良品発生率が変化していない場合、5%の確率で「差がある」と誤って検定する可能性があります。
まず、検定力\(1 - \beta\)を求める式を導出します。
検定力は、帰無仮説が正しくない場合ですので、今月の不良品発生率\(P_0\)を用いた検定統計量\(z_0\)は、標準正規分布\(N(0,1^2)\)に従いません。
$$z_0 = \frac{\hat P-P_0}{\sqrt{P_0(1-P_0)/n}}$$
よって、対立仮説でも標準正規分布\(N(0,1^2)\)に従う検定統計量\(z\)の形に式変形します。（母比率\(P\)の帰無分布）
$$z = \frac{\hat P-P}{\sqrt{P(1-P)/n}}$$
&=\Pr \left\{ \frac{\hat{P}-P_{0}}{\sqrt{P_{0}\left( 1-P_{0}\right) /n}}\leq -z_{\frac{\alpha}{2} }\right\} +\Pr \left\{\frac{\hat{P}-P_{0}}{\sqrt{P_{0}\left( 1-P_{0}\right) /n}} \geq z_{\frac{\alpha}{2}}\right\} \\[5pt]
&=\Pr \left[ \left\{ \frac{\hat{P}-P}{\sqrt{P\left( 1-P\right) /n}}+\frac{P-P_{0}}{\sqrt{P\left( 1-P\right) /n}}\right\} \sqrt{\frac{P\left( 1-P\right) }{P_{0}\left( 1-P_{0}\right) }}\leq -z_{\frac{\alpha}{2}}\right]+\Pr \left[ \left\{ \frac{\hat{P}-P}{\sqrt{P\left( 1-P\right) /n}}+\frac{P-P_{0}}{\sqrt{P\left( 1-P\right) /n}}\right\} \sqrt{\frac{P\left( 1-P\right) }{P_{0}\left( 1-P_{0}\right) }}\ge z_{\frac{\alpha}{2}}\right]\\[5pt]
&\approx \Pr \left( z\leq -z_{\frac{\alpha}{2}}A-B\right) +\Pr \left( z\ge z_{\frac{\alpha}{2}}A-B\right) \\[5pt]
\end{aligned}$$
$$A = \sqrt{\frac{P_{0}\left( 1-P_{0}\right) }{P\left( 1-P\right) }}$$
$$B = \frac{P-P_0}{\sqrt{P(1-P)/n}}$$
検定統計量\(z_0\)の分布が、有意水準と重なる部分が検定力です。
そこで、\(z_0\)を標準正規分布に従う\(z\)に変換してやることで、検定力を求めることができます。
図解すると下図の通りです。
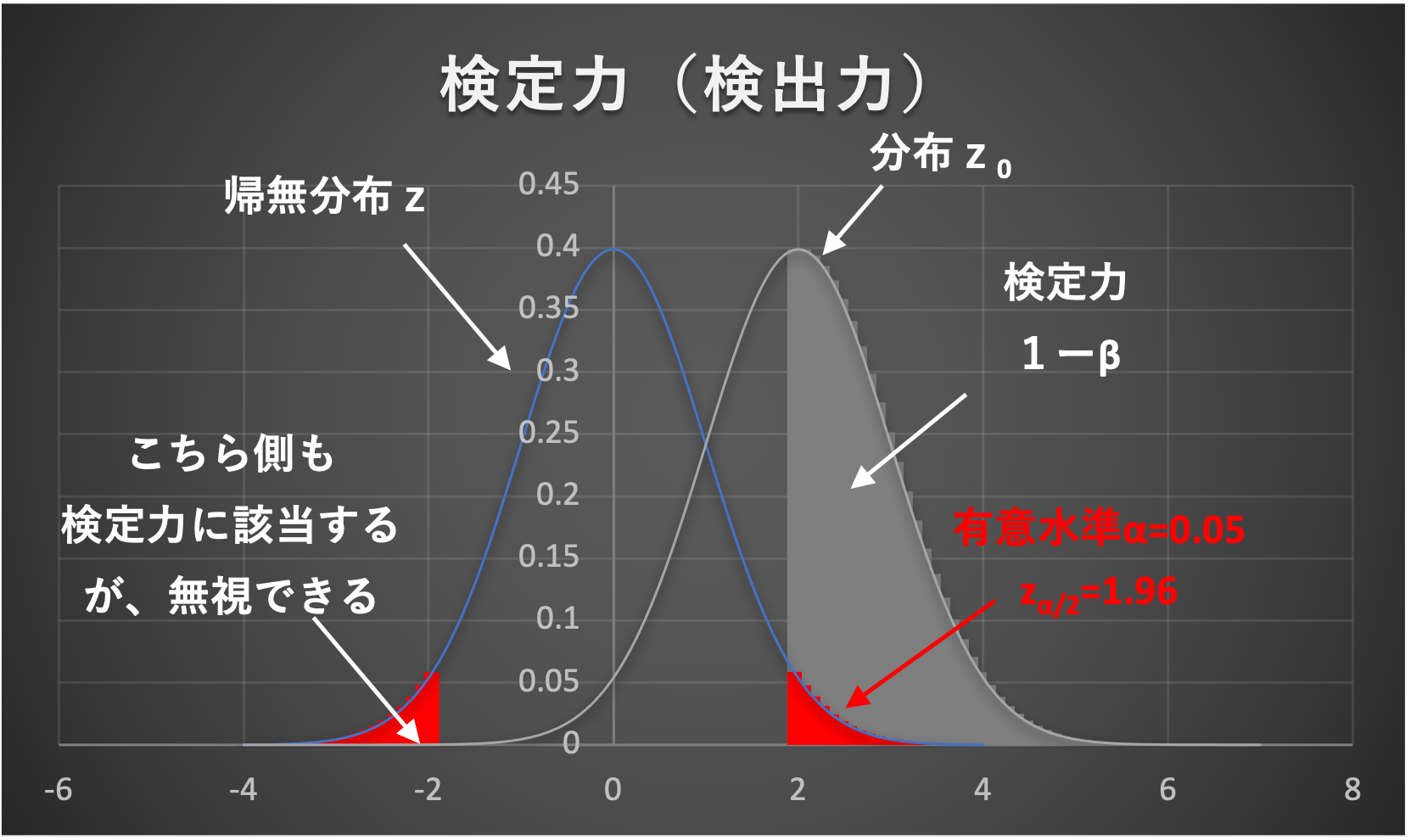
それでは、例題⑥を実際に計算してみましょう。
$$\begin{aligned}A&= \sqrt{\frac{P_{0}\left( 1-P_{0}\right) }{P\left( 1-P\right) }}\\[5pt]
&=\sqrt{\frac{0.1\times0.9}{0.05\times 0.95}}\\[5pt]
&=1.376\end{aligned}$$
$$\begin{aligned}B& = \frac{P-P_0}{\sqrt{P(1-P)/n}}\\[5pt]
&=\frac{0.05-0.10}{\sqrt{0.05\times 0.95/n}}\\[5pt]
&=-0.229\sqrt{n}\end{aligned}$$
検定力\(1 - \beta = 0.90\)より、
$$0.90 = \Pr \left( z\leq -z_{\frac{\alpha}{2}}A-B\right) +\Pr \left( z\ge z_{\frac{\alpha}{2}}A-B\right) $$
上図より、右辺第2項は無視できるほど小さいので、
$$0.90 = \Pr \left( z\leq -1.96\times 1.376 -(-0.229\sqrt{n})\right) $$
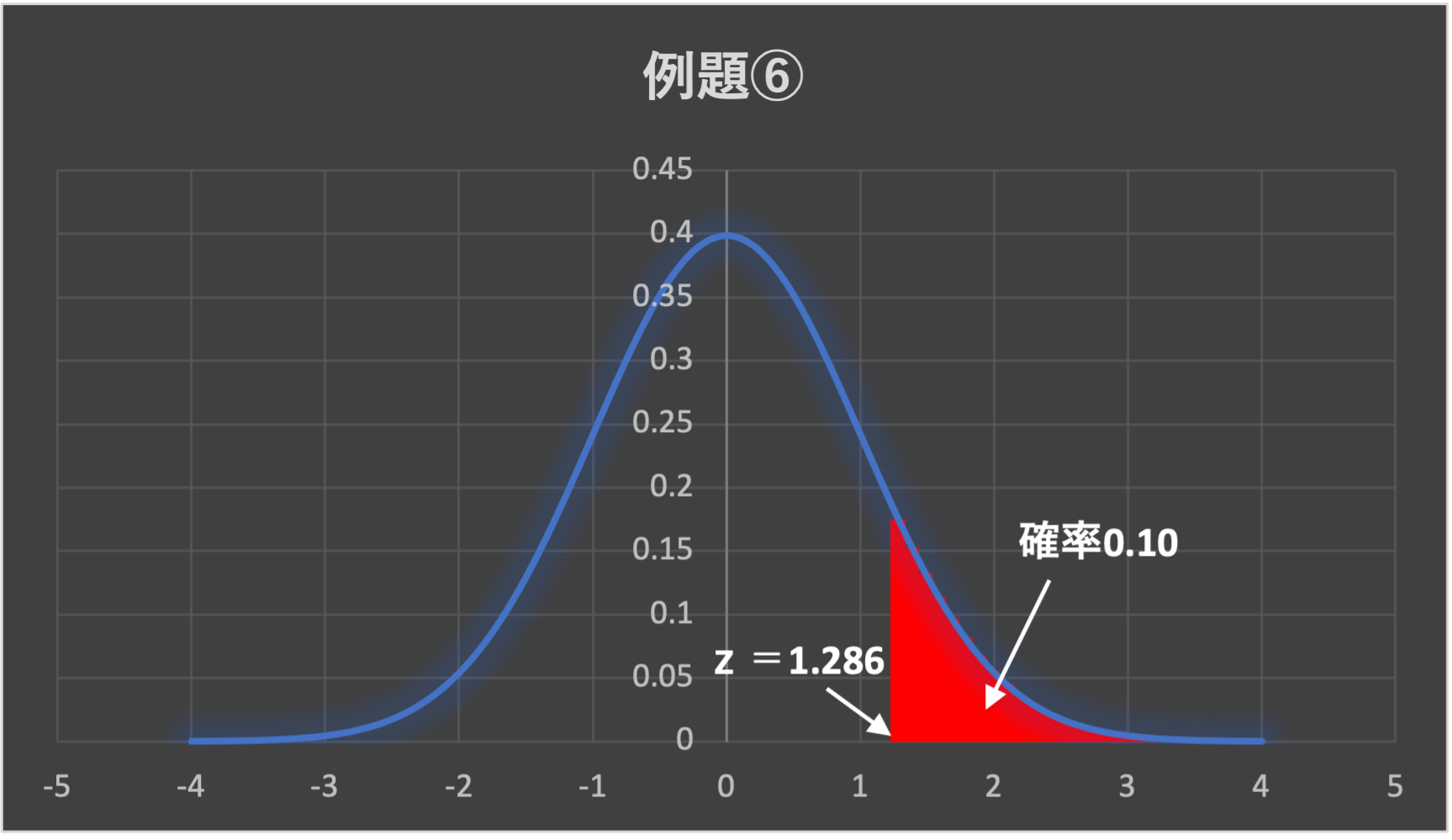
標準正規分布表より、上式を満たすのは\(z=1.282\)のときであるため、
$$\begin{aligned}1.282&\leq -1.96\times 1.376 -(-0.229\sqrt{n})\\[5pt]
0.229\sqrt{n}&\ge 1.282+1.96\times 1.376\\[5pt]
\sqrt{n}&\ge \frac{1.282+1.96\times 1.376}{0.229}\\[5pt]
n&\ge 301.9\end{aligned}$$
よって、必要なサンプル数は302ということがわかりました。
参考文献
1．心理統計学の基礎（有斐閣アルマ）統計検定2級〜準1級レベル
本記事では、この本を大いに参考にさせてもらいました。
初級から中級レベルに運んでくれるような、非常に詳しい解説があります。
特に「検定力分析によるサンプルサイズの決定」、「線形モデルの基礎」の解説が好きです。
例題を作成する上で参考にしました。
製造現場で品質管理をする方にオススメです。
3. サンプルサイズの決め方
サンプルサイズの決め方については、こちらの教科書も参考にしました。
やや難しめなので、心理統計学の基礎で基礎を身につけた上で、読むことをオススメします。
