【簡単】オリフィスの流量計算方法を解説！

どうも。こんにちは。
ケミカルエンジニアのこーしです。

本日は、オリフィスの流量計算方法についてわかりやすく解説していきます。

この記事を読むことで、オリフィスの流量計算とオリフィス孔径の設計ができるようになります。

この記事を書いた人

こーし(@mimikousi)

オリフィスの流量計算方法

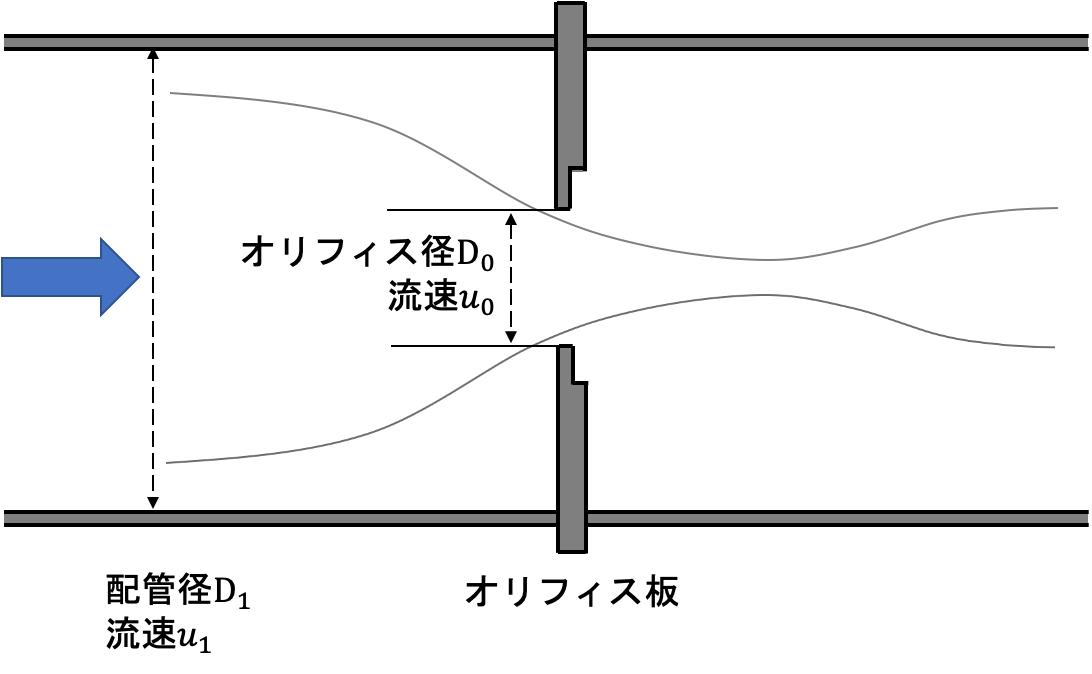
オリフィスの流量計算式

オリフィスの流量計算式は、下式の通りです。

オリフィス流量計は、オリフィス前後の差圧 \(\Delta p\)を測定することで、流量\(Q\)を算出しています。

流量係数\( C\)の参考値

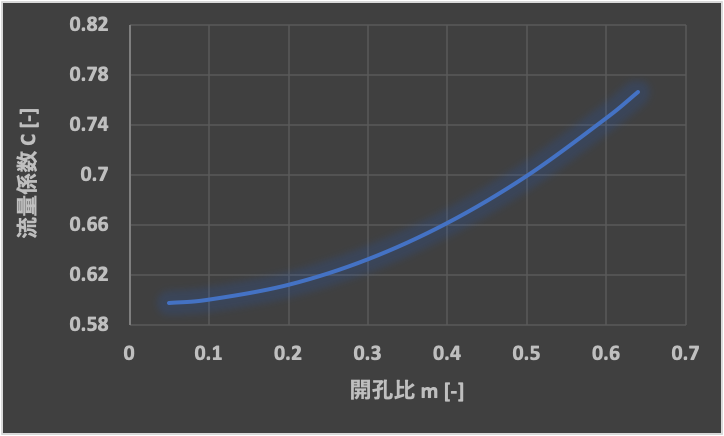
流量係数\(C\)の参考値は、上のグラフを読み取ります。

数式で表すと、下式の通りです（化学工学便覧改訂六版　P.324参照）。

流量係数\(C\)は、開孔比\(m\)とレイノルズ数\(Re\)の関数になりますが、限界レイノルズ数\(Re_{T}\)以上では、(2)式のように開孔比\(m\)のみの関数となります。

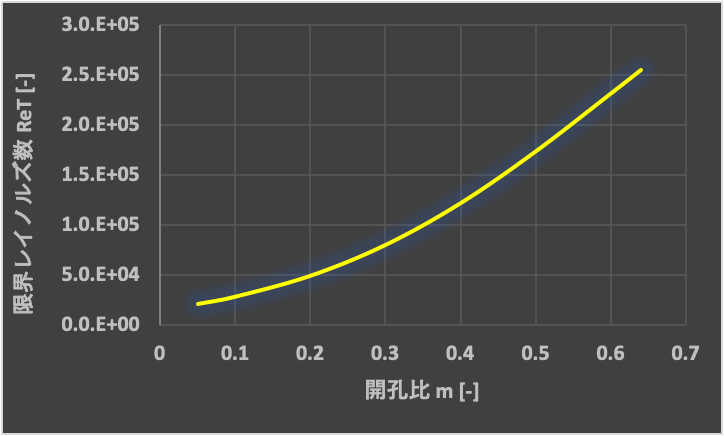
限界レイノルズ数\(Re_{T}\)は、開孔比\(m\)の関数となり、上のグラフのように書けます。

数式で表すと、下式の通りです。

$$Re_{T}= 10^{4.185+2.831m-1.438m^{2}}\tag{3}$$

よって、レイノルズ数\(Re\)が限界レイノルズ数\(Re_{T}\)よりも大きい場合は、(2)式を使って流量係数\(C\)を求めることができます。

ある程度の流速が確保されている場合、レイノルズ数\(Re\)は、限界レイノルズ数\(Re_{T}\)以上になっているはずです。

（オリフィス板を挿入するような条件では、限界レイノルズ数以上になっている可能性が高いです。）

流量\( Q\)の算出手順

下記の手順で流量\(Q\)を求めることができます。

オリフィス孔径\(D_{0}\)の設計手順

下記の手順でオリフィス孔径\(D_{0}\)を求めることができます。

計算例

それでは、具体的な計算例を通して、理解を深めていきましょう。

計算例①　オリフィスの流量計算

①　配管径\(D_{1}\)とオリフィス孔径\(D_{0}\)を調査する。

　計算前提より、配管径は\(D_{1}=0.080\) m、オリフィス孔径は\(D_{0}=0.020\) m

　ここで、オリフィス孔の断面積\(A_{0}\)をもとめておきます。

$$\begin{aligned}A_{0}&=\dfrac{\pi }{4}D_{0}^{2}\\[5pt]
&= \dfrac{\pi }{4}\times \left( 0.020\right) ^{2}\\[5pt]
&=0.00031\ \textrm{m²}\end{aligned}$$

②　流量\(Q\)を仮定する。

　\(Q = 17.9\) m³/hと仮定します。（\(Q = 0.0050\) m³/s）

③　オリフィス前後の差圧 \(\Delta P\)を計算する。

$$\Delta P=P_{1}-P_{2}=350\ \textrm{kPa}$$

④　開孔比\(m\)を算出する。　

$$\begin{aligned}m&=\left( \dfrac{D_{0}}{D_{1}}\right) ^{2}\\[5pt]
&= \left( \dfrac{0.020}{0.080}\right) ^{2}\\[5pt]
&= 0.0625\end{aligned}$$

⑤　(2)式から流量係数\(C\)を算出する。

⑥　(1)式に流量係数\(C\)を代入して、流量\(Q\)を求める。

$$\begin{aligned}Q&=CA_{0}\sqrt{\dfrac{2\Delta P}{\rho }}\\[5pt]
&=0.60\times 0.00031\times \sqrt{\dfrac{2\times 350\times 10^{3}}{1000}}\\[5pt]
&=0.0050\ \textrm{m³/s}\end{aligned}$$

⑦　仮定した流量\(Q\)と一致するまで試行錯誤する。

　今回の計算では、仮定した流量と計算結果の流量が一致したので、試行錯誤は不要です。

　実際の計算では、Excelのゴールシーク機能を使って、流量\(Q\)を探索します。

　参考記事　Excelゴールシークの使い方

⑧レイノルズ数\(Re\)を求める。

　まず、配管断面積\(A_{1}\)をもとめます。

$$\begin{aligned}A_{1}&=\dfrac{\pi }{4}D_{1}^{2}\\[5pt]
&=\dfrac{\pi }{4}\times \left( 0.080\right) ^{2}\\[5pt]
&=0.0050\ \textrm{m²}\end{aligned}$$

　次に、配管流速\(u_{1}\)をもとめます。

$$\begin{aligned}u_{1}&=\dfrac{Q}{A_{1}}\\[5pt]
&=\dfrac{0.0050}{0.0050}\\[5pt]
&=1.0\ \textrm{m/s}\end{aligned}$$

　よって、配管流速\(u_{1}\)を用いてレイノルズ数\(Re\)をもとめることができます。

$$\begin{aligned}Re&=\dfrac{D_{1}u_{1}\rho}{\mu }\\[5pt]
&=\dfrac{0.080\times 1.0\times 1000}{1.0\times 10^{-3}}\\[5pt]
&=7.9\times 10^{4}\end{aligned}$$

⑨　⑧で算出したレイノルズ数\(Re\)が、限界レイノルズ数\(Re_{T}\)以上であることを確認する。

　限界レイノルズ数\(Re_{T}\)をもとめます。

$$\begin{aligned}Re_{T}&=10^{4.185+2.831m-1.438m^{2}}\\[5pt]
&=10^{4.185+2.831\times 0.0625-1.438\times 0.0625^{2}}\\[5pt]
&=2.3\times 10^{4}\end{aligned}$$

よって、

$$Re >Re_{T}$$

となることから、(2)式の適用範囲であり、計算結果は妥当であることがわかりました。

今回は簡便のため、配管の圧力損失を無視できると仮定しましたが、実際の設計では無視できない場合もあります。

配管の圧力損失計算については、下の記事を参考にしてください。

計算例②　オリフィス孔径の設計

①　必要流量\(Q\)を設定する。

　今回、必要流量を\(Q = 100\) m³/hと設定します。（\(Q = 0.028\) m³/s）

②　配管径\(D_{1}\)を調査し、オリフィス孔径\(D_{0}\)を仮定する。

　計算前提より、配管径は\(D_{1}=0.15\) mで、

　オリフィス孔径は、\(D_{0}=0.050\) mと仮定します。

　ここで、オリフィス孔の断面積\(A_{0}\)をもとめておきます。

$$\begin{aligned}A_{0}&=\dfrac{\pi }{4}D_{0}^{2}\\[5pt]
&= \dfrac{\pi }{4}\times \left( 0.050\right) ^{2}\\[5pt]
&=0.00196\ \textrm{m²}\end{aligned}$$

③　オリフィス前後の差圧 \(\Delta P\)を計算する。

$$\Delta P=P_{1}-P_{2}=275\ \textrm{kPa}$$

④　開孔比\(m\)を算出する。　

$$\begin{aligned}m&=\left( \dfrac{D_{0}}{D_{1}}\right) ^{2}\\[5pt]
&= \left( \dfrac{0.050}{0.15}\right) ^{2}\\[5pt]
&= 0.111\end{aligned}$$

⑤　(2)式から流量係数\(C\)を算出する。

⑥　(1)式に流量係数\(C\)を代入して、流量\(Q\)を求める。

$$\begin{aligned}Q&=CA_{0}\sqrt{\dfrac{2\Delta P}{\rho }}\\[5pt]
&=0.60\times 0.00196\times \sqrt{\dfrac{2\times 275\times 10^{3}}{1000}}\\[5pt]
&=0.028\ \textrm{m³/s}\end{aligned}$$

⑦　仮定した流量\(Q\)と一致するまで試行錯誤する。

　今回の計算では、仮定した流量と計算結果の流量が一致したので、試行錯誤は不要です。

　実際の計算では、Excelのゴールシーク機能を使って、最適なオリフィス孔径を探索します。

　参考記事　Excelゴールシークの使い方

⑧レイノルズ数\(Re\)を求める。

　まず、配管断面積\(A_{1}\)をもとめます。

$$\begin{aligned}A_{1}&=\dfrac{\pi }{4}D_{1}^{2}\\[5pt]
&=\dfrac{\pi }{4}\times \left( 0.15\right) ^{2}\\[5pt]
&=0.018\ \textrm{m²}\end{aligned}$$

　次に、配管流速\(u_{1}\)をもとめます。

$$\begin{aligned}u_{1}&=\dfrac{Q}{A_{1}}\\[5pt]
&=\dfrac{0.028}{0.018}\\[5pt]
&=1.6\ \textrm{m/s}\end{aligned}$$

　よって、配管流速\(u_{1}\)を用いてレイノルズ数\(Re\)をもとめることができます。

$$\begin{aligned}Re&=\dfrac{D_{1}u_{1}\rho}{\mu }\\[5pt]
&=\dfrac{0.15\times 1.6\times 1000}{1.0\times 10^{-3}}\\[5pt]
&=2.4\times 10^{5}\end{aligned}$$

⑨　⑧で算出したレイノルズ数\(Re\)が、限界レイノルズ数\(Re_{T}\)以上であることを確認する。

　限界レイノルズ数\(Re_{T}\)をもとめます。

$$\begin{aligned}Re_{T}&=10^{4.185+2.831m-1.438m^{2}}\\[5pt]
&=10^{4.185+2.831\times 0.111-1.438\times 0.111^{2}}\\[5pt]
&=3.0\times 10^{4}\end{aligned}$$

よって、

$$Re >Re_{T}$$

となることから、(2)式の適用範囲であり、計算結果は妥当であることがわかりました。

(2)式の適用範囲外であった場合は、計算でもとめたオリフィス孔径の前後数mmずらした予備のオリフィス板を作成しておくとよいです。

参考文献

1. 化学工学便覧（改訂７版）（改訂６版PDF版P.324）
2. 絵とき「ポンプ」基礎のきそ-選定・運転・保守点検- 外山 幸雄 (著)P.105~108
3. はじめての化学工学 プロセスから学ぶ基礎 　化学工学会高等教育委員会 (編集) P.97~100