どうも。こんにちは。
ケミカルエンジニアのこーしです。
本日は、統計検定1級の勉強方法について、合格体験談を交えてお話しします。
2022年度は、統計応用(理工学)合格、統計数理は不合格という結果でした。
しかし、2023年度では、統計数理を合格しリベンジを果たすことができました。
この2年間、多くの教科書や過去問に取り組むことで、効果的な勉強方法がわかりました。
そこで本記事では、統計検定1級の勉強方法と合格への道のりを公開しますので、ぜひ読んでみてください!
私は、まったくの初心者から統計学の勉強を始め、統計検定2級、準1級、そして1級と、一歩一歩確実にスキルアップしてきました。
よって、これから統計学の勉強を始める方にも参考になると思います。
本記事の内容
・勉強時間
・理想の勉強方法
・勉強メモ
・まとめ
この記事を書いた人
 こーし(@mimikousi)
こーし(@mimikousi)
目次
統計検定1級の勉強方法(まとめ)

先に、まとめを書いておきます。
まとめ
- 統計数理対策は、現代数理統計学の基礎(久保川著)がオススメ
- 統計応用(理工学)対策は、統計検定1級 公式テキストと統計学実践ワークブック(準1級対応)の2冊で十分
- 公式問題集(過去問)は、6年分以上を3周回そう
- 勉強時間の目安は、300時間!!
- 良質なブログがたくさんあるので、わからない問題(式変形)は検索してみよう!
おすすめの参考書については、下記記事にまとめています。
-

-
【読み比べ】統計検定1級のおすすめ参考書
続きを見る
-

-
【統計検定1級】現代数理統計学 v.s 現代数理統計学の基礎
続きを見る
以下、具体的な勉強方法について書いていきますので、ぜひ読んでみてください。
実際にやった勉強
実際にやった、統計検定1級の勉強方法を紹介します。
使った参考書
参考書は、下記5つをメインに勉強しました。
取り組んだ時間を書籍名の右に書いています。
使った参考書
- 数理統計学(黒木著) 56時間
- 現代数理統計学(竹村著) 63時間
- 現代数理統計学の基礎(久保川著)2周目 13時間
- 統計検定1級対応 統計学(公式テキスト) 15時間
- 統計検定1級 公式問題集(過去問) 3冊 58時間
前回の挑戦では「現代数理統計学の基礎(久保川著)」で勉強したのですが、難しくて理解できていない気がしたので、今回は「数理統計学(黒木著)」「現代数理統計学(竹村著)」の2冊に挑戦してみました。
しかし、統計検定1級の出題範囲はどの教科書を読んでも難しく、結局、過去問を解きながら「現代数理統計学の基礎(久保川著)」を参照することが多かったです。
「現代数理統計学の基礎(久保川著)」は、カバー範囲が広く、かつ「定義、命題、補題、例」のように整理して記載しているため、復習しやすくとても重宝しました。
統計検定1級対策では、現代数理統計学の基礎(久保川著)が一番オススメですね。
公式テキストは、試験範囲を把握するためにしばしば参照しました。
限られたページ数で試験範囲を網羅するように書かれており、初心者がこの本だけで勉強するのは難しいかもしれません。
「現代数理統計学の基礎(久保川著)」で勉強した後、試験範囲が理解できているかを確認するために読むと良いと思います。
私は、各章の「練習問題」や「チェックシート」を主に活用しました。
ただ、統計検定1級の試験範囲を網羅している教科書は無いので、公式テキストを持っていると安心です。
最後の仕上げは、もちろん公式問題集(過去問)です。
過去問を解いているうちに、徐々に理解が深まった感じがします。
過去問をたくさん解くことが特に重要ですね!
公式問題集3冊(6年分)を2〜3周解きました。
勉強時間(2023年)
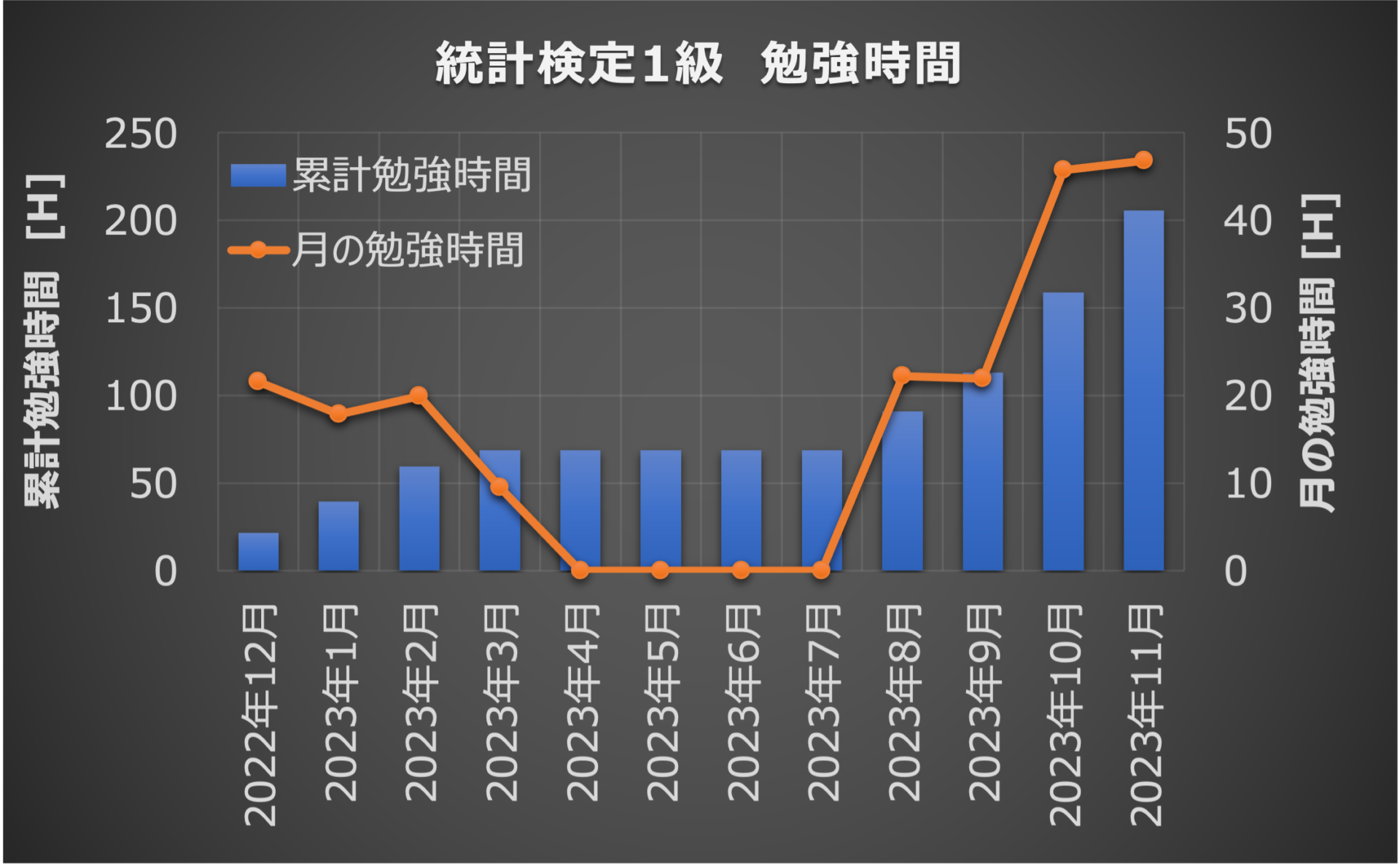
参考書別の勉強時間は前述しましたが、月別の勉強時間を下図に示します。
昨年度の試験終了後(12〜3月)は、反省として「数理統計学(黒木著)」を読みました。
その後、Pythonや実務向けの勉強に切り替えていましたが、再度8月から勉強を再開し、計200時間ほど勉強しました。
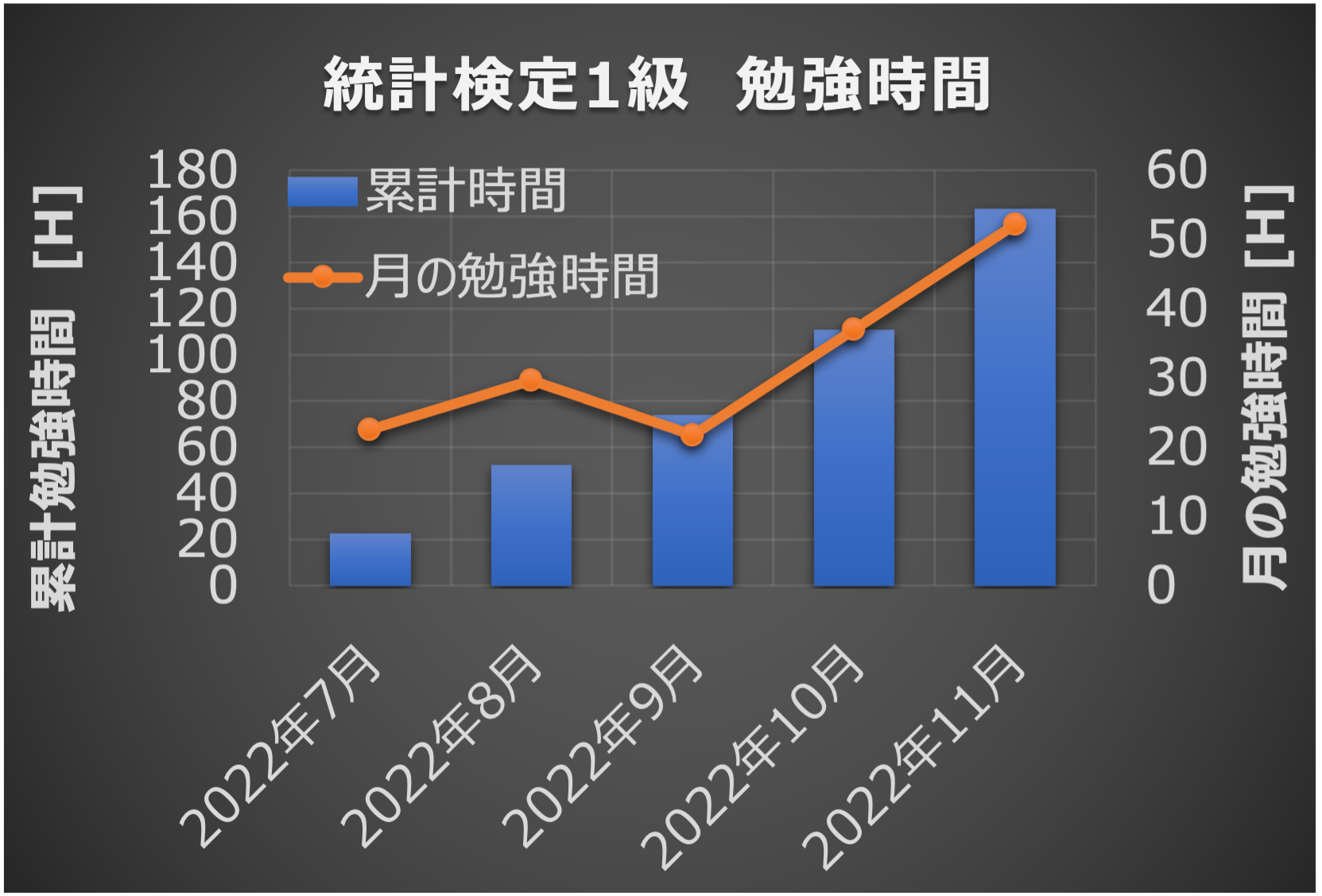
勉強時間(2022年)
ちなみに、前回の挑戦では計160時間ほど勉強しました。
よって、統計検定1級対策で計360時間ほど勉強したことになります。
2023年4〜7月は、統計検定の勉強をしていなかったため、期間が空いてしまい復習に時間を取られましたが、短期集中であればもう少し勉強時間は短くできたと思います。
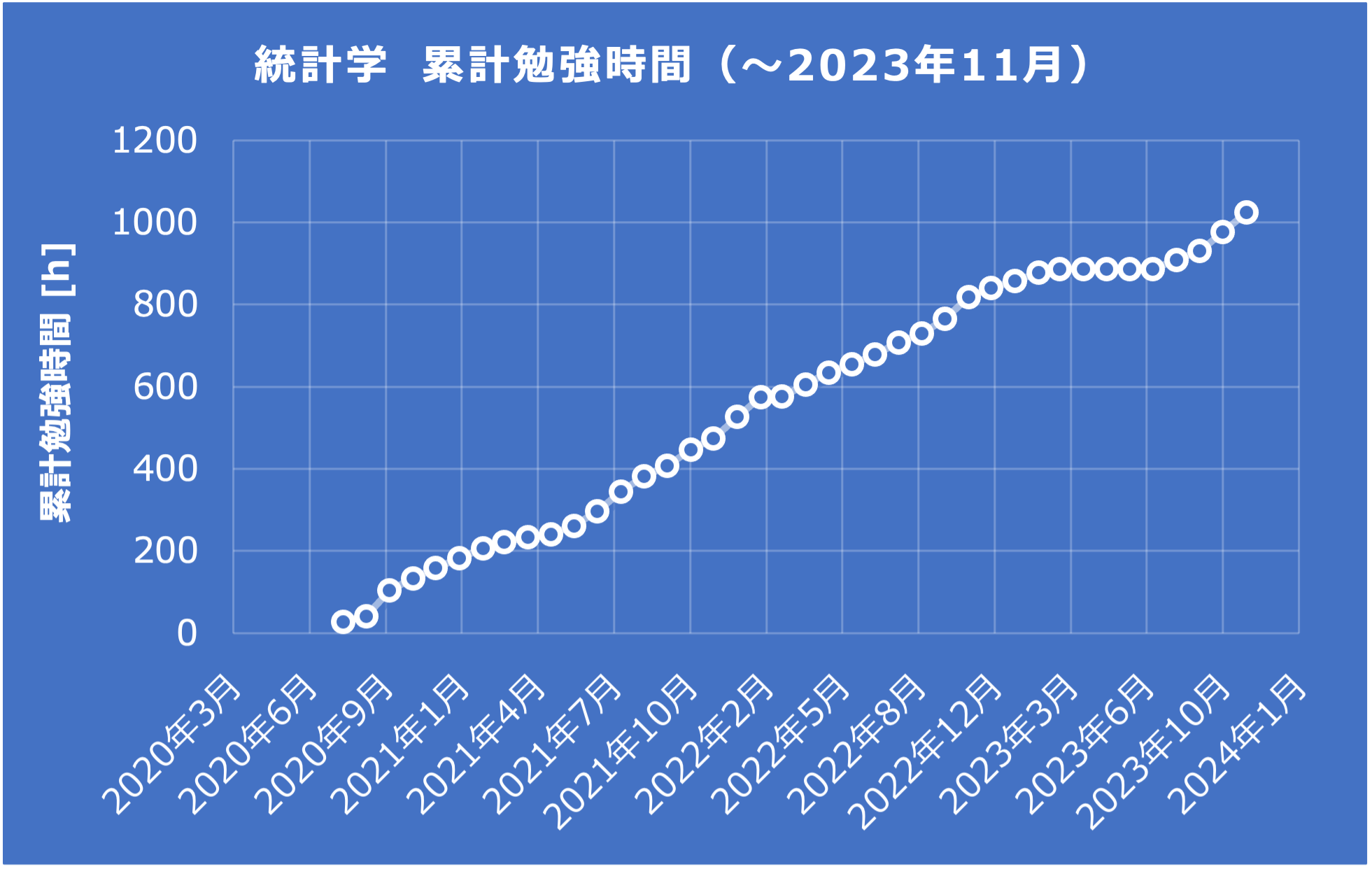
統計学の累計勉強時間
私は、2020年8月から統計学の勉強を始め、統計検定2級、準1級、1級と順番にスキルアップしてきました。
そこで、これまでの累計勉強時間を下図に示してみました。
統計検定1級の受験前にちょうど累計1,000時間を達成していました!
これまでの勉強内容については、前回の不合格体験談に詳しく書いているので、気になる方はぜひ読んでみてください。
-

-
【不合格体験談】統計検定1級の難易度は?
続きを見る
理想の勉強方法
これまでの2年間、たくさんの教科書を読み、過去問も6年分解いてきた経験から理想の勉強方法が定まってきたと感じています。
最初にお伝えしたいことは、資格試験対策の王道は「過去問をたくさん解くこと」です。
多くの教科書や参考書を読むより、過去問をたくさん解いたことで実力がついたという実感があります。
3年分では足りず、できれば6年分は解いた方が色んなパターンに慣れることができます。
また、1周目で理解して解くことは難しいので、3周くらい回すと良いと思います。
理想の勉強方法
●Step1 統計数理対策【目安:50時間】
まず、現代数理統計学の基礎(久保川著) を通読しましょう。
色んな教科書を読んでみて、一番オススメの教科書です。
●Step2 統計応用対策【目安:25時間】
統計検定1級 公式テキストと統計学実践ワークブック(準1級対応)の2冊で統計応用の出題範囲を網羅します。
必要なところだけ、ピックアップして読みましょう!
ちなみに、「理工学分野」は統計数理が理解できていれば、特別な対策はしなくても十分合格できます(私がそうでした)。
●Step3 過去問6年分(以上)を1周解く【目安:100時間】
●Step4 教科書の復習【目安:25時間】
現代数理統計学の基礎(久保川著) の2周目をやります。
あと、統計検定1級 公式テキストと統計学実践ワークブック(準1級対応)の練習問題を解いてみましょう。
●Step5 過去問をひたすら回していく【目安:100時間】
できれば3周はやりましょう。
過去問解きながら、教科書や良質なブログを参照し、理解を深めましょう!
勉強時間の目安は300時間です。
社会人の方は1日の勉強時間が限られてしまうので、少なくとも試験(11月末)半年前の6月頃から対策する必要があると思います。
もし、現代数理統計学の基礎(久保川著) を読んで全然歯が立たないなと思ったら、数理統計学(黒木著)を読んでみましょう。
内容が易しい教科書は、解説も簡素になってしまいますが、黒木先生の「数理統計学」は解説が超詳しいです。
よって、「現代数理統計学の基礎」が難し過ぎる方には、黒木先生の「数理統計学」をオススメします。
統計検定1級勉強メモ
ここで、勉強しながら得た気づきをつぶやいたポスト(ツイート)を紹介します。
✅統計検定1級
過去問を解いてみたけど、数学力でつまずくことが多い。
ただ、良質な解説を載せてるブログが多くてとても助かる。
・あつまれ統計の森
・SATOLOG
・有意に無意味な話
・DataArts
・脳内ライブラリアン
など
公式問題集の解説が難しくて理解できなかったら、すぐネットで検索すべきだな— こーし⚡️ケミカルエンジニア (@mimikousi) August 30, 2022
教科書や参考書の証明を追っているときや、過去問を解いているときに、解説が理解できず止まってしまうことが多々あります。
教科書の解説や、過去問解答の解き方が理解できないときは、良質なブログを参考にしましょう。
私は何度も、ブログに助けてもらいました。
✅デルタ法(Delta method)
統計検定1級の過去問に出題されていたので、何冊か教科書を読んでみたが全然理解できず。。
そこで、ネット検索してみたら天才的なわかりやすさで、ものの数分で理解できてしまった(笑)
ブログってすごいなと思った!【参考】知識のサラダボウルhttps://t.co/FYa3HSKLZ4
— こーし⚡️ケミカルエンジニア (@mimikousi) November 10, 2022
過去問でデルタ法が出てくるのですが、下記のブログを読んで理解できました。
また、3変量正規分布の条件付き期待値と分散は、下記記事を参考にしました。
最後に、過去問6年分を解いた際のメモを下記にまとめました。
参考記事や教科書の該当ページをまとめているので、ぜひ参考にしてみてください。
✅統計検定1級 統計数理(2016年)
問1 正規分布
[1]最尤推定量
[2]バイアス、不偏推定量
[3]平均2乗誤差(MSE)
[4]クラメール・ラオの不等式問2 指数分布
[1]期待値
[2]上側確率
[3]最尤推定量、不偏推定量
[4]確率変数の和
モーメント母関数
【参考】DataArtshttps://t.co/4h3PWLMvJ6問3…
— こーし⚡️ケミカルエンジニア (@mimikousi) November 17, 2023
✅統計検定1級 統計数理(2017年)
問1 歪度、尖度
[1]標本平均の期待値と分散、不偏推定量
※良く出るので覚える(久保川本P.86)
[2][3][4]歪度と尖度
[5]最尤推定量問2 一様分布、順序統計量
[1]最尤推定量
久保川本P.141問4
竹村本P.143
[2]不偏推定量
[3]Xmaxの確率密度関数…— こーし⚡️ケミカルエンジニア (@mimikousi) November 17, 2023
✅統計検定1級過去問(2018年)
問1 カイ二乗分布
[1]不偏分散
現代数理統計学の基礎(久保川著)P.86参照
[2][3]カイ二乗分布の期待値と分散
ガンマ関数の性質をフル活用
統計検定1級公式テキストP.39の(2.2.5)式が使える
[4]デルタ法
知識のサラダボウル参照https://t.co/FYa3HSKLZ4 pic.twitter.com/qt5oxcWW22— こーし⚡️ケミカルエンジニア (@mimikousi) October 16, 2023
✅統計検定1級過去問(2019年)
問1 二項分布、確率母関数
[1]確率母関数
[2]二項分布の期待値と分散
※ポイントは、二項定理を覚えておくこと
久保川本P.30〜33
[3][4]確率母関数と累積分布関数の不等式問2 指数分布
[1]指数分布の期待値
[2]たたみ込み
[3][4]リスク関数…— こーし⚡️ケミカルエンジニア (@mimikousi) October 21, 2023
✅統計検定1級過去問(2021年)
問1 指数分布、一様分布
[1][2]期待値
[3]たたみ込み
※積分する範囲に注意
久保川本P.71〜73
明解演習 数理統計P.42
[4]変数変換(確率積分変換)
※一様分布f(y)の累積分布関数が、F(y)=yとなることに着目
久保川本P.24問2 超幾何分布、ベイズ法…
— こーし⚡️ケミカルエンジニア (@mimikousi) October 27, 2023
✅統計検定1級過去問(2022年)
問1 確率の計算
[1][4]独立事象
[2][3]独立とは限らないとき
過去の出題と大きく傾向が異なるので注意。。
ベン図を書いて考える。問2 一様分布、条件付き同時確率分布
[1]周辺累積分布関数
[2]独立の定義
[3][4]確率の計算
久保川本P.69〜71(変数変換)…— こーし⚡️ケミカルエンジニア (@mimikousi) November 3, 2023










