
わかりやすく解説するのでしっかり勉強していこう。

どうも。こんにちは。ケミカルエンジニアのこーしです。
本日は、「サンプルサイズの決め方①(平均値の差の検定)」について、わかりやすく解説します。
この記事を読めば、平均値の差の検定(t検定)のような仮説検定を行う際に、どのくらいのサンプル数が必要なのかわかるようになります。
t検定の具体的な手順については、下記の記事で解説しています。
-

-
【例題でわかる】現場で使えるt検定!
続きを見る
本記事の内容
- 必要となるサンプル数
- 仮説検定とは
- 仮説検定の手順
- 第1種の誤りと第2種の誤り
- 検定力(検出力)
- 検定力の求め方
- 参考文献
この記事を書いた人
 こーし(@mimikousi)
こーし(@mimikousi)
サンプルサイズの決め方(平均値の差の検定)
仮説検定の代表例である「独立な2群の平均値の差の検定(t検定)」に対して、必要なサンプルサイズを計算してみます。
計算前提は下記の通りです。
計算前提
- 比較する2群のデータは独立(2群のデータに相関がない)
- 帰無仮説は「2群の平均値に差は無い(\(\overline{y}_{1} - \overline{y}_{2} = 0\))」
- 2群の母分散(標準偏差)は等しい(\(\sigma_1 = \sigma_2 \))
- データ数は、2群ともに等しい(\(n_1 = n_2\))
- 有意水準\(\alpha = 0.05\)
- 両側検定
上記条件で算出した各群の必要サンプル数(データ数)を図示しました。
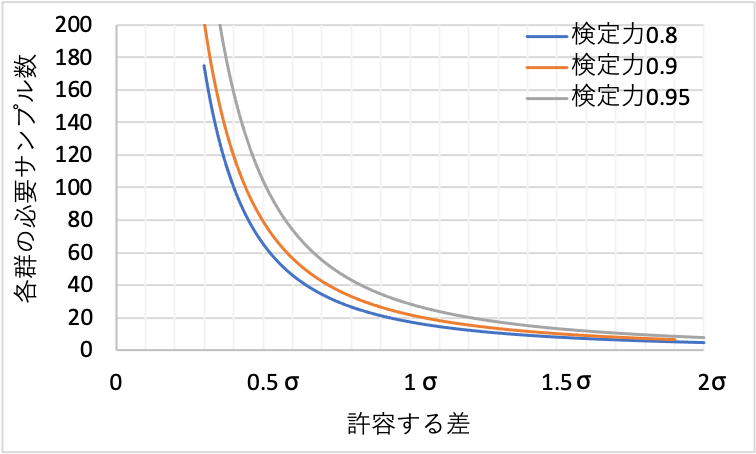
上のグラフを参考に、サンプルサイズの設計を行うことができます。
例えば、2群平均値の差を1σの差まで95%検出したい場合(検定力0.95)、必要となるサンプル数は30くらいです。(検定力については後ほど解説します)
0.5σまで検出したいとなると、検定力0.95では、必要となるサンプル数は100を超えます。
また、サンプル数が1桁の場合、2σより小さい差を検出することは困難であることが分かります。
つまり、サンプル数が極端に少ないとき、本当は差があったとしても、2σより小さい差は、「差が無い」という検定結果となる可能性が高くなります。(第2種の誤りのことです。後述します)
導出過程も知りたい方はサンプルサイズの決め方(永田著)を参考にしてみて下さい。(結構難しいです)
どうやってサンプルサイズを計算するのか?
以下は、サンプルサイズの決め方の概念部分を解説していきます。
仮説検定とは?
仮説検定とは、「平均値の差」や「相関の有無」などを統計的に判断する方法のことです。
例えば、同じ機械・製法で作った製品のロット間の品質差を考えます。
当然、品質は同じになるはずですが、実際に測定してみると、平均値が「10」異なったとします。
この「10」という差が、誤差の範囲内なのか、何か意味のある差(有意差)なのかを判定することが仮説検定です。(有意差検定とも呼ばれます)
仮説検定の手順
- 仮説の設定
帰無仮説\(H_0\)と対立仮説\(H_1\)を設定 - 検定統計量(tなど)の算出
- 棄却域の設定
まず有意水準\(\alpha\)(基本5%)を決め、棄却域を求める - 判定
t分布表を読み取り、データから算出した検定統計量が、
・棄却域に入る → 帰無仮説を棄却
・棄却域に入らない → 帰無仮説を採択 - 結論
仮説検定の方法は、まず「帰無仮説」と「対立仮説」と呼ばれる仮説を立てます。
次に、その帰無仮説が正しいと仮定して検定統計量の分布(帰無分布)を算出します。
そして、対象データ(サンプル)から算出した検定統計量が、その帰無分布のどの位置に来るのかによって、帰無仮説が正しいのかどうかを判断します。
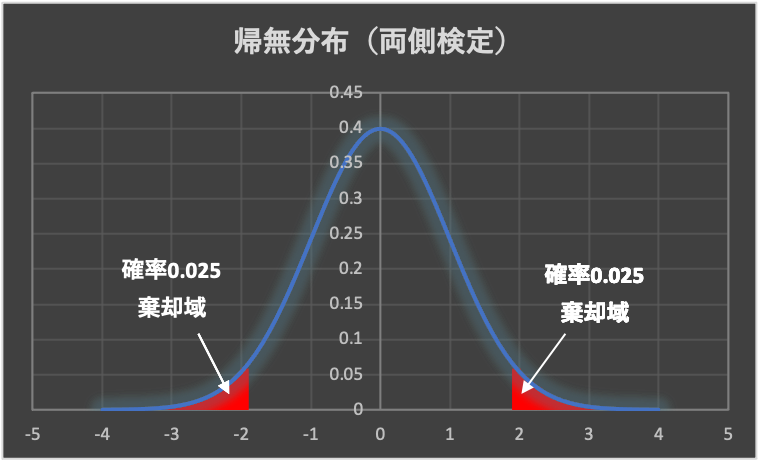
帰無仮説が正しいのかどうかを判断する基準のことを「有意水準(\(\alpha\))」と呼び、慣例的に5%(\(\alpha = 0.05\))を用います。
5%よりも小さい確率で起きるということは、帰無仮説のもとではめったに起こりえないということであり、帰無仮説は棄却(reject)されます。(帰無仮説が棄却されると、対立仮説が採択されます)
よって、帰無分布の有意水準\(\alpha\)以下の範囲を「棄却域」と言います。
一方、棄却域に入らなかった場合は、帰無仮説を「採択」します。
一般に、「平均値の差」や「相関の有無」を検定する場合は、帰無分布の両側に棄却域を設定する「両側検定」を行います。
一方、関心があるのが分布の片側のみの場合、棄却域を片側にのみ設定する「片側検定」を行います。
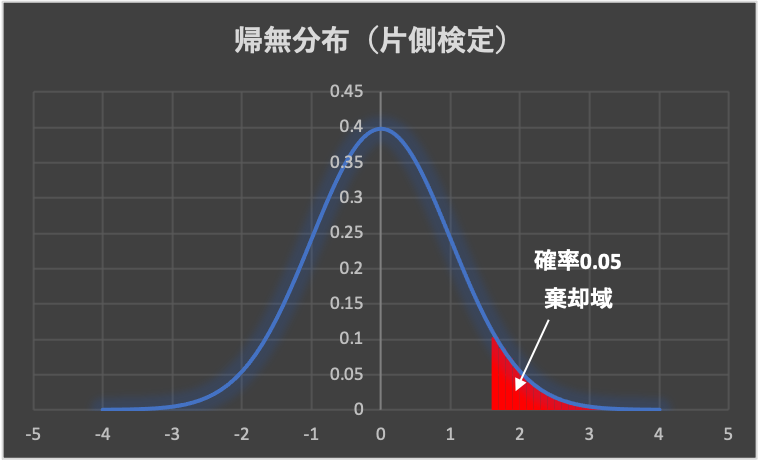
ちなみに、帰無仮説が採択された場合は、棄却した場合と異なり、仮説が「真」であることを積極的に証明した訳ではないので注意が必要です。
第1種の誤りと第2種の誤り
仮説検定において、下記2種類の誤りが考えられます。
2種類の誤り
①第1種の誤り:帰無仮説が正しいのに、それを棄却する
②第2種の誤り:帰無仮説が誤っているのに、帰無仮説を採択する
ここで、本当は帰無仮説が正しいのに、誤って棄却してしまう(第1種の誤りを犯す)可能性はどのくらいあるのでしょうか?(本当は差が無いのに、差があると判断してしまう)
答えは簡単です。
有意水準\(\alpha\)と同じ確率です。
有意水準\(\alpha\)を5%とすると、帰無仮説が正しいのに棄却してしまう確率は5%となります。
ここで、有意水準\(\alpha\)を5%ではなく、1%や0.1%と小さくしたら良いと思うかもしれません。
しかし、そうすると今度は、帰無仮説が誤っているのに帰無仮説を採択してしまう(第2種の誤りを犯す)確率が大きくなってしまいます。
下図を見てみましょう。
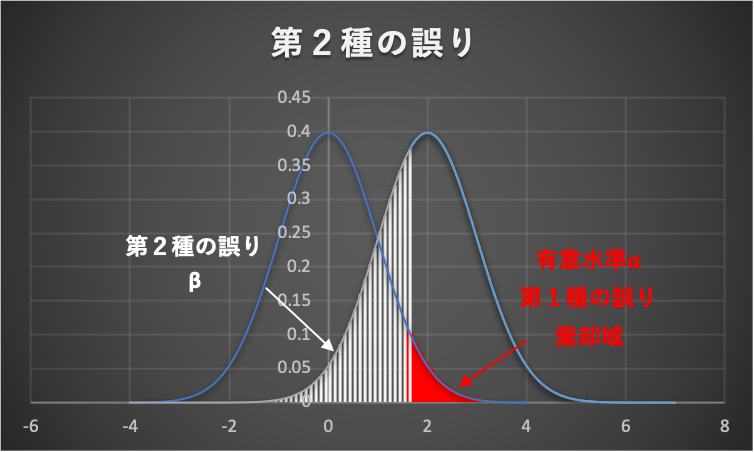
- 帰無仮説:平均値の差\(\mu = 0\)
- 片側検定
- 有意水準\(\alpha = 0.05\)
- 実際は、平均値の差\(\mu = 2\)
上の条件のように、もし帰無仮説が誤っていたら、サンプルデータは帰無分布と異なる分布に従います。
しかし、サンプルデータが帰無分布と異なる分布だったとしても、白のたて線部分のように、帰無分布の採択域(棄却域以外)に入ってしまう可能性(第2種の誤り\(\beta\))があります。
上図からもわかるように、第1種の誤り(有意水準\(\alpha\)を)を小さく設定すると、棄却域が右にずれて(狭くなって)、採択域が大きくなり、結果、第2種の誤りが起こる確率も大きくなります。
すなわち、第1種の誤り(\(\alpha\))と第2種の誤り(\(\beta\))はトレードオフの関係にあります。
よって、有意水準\(\alpha\)は、大きすぎず、小さすぎない\(\alpha =0.05\)が慣例的に選ばれています。
検定力(検出力)
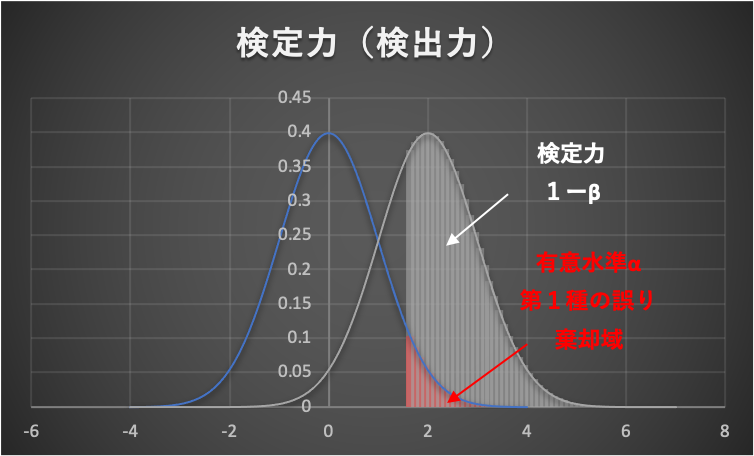
帰無仮説が正しくないときに、ちゃんと帰無仮説を棄却(有意な差があると判断)できる確率のことを「検定力(検出力)」と言います。
上図の例では、検定力は約60%程度であり、誤った仮説をちゃんと棄却できる確率が約60%くらいということです。
検定力を大きくする方法は、下記の2パターンです。
- サンプル数を増やして、
分布をシャープにする + 検定統計量tを大きくする(2つの分布を離す) - 検出する差(効果量\(\delta\))を大きく取る
よって、「平均値の差」をどのくらいの精度で正しく検出する必要があるのかを考え、検定力が十分高くなるようにサンプルサイズを決めます。
検定力の求め方
前半で述べた「独立な2群の平均値の差」の検定は、「t検定」と呼ばれ、検定統計量tがt分布に従います。
計算前提をもう一度書いておきます。
計算前提
- 比較する2群のデータは独立(2群のデータに相関がない)
- 帰無仮説は「2群の平均値に差は無い(\(\overline{y}_{1} - \overline{y}_{2} = 0\))」
- 2群の母分散(標準偏差)は等しい(\(\sigma_1 = \sigma_2 \))
- データ数は、2群ともに等しい(\(n_1 = n_2\))
- 有意水準\(\alpha = 0.05\)
- 両側検定
t検定における検定力の求め方は、下記の通りです。
(1)有意水準\(\alpha\)から棄却域を設定
有意水準\(\alpha = 0.05\)(両側検定なので、片側0.025ずつ)とサンプルサイズ(データ数)からt値(有意値)を算出し、棄却域を求めます。
まず、検定統計量tと母集団の標準偏差の推定量\(s^{\ast}\)を下記の通り定義します。
また、2群の平均値を\(\overline{y}_{1},\overline{y}_{2}\)とおきます。
$$\begin{aligned}t&=\frac{\overline{y}_{1}-\overline{y_{2}}}{s^{\ast }\sqrt{\frac{1}{n_{1}}+\frac{1}{n_{2}}}}\\[5pt]
&=\frac{\overline{y}_{1}-\overline{y}_{2}}{s^{\ast}}\sqrt{\frac{n_{1}n_{2}}{n_{1}+n_{2}}}\end{aligned}$$
$$s^{\ast }=\sqrt{\frac{(n_1-1)s_{1}^{2}+(n_{2}-1)s_2^{2}}{n_{1}+n_{2}-2}}$$
ちなみに、検定統計量tは下記のように分解して表すことができます。
検定統計量 t = 効果量\(\delta\) × サンプルサイズ
$$\delta =\frac{\overline{y_{1}}-\overline{y_{2}}}{s^{\ast }}$$
効果量\(\delta\)は、2群の平均値の差を標準偏差\(s^{\ast }\)で割っているので、「標準化された平均値差」を表しています。
つまり、平均値の差が標準偏差の何倍(何σ)あるかという指標です。(母集団の標準偏差\(\sigma\)の推定量が\(s^{\ast}\)ですので、\(\sigma = s^{\ast}\)です)
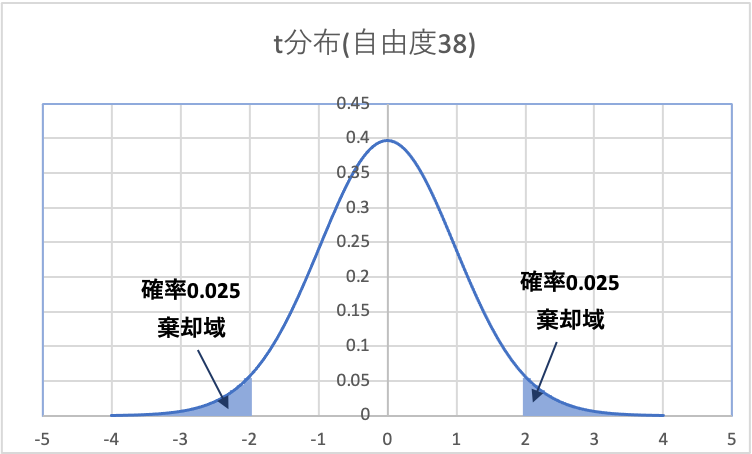
ここで、サンプルサイズを2群ともに\(n = 20\)として、t分布表から有意となるt値を求めると、
$$t_{0.025}( df=20+20-2= 38) =2.024$$
両側検定なので、片側0.025ずつの棄却域を設定します。
(2)検出したい差(何σか)を仮定して、検定統計量tを求める
仮に、検出したい差を0.5σとすると、効果量\(\delta =0.5\)となるので、サンプルの検定統計量tは下記のように求まります。
$$\begin{aligned}t&=0.5\times \sqrt{\frac{20\times 20}{20+20}}\\[5pt]
&=1.58\end{aligned}$$
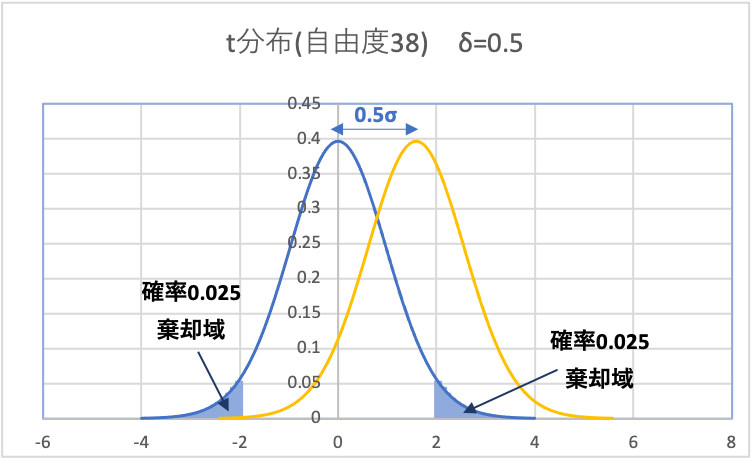
(3)(2)で得られた検定統計量tを中心とする非心t分布を書く
平均値の差が無いと仮定した帰無分布から、0.5σズレたときの分布を書きます。(非心t分布)
(4)非心t分布のもとで、tが棄却域に入る確率(検定力)を算出
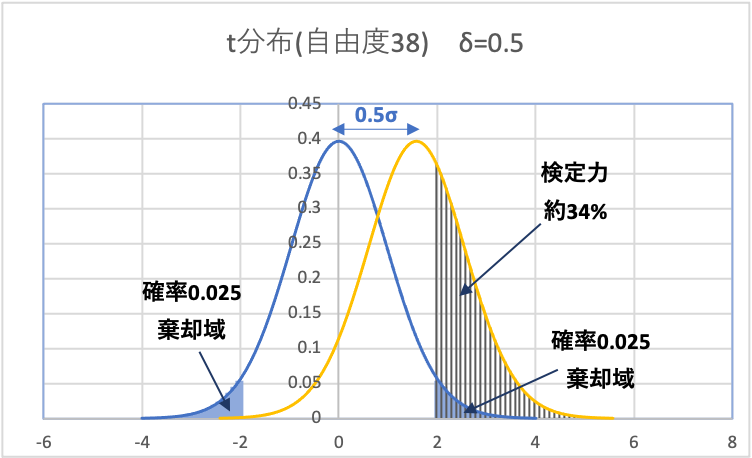
上図のように、非心t分布の中で、帰無分布の棄却域に重なる部分が検定力となります。
このようにして求めた検定力は、約34%となります。(結構低いですね)
ちなみに、検出したい差異を1σ(効果量\(\delta =1.0\))とすると、下図のようになり、検定力は約87%まで上昇します。
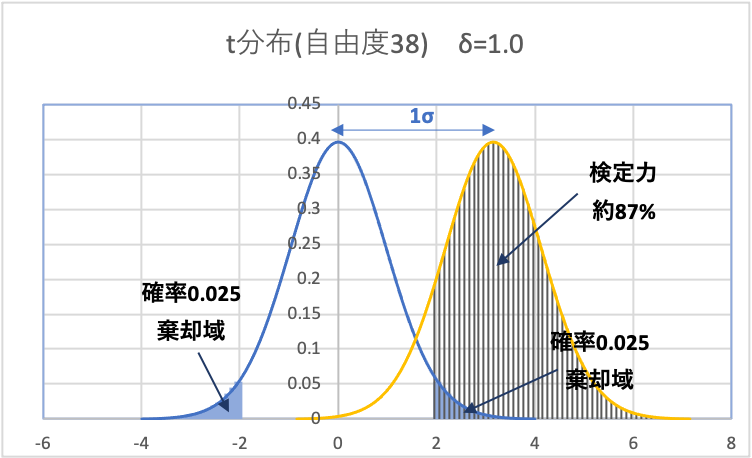
このように、「サンプルサイズ」と「検出したい差(何σか)」を様々に変更してそれぞれ検定力を求めることで、下図のような許容する差と必要となるサンプル数のグラフを作成することができます。(前半にある図と同じです)

参考文献
1.心理統計学の基礎(有斐閣アルマ) 統計検定2級〜準1級レベル
本記事では、この本を大いに参考にさせてもらいました。
初級から中級レベルに運んでくれるような、非常に詳しい解説があります。
対象は、統計検定2級レベル以上です。
-

-
【書評】心理統計学の基礎 難易度と読み方を解説!
続きを見る
2.統計学入門 東京大学出版会(通称赤本) 統計検定2級レベル
仮説検定について、コンパクトにわかりやすくまとまっています。
本質を突いた解説という感じです。
-

-
【書評】「統計学入門」(東京大学出版会)
続きを見る



