どうも、こんにちは。ケミカルエンジニアのこーしです。
本日は、ポンプのNPSHについてわかりやすく解説していきます。
この記事を読むことで、NPSHの意味を理解し、ポンプの設計ができるようになります。
また、キャビテーションを回避する運転方法を身につけることができます。
本記事の内容
・ポンプのNPSHとは
・NPSHの求め方
・現場で使えるNPSHの計算例
・キャビテーション対策
この記事を書いた人
こーし(@mimikousi)
目次
ポンプのNPSHとは？
NPSHは、ポンプが安全に運転できるかどうかを示す指標です。
言い換えますと、NPSHという指標を用いることで、ポンプがキャビテーションを起こすかどうかを判断することができます。
NPSHには、「ポンプ固有のNPSH」と「運転条件から求めたNPSH」の２種類あり、それらを比較することで、キャビテーションを起こすかどうかを判断します。
キャビテーションを起こさない条件 運転条件から求めたNPSH ＞ ポンプ固有のNPSH
・ポンプ固有のNPSH → NPSHr（NPSH3）
・運転条件から求めたNPSH → NPSHa
ちなみに、NPSHはNet Positive Suction Head（正味吸込ヘッド）の略です。
具体的な定義は下記の通りです。
NPSHr（NPSH required、NPSH3）
NPSHrは、「必要有効吸込ヘッド」と呼ばれます。
ポンプの羽根車（インペラ）や吸込口の設計により決まるポンプ固有のヘッドです。
ポンプが液を吸い込むために必要な全圧ヘッド（速度ヘッド＋圧力ヘッド）を表しています。
NPSHa（NPSH available)
NPSHaは、「有効吸込ヘッド」と呼ばれます。
ポンプ吸込口の液体が持つ全圧ヘッド（絶対圧基準）から、飽和蒸気圧ヘッドを差し引いたものです。
よって、吸込口における液体が飽和蒸気圧に対してどれだけ余裕をもっているかを表しています。
ここで、エネルギーを「長さの次元（m）」で表したものを「ヘッド」と呼びます。
圧力 [Pa]も密度\(\rho\)[kg/m³]と重力加速度\(g\)[m/s²]で割ると、ヘッド [m]に変換できます。
液体の圧力よりも飽和蒸気圧の方が高くなると、気泡が発生します。
ポンプ内で気泡が発生すると、ポンプはキャビテーションを起こします。
キャビテーションを起こしますと、ポンプに騒音と振動が生じ、ポンプが損傷したり、ひどい場合には送液できなくなります。
NPSHrとNPSHaを用いることで、キャビテーションを起こすことなく運転できる範囲を下記のように表すことができます。
$$NPSH_{a} >NPSH_{r}$$
実際の設計では、さらに下記のような関係を満たす必要があります。
$$NPSH_{a} >NPSH_{r}+1 $$
または、
$$NPSH_{a}>NPSH_{r}\times 1.3$$
飽和蒸気圧とは？
飽和蒸気圧とは、液体が蒸気（気体）になろうとする力のことです。
温度が高くなると、分子の運動が激しくなりますので、飽和蒸気圧は大きくなります。
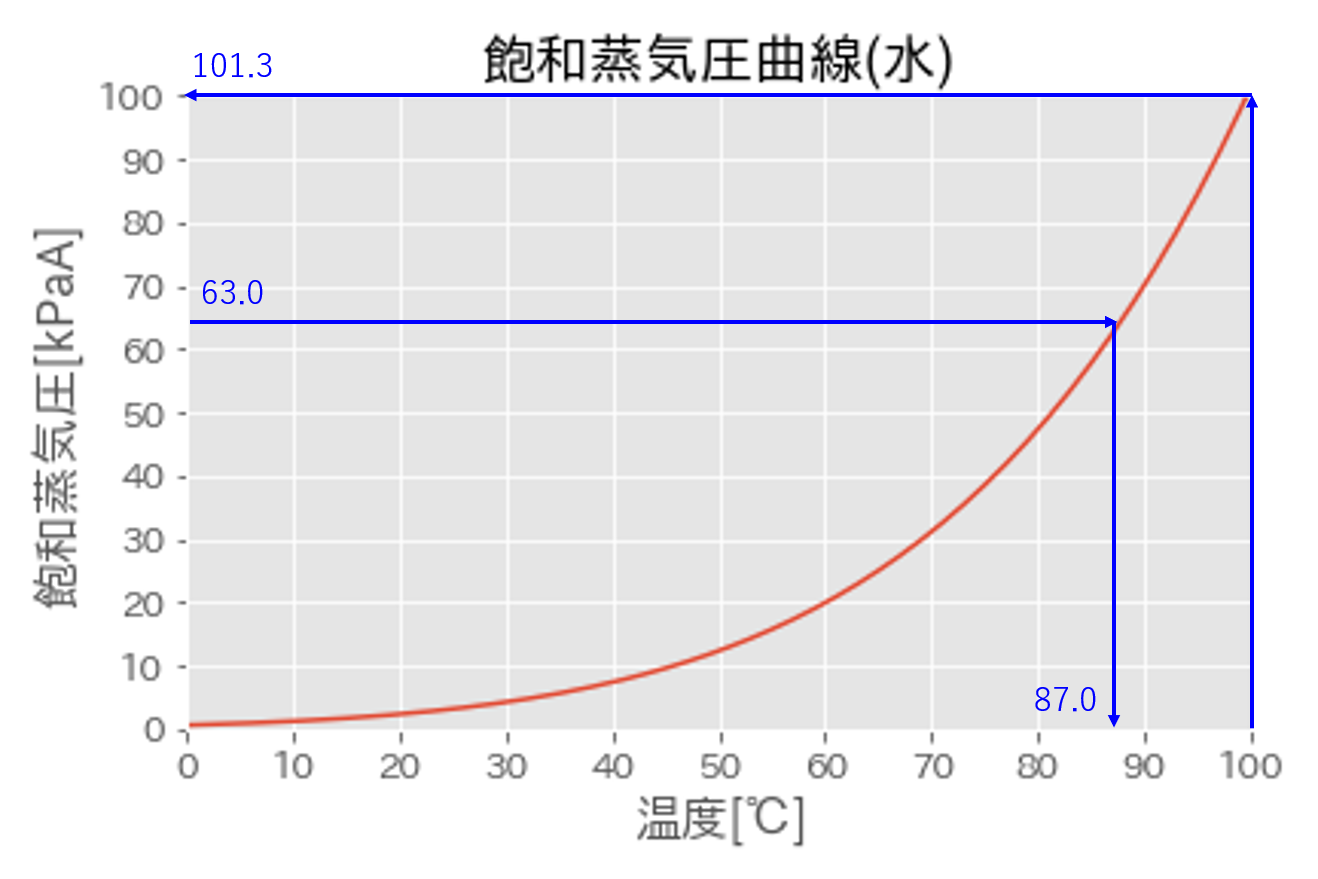
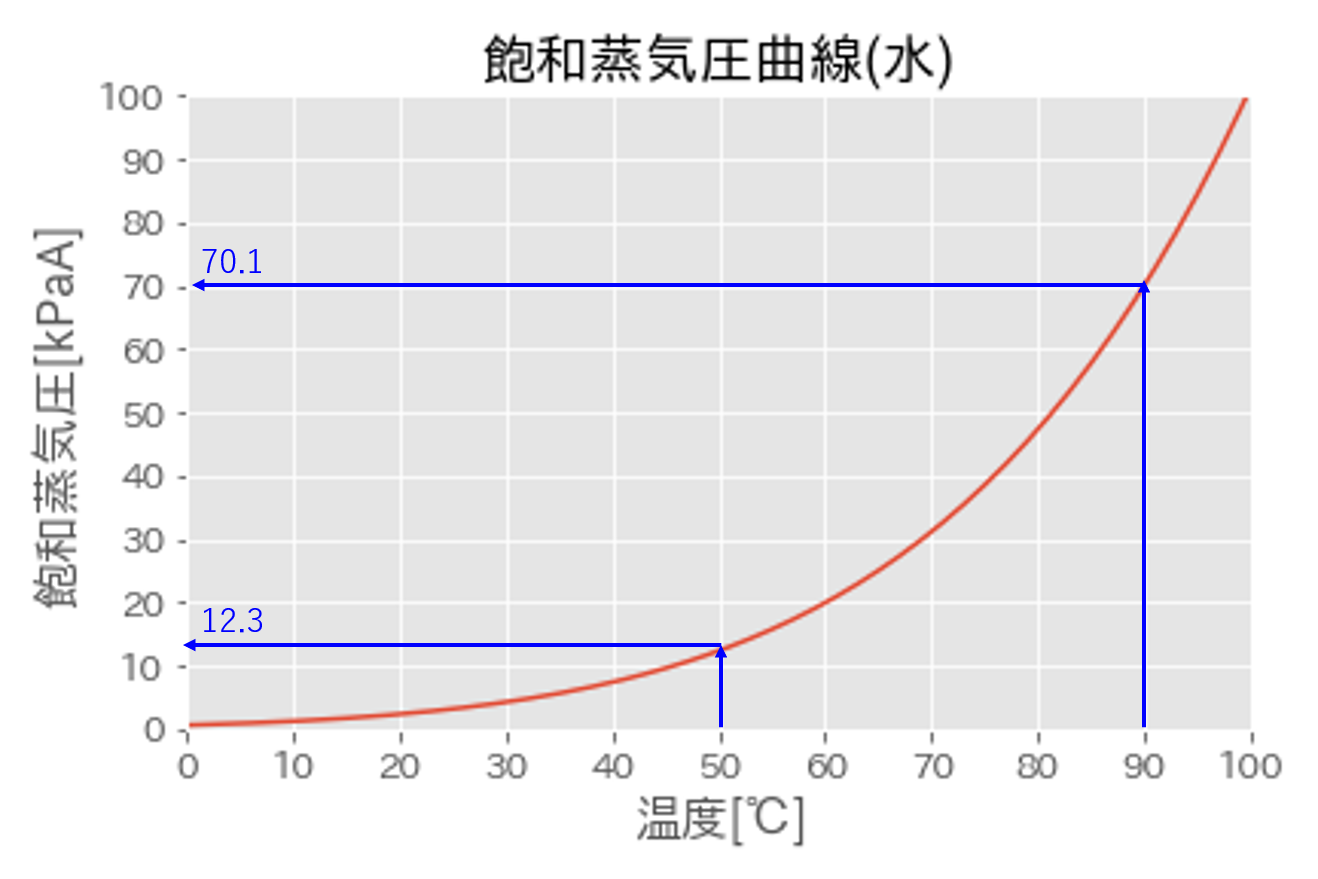
例えば、水は100℃で飽和蒸気圧が101.3 kPaA（大気圧）となり、沸騰します。
しかし、富士山の山頂では、気圧が低く、63 kPaA程度であるため、水は約87℃で沸騰します。
したがって、ポンプによる圧力損失により、液体の圧力が低下すると、気泡が発生しやすくなることがわかります。
-
-
蒸気圧とは？ 蒸気圧曲線から沸点と圧力の関係を解説！
続きを見る
キャビテーションとは？
ポンプの羽根車（インペラ）付近にて局部的な低圧域が生じ、液体が蒸発して気泡を生じることをキャビテーションといいます。
【参考】ポンプのキャビテーション|TLV
リンクの記事を読むためには、TLVの無料会員登録をする必要がありますが、登録しておくことをオススメします。
スチームトラップやウォーターハンマーなどの技術資料が豊富にあり、何度も参考にさせていただきました。
NPSHrの求め方
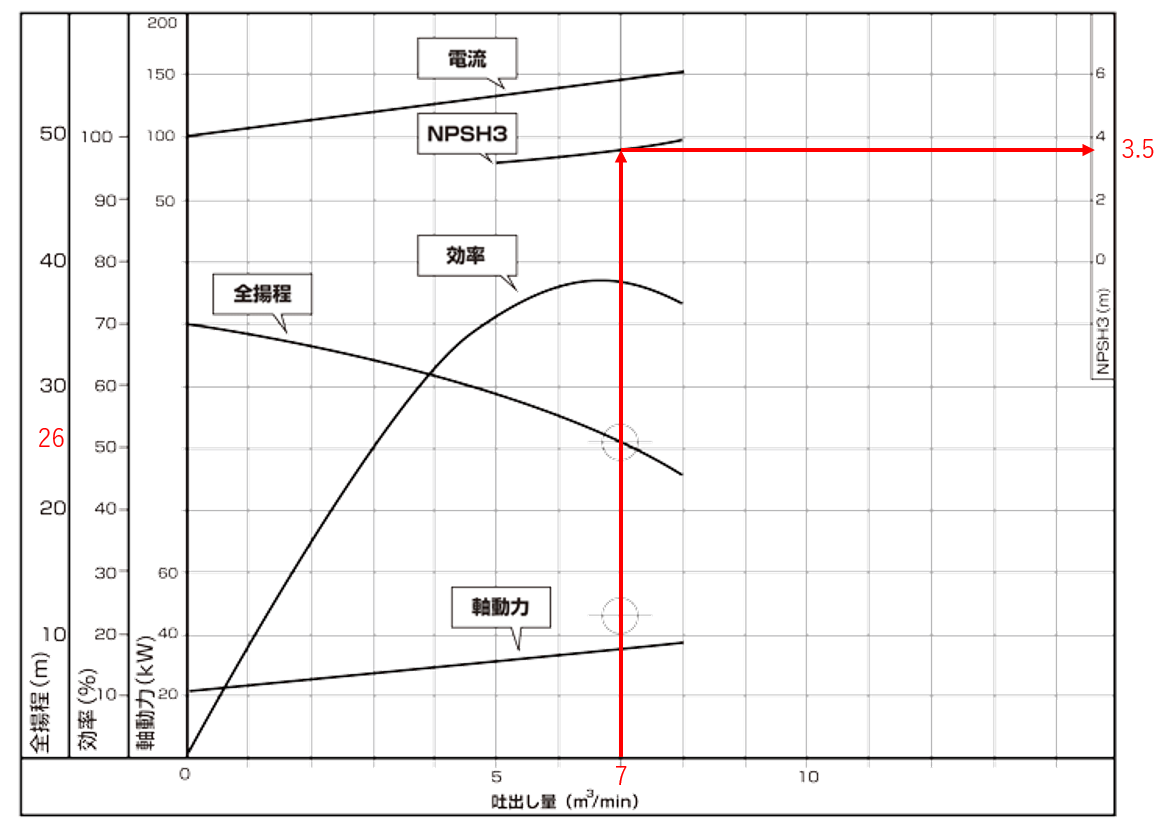モノタロウ 遠心ポンプの基礎講座 3-1ポンプの性能曲線の見方より引用
NPSHr（NPSH3）は、ポンプ固有のヘッドですので、ポンプの性能曲線を見ればわかります。
上図の性能曲線では、吐出し量が7 m3/minのとき、NPSHr（NPSH3）は、3.5 mであることがわかります。
また、NPSHr（NPSH3）は下記の（１）式で表すことができます。
\(N\) : 回転数 [rpm(=min¯¹)]
\(Q\): 吐出し量 [m³/min]
\(S\) : 吸込比速度 [-] → ほとんどの場合1200で一定。（ポンプの設計による）
（１）式からわかるように、NPSHr（NPSH3）は、下記のような性質をもつことがわかります。
- 回転速度が高くなると増大する。
- 吐出し量が増えると増大する。
したがって、NPSHr（NPSH3）は、ポンプの設計（吸込比速度、回転数）と吐出し量により決まるポンプ固有のヘッドということがわかります。
NPSHaの求め方
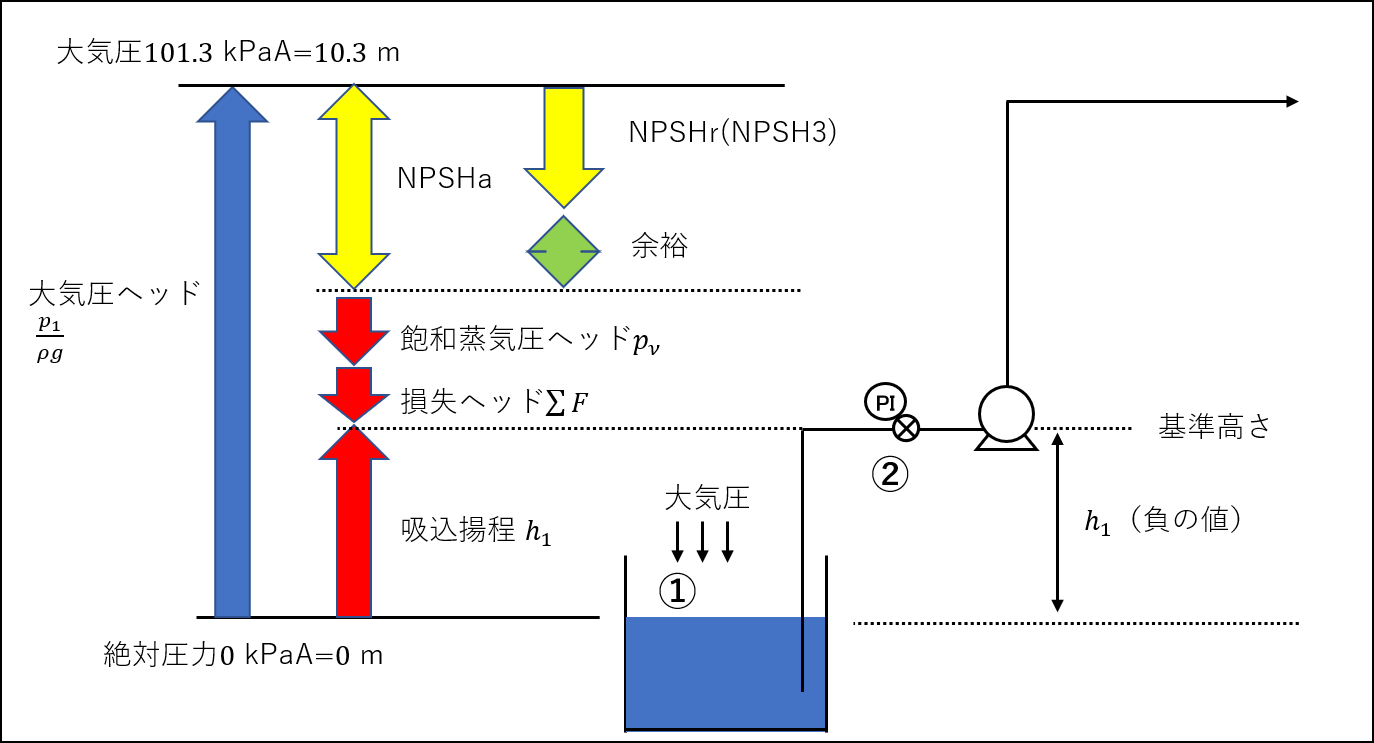
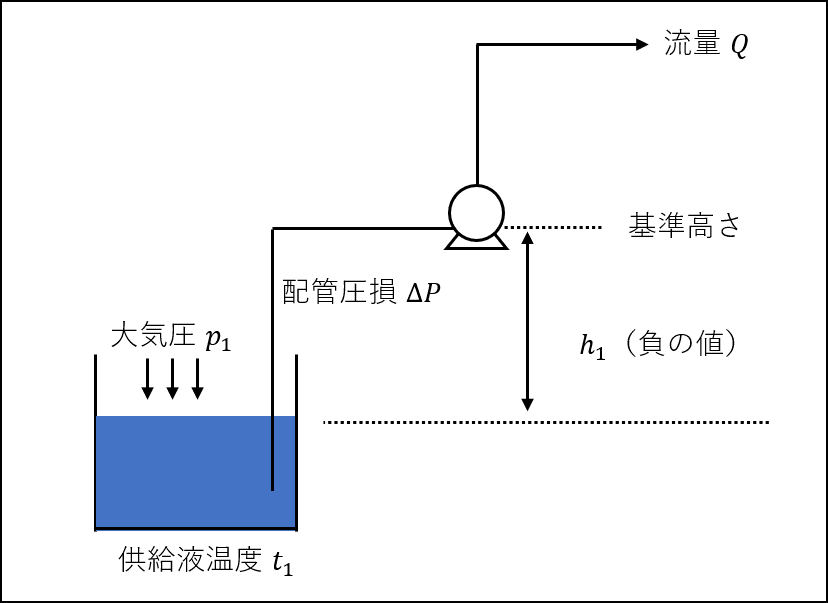
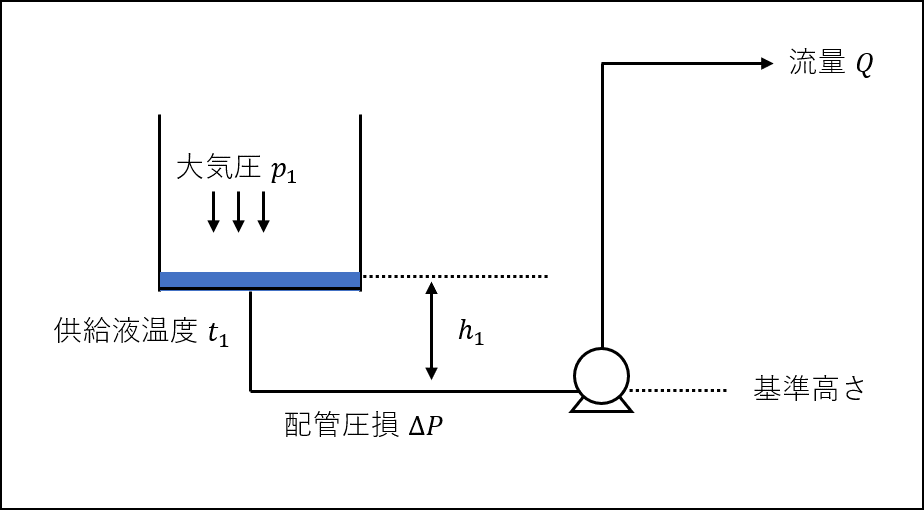
上図のような前提で、NPSHaを数式で表すと下記（２）式のようになります。
ちなみに、NPSHaを言葉で表現すると下記のように表せます。
NPSHa = 圧力ヘッド + 吸込揚程 - 損失ヘッド - 飽和蒸気圧
ここで、上図の吸込揚程\(h_{1}\)は、ポンプの基準高さよりも低いため、負の値をとることに注意してください。
次は、NPSHaの式を導出してみましょう！
流体のエネルギー収支式
次に、NPSHaの導出を行います。
NPSHaを導出するために、流体のエネルギー収支について考えていきます。
流体のエネルギー収支は、下記のような関係になります。
運動エネルギー ＋ 位置エネルギー ＋ 圧力エネルギー = 一定
数式で表してみると、ベルヌイの式と呼ばれる下記（３）式となります。
ベルヌイ（Bernoulli）の式
\(u\) : 流体の速度 [m/s]
\(\rho\): 流体の密度 [kg/m³] ※非圧縮性流体とする（例：水）
\(g\) : 重力加速度 [m/s²]
\(h\) : 高さ [m]
\(p\) : 圧力 [Pa]
ベルヌイの式はぜひ覚えておきましょう！
エネルギー収支式が書けないと計算ミスの要因になります。。
（３）式の各項の単位は、圧力（Pa）となり、圧力収支式の形となっています。
第１項は「動圧」と呼ばれ、第３項は「静圧」と呼ばれます。
また、動圧と静圧を合わせて「全圧」と呼ばれます。
ここで、（３）式の両辺を流体の密度\(\rho\)で割ると、（４）式が得られます。
（４）式の各項の単位は、単位質量あたりのエネルギー（J/kg)となり、エネルギー収支式の形となっています。
同様に、（４）式の両辺をさらに重力加速度\(g\)で割ると、（５）式が得られます。
（５）式の各項の単位は、長さ（m）となり、ヘッドの収支式の形になりました。
（５）式の各項は、下記のように呼ばれます。
$$\textbf{速度ヘッド}\ \ \ \frac {u^{2}}{2g}$$$$\textbf{位置ヘッド}\ \ \ {h}$$$$\textbf{圧力ヘッド}\ \ \ \frac {p}{\rho g}$$
（５）式の第１項速度ヘッドと第３項圧力ヘッドの和は、「全圧ヘッド」になります。
添字１を供給タンク液面、添字２をポンプ吸込口として（５）式を変形すると、ポンプ吸込口（添字２）における全圧ヘッドは下記（６）式のように表せます。
&=\frac {u^{2}_{2}}{2g}+\frac {p_{2}}{\rho g}\\[3pt]
&=\frac {u^{2}_{1}}{2g}+\frac {p_{1}}{\rho g}+\left( h_{1}-h_{2}\right)\end{aligned}\tag{6}$$
供給タンクの速度\(u_{1}\)は無視できるほど小さく、ポンプ吸込口の高さ\(h_{2}\)も、基準高さと同じであるため無視できます。
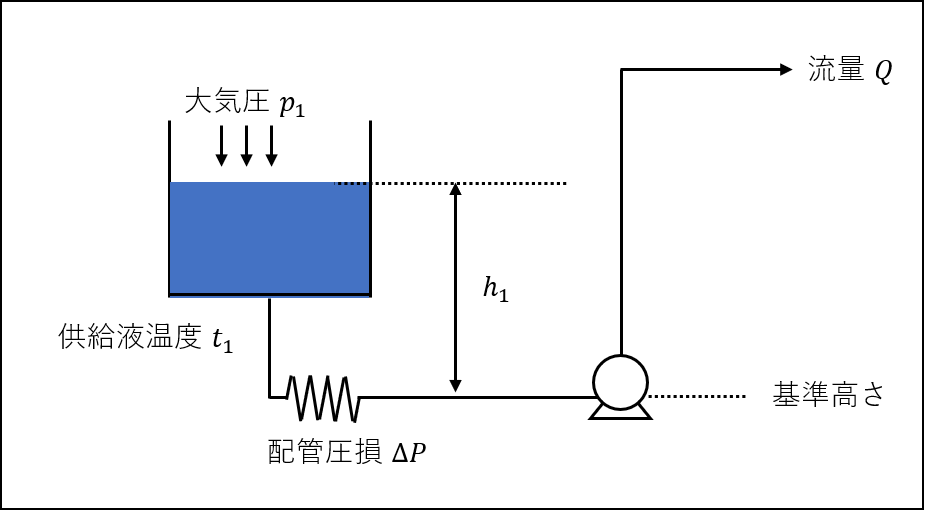
また実際には、配管摩擦による損失ヘッド\(\Sigma F\)を引いてやる必要があるので、（６）式は下記の（７）式になります。
&=\frac {u^{2}_{2}}{2g}+\frac {p_{2}}{\rho g}-\Sigma F\\[3pt]
&=\frac {p_{1}}{\rho g}+h_{1}-\Sigma F\end{aligned}\tag{7}$$
ここで、NPSHaの定義は、ポンプ吸込口の液体が持つ全圧ヘッド（絶対圧基準）から、飽和蒸気圧ヘッドを差し引いたものであるので、NPSHaは下記の（８）式のように表せます。
&=\frac {p_{1}}{\rho g}+h_{1}-\Sigma F-p_{v}\end{aligned}\tag{8}$$
よって、（８）式は（２）式と同じとなり、NPSHaの導出ができました。
次に計算例を紹介します。
NPSHの計算例
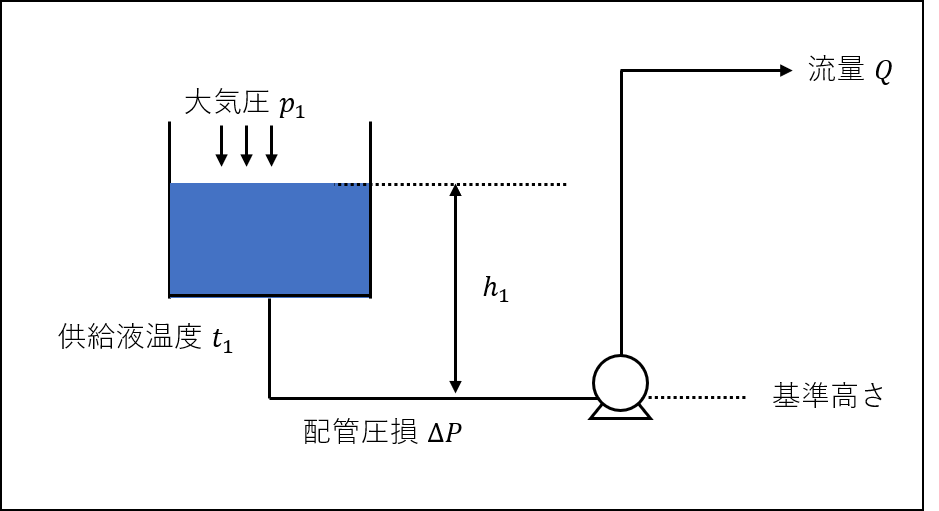
計算例１ 供給タンクが低い位置にある場合
計算前提
供給液の密度 \(\rho = 1,000\) kg/m³
重力加速度 \(g =9.81\) m/s²
供給タンク圧力 \(p_{1} = 101.3\) kPaA（大気圧）
吸込揚程 \(h_{1} = -2.0\) m
吸込配管圧力損失 \(\Delta P = 7.7\) kPa
供給液温度 \(t_{1} = 50\) ℃
飽和蒸気圧 \(P_{v} = 12.3\) kPaA（50℃）
流量 \(Q = 7.0\) m³/min
\(NPSH_{r} = 3.5\) m
それでは早速、上図の前提でNPSHaを計算してみましょう。
（２）式に条件を代入すると、NPSHaは下記のように求まります。
&=\frac {p_{1}}{\rho g}+h_{1}-\frac {\Delta P}{\rho g}-\frac {\ P_{v}}{\rho g}\\[3pt]
&=\frac {101.3\times 1000}{1000\times 9.81}+\left( -2.0\right) -\frac {7.7\times 1000}{1000\times 9.81}-\frac {12.3\times 1000}{1000\times 9.81}\\[5pt]
&=10.3-2.0-0.78-1.26\\[3pt]
&=6.3\ \textrm{m}>3.5\ \textrm{m}\end{aligned}$$
よって上図の例では、\(NPSH_{a} > NPSH_{r}\)となり、ポンプは安全に運転できることがわかりました。
計算例２ 供給タンクが高い位置にある場合
計算前提
供給液の密度 \(\rho = 1,000\) kg/m³
重力加速度 \(g =9.81\) m/s²
供給タンク圧力 \(p_{1} = 101.3\) kPaA（大気圧）
吸込揚程 \(h_{1} = 3.0\) m
吸込配管圧力損失 \(\Delta P = 7.7\) kPa
供給液温度 \(t_{1} = 90\) ℃
飽和蒸気圧 \(P_{v} = 70.1\) kPaA（90℃）
流量 \(Q = 7.0\) m³/min
\(NPSH_{r} = 3.5\) m
次に、供給タンクが高い位置にある場合についてNPSHaを計算してみましょう。
（２）式に条件を代入すると、NPSHaは下記のように求まります。
&=\frac {p_{1}}{\rho g}+h_{1}-\frac {\Delta P}{\rho g}-\frac {\ P_{v}}{\rho g}\\[3pt]
&=\frac {101.3\times 1000}{1000\times 9.81}+\left( 3.0\right) -\frac {7.7\times 1000}{1000\times 9.81}-\frac {70.1\times 1000}{1000\times 9.81}\\[5pt]
&=10.3+3.0-0.78-7.14\\[3pt]
&=5.4\ \textrm{m}>3.5\ \textrm{m}\end{aligned}$$
よって上図の例では、\(NPSH_{a} > NPSH_{r}\)となり、ポンプは安全に運転できることがわかりました。
計算例３ NG例①（温度上昇）
計算前提
供給液の密度 \(\rho = 1,000\) kg/m³
重力加速度 \(g =9.81\) m/s²
供給タンク圧力 \(p_{1} = 101.3\) kPaA（大気圧）
吸込揚程 \(h_{1} = -2.0\) m
吸込配管圧力損失 \(\Delta P = 7.7\) kPa
供給液温度 \(t_{1} = 90\) ℃
飽和蒸気圧 \(P_{v} = 70.1\) kPaA（90℃）
流量 \(Q = 7.0\) m³/min
\(NPSH_{r} = 3.5\) m
次からは、NGとなる例について計算してみましょう。
上図は計算例１とほとんど同じ条件ですが、供給液の温度が上昇しています。
（２）式に条件を代入すると、NPSHaは下記のように求まります。
&=\frac {p_{1}}{\rho g}+h_{1}-\frac {\Delta P}{\rho g}-\frac {\ P_{v}}{\rho g}\\[3pt]
&=\frac {101.3\times 1000}{1000\times 9.81}+\left( -2.0\right) -\frac {7.7\times 1000}{1000\times 9.81}-\frac {70.1\times 1000}{1000\times 9.81}\\[5pt]
&=10.3-2.0-0.78-7.14\\[3pt]
&=0.4\ \textrm{m}<3.5\ \textrm{m}\end{aligned}$$
よって上図の例では、\(NPSH_{a} < NPSH_{r}\)となり、ポンプはキャビテーションを起こす条件であることがわかりました。
計算例４ NG例②（圧力低下）
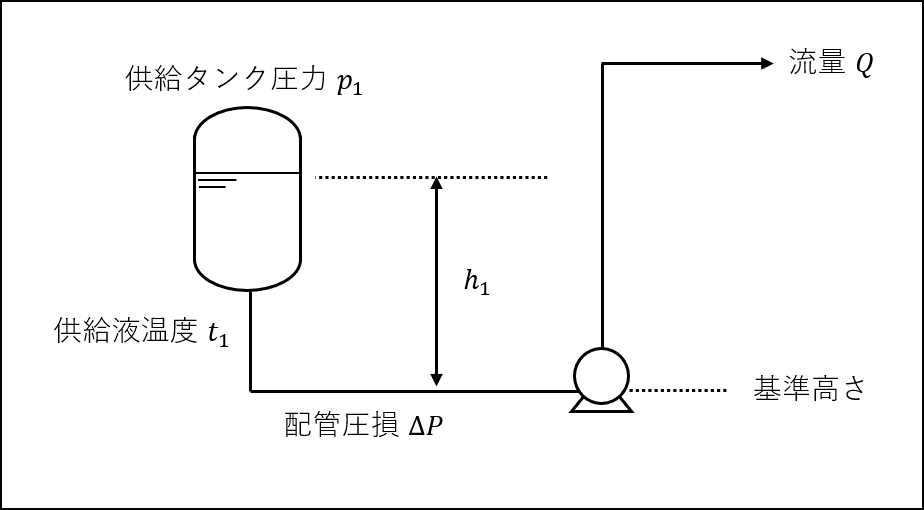
計算前提
供給液の密度 \(\rho = 1,000\) kg/m³
重力加速度 \(g =9.81\) m/s²
供給タンク圧力 \(p_{1} = 50.0\) kPaA（減圧）
吸込揚程 \(h_{1} = 3.0\) m
吸込配管圧力損失 \(\Delta P = 7.7\) kPa
供給液温度 \(t_{1} = 90\) ℃
飽和蒸気圧 \(P_{v} = 70.1\) kPaA（90℃）
流量 \(Q = 7.0\) m³/min
\(NPSH_{r} = 3.5\) m
次は供給タンクの圧力が低下した場合について計算してみましょう。
上図は計算例２とほとんど同じ条件ですが、供給タンクの圧力が低下しています。
（２）式に条件を代入すると、NPSHaは下記のように求まります。
&=\frac {p_{1}}{\rho g}+h_{1}-\frac {\Delta P}{\rho g}-\frac {\ P_{v}}{\rho g}\\[3pt]
&=\frac {50.0\times 1000}{1000\times 9.81}+\left( 3.0\right) -\frac {7.7\times 1000}{1000\times 9.81}-\frac {70.1\times 1000}{1000\times 9.81}\\[5pt]
&=5.1+3.0-0.78-7.14\\[3pt]
&=0.2\ \textrm{m}<3.5\ \textrm{m}\end{aligned}$$
よって上図の例では、\(NPSH_{a} < NPSH_{r}\)となり、ポンプはキャビテーションを起こす条件であることがわかりました。
計算例５ NG例③（液面低下）
計算前提
供給液の密度 \(\rho = 1,000\) kg/m³
重力加速度 \(g =9.81\) m/s²
供給タンク圧力 \(p_{1} = 101.3\) kPaA（減圧）
吸込揚程 \(h_{1} = 1.0\) m
吸込配管圧力損失 \(\Delta P = 7.7\) kPa
供給液温度 \(t_{1} = 90\) ℃
飽和蒸気圧 \(P_{v} = 70.1\) kPaA（90℃）
流量 \(Q = 7.0\) m³/min
\(NPSH_{r} = 3.5\) m
次は供給タンクの液面が低下した場合について計算してみましょう。
上図は計算例２とほとんど同じ条件ですが、供給タンクの液面が低下しています。
（２）式に条件を代入すると、NPSHaは下記のように求まります。
&=\frac {p_{1}}{\rho g}+h_{1}-\frac {\Delta P}{\rho g}-\frac {\ P_{v}}{\rho g}\\[3pt]
&=\frac {101.3\times 1000}{1000\times 9.81}+\left( 1.0\right) -\frac {7.7\times 1000}{1000\times 9.81}-\frac {70.1\times 1000}{1000\times 9.81}\\[5pt]
&=10.3+1.0-0.78-7.14\\[3pt]
&=3.4\ \textrm{m}<3.5\ \textrm{m}\end{aligned}$$
よって上図の例では、\(NPSH_{a} < NPSH_{r}\)となり、ポンプはキャビテーションを起こす条件であることがわかりました。
計算例６ NG例④（圧損増加）
計算前提
供給液の密度 \(\rho = 1,000\) kg/m³
重力加速度 \(g =9.81\) m/s²
供給タンク圧力 \(p_{1} = 101.3\) kPaA（減圧）
吸込揚程 \(h_{1} = 3.0\) m
吸込配管圧力損失 \(\Delta P = 37.7\) kPa
供給液温度 \(t_{1} = 90\) ℃
飽和蒸気圧 \(P_{v} = 70.1\) kPaA（90℃）
流量 \(Q = 7.0\) m³/min
\(NPSH_{r} = 3.5\) m
次は吸込配管の圧力損失が増加した場合について計算してみましょう。
上図は計算例２とほとんど同じ条件ですが、吸込配管の圧力損失が増加しています。
（２）式に条件を代入すると、NPSHaは下記のように求まります。
&=\frac {p_{1}}{\rho g}+h_{1}-\frac {\Delta P}{\rho g}-\frac {\ P_{v}}{\rho g}\\[3pt]
&=\frac {101.3\times 1000}{1000\times 9.81}+\left( 3.0\right) -\frac {37.7\times 1000}{1000\times 9.81}-\frac {70.1\times 1000}{1000\times 9.81}\\[5pt]
&=10.3+3.0-3.84-7.14\\[3pt]
&=2.3\ \textrm{m}<3.5\ \textrm{m}\end{aligned}$$
よって上図の例では、\(NPSH_{a} < NPSH_{r}\)となり、ポンプはキャビテーションを起こす条件であることがわかりました。
キャビテーション対策
現場で遭遇しうる問題について、表でまとめてみました。
| キャビテーション（NPSHaが不足）原因 | 対策 |
| 供給タンクの圧力低下 | タンクを加圧する |
| 供給タンク液面が低い | 管理液面を上げる タンクの位置を上げる ポンプの位置を下げる |
| 吸込側配管の圧力損失が大きい | バルブを撤去する バルブを低圧損タイプに変更する （例：グローブ弁→ボール弁） 配管内のスケールや錆、藻などの異物を取り除く |
| 液の温度が高い | 冷却する |
ちなみに、NPSHrを改善するためには、ポンプの効率を犠牲にする必要があります。
（１）式からわかるように、NPSHrを小さくするためには、吸込比速度を大きくしないといけません。
しかし、吸込比速度を大きく設計すると、ポンプの効率が低下してしまいます。
一般に、吸込比速度は1200→1800（1.5倍）が上限であり、ポンプの効率を犠牲にしてもNPSHrは４割減が限界だと言われています。
まとめ
ポイント
- NPSHは、ポンプがキャビテーションを起こすことなく、安全に運転できる範囲を示す指標
- NPSHrは、ポンプ固有のヘッドで、ポンプが液を吸い込むために必要な全圧ヘッド（速度ヘッド＋圧力ヘッド）である
- $$NPSH_{r}\left( NPSH3\right) =\left( \frac {N\sqrt {Q}}{S}\right) ^{\frac {4}{3}}$$
- NPSHaは、ポンプ吸込口の液体がもつ全圧ヘッドから飽和蒸気圧ヘッドを引いたもの
- $$NPSH_{a}=\frac {p_{1}}{\rho g}+h_{1}-\Sigma F-p_{v}$$
- \(NPSH_{a} >NPSH_{r}\)となれば、ポンプは安全に運転が可能。
- \(NPSH_{a} <NPSH_{r}\)となる場合、ポンプはキャビテーションを起こす。
