どうも。こんにちは。
ケミカルエンジニアのこーしです。
本日は、コントロールバルブ(CV、調節弁)の圧力損失の計算方法について、わかりやすく解説していきます。
この記事を読むことで、既設コントロールバルブの圧力損失や新設バルブの設計に必要なCv値が算出できるようになります。
本記事の内容
・コントロールバルブとは
・Cv値とは
・Cv値の計算式(SI単位系)
・コントロールバルブの固有流量特性
・既設コントロールバルブの計算例
・コントロールバルブの設計例
この記事を書いた人
 こーし(@mimikousi)
こーし(@mimikousi)
目次
コントロールバルブとは
コントロールバルブ(CV、調節弁)とは、ガス、蒸気、水、または化学化合物などの流体を操作して、流量・圧力・温度・液面などのプロセス変数を希望の設定値に制御するバルブのことです。
コントロールバルブは、調節部からの信号を受け、バルブの作動に必要な動力を補助動力源(電気、圧縮空気など)から受けます。
コントロールバルブの仕組みについて詳しく知りたい場合は、下記のサイトを参考にしてください。
非常にわかりやすく記載してありますので、オススメです。
Cv値とは
同じ種類、同じ口径のバルブでも、全開にしたときの流量は、バルブメーカーによって様々であるため、統一した基準を設けています。
それが容量係数と呼ばれるもので、Cv値、Kv値、Av値などがあります。
一般的に使用されるのがCv値であるため、今回はCv値について解説していきます。
【Cv値とは】
弁の入口と出口の差圧を1Psi(=lbf/in²)として、60°F(= 15℃)の清水を流したときの流量をUS gal/minで表した数値
よって、Cv値は下記(1)式で求めることができます。
また、(1)式を流量計算式に変換したものを(2)式に示します。
$$C_{v}=Q\times \sqrt {\frac {G}{\Delta p}}\ \tag{1}$$
$$Q=C_{v}\times \sqrt {\frac {\Delta p}{G}}\ \tag{2}$$
\(C_{v}\):\(C_{v}\)値
\(Q\):流量 [US gal/min]
\(G\):比重 [-]
\(\Delta p\):差圧 [psi=lbf/in²]
(2)式からわかるように、Cv値が大きいほど、流量Qは大きくなり、またCv値が一定のときは、差圧Δpが大きいほど、流量が増加します。
例えば、あるコントロールバルブの差圧が1Psi(=lbf/in²)で、60°F(= 15℃)の清水が100 US gal/min流れる場合、Cv値は100となります。
ポイント
・1 US gal(米ガロン)= 3.785412 L
・1 lbf(重量ポンド) = 4.448221 N
・1 in(インチ) = 0.0254 m
次は、SI単位系に変換したCv値の計算式を紹介します!
Cv値の計算式(SI単位系)
液体、気体、水蒸気のCv値の計算式を説明していきます。
メーカーによって、Cv値の計算式が若干異なるのは、使用する単位系が異なるからです。
本質はどれも同じなので、気にしないで計算していきましょう。
1.液体
(1)式をSI単位系に変換すると、下記(3)式で表すことができます。
また、(3)式を流量計算式に変換したものを(4)式に示しました。
$$C_{v}=0.366Q_{L}\sqrt {\frac {G_{L}}{\Delta p}}\ \tag{3}$$
$$Q_{L}=\frac {C_{v}}{0.366\sqrt {\frac {G_{L}}{\Delta p}}}\ \tag{4}$$
\(Q_{L}\):液体の流量 [m³/h]
\(G_{L}\):液体の比重 [-]
\(\Delta p\):差圧 [MPa]
(3)、(4)式は、レイノルズ数が大きく、乱流の場合で成り立ちますが、層流の場合は粘度補正が必要になります。
実際に取り扱う流体は、ほとんどの場合が乱流なので問題ありませんが、もし層流だった場合は、下記リンクを参考にしてください。
2.気体(ガス)
気体の場合、差圧\(\Delta p\)が弁入口圧力の半分(\(\frac {P_{1}}{2}\))よりも大きくなると、それ以上差圧\(\Delta p\)を大きくしても流量が増加しない領域となります。
よって、Cv値の計算式は、差圧\(\Delta p\)の大きさで場合分けして下記のように表します。
① \(\Delta p <\frac {P_{1}}{2}\)の場合(差圧が小さい場合)
\(Q_{G}\):気体の流量 [m³/h]
\(G_{G}\):気体の比重 [-]
\(P_{1}\) :弁入口圧力(一次圧) [MPaA]
\(P_{2}\) :弁出口圧力(二次圧) [MPaA]
\(\Delta p\):差圧 [MPa]
\(t\) :気体の温度 [℃]
② \(\Delta p\geq \frac {P_{1}}{2}\)の場合(差圧が大きい場合)
$$C_{v}=\frac {Q_{G}\sqrt {G_{G}\left( 273+t\right) }}{2519P_{1}}\ \tag{7}$$
$$Q_{G}=\frac {2519C_{v}P_{1}}{\sqrt {G_{G}\left( 273+t\right) }}\ \tag{8}$$
\(Q_{G}\):気体の流量 [m³/h]
\(G_{G}\):気体の比重 [-]
\(P_{1}\) :弁入口圧力(一次圧) [MPaA]
\(t\) :気体の温度 [℃]
3.水蒸気
気体と同様、水蒸気のCv値の計算式は、差圧\(\Delta p\)の大きさで場合分けして下記のように表します。
① \(\Delta p <\frac {P_{1}}{2}\)の場合(差圧が小さい場合)
\(Q_{s}\):水蒸気の流量 [kg/h]
\(P_{1}\) :弁入口圧力(一次圧) [MPaA]
\(P_{2}\) :弁出口圧力(二次圧) [MPaA]
\(\Delta p\):差圧 [MPa]
\(S\) :水蒸気の過熱度 [℃] (過熱蒸気温度ー飽和蒸気温度)
※飽和蒸気のときは、\(S=0\)
② \(\Delta p\geq \frac {P_{1}}{2}\)の場合(差圧が大きい場合)
\(Q_{s}\):水蒸気の流量 [kg/h]
\(P_{1}\) :弁入口圧力(一次圧) [MPaA]
\(S\) :水蒸気の過熱度 [℃] (過熱蒸気温度ー飽和蒸気温度)
※飽和蒸気のときは、\(S=0\)
コントロールバルブの固有流量特性
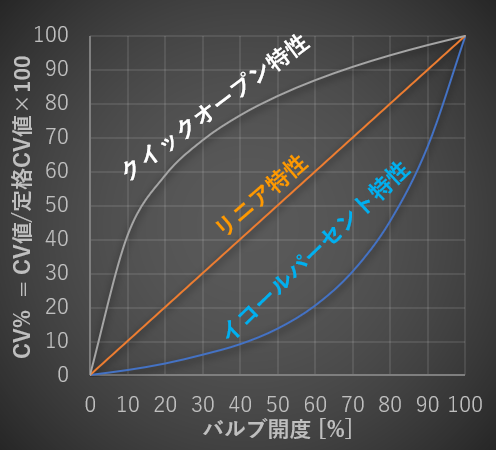
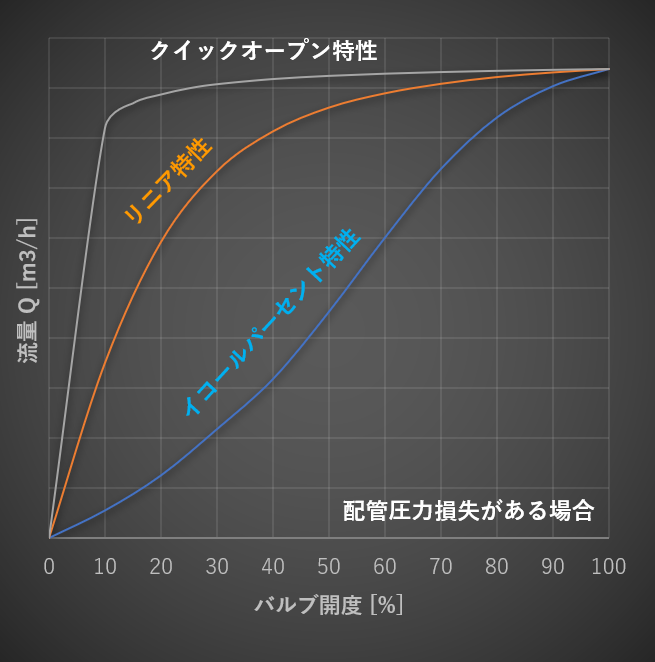
コントロールバルブの開度(0~100%)とCv値の関係を、コントロールバルブの固有流量特性といい、代表的な3種類を下記に示します。
-
リニア特性
-
イコールパーセント特性
-
クイックオープン特性
それでは、それぞれの流量特性の特徴について説明していきます。
1.リニア特性
バルブ開度 [%]とCv値 が比例関係になります。
バルブの差圧変動が少ない系において、よく使われます。
バルブの差圧\(\Delta p\)が一定の場合、バルブ開度と流量の関係についても、下図のように比例関係となります。
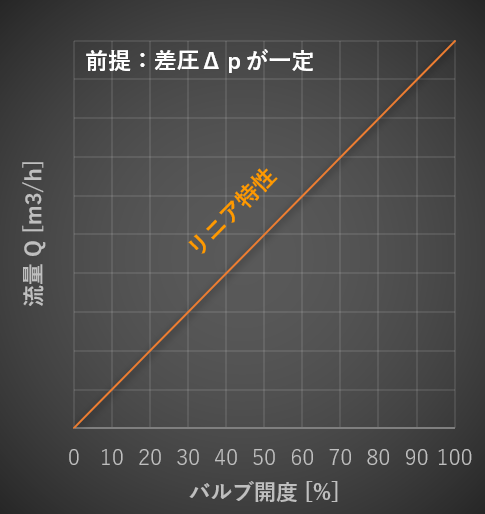
リニア特性は、バルブ開度とCv値が比例関係なので、差圧\(\Delta p\)が一定の場合、バルブ開度と流量も比例関係となります。
2.イコールパーセント特性
ケミカルプラントで最もよく使われているバルブの流量特性です。
イコールパーセント特性では、バルブ開度が大きくなるとCv値が指数関数的に増加します。
しかし、配管圧力損失を考慮すると、バルブ開度と流量の関係は、比例関係に近づきます。
なぜなら、配管圧力損失は流量の2乗に比例して大きくなるため、バルブの差圧\(\Delta p\)が小さくなるからです。
$$Q=C_{v}\times \sqrt {\frac {\Delta p}{G}}\ \tag{2}$$
(2)式からわかるように、バルブの差圧\(\Delta p\)が小さくなると流量は低下します。
Cv値が指数関数的に増加しても、バルブの差圧が小さくなっていくため、バルブ開度と流量の関係は、比例関係に近づきます。
非常に大事な概念ですので、図示してみます。
【配管圧力損失によるバルブ差圧\(\Delta p\)の低下】
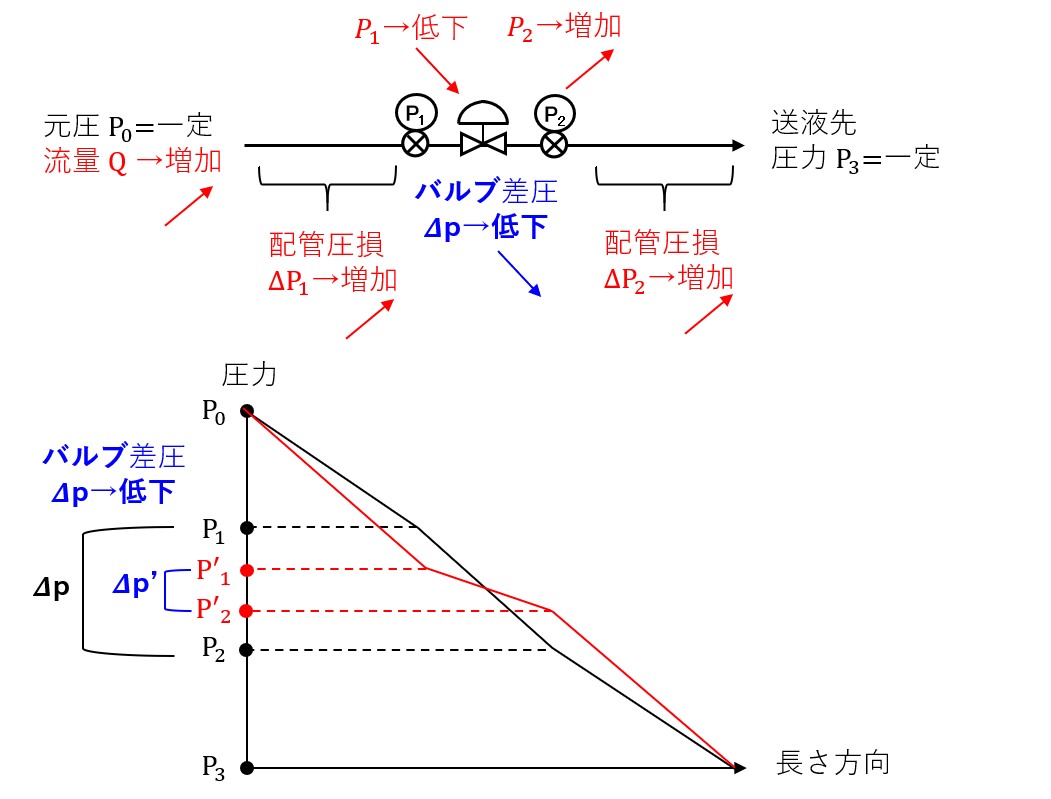
流量\(Q\)が増加すると、配管圧力損失が増加するため、バルブの1次圧(P1)は低下し、バルブの2次圧(P2)は上昇します。
よって、バルブの差圧\(\Delta p\)は低下します。
【バルブ開度と流量\(Q\)の関係】
配管圧力損失がある場合、すなわち、バルブの差圧\(\Delta p\)が変化する場合、イコールパーセント特性では、バルブ開度と流量の関係が比例関係に近づきます。(下図参照)
一方、リニア特性のバルブ開度と流量の関係は、比例でなくなることがわかります。
よって、ケミカルプラントで「イコールパーセント特性」がよく使われている理由がよくわかったと思います。
配管の圧力損失計算については、下記リンクで詳しく解説してます。
-

-
【解説】配管圧力損失の計算方法
続きを見る
3.クイックオープン特性(ON-OFF弁)
クイックオープン特性は、上図のバルブ開度と流量の関係からわかるように、バルブ開度を少し開けただけで、最大流量近くまで一気に増加します。
バルブ開度がある程度開いてくると、それ以上開いても流量が全然増加しなくなります。
このような特性から、ON-OFF弁とも呼ばれています。
4.流量特性の選定方法
バルブ選定時は、流量変化がなるべくバルブ開度変化に比例するように流量特性を選定します。
- リニア特性 → バルブの差圧変動が少ない系(配管圧力損失が無視できる系)で使用
- イコールパーセント特性 → 配管の圧力損失が無視できない系で使用
- クイックオープン特性 → ON-OFF弁として使いたい場合に使用
既設コントロールバルブの計算例
計算例① コントロールバルブの圧力損失計算
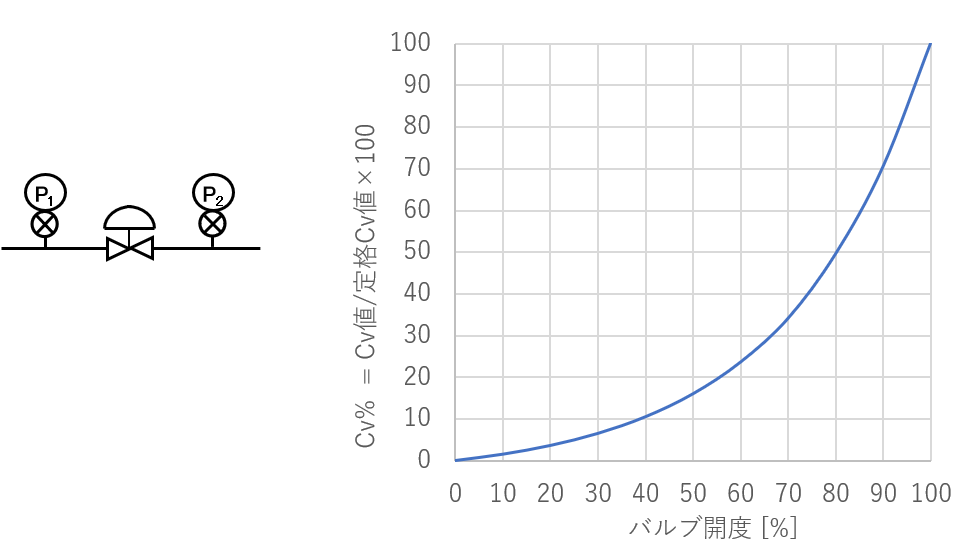
計算前提
定格Cv値 \(C_{v} = 100\)
水蒸気の流量 \(Q_{s} = 450\) kg/h
弁入口圧力(一次圧) \(P_{1} = 0.60\) MPaG ※ゲージ圧
水蒸気の過熱度\(S = 10\) ℃
バルブ開度 40%
\(\Delta p <\frac {P_{1}}{2}\)と仮定し、(9)式を変形してコントロールバルブの圧力損失\(\Delta p\)を計算していきます。
まず、(9)式の両辺を2乗して整理してみます。
&=\frac {Q^{2}_{s}}{138.7^{2}\left( P_{1}-P_{2}\right) \left( P_{1}+P_{2}\right) }\left( 1+0.0013S\right) ^{2}\\[5pt]
&=\frac {Q^{2}_{s}}{138.7^{2}\left( P^{2}_{1}-P^{2}_{2}\right) }\left( 1+0.0013S\right) ^{2}\\[5pt]
P^{2}_{1}-P^{2}_{2}&=\frac {Q^{2}_{s}\left( 1+0.0013S\right) ^{2}}{138.7^{2}C^{2}_{v}}\\[5pt]
P^{2}_{2}&=P^{2}_{1}-\frac {Q^{2}_{s}\left( 1+0.0013S\right) ^{2}}{138.7^{2}C^{2}_{v}}\end{aligned}$$
よって、
また、計算前提のグラフより、バルブ開度40%のときのCv%は10%と読み取ることができます。
よって、Cv値は定格Cv値にCv%を掛けて求めることができます。
$$C_{v}=100\times \frac {10}{100}=10$$
Cv値が求まりましたので、(13)式を用いてコントロールバルブの圧力損失が計算できます。
&=\sqrt {\left( 0.60+0.1013\right) ^{2}-\frac {450^{2}\left( 1+0.0013\times 10\right) ^{2}}{138.7^{2}\times 10^{2}}}\\[5pt]
&=0.6195\ \textrm{MPaA}\end{aligned}$$
よって、
$$\Delta p=\left( 0.60+0.1013\right) - 0.6195=0.082\ \textrm{MPa}$$
ここで、\(\Delta p <\frac {P_{1}}{2}\)という仮定が正しいことを確認しておきます。
以上より、バルブ開度と流量\(Q\)が既知の場合、Cv値の計算式からコントロールバルブの圧力損失\(\Delta p\)を算出することができました。
計算例② コンプレッサー必要吐出圧力
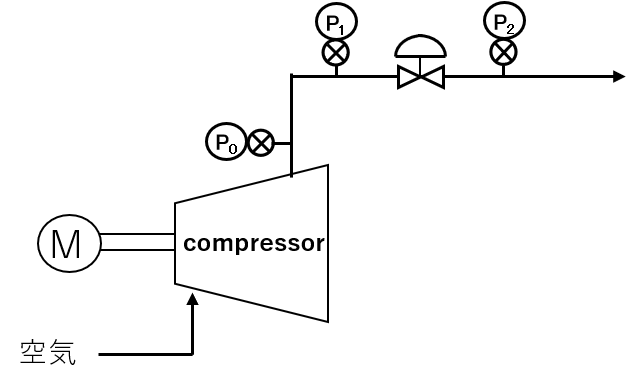
計算前提
定格Cv値 \(C_{v} = 30\)
圧縮空気流量 \(Q_{G} = 4500\) Nm3/h ※標準状態(大気圧、0℃)における流量
弁出口圧力(二次圧) \(P_{2} = 5.50\) MPaG ※ゲージ圧
圧縮空気温度 \(t = 50\) ℃
比重 \(G_{G} =1 \)
(1)バルブ開度80%のとき
\(\Delta p <\frac {P_{1}}{2}\)と仮定し、(6)式を変形して弁入口圧力\(P_{1}\)を計算していきます。
$$Q_{G}=2916C_{v}\sqrt {\frac {\Delta p\left( P_{1}+P_{2}\right) }{G_{G}\left( 273+t\right) }}\ \tag{6}$$
まず、(6)式の両辺を2乗して整理してみます。
$$\begin{aligned}Q^{2}_{G}&=2916^{2}C^{2}_{v}\frac {\left( P_{1}-P_{2}\right) \left( P_{1}+P_{2}\right) }{G_{G}\left( 273+t\right) }\\[5pt]
&=2916^{2}C^{2}_{v}\frac {P^{2}_{1}-P^{2}_{2}}{G_{G}\left( 273+t\right) }\\[5pt]
P^{2}_{1}-P^{2}_{2}&=\frac {Q^{2}_{G}G_{G}\left( 273+t\right) }{2916^{2}C^{2}_{v}}\\[5pt]
P^{2}_{1}&=P^{2}_{2}+\frac {Q^{2}_{G}G_{G}\left( 273+t\right) }{2916^{2}C^{2}_{v}}\end{aligned}$$
よって、
$$P_{1}=\sqrt {P^{2}_{2}+\frac {Q^{2}_{G}G_{G}\left( 273+t\right) }{2916^{2}C^{2}_{v}}}\ \tag{14}$$
ここで、計算例①で使用したバルブ開度とCv%のグラフより、バルブ開度80%のときのCv%を読み取ります。
よって、Cv値は下記のように求まります。
$$C_{v}=30\times \frac {50}{100}=15$$
先ほど求めた(14)式にCv値を代入すると、弁入口圧力\(P_{1}\)は下記のように求まります。
&=5.90\ \textrm{MPaA}\\[5pt]
&=5.80\ \textrm{MPaG}\end{aligned}$$
よって、
$$\Delta p=5.80 - 5.50=0.30\ \textrm{MPa}$$
となり、\(\Delta p <\frac {P_{1}}{2}\)という仮定が正しいことがわかりました。
(2)バルブ開度90%のとき
次は、バルブ開度を少しだけ開いた場合のコンプレッサーの必要吐出圧力を算出します。
(1)と同様に、計算例①で使用したバルブ開度とCv%のグラフより、バルブ開度90%のときのCv%を読み取ります。
よって、Cv値は下記のように求まります。
$$C_{v}=30\times \frac {70}{100}=21$$
(1)と同様に、\(\Delta p <\frac {P_{1}}{2}\)と仮定し、(14)式にCv値を代入して、弁入口圧力\(P_{1}\)を求めます。
&=5.75\ \textrm{MPaA}\\[5pt]
&=5.65\ \textrm{MPaG}\end{aligned}$$
$$\Delta p=5.65 - 5.50=0.15\ \textrm{MPa}$$
よって、\(\Delta p <\frac {P_{1}}{2}\)という仮定が正しいことがわかりました。
以上より、流量一定の条件でバルブ開度を開くと、コンプレッサーの必要吐出圧力が低下するということがわかりました。
できるだけバルブ開度の大きいところで運転し、コンプレッサーの吐出圧力を下げて省エネ運転したいですね。
コントロールバルブの設計例
計算例③ 流量コントロールバルブのCv値
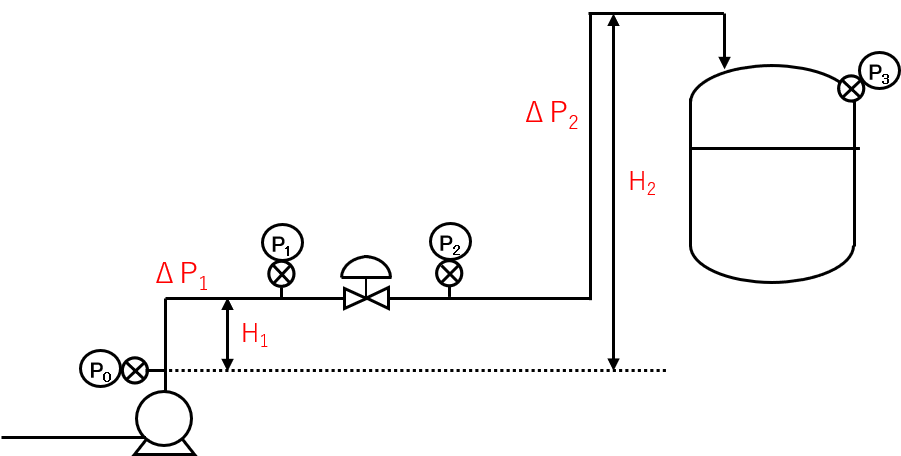
計算前提
目標バルブ開度 40% (計算例①のグラフより、Cv%=10%)
液体流量 \(Q_{L} = 30\) m3/h
液体の比重 \(G_{L} =1 \)
ポンプ吐出圧力 \(P_{0} = 0.40\) MPaG
送液タンク圧力 \(P_{3} = 0.20\) MPaG
バルブ一次側の配管圧力損失 \(\Delta P_{1} =0.005\) MPa
バルブ二次側の配管圧力損失 \(\Delta P_{2} =0.02\) MPa
バルブ一次側のヘッド増加分 \(\rho gH_{1} = 0.005\) MPa
バルブ二次側のヘッド増加分 \(\rho g\left(H_{2}-H_{1}\right)= 0.03\) MPa
液体の密度 \(\rho\) [kg/m³]
重力加速度 \(g\) [m/s²]
液体のCv値計算ですので、(3)式を用います。
$$C_{v}=0.366Q_{L}\sqrt {\frac {G_{L}}{\Delta p}}\ \tag{3}$$
まず、バルブの差圧\(\Delta p\)を求めます。
計算前提から下記のように求めることができます。
バルブの一次圧は、ポンプの吐出圧から配管圧力損失と辺土の増加分を引いて求めます。
$$\begin{aligned}P_{1}&=P_{0}-\Delta P_{1}-\rho gH\\[3pt]
&=0.40-0.005-0.005\\[3pt]
&=0.39\ \textrm{MPaG}\end{aligned}$$
一方、バルブの二次圧は、送液タンクの圧力から配管圧力損失とヘッドの増加分を足して求めます。
$$\begin{aligned}P_{2}&=P_{3}+\Delta P_{2}+\rho g\left(H_{2}-H_{1}\right)\\[3pt]
&=0.20+0.02+0.03\\[3pt]
&=0.25\ \textrm{MPaG}\end{aligned}$$
よって、バルブの差圧\(\Delta p\)は下記のように求まります。
$$\begin{aligned}\Delta p &= P_{1}-P_{2}\\[3pt]
&=0.39-0.25\\[3pt]
&=0.14\ \textrm{MPa}\end{aligned}$$
よって、(3)式に\(\Delta p\)を代入すると、
$$\begin{aligned}C_{v}&=0.366\times 30\times \sqrt {\frac {1}{0.14}}\\[3pt]
&=29.3\end{aligned}$$
したがって、バルブ開度40%のとき、Cv%は10%ですので、定格Cv値は下記のように求まります。
$$\begin{aligned}\textrm{定格}C_{v}&=\frac {Cv}{\left( \frac {10}{100}\right) }\\[3pt]
&=29.3\times 10\\[3pt]
&=293\end{aligned}$$
以上のように、定格Cv値を算出し、バルブを設計します。
ヘッド増加分\(\rho gH\)が理解できないと思ったら下記リンクを参考にしてください。
-

-
【わかりやすく解説】ポンプの全揚程の計算方法
続きを見る
まとめ
ポイント
- Cv値は容量係数と呼ばれるもので、バルブを通過する流体の流量を表す統一基準のこと。
- Cv値の計算式は、メーカーによってバラバラであるが、それは使用する単位の違いが原因である。
- コントロールバルブの固有流量特性には、①リニア特性、②イコールパーセント特性、③クイックオープン特性がある。
- ケミカルプラントでは、イコールパーセント特性が使われることが多い。
- バルブの流量特性は、バルブ開度と流量が比例関係になるものを選定する。
- 配管圧力損失が無視できない場合、バルブ開度と流量が比例関係になるのは、イコールパーセント特性である。


