また、t検定の手順や結果の書き方が知りたいな。
こんなお悩みを解決します。
どうも。こんにちは。ケミカルエンジニアのこーしです。
本日は、「現場で使えるt検定」について、わかりやすく解説します。
本記事では例題を用いて解説しますので、どのような場合にt検定を実施し、どのように検定結果を報告すべきかわかるようになります。
t検定には下記2通りの方法があり、今回は【パターン①】t分布表を用いたt検定を解説します。

【パターン②】p値を用いたt検定については、下記の記事で解説しています。
-

-
現場で使えるエクセルによるt検定(p値を用いた検定)
続きを見る
本記事の内容
- t検定とは
- t検定の手順(結果の書き方)
- t検定の種類(場合分け)
- t検定の例題
①母平均の検定
②平均値の差の検定(独立な2群)
③平均値の差の検定(対応のある2群)
④母分散の差の検定
⑤無相関検定 - 参考文献
この記事を書いた人
 こーし(@mimikousi)
こーし(@mimikousi)
目次
t検定とは
t検定とは、簡単に言えば「平均値の差の有無」や「相関関係の有無」を統計的に判断する方法のことです。
ちなみに、t検定の定義は下記のとおりです。
帰無仮説が正しいと仮定した際に、検定統計量tがt分布に従うことを利用した検定
帰無仮説や検定統計量、t分布など、よくわからない用語が出てきました。
最初から理解する必要はないので、定義は読み飛ばしてもらって構いません。
本記事を読み進めていただければ、理解できるハズです!
t分布とは
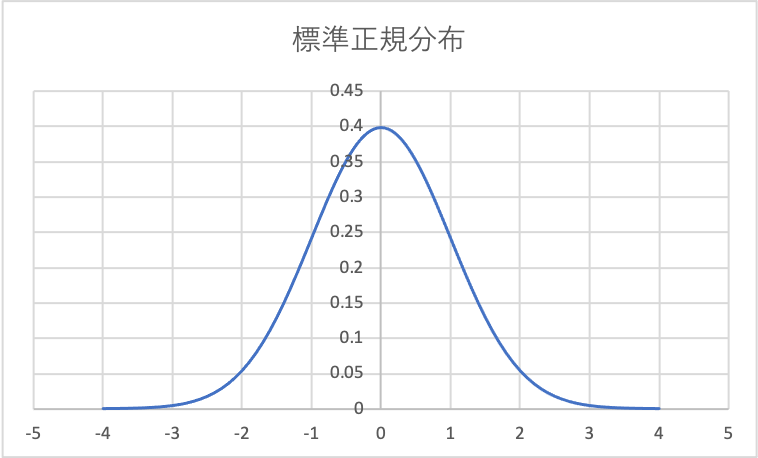
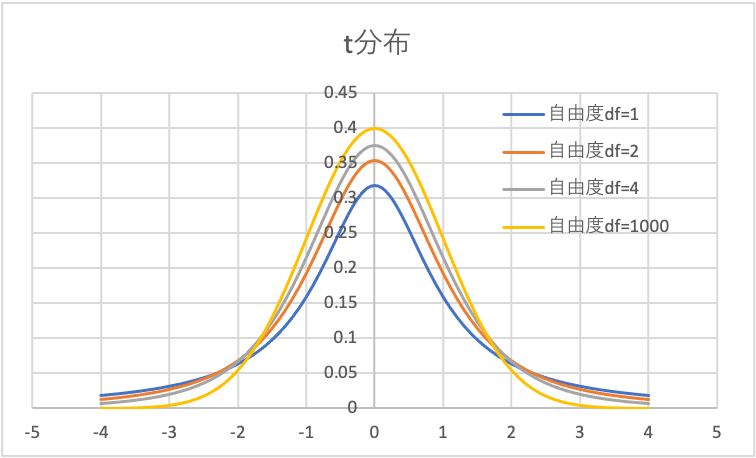
上図に、正規分布とt分布を比較してみました。
正規分布は、統計的手法の基本となる分布です。
正規分布がよくわからない方は、コチラを参照してください。
一方、t分布は、自由度によって分布の形が変わるのが特徴です。
自由度の概念は難しいですが、「自由な値を取り得る”データの数”」と考えてもらえば問題ないです。
自由度が無限大に大きくなると、t分布は正規分布に一致します。
目安として、データ数が100以上(できれば400以上)ある場合、検定統計量tは正規分布に従うと見なして検定を行うことができます。
ただし、検定統計量が正規分布に従う場合は、t検定ではなく「z検定」と呼ばれます。
よって、t検定はデータ数が少ない場合に使われる検定方法と考えてもよいです。
帰無仮説と対立仮説
帰無仮説とは、「無に帰するべき仮説」のことで、一般に「捨てたい仮説」を帰無仮説に設定します。
仮説検定(t検定やz検定など)を行って、仮説が間違っていたときは、帰無仮説を「棄却する」と言います。
一方、仮説を捨てずに採用することを「採択する」といいます。
ちなみに、帰無仮説が棄却された場合に採用されるのが、「対立仮説」です。
【例】 相関があるかどうかを調べたい場合
「相関がある」ことを証明したい場合は、帰無仮説を「相関が無い(相関係数がゼロ)」としましょう。
なぜなら、「相関がある」を帰無仮説にしてしまうと、下記のように程度の異なる「相関がある」を定義できてしまうため、帰無仮説を棄却することが難しくなるからです。
- 強い相関がある
- 中程度の相関がある
- 弱い相関がある
また、帰無仮説を「棄却する」ときは、対立仮説を採択する強い主張となりますが、帰無仮説を「棄却できない」ときは、「帰無仮説が正しい」という意味にはなりません。
帰無仮説を単に「棄却できない」だけであり、「判断を留保する」という意味なので注意しましょう!
例えば、「平均値の差の有無」を検定をしたい場合は、「平均値の差が無い」を帰無仮説に設定します。
そして、帰無仮説が棄却できるときは「平均値に差がある」と言えますが、帰無仮説が棄却できなかった場合は「平均値に差があるとは言えない」という結論になります(差が無いとは言い切れないということです)。
有意水準とは
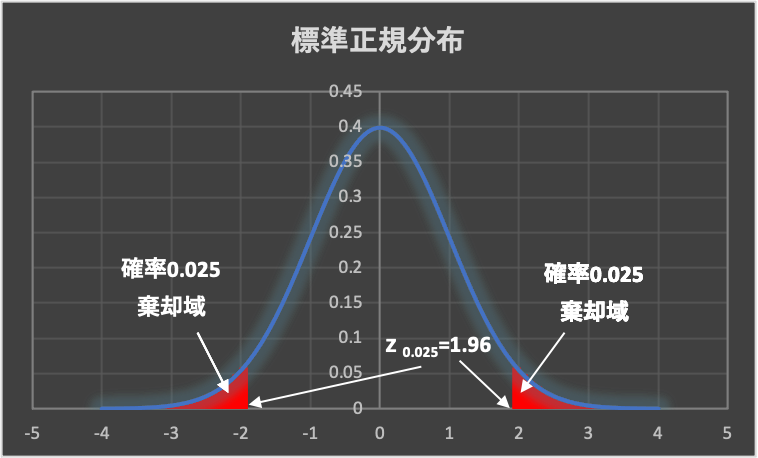
帰無仮説が正しいと仮定した際に、「”まれ”にしか生じ得ない事象」が起こる確率を「有意水準(α)」と呼びます。
上図の赤の部分が、有意水準5%(片側2.5%ずつの両側で5%)の範囲を表しており、「棄却域」と呼ばれます。
データから算出した検定統計量(t値など)が「棄却域」に入っていると、有意である(有意差あり)と見なされます。
ちなみに、慣例として有意水準は”5%”がよく使われます。
帰無仮説が正しかった場合でも、5%は棄却される可能性があるということです(第1種の誤り)
5%は大きいと思うかもしれませんが、これを1%や0.1%に設定すると、今度は帰無仮説が間違っていても、帰無仮説が採択される可能性が高まってしまいます(第2種の誤り)。
つまり、数字を大きくしても小さくしてもトレードオフの関係にあるため、絶妙なバランス感覚が必要であり慣例的に5%に落ち着いたようです。(詳しい解説はこちら)
1%や10%にする場合もありますが、使う際は何かしら理由が必要です。(勝手にやると結論を操作しているように思われてしまいます)
両側検定と片側検定
分布の両側に棄却域を設定する検定方式を「両側検定」と言います。
例えば、製品の直径が規格より大きくても小さくても良くない場合は、「両側検定」を用い、大きいのは困るが小さい分には構わない場合は、棄却域が片側だけにある「片側検定」を用います。
t検定の手順(結果の書き方)
それでは、t検定の手順を見ていきましょう。
t検定の結果の書き方もこの手順に従って書きます。
- 仮説の設定
帰無仮説\(H_0\)と対立仮説\(H_1\)を設定 - 検定統計量(z,t, Fなど)の算出
- 棄却域の設定
まず有意水準\(\alpha\)(基本5%)を決め、棄却域を求める - 判定
正規分布表もしくは、t分布表を読み取り、データから算出した検定統計量が、
・棄却域に入る → 帰無仮説を棄却
・棄却域に入らない → 帰無仮説を採択 - 結論
t検定の種類(場合分け)
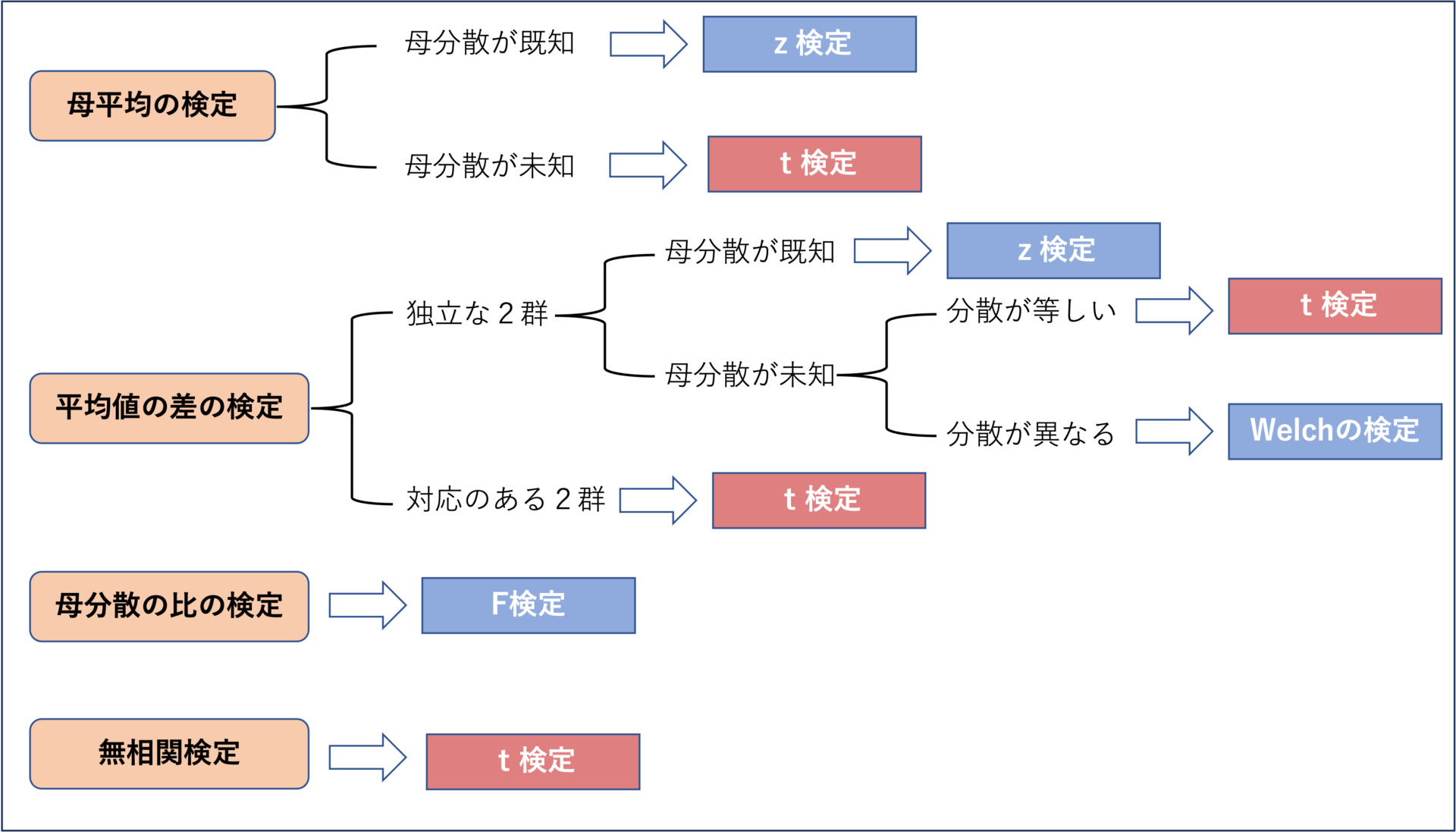
上図に、t検定の種類と場合分けを示しました。
「何を検定したいのか」によって、使うべき検定統計量(z、t、Fなど)が異なります。
使うべき検定統計量の選び方については、例題を使って順番に解説していきます。
注意ポイント
本記事では、母集団は正規分布に従うことを前提にしています。
サンプル数が少なく(中心極限定理が使えない)、正規分布でない場合については、本記事の範囲外とします。
t検定の例題
母平均の検定(母分散が既知の場合)
生産設備(量産機)の品質データなど正規分布に従う母集団では、サンプル(検定したいデータ)の平均が母平均と同じかどうかを検定により判断することができます。
【例題①】品質変化の有無
製品\(A\)の品質(不純物濃度)が変化していないかどうかを検定してみます。
製品\(A\)の不純物濃度の平均値(母平均)が\(\mu_0 = 300\)ppm、母分散が\(\sigma^2 = 8^2\)であったとき、直近生産した製品\(A\)(サンプル)の不純物濃度の平均値が\(\bar{x} = 303\)ppm(n=100)でした。
※標本(サンプル)の分散は母分散と等しいとします(つまり母分散が既知の場合)
それでは、検定の手順に従い、例題を解いていきましょう。
例題①は、母分散が既知の場合の母平均の検定ですので、「z検定」です。
よって、検定統計量zが正規分布に従います。(標準正規分布表を参照します)
1.仮説の設定
帰無仮説\(H_0 \):\(\mu = 300\) ppm(サンプルの母平均も300ppm)
対立仮説\(H_1 \):\(\mu \neq 300\) ppm(サンプルの母平均は300ppmではない)
大きくても小さくても差があれば、「変化あり」ですので「両側検定」です。
2.検定統計量の算出
母分散が既知であるため、検定統計量zを使用します。
$$\begin{aligned}z&=\frac{\bar{x}-\mu _{0}}{\frac{\sigma }{\sqrt{n}}}\\[5pt]
&=\frac{303-300}{\frac{8}{\sqrt{100}}}\\[5pt]
&=3.75\end{aligned}$$
3.棄却域の設定
有意水準は、\(\alpha = 0.05\left( 5\% \right)\)とします。
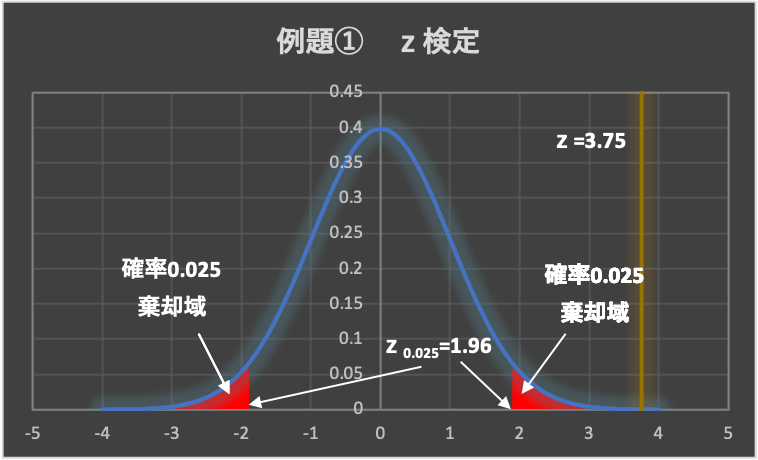
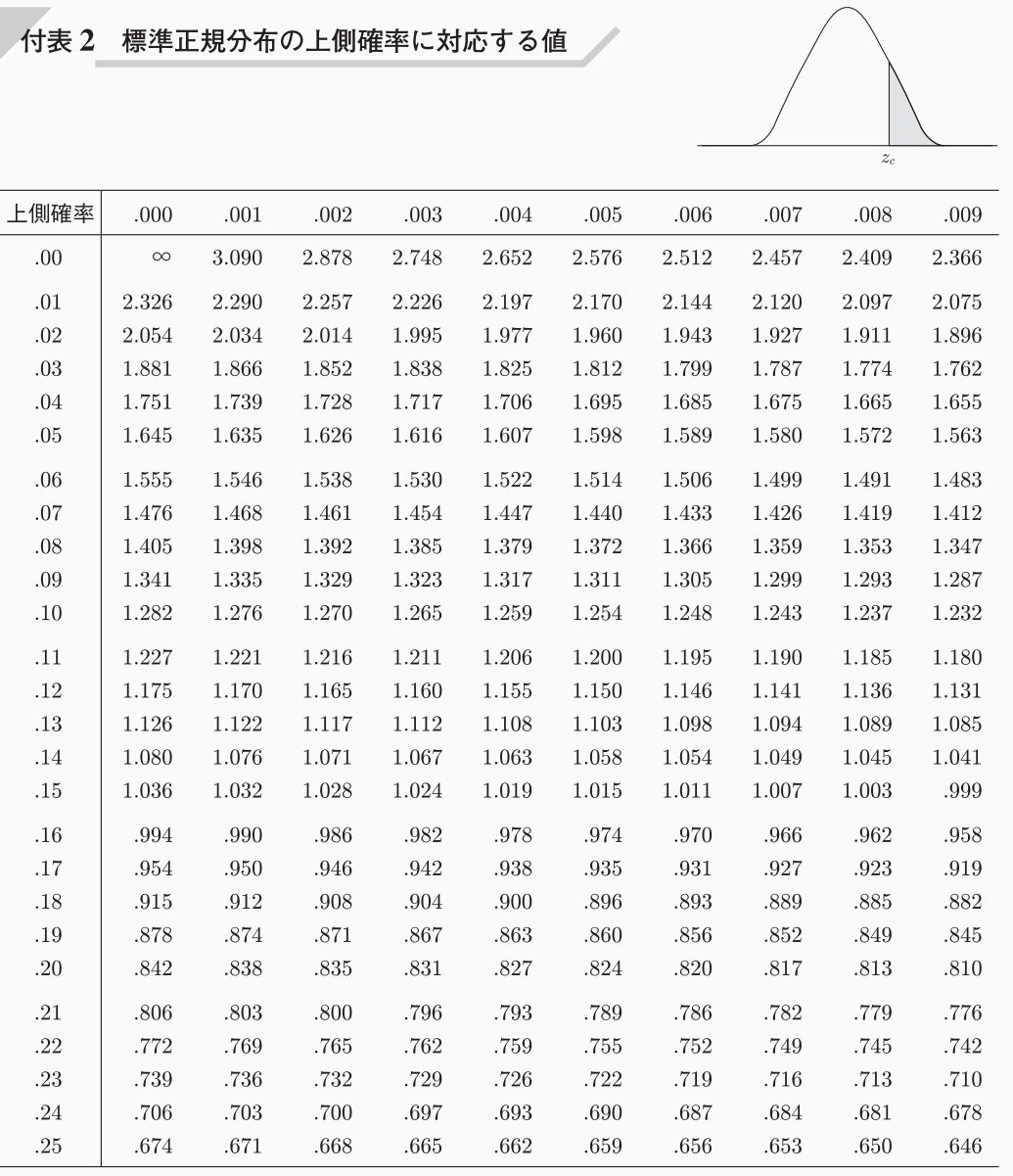
下図の標準正規分布表から、両側検定の有意水準\(\alpha = 0.05\)の点を求めます。
(両側検定なので、片側0.025ずつとなります)
よって、\(z_{0.025} = 1.96\)であり、棄却域は、\( z < -1.96,1.96<z\)となります。
4.判定
データから求めた検定統計量は、\(z=3.75 > 1.96\)となることから、検定統計量zは棄却域に入り、帰無仮説は棄却されます。
5.結論
帰無仮説が棄却されたため、サンプルの母平均は300ppmではなく、すなわち製品\(A\)の不純物濃度は変化していると言えます。
母平均の検定(母分散が未知の場合)
次は、母分散が未知の場合を考えてみましょう。
例えば、母集団となるデータを自社で保有していない場合、母分散を知る方法が無いので、このケースに該当します。
【例題②】購入品(樹脂)のスペック調査
ガラス転移温度\(T_g\)が100℃の樹脂\(A\)の継続的な購入を検討しています。
ガラス転移温度の平均値\(\mu_0\)が本当に100℃あるのか、検定してみましょう。
サンプル提供(n=20)を依頼し、分析して確かめたところ、平均\(\overline{x}=99\)℃、標本分散が\(s^2 = 3^2\)でした。
ちなみに、標本分散は、偏差平方和をn-1で割ったものです。
$$s^{2}=\frac{1}{n-1}\sum ^{n}_{i=1}\left( x_{i}-\overline{x}\right) ^{2}$$
それでは、検定の手順に従い、例題を解いていきましょう。
樹脂\(A\)は、まだ購入検討段階であり、データが無いため母分散は不明です。(メーカーが開示してくれれば別ですが)
よって、母分散が未知の場合の母平均の検定ですので、「t検定」を行います。
t検定では、検定統計量tがt分布に従います。(t分布表を参照します)
1.仮説の設定
帰無仮説\(H_0 \):\(\mu = 100\) ℃(サンプルの母平均も100℃である)
対立仮説\(H_1 \):\(\mu < 100\) ℃(サンプルの母平均は100℃未満である)
ガラス転移温度は、100℃以上であれば問題ないと考えることができるため、今回は「片側検定」とします。
もし、ガラス転移温度が高すぎても良くない場合は、両側検定を行います。
2.検定統計量の算出
母分散が未知であるため、検定統計量tを使用します。
$$\begin{aligned}t&=\frac{\overline{x}-\mu _{0}}{\frac{s }{\sqrt{n}}}\\[5pt]
&=\frac{99-100}{\frac{3}{\sqrt{20}}}\\[5pt]
&=-1.49\end{aligned}$$
3.棄却域の設定
有意水準は、\(\alpha = 0.05\left( 5\% \right)\)とします。
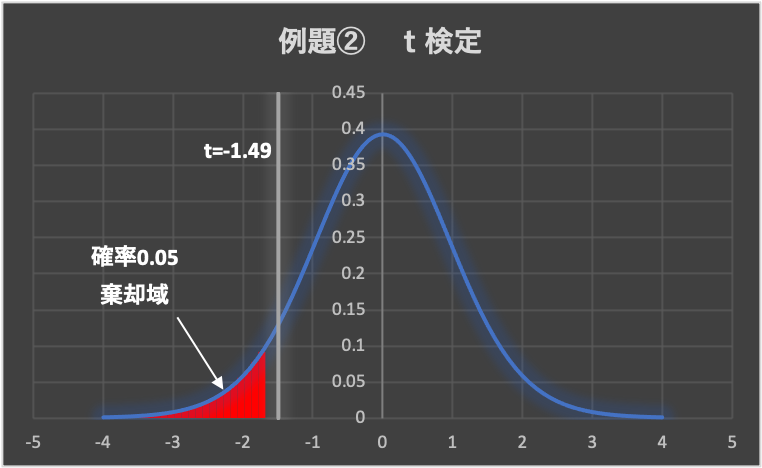
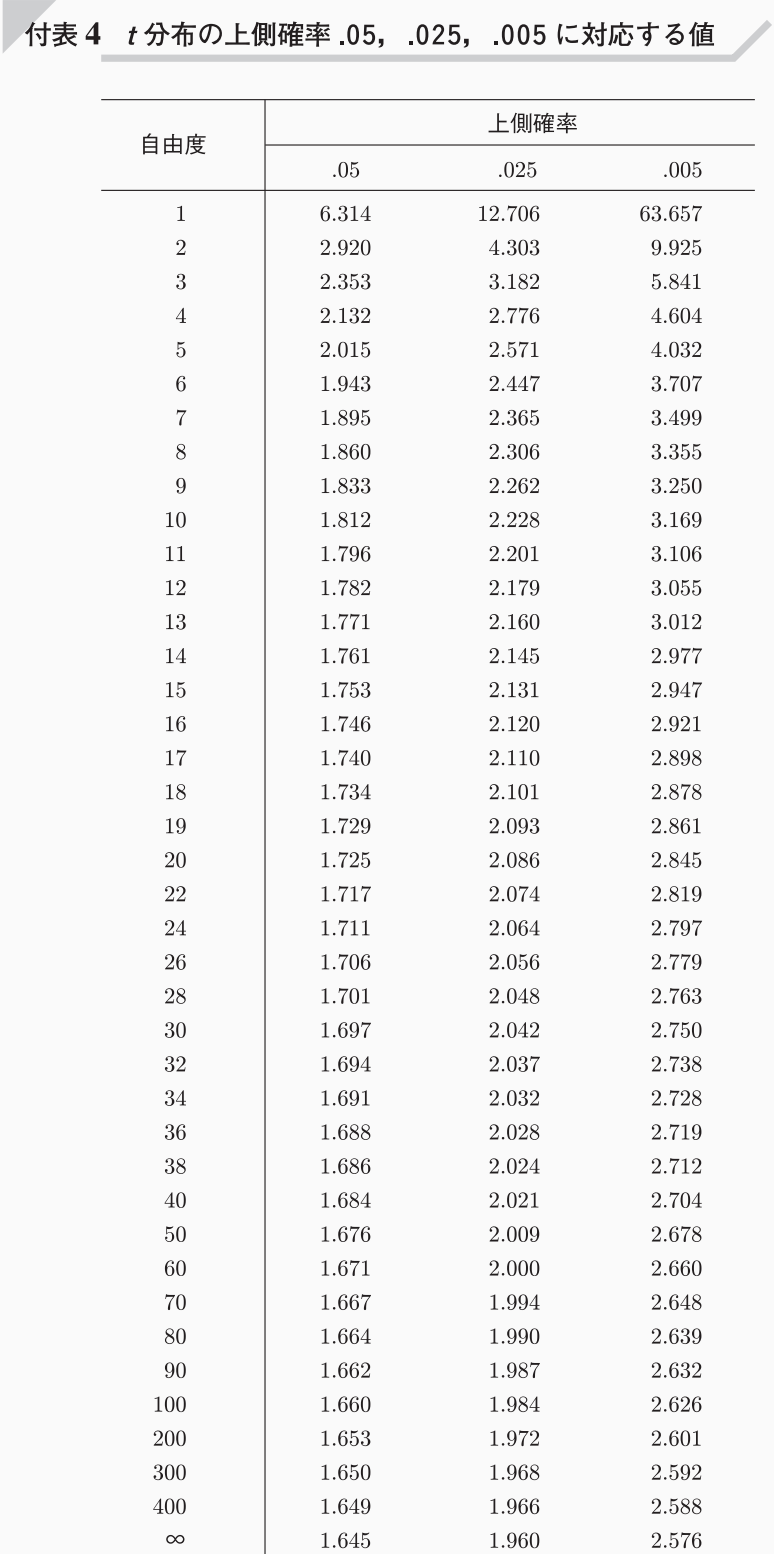
下図のt分布表から、片側検定の有意水準\(\alpha = 0.05\)の点を求めます。
よって、\(t_{0.05}\left( n-1=19 \right) =1.729\)であり、棄却域は、\( t < -1.729\)となります。
ガラス転移温度が低い場合のみ棄却しますので、棄却域はマイナス側だけになります。
4.判定
データから求めた検定統計量は、\(t=-1.49 > -1.729\)となることから、検定統計量tは棄却域に入らず、帰無仮説が採択されます。
5.結論
帰無仮説が採択されたため、購入する樹脂のガラス転移温度\(T_g\)は、100℃より低いとは言えない。という結論になります。
平均値の差の検定(独立な2群:母分散が既知の場合)
続いて、独立な2群の平均値の差を検定しましょう。
ある母集団Aと母集団Bの平均値が等しいかどうかを検定します。
独立な2群というのは、母集団Aと母集団Bの間に相関関係が無いということです。
例えば、母集団Aの数値が大きい時に、母集団Bが大きくなる傾向がある場合、それは独立ではなく、後述する「対応のある2群」と見なします。
それでは例題を見てみましょう。
【例題③】原料メーカーの変更
量産化している製品\(A\)の原料を、\(B\)社から\(C\)社に変更しました。
原料メーカーを\(B\)社から\(C\)社に変更した際、製品\(A\)の不純物濃度が変わっているかどうかを検定してみます。
\(B\)社の原料を使って生産した製品\(A\)の不純物濃度の平均値が\(\mu_B = 300\)ppm、母分散が\(\sigma_B^2 = 8^2\)であったとき、\(C\)社の原料を使って生産した製品\(A\)の不純物濃度の平均値が\(\mu_C = 303\)ppm、母分散が\(\sigma_C^2 = 4^2\)でした。
ここで、\(B\)社と\(C\)社共にデータ数は100\(( n_{B}=n_{C}= 100)\)とします。
(量産化製品\(A\)のデータ数は多いため、母集団と見なします。)
それでは、検定の手順に従い、例題を解いていきましょう。
例題③は、母分散が既知の場合の平均値の差の検定ですので、「z検定」です。
よって、検定統計量zが正規分布に従います。(正規分布表を参照します)
1.仮説の設定
帰無仮説\(H_0 \):\(\mu_B=\mu_C\)(2つの母平均は等しい)
対立仮説\(H_1 \):\(\mu_B \neq \mu_C\)(2つの母平均は等しくない)
大きくても小さくても差があれば、「変化あり」ですので「両側検定」です。
2.検定統計量の算出
母分散が既知であるため、検定統計量zを使用します。
$$\begin{aligned}z&=\frac{\mu _{B}-\mu_{C}}{\sqrt{\frac{\sigma_{B} ^{2}}{n_{B}}+\frac{\sigma _{C}^{2}}{n_{C}}}}\\[5pt]
&=\frac{300-303}{\sqrt{\frac{8^{2}}{100}+\frac{4^{2}}{100}}}\\[5pt]
&=-3.35\end{aligned}$$
3.棄却域の設定
有意水準は、\(\alpha = 0.05\left( 5\% \right)\)とします。
例題①にある正規分布表から、両側検定の有意水準\(\alpha = 0.05\)の点を求めます。
(両側検定なので、片側0.025ずつとなります)
よって、\(z_{0.025} = 1.96\)であり、棄却域は、\( z < -1.96,1.96<z\)となります。
4.判定
データから求めた検定統計量は、\(z=−3.35 < -1.96\)となることから、検定統計量zは棄却域に入り、帰無仮説は棄却されます。
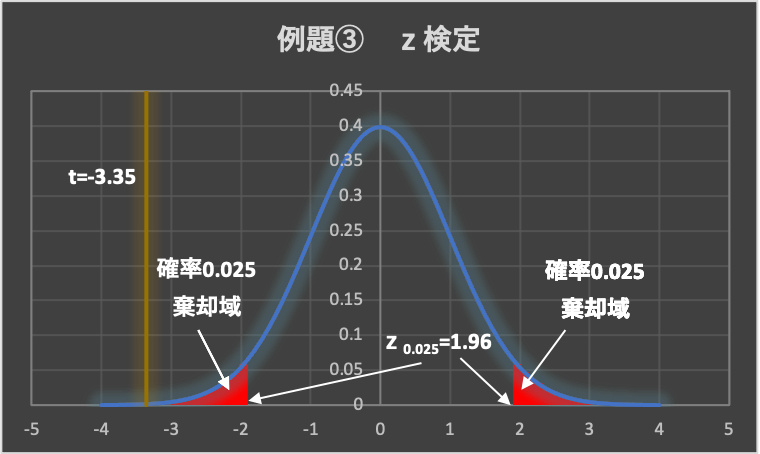
5.結論
帰無仮説が棄却されたため、2つの母平均は等しくないと言えます。
すなわち、原料メーカーが\(B\)社から\(C\)社に変わったことで、製品\(A\)の不純物濃度は変化していると言えます。
平均値の差の検定(独立な2群:母分散が未知の場合①)
次は、母分散が未知の場合を考えます。
ラボ実験や試作機における試作では、データ数が少なく、母集団と見なすことができません。
よって、母分散が未知であるとし、検定を行いましょう。
【例題④】試作機における原料メーカーの変更(t検定)
量産化前の試作品\(D\)の原料を、\(E\)社から\(F\)社に変更しました。
原料メーカーを\(E\)社から\(F\)社に変更した際、試作品\(D\)の不純物濃度が変わっているかどうかを検定してみます。
\(E\)社の原料を使って生産した試作品\(D\)の不純物濃度の平均値が\(\overline{x}_E = 300\)ppm、標本分散が\(s_E^2 = 16^2\)であったとき、\(F\)社の原料を使って生産した試作品\(D\)の不純物濃度の平均値が\(\overline{x}_F = 303\)ppm、標本分散が\(s_F^2 = 14^2\)でした。
ここで、\(E\)社品と\(F\)社品共にデータ数は10\(( n_{E}=n_{F}= 10)\)とします。
また、2つの標本分散\(s_E^2\)と\(s_F^2\)は等しいと見なせるとします。※
※本来は、分散が等しいかどうかを別途検定する必要があります。(後述します)
それでは、検定の手順に従って、例題を解いていきましょう。
例題④は、母分散が未知で、2つの標本分散が等しいと見なせるので「t検定」となります。
よって、検定統計量tがt分布に従います。(t分布を参照します)
1.仮説の設定
帰無仮説\(H_0 \):\(\mu_E=\mu_F\)(2つの母平均は等しい)
対立仮説\(H_1 \):\(\mu_E \neq \mu_F\)(2つの母平均は等しくない)
大きくても小さくても差があれば、「変化あり」ですので「両側検定」です。
2.検定統計量の算出
母分散が未知で、2つの標本分散が等しいと見なせるため、下記の検定統計量tを使用します。
$$\begin{aligned}t&=\frac{x_{E}-x_{F}}{s\sqrt{\frac{1}{n_{E}}+\frac{1}{n_{F}}}}\end{aligned}$$
ここで、標本の標準偏差\(s\)を下記のように求めます。
$$\begin{aligned}s&=\sqrt{\frac{s_{E}^{2}\left( n_{E}-1\right) +s_F^{2}\left( n_{F}-1\right) }{n_{E}+n_{F}-2}}\\[5pt]
&=\sqrt{\frac{16^2\left(10-1\right)+14^2\left(10-1\right)}{10+10-2}}\\[5pt]
&=15.03\end{aligned}$$
よって、検定統計量tを計算すると、
$$\begin{aligned}t&=\frac{x_{E}-x_{F}}{s\sqrt{\frac{1}{n_{E}}+\frac{1}{n_{F}}}}\\[5pt]
&=\frac{300-303}{15.03\sqrt{\frac{1}{10}+\frac{1}{10}}}\\[5pt]
&=-0.45\end{aligned}$$
となります。
3.棄却域の設定
有意水準は、\(\alpha = 0.05\left( 5\% \right)\)とします。
例題②のt分布表から、両側検定の有意水準\(\alpha = 0.05\)の点を求めます。
(両側検定なので、片側0.025ずつとなります)
よって、\(t_{0.025}\left( n_E+n_F-2=18 \right) =2.101\)であり、棄却域は、\( t < -2.101, 2.101 < t\)となります。
4.判定
データから求めた検定統計量は、\(t=-0.45 > -2.101\)となることから、検定統計量tは棄却域に入らず、帰無仮説が採択されます。
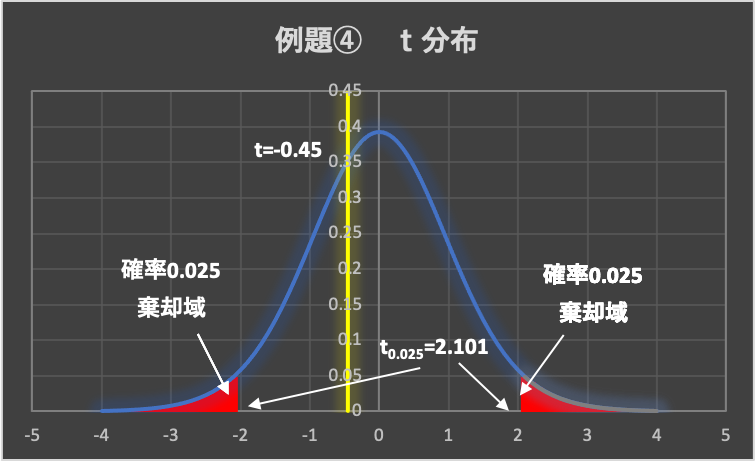
5.結論
帰無仮説が採択されたため、原料メーカーを変更しても、試作品\(D\)の不純物濃度は変わっているとは言えない。という結論になります。
平均値の差の検定(独立な2群:母分散が未知の場合②)
次は、母分散が未知で、かつ2つの標本分散が等しくない場合の検定について考えましょう。
この検定は、一般にWelchの検定と呼ばれています。
それでは、例題を見ていきましょう。
【例題⑤】試作機における原料メーカーの変更(Welchの検定)
量産化前の試作品\(D\)の原料を、\(E\)社から\(F\)社に変更しました。
原料メーカーを\(E\)社から\(F\)社に変更した際、試作品\(D\)の不純物濃度が変わっているかどうかを検定してみます。
\(E\)社の原料を使って生産した試作品\(D\)の不純物濃度の平均値が\(\overline{x}_E = 300\)ppm、標本分散が\(s_E^2 = 12^2\)であったとき、\(F\)社の原料を使って生産した試作品\(D\)の不純物濃度の平均値が\(\overline{x}_F = 310\)ppm、標本分散が\(s_F^2 = 5^2\)でした。
ここで、\(E\)社品と\(F\)社品共にデータ数は10\(( n_{E}=n_{F}= 10)\)とします。
また、2つの標本分散\(s_E^2\)と\(s_F^2\)は等しくないと見なせるとします。※
※本来は、分散が等しいかどうかを別途検定する必要があります。(後述します)
それでは、検定の手順に従って、例題を解いていきましょう。
例題⑤は、母分散が未知で、2つの標本分散が等しくないと見なせるので「Welchの検定」となります。
t検定と同様、検定統計量tがt分布に従いますが、自由度を特殊な計算で求めます。
1.仮説の設定
帰無仮説\(H_0 \):\(\mu_E=\mu_F\)(2つの母平均は等しい)
対立仮説\(H_1 \):\(\mu_E \neq \mu_F\)(2つの母平均は等しくない)
大きくても小さくても差があれば、「変化あり」となりますので「両側検定」です。
2.検定統計量の算出
母分散が未知で、2つの標本分散が等しくないため、下記の検定統計量tを使用します。
$$\begin{aligned}t&=\frac{\mu_{E}-\mu_{F}}{\sqrt{\frac{s_E^2}{n_{E}}+\frac{s_F^2}{n_{F}}}}\\[5pt]
&=\frac{300-310}{\sqrt{\frac{12^2}{10}+\frac{5^2}{10}}}\\[5pt]
&=-2.43\end{aligned}$$
ここで、自由度\(v\)を下記の通り求めます。
$$\begin{aligned}v&=\frac{( \frac{s_E^2}{n_E}+\frac{s_F^2}{n_F}) ^2}{\frac{s_E^4}{n_E^2(n_E-1)}+\frac{s_F^4}{n_F^2(n_F-1)}}\\[5pt]
&=\frac{(\frac{12^2}{10}+\frac{5^2}{10}) ^2}{\frac{12^4}{100(10-1)}+\frac{5^4}{100(10-1)}}\\[5pt]
&=12.0\end{aligned}$$
よって、自由度\(v=12\)となります。
3.棄却域の設定
有意水準は、\(\alpha = 0.05\left( 5\% \right)\)とします。
例題②のt分布表から、両側検定の有意水準\(\alpha = 0.05\)の点を求めます。
(両側検定なので、片側0.025ずつとなります)
よって、\(t_{0.025}\left( v=12 \right) =2.179\)であり、棄却域は、\( t < -2.179, 2.179 < t\)となります。
4.判定
データから求めた検定統計量は、\(t=-2.43 < -2.179\)となることから、検定統計量tは棄却域に入り、帰無仮説は棄却されます。
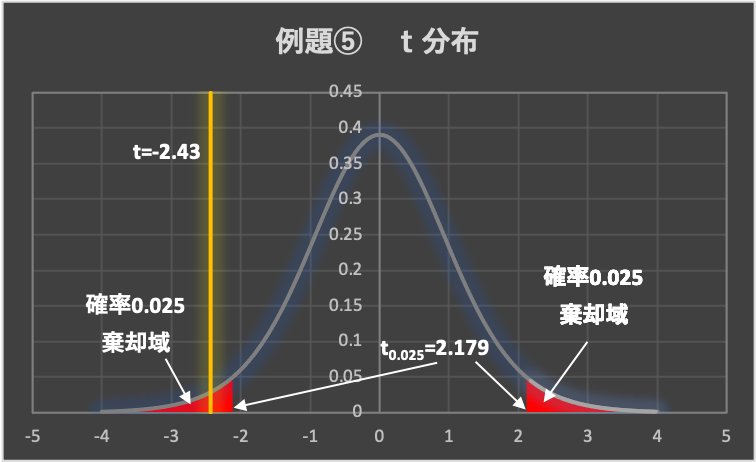
5.結論
帰無仮説が棄却されたため、2つの母平均は等しくないと言えます。
すなわち、原料メーカーが\(E\)社から\(F\)社に変わったことで、試作品\(D\)の不純物濃度は変化していると言えます。
平均値の差の検定(対応のある2群)
これまで、例題③〜⑤では、独立な2群(相関が無い2群)について検定を行ってきました。
今回は、対応のある2群の平均値の差の検定を行います。
【例題⑥】オンライン濃度計の測定値ズレ
ある物質の濃度を測定するオンライン濃度計があります。
新型を購入したため、旧型との測定値のズレがないか確かめるため、平均値検定を行います。
新型と旧型で同時に同サンプルの測定を行い、測定値を下表にまとめました。
| No. | 新型 mg/L | 旧型 mg/L | 差(d) mg/L |
| 1 | 3.8 | 3.2 | 0.6 |
| 2 | 3.0 | 3.0 | 0.0 |
| 3 | 3.6 | 3.2 | 0.4 |
| 4 | 2.8 | 1.8 | 1.0 |
| 5 | 3.4 | 2.9 | 0.5 |
差\(d\)の平均値は、\(\overline{d} = 0.5\)で、差\(d\)の標本分散は、\(s^2=0.13\)でした。
$$s^{2}=\frac{1}{n-1}\sum ^{n}_{i=1}\left( d_{i}-\overline{d}\right) ^{2}$$
同時に同サンプルを測定したため、新型と旧型の測定値には相関があると考えられます。
よって、対応のある2群の「t検定」を行います。
それでは、検定の手順に従って、例題を解いていきましょう。
1.仮説の設定
帰無仮説\(H_0 \):\(\overline{d}=0\)(差\(d\)の母平均は0である)
対立仮説\(H_1 \):\(\overline{d} \neq 0\) (差\(d\)の母平均は0ではない)
プラスでもマイナスでも差があれば、「0ではない」となりますので「両側検定」です。
2.検定統計量の算出
対応のある2群の平均値の検定は、下記の検定統計量tを使用します。
$$\begin{aligned}t&=\frac{\overline{d}}{\sqrt{\frac{s^2}{n}}}\\[5pt]
&=\frac{0.5}{\sqrt{\frac{0.13}{5}}}\\[5pt]
&=3.1\end{aligned}$$
3.棄却域の設定
有意水準は、\(\alpha = 0.05\left( 5\% \right)\)とします。
例題②のt分布表から、両側検定の有意水準\(\alpha = 0.05\)の点を求めます。
(両側検定なので、片側0.025ずつとなります)
よって、\(t_{0.025}\left( n-1=4 \right) =2.776\)であり、棄却域は、\( t < -2.776, 2.776 < t\)となります。
4.判定
データから求めた検定統計量は、\(t=3.1 > 2.776\)となることから、検定統計量tは棄却域に入り、帰無仮説は棄却されます。
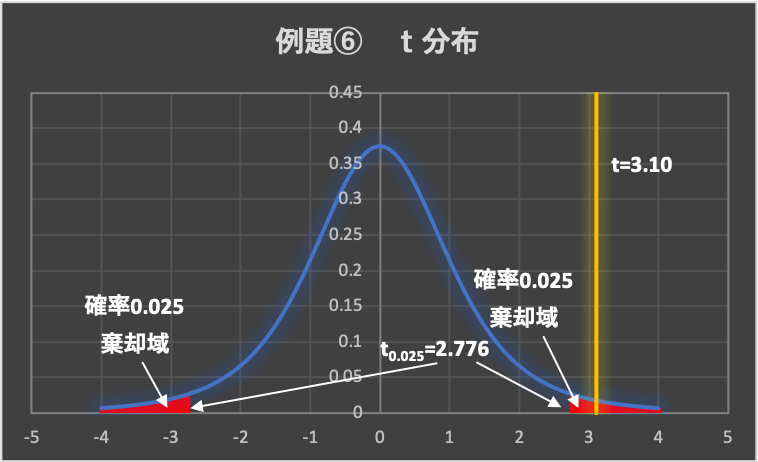
5.結論
帰無仮説が棄却されたため、差\(d\)の平均値は0ではないと言えます。
すなわち、新型と旧型のオンライン濃度計では、測定値に有意な差があると言えます。
母分散の比の検定(F検定)
独立な2群の平均値の差の検定(例題④、⑤)では、分散が等しい場合は「t検定」、分散が異なる場合は「Welchの検定」を行いました。
しかし、分散が等しいかどうかの判断についても、平均値と同様に「母分散の比の検定(F検定)」を行う必要があります。
例題④、⑤について母分散の比の検定を行ってみましょう。
【例題⑦】例題④、⑤の母分散の比の検定
(1)例題④の母分散の比の検定
標本分散が\(s_E^2 = 16^2\)、\(s_F^2 = 14^2\)で、データ数は共に10\(( n_{E}=n_{F}= 10)\)です。
(2)例題⑤の母分散の比の検定
標本分散が\(s_E^2 = 12^2\)、\(s_F^2 = 5^2\)で、データ数は共に10\(( n_{E}=n_{F}= 10)\)です。
それでは、検定の手順に従い検定を行っていきます。
(1)例題④の母分散の比の検定
1.仮説の設定
帰無仮説\(H_0 \):\(\sigma_E^2=\sigma_F^2\) (2つの母分散は等しい)
対立仮説\(H_1 \):\(\sigma_E^2 > \sigma_F^2\) (\(\sigma_E^2\)の方が\(\sigma_F^2\)より大きい)
今回、\(\sigma_E^2\)が、\(\sigma_F^2\)より大きいかどうかを検定するため、「片側検定」とします。
2.検定統計量の算出
母分散の比の検定は、下記の検定統計量\(F\)を使用します。
$$\begin{aligned}F&=\frac{s_E^2}{s_F^2}\\[5pt]
&=\frac{16^2}{14^2}\\[5pt]
&=1.31\end{aligned}$$
※対立仮説\(H_1 \)で大きいと仮定した標本分散\(s_E^2\)を分子に持ってきます。
3.棄却域の設定
有意水準は、\(\alpha = 0.05\left( 5\% \right)\)とします。
下図のF分布表から、片側検定の有意水準\(\alpha = 0.05\)の点を求めます。
よって、\(F_{0.05}\left(n_E-1=9,n_F-1=9 \right) =3.18\)であり、棄却域は、\(F > 3.18\)となります。
4.判定
データから求めた検定統計量は、\(F=1.31 < 3.18\)となることから、検定統計量Fは棄却域に入らず、帰無仮説が採択されます。
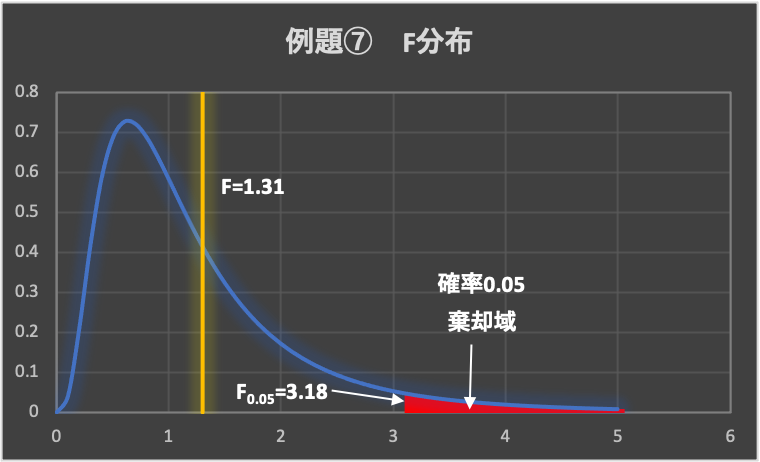
5.結論
帰無仮説が採択されたため、「母分散に有意な差があるとは言えない。」という結論になります。
(2)例題⑤の母分散の比の検定
(1)と同様な手順で検定を行いましょう。
1.仮説の設定
帰無仮説\(H_0 \):\(\sigma_E^2=\sigma_F^2\) (2つの母分散は等しい)
対立仮説\(H_1 \):\(\sigma_E^2 > \sigma_F^2\) (\(\sigma_E^2\)の方が\(\sigma_F^2\)より大きい)
今回、\(\sigma_E^2\)が、\(\sigma_F^2\)より大きいかどうかを検定するため、「片側検定」とします。
2.検定統計量の算出
母分散の比の検定は、下記の検定統計量Fを使用します。
$$\begin{aligned}F&=\frac{s_E^2}{s_F^2}\\[5pt]
&=\frac{12^2}{5^2}\\[5pt]
&=5.76\end{aligned}$$
※対立仮説\(H_1 \)で大きいと仮定した標本分散\(s_E^2\)を分子に持ってきます。
3.棄却域の設定
有意水準は、\(\alpha = 0.05\left( 5\% \right)\)とします。
下図のF分布表から、片側検定の有意水準\(\alpha = 0.05\)の点を求めます。
よって、\(F_{0.05}\left(n_E-1=9,n_F-1=9 \right) =3.18\)であり、棄却域は、\(F > 3.18\)となります。
4.判定
データから求めた検定統計量は、\(F=5.76 > 3.18\)となることから、検定統計量\(F\)は棄却域に入り、帰無仮説は棄却されます。
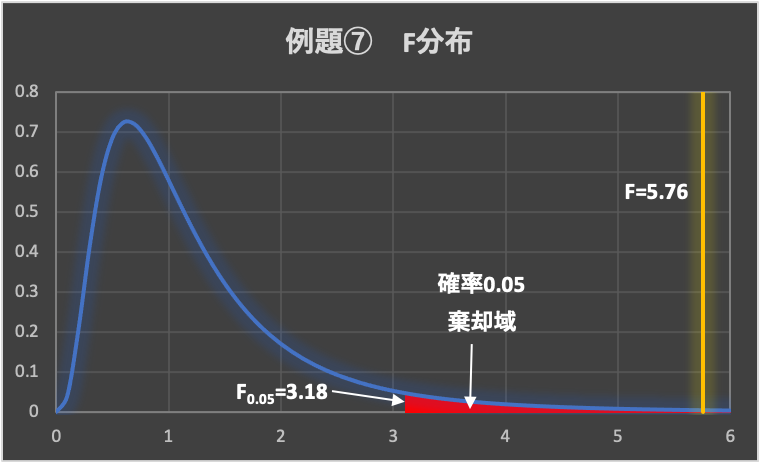
5.結論
帰無仮説が棄却されたため、\(\sigma_E^2\)の方が\(\sigma_F^2\)より大きいと言えます。
すなわち、母分散に有意な差がある(\(\sigma_E^2\)の方が\(\sigma_F^2\)より大きい)と言えます。
無相関検定(t検定)
ようやく最後の例題です。
「相関があるかどうか」の判断についても「t検定」を行うことができます。
それでは、例題を見ていきましょう。
【例題⑧】試作品の製造条件と品質の相関関係
試作品\(G\)の製造条件\(H\)を変更すると、品質\(I\)に大きく影響すると考えられています。
そこで、製造条件\(H\)を様々に変化させて20回(n=20)の試作を行い、品質\(I\)との相関を確認しました。
すると、相関係数\(r =0. 66\)という結果となりました。
この結果から、”中程度の相関がある”ことがわかりますが、これがたまたま(偶然)なのか、本当に相関があるのかを検定をしたいと思います。
それでは、検定の手順に従って、例題を解いていきましょう。
1.仮説の設定
帰無仮説\(H_0 \):\(\rho=0\) (母相関係数が0である)
対立仮説\(H_1 \):\(\rho \neq 0\) (母相関係数が0ではない)
プラスでもマイナスでも差があれば、「0ではない」となりますので「両側検定」です。
2.検定統計量の算出
無相関検定は、下記の検定統計量tを使用します。
$$\begin{aligned}t&=\frac{r}{\sqrt{1-r^{2}}}\times \sqrt{N-2}\\[5pt]
&=\frac{0.66}{\sqrt{1-0.66^{2}}}\times \sqrt{20-2}\\[5pt]
&=3.73\end{aligned}$$
3.棄却域の設定
有意水準は、\(\alpha = 0.05\left( 5\% \right)\)とします。
例題②のt分布表から、両側検定の有意水準\(\alpha = 0.05\)の点を求めます。
(両側検定なので、片側0.025ずつとなります)
よって、\(t_{0.025}\left( n-2=18 \right) =2.101\)であり、棄却域は、\( t < -2.101, 2.101 < t\)となります。
4.判定
データから求めた検定統計量は、\(t=3.73 > 2.101\)となることから、検定統計量tは棄却域に入り、帰無仮説は棄却されます。
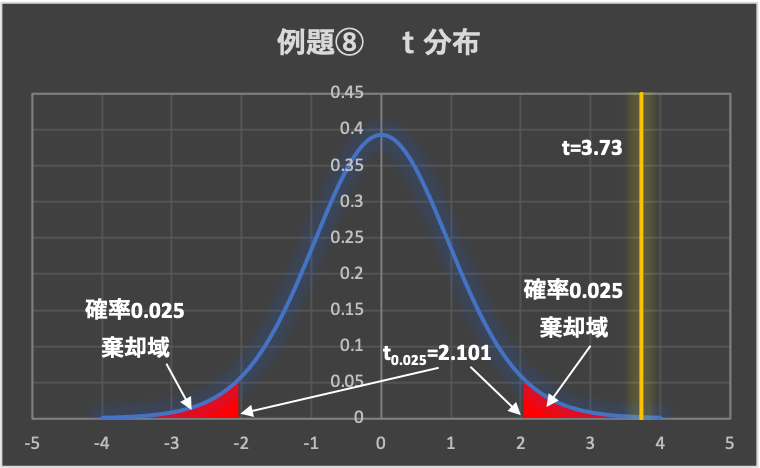
5.結論
帰無仮説が棄却されたため、母相関係数は0ではないと言えます。
すなわち、相関係数は有意であるという結論になります。
参考文献
1.心理統計学の基礎(有斐閣アルマ)統計検定2級〜準1級レベル
本記事では、この本を大いに参考にさせてもらいました。
初級から中級レベルに運んでくれるような、非常に詳しい解説があります。
特に「検定力分析によるサンプルサイズの決定」、「線形モデルの基礎」の解説が好きです。
入門書(基本統計学(第3版)など)を読んだ後に、ぜひ挑戦してみて下さい。
-

-
【書評】心理統計学の基礎 難易度と読み方を解説!
続きを見る
統計検定2級を受験する際に、最もお世話になった本です。
非常にわかりやすく書かれています。特に、レイアウトが秀逸で読みやすいのが良いです。
例題を作成する上で参考にしました。
製造現場で品質管理をする方にオススメです。


 引用
引用