
化学プラント向けのPID制御を解説して欲しいな。
こんなお悩みを解決します。
どうも。こんにちは。
ケミカルエンジニアのこーしです。
本日は、「化学系のためのPID制御」についてわかりやすく解説していきます。
この記事を読むことで、化学プラントにおけるPID制御が理解できるようになります。
本記事の内容
- PID制御とは
- PID制御の基礎式
- PIDパラメータの目安
この記事を書いた人
 こーし(@mimikousi)
こーし(@mimikousi)
PID制御とは
PID制御は、最も広く使われている制御方式です。
化学プラントも、基本的にPID制御を使っています。
PID制御では、設定値SVと測定値PVの差分(偏差)に、比例・積分・微分の3つを組み合わせた演算を行い、操作量MVを決定します。
比例制御(Proportional control)、積分制御(Integral control)、微分制御(Derivative control)のそれぞれ頭文字をとって、PID制御と呼ばれています。
| 用語 | 略称 | 英語 |
| 設定値 | SV | Setting Value |
| 測定値 | PV | Process Variable |
| 操作量 | MV | Manipulated Value |
比例制御とは
比例制御は、偏差 \(e\left( t\right) \)の大きさに比例して操作量MVを変化させます。
※偏差 \(e\left( t\right) =SV\left( t\right) -PV\left( t\right)\)
比例定数を比例ゲイン\(K_{p}\)とおくと、比例制御における入出力の関係は、下式のように表せます。
$$MV\left( t\right) =K_{p}e\left( t\right) \tag{1}$$
簡便のため偏差 \(e\left( t\right) =E\)(定数)と仮定すると、下図のように操作量MVは、偏差の\(K_{p}\)倍となります。

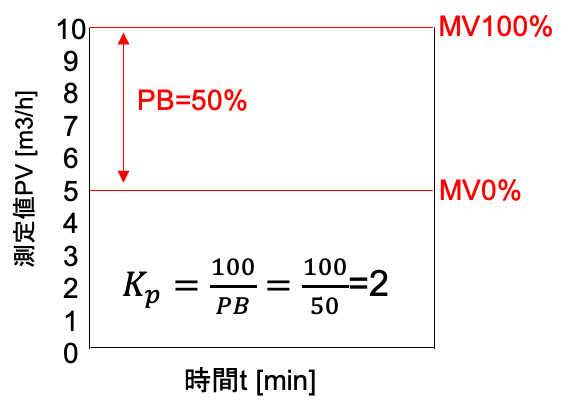
続いて、比例帯(PB:Proportional Band)についても解説しておきます。
比例ゲインと比例帯の関係は下式の通りです。
$$K_{p}=\frac{100}{PB} \tag{2}$$
比例帯とは、操作量MV(0〜100%)が対応する範囲が制御量の検出器レンジに対して何%なのかを表す指標です。
わかりやすいように、流量制御を例に図解してみました。
(1)、(2)式と下図からわかるように、比例帯が小さいと操作量MVが大きく動きます。

比例制御の特徴
比例制御だけでは、どんなに時間が経っても設定値SVと測定値PVが一致することはありません。
どんなに時間が経っても消えないSV値とPV値の差を「定常偏差(オフセット)」といいます。
オフセットを消すためには、積分制御を組み合わせる必要があります。
積分制御とは
積分制御は、偏差 \(e\left( t\right) \)を積分した値に比例して操作量MVを変化させます。
比例定数を積分ゲイン\(K_{i}\)とおくと、積分制御における入出力の関係は、下式のように表せます。
$$MV\left( t\right) =K_{i}\int e\left( t\right) dt \tag{3}$$
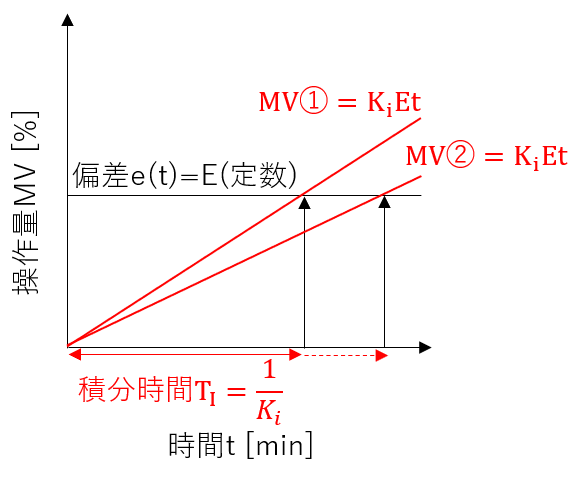
続いて、積分時間\(T_{I}\)についても解説しておきます。
簡便のため偏差 \(e\left( t\right) =E\)(定数)と仮定すると、(3)式は下式のように変形できます。
$$MV\left( t\right) =K_{i}Et \tag{4}$$
ここで、\(t=T_{I}=\dfrac{1}{K_{i}}\)の時、積分制御の操作量MVが偏差 \(e\left( t\right) =E\)(定数)と一致することがわかります。
この時間\(t\)を積分時間\(T_{I}\)と呼び、\(T_{I}=\dfrac{1}{K_{i}}\)となります。
つまり、積分制御の操作量MVが偏差と同じ値になるまでの時間が積分時間\(T_{I}\)であり、\(T_{I}\)が大きいほど、操作量MVは小さく動きます。(上図MV②のように傾きが小さくなります)
積分時間\(T_{I}\)を用いて、(3)式を変形すると下式となります。
$$MV\left( t\right) =\frac{1}{T_{I}}\int e\left( t\right) dt \tag{5}$$
積分ゲイン\(K_{i}\)と積分時間\(T_{I}\)のどちらを使うかはメーカによって異なりますので、注意しましょう。
積分制御の特徴
定常偏差(オフセット)がある場合、比例制御だけだと操作量が一定で変化しなくなるため、オフセットが消えないという問題がありました。
しかし、積分制御を加えると、定常偏差がどんどん足されていく(積分される)ため、上図のように時間とともに操作量MVが大きくなり、オフセットを打ち消してくれます。
微分制御とは
微分制御は、偏差 \(e\left( t\right) \)を微分した値に比例して操作量MVを変化させます。
比例定数を微分ゲイン\(K_{d}\)とおくと、微分制御における入出力の関係は、下式のように表せます。
$$MV\left( t\right) =K_{d}\frac{de\left( t\right) }{dt}\tag{6}$$
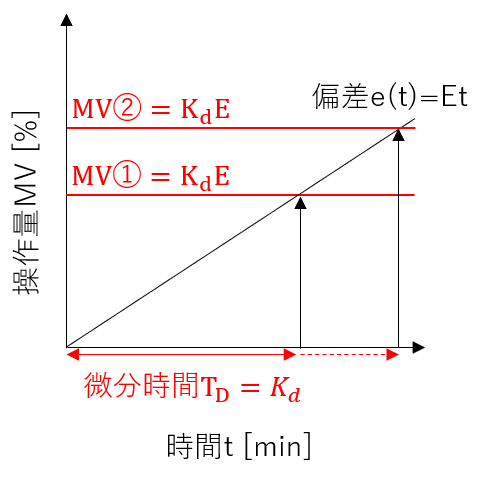
続いて、微分時間\(T_{D}\)についても解説しておきます。
偏差 \(e\left( t\right) \)が傾き一定で変化していると仮定すると \(e\left( t\right) =Et\)となり、(6)式は下式のように変形できます。
$$MV\left( t\right) =K_{d}\frac{d\left( Et\right) }{dt}=K_{d}E\tag{7}$$
よって、\(t={K_{d}}\)の時、微分制御の操作量MVと偏差 \(e\left( t\right) =Et\)が一致することがわかります。
この時間を微分時間\(T_{D}\)と呼び、\(T_{D}=K_{d}\)となります。
上図からわかるように、微分時間\(T_{D}\)が大きいほど、微分制御の操作量MVが大きく動きます。(MV①→MV②)
微分制御の特徴
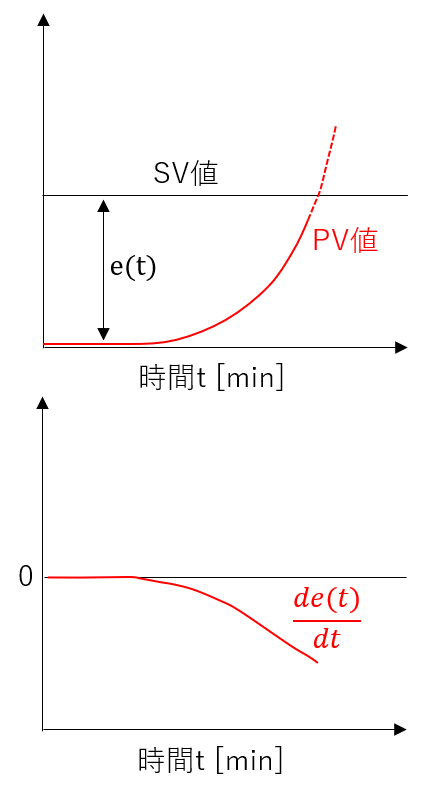
微分制御を加えると、設定値の変更に素早く応答してくれます。
つまり、偏差\(e\left( t\right) \)の変化に比例して、操作量が大きくなります。
また、比例と積分制御だけだとPV値がSV値を行き過ぎる現象(オーバーシュート)が起こりますが、微分制御はPV値とSV値が近づいていくと、偏差\(e\left( t\right) \)が小さくなり、(6)式がマイナスとなって、ブレーキの役割を果たします。(下図を参照)
ただし、微分制御はノイズを拡大しやすいのが欠点です。
PID制御の基礎式【重要!】
これから取り扱うコントローラの「PID制御の基礎式」を把握しておくことは、とても重要です。
なぜなら、メーカによってパラメータの中身が全然違うからです。
例えば、パラメータとして比例ゲイン\(K_{p}\)を使うのか、比例帯\(PB\)を使うのかでパラメータの大小が正反対となってしまいます。
よって、まず始めに「PID制御の基礎式」をよく確認し、パラメータや単位は何かを把握しましょう。
PID制御の代表的な基礎式を3例あげておきます。
基礎式①
比例帯\(PB\) [%]
積分時間\(T_{I}\) [秒]
微分時間\(T_{D}\) [秒]
基礎式②
比例ゲイン\(K_{p}\) [-]
積分時間\(T_{I}\) [秒]
微分時間\(T_{D}\) [秒]
基礎式③
比例ゲイン\(K_{p}\) [-]
積分ゲイン\(K_{i}\) [-]
微分ゲイン\(K_{d}\) [-]
特に、制御の強さが正反対になってしまう下記のペアには要注意です。
- 比例ゲイン\(K_{p}\)と比例帯\(PB\)
- 積分ゲイン\(K_{i}\)と積分時間\(T_{I}\)
PIDパラメータの目安
化学プラントにおけるPIDパラメータの目安について下表にまとめました。
様々な教科書や文献を調査し、最終的に自分が担当するプロセスに当てはめてみた結果になります。
| 流量 制御 |
液面 制御 |
圧力 制御 (積分系) |
圧力 制御 (定常系) |
温度 制御 |
成分 制御 |
|
| 比例帯 \(PB \%\) |
100〜500 | 10~100 | 10~100 | 100〜500 | 10~100 | 100~1000 |
| 比例ゲイン\(K_{p}\) | 0.2〜1.0 | 1~10 | 1~10 | 0.2〜1.0 | 1~10 | 0.1~1.0 |
| 積分時間 \(T_{I}\) 秒 |
6~60 | 1000~1200 | 1000~1200 | 6~60 | 600~1200 (時定数\(T\) 次第) |
時定数\(T\) 次第 |
| 微分時間 \(T_{D}\) 秒 |
0 | 0 | 0 | 0 | 6〜60 | 0 |
制御を安定化させる微分制御ですが、化学プラントにおいては、ノイズやむだ時間のために使えないケースが多く、温度制御くらいにしか使用しません。
よって、むやみに微分制御を入れるのはやめましょう。(私も昔は、考えもなしに微分制御をいたる所で使っていました)
具体的なPIDパラメータの調整方法は下記の記事で解説しています。
-

-
化学系のためのPID制御パラメータの調整方法
続きを見る
その他のPIDパラメータの目安
その1
| 流量 制御 |
液面 制御 |
圧力 制御 |
温度 制御 |
組成 制御 |
|
| 比例帯 \(PB \%\) |
100〜500 | 10~100 | 10~50 | 50~200 | 50~200 |
| 比例ゲイン\(K_{p}\) | 0.2〜1 | 1~10 | 1~2 | 0.5~2 | 0.5~2 |
| 積分時間 \(T_{I}\) 秒 |
10~30 | 600~1800 | 60~600 | 200~1200 | 600〜3600 |
| 微分時間 \(T_{D}\) 秒 |
0 | 0 | 0 | (0.1〜0.25)\(T_{I}\) | (0.1〜0.25)\(T_{I}\) |
引用 矢野邦久:化学プラントにおける制御技術の現状と課題,計測と制御
その2
2020年の化学工学会誌に記載してあるデータであり、現時点で確認できる最新データだと思います。
| 流量 制御 |
液面 制御 |
圧力 制御 |
温度 制御 |
組成 制御 |
|
| 比例帯 \(PB \%\) |
100〜1000 | 10~100 | 10~200 | 50~200 | 50~200 |
| 比例ゲイン\(K_{p}\) | 0.1〜1 | 1~10 | 0.5~10 | 0.5~2 | 0.5~2 |
| 積分時間 \(T_{I}\) 秒 |
12~30 | 600~1800 | 60~600 | 180~1200 | 600〜3600 |
| 微分時間 \(T_{D}\) 秒 |
0 | 0 | 0 | (0.1〜0.25)\(T_{I}\) | (0.1〜0.25)\(T_{I}\) |
引用 化学工学_プロセス制御におけるPID制御-基礎と応用_第7回 PIDチューニング
参考文献
4.矢野邦久:化学プラントにおける制御技術の現状と課題,計測と制御 第52巻2013年5月号
5.化学工学_Vol.84_No.11_591_〔連載〕プロセス制御におけるPID制御-基礎と応用_第7回 PIDチューニング
はじめての制御工学は、初学者向けの本です。
制御工学の本は何冊か読みましたが、伝達関数、安定性、周波数応答、ナイキスト安定判別法の解説はこの本が一番わかりやすかったです。
この本の欠点は、化学プラントでは無視できない「むだ時間」の解説が無いことと、PID制御の説明が少ないこと(多く求めすぎか)です。
むだ時間の解説とPID制御の解説については、PID制御の基礎と応用で補うことができます。
1冊目の入門書としては使えないですが、非常に見やすく書かれており、PID制御について現場で見返したりする際にとても重宝しています。
PID制御 (システム制御情報ライブラリー)は、上級者向けの本です。PID制御について詳しく知りたくなったら読むべき教科書です。

