
ネットの無料計算ソフトでは、計算の中身がわからないし。
こんなお悩みを解決します。
どうも。こんにちは。
ケミカルエンジニアのこーしです。
本日は、配管圧力損失の計算方法について、わかりやすく解説していきます。
本記事の最後では、配管の圧力損失に影響を与えるパラメータについてグラフを作成し、考察しています。
他のサイトには見当たらない内容ですので、中級・上級者の方にも読んでいただければと思います。
本記事の内容
・配管圧力損失の計算式
・直管でない場合の圧力損失
・圧力損失の計算手順
・圧力損失の計算例
・圧力損失に影響を与えるパラメータ
この記事を書いた人

こーし(@mimikousi)
圧力損失とは

配管に流体(気体、液体)を流すためには、エネルギーが必要になります。
駆動力なしで走り続ける車がないのと同様に、配管を流れ続ける流体もありません。
これは、高校物理で習ったように摩擦力が働くためです。
流体は、進行方向と逆方向に働く摩擦力のために、エネルギーを失います。
これが、「圧力損失」の正体です。
流体のもつエネルギーは下記3つに分解して表すことができます。
流体のもつエネルギー = 運動エネルギー + 位置エネルギー + 圧力エネルギー
現実のプロセスでは、ほとんどの場合、配管入口ー出口間の配管径は等しく、流速は一定ですので、運動エネルギーは変化しません。
また、仮に配管入口ー出口で配管径が異なったとしても、運動エネルギーは他の2つのエネルギーと比較して、非常に小さいため無視して構いません。
つまり、流体のエネルギー変化を考える場合、「高さの差」と「圧力損失」の2点だけに着目すれば良いです。
また、単位質量あたりのエネルギー [J/kg]は、密度\(\rho\) [kg/m³]を掛けると圧力 [Pa]となり、重力加速度\(g\) [m/s²]で割るとヘッド [m]となるため、エネルギーは、圧力やヘッドの形で表現できることがわかります。
【エネルギーに密度\(\rho\) を掛けて、圧力に変換】
$$\begin{aligned}\frac {J}{kg}\times \frac {kg}{m^{3}}&=\frac {J}{m^{3}}\\[3pt]
&=\frac {N\cdot m}{m^{3}}\\[3pt]
&=\frac {N}{m^{2}}\\[3pt]
&=P_{a}\end{aligned}$$
【エネルギーを重力加速度\(g\)で割って、ヘッドに変換】
$$\begin{aligned}\frac {J}{kg}\div\frac {m}{s^{2}}&=\frac {N\cdot m}{kg}\times\frac {s^{2}}{m}\\[3pt]
&=\frac {kg\cdot m\cdot s^{-2}}{kg}\times s^{2}\\[3pt]
&=m\end{aligned}$$
【圧力を密度\(\rho\) と重力加速度\(g\)で割って、ヘッドに変換】
$$\begin{aligned}P_{a}\div \frac {kg}{m^{3}}\div \frac {m}{s^{2}}&=\frac {N}{m^{2}}\times \frac {m^{3}}{kg}\times \frac {s^{2}}{m}\\[3pt]
&=\frac {kg\cdot m\cdot s^{-2}\cdot s^{2}}{kg}\\[3pt]
&=m\end{aligned}$$
圧力 [Pa]を密度\(\rho\) [kg/m³]と重力加速度\(g\) [m/s²]で割って、ヘッド [m]に変換する方法はぜひ覚えておきましょう!
配管圧力損失の計算式
配管の圧力損失の計算式を下記に示します。
ファニング(fanning)の式
\(\Delta p\) : 圧力損失 [Pa]
\(f\) : 管摩擦係数 [-]
\(u\) : 流体の速度 [m/s]
\(\rho\): 流体の密度 [kg/m³] ※非圧縮性流体とする(例:水)
\(L\) : 配管長さ [m]
\(D\) : 配管内径 [m]
機械工学の教科書では、\(4f =\lambda\)とおいた下記の式が用いられますが、意味は同じです。
ダルシー・ワイスバッハ(Darcy-Weisbach)の式
\(\Delta p\) : 圧力損失 [Pa]
\(\lambda\) : 管摩擦係数 [-]
\(u\) : 流体の速度 [m/s]
\(\rho\): 流体の密度 [kg/m³] ※非圧縮性流体とする(例:水)
\(L\) : 配管長さ [m]
\(D\) : 配管内径 [m]
(1),(2)式を密度\(\rho\)と重力加速度\(g\)で割ると、ヘッド [m]の形に変換できます。
直管でない場合の圧力損失
(1)式や(2)式は、直管部分の圧力損失を計算しており、直管でない部分は下記のように圧力損失を計算します。
①タンクから配管への入口部
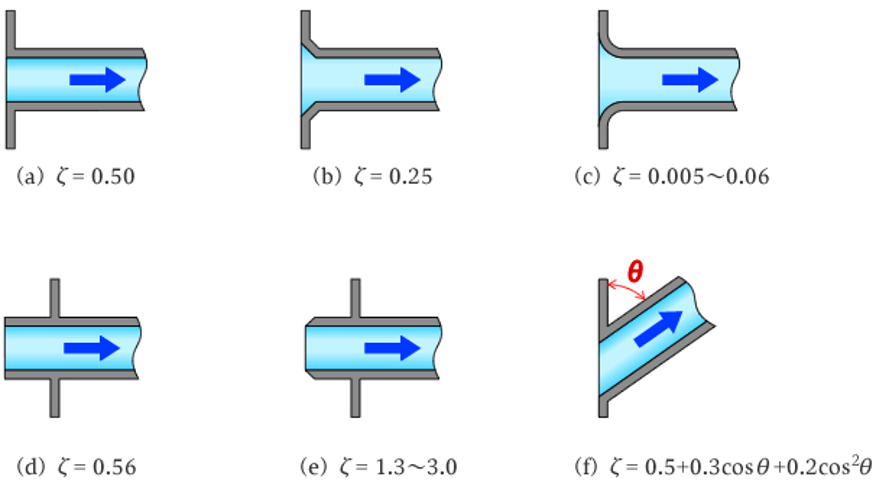
タンクから配管への入口部における圧力損失は、下記(3)式で表されます。
$$\Delta p=\zeta \frac {\rho u^{2}}{2}\tag{3}$$
上図のように、さまざまな配管パターンがあるため、該当する\(\zeta\)を読み取り圧力損失を算出します。
②急縮小
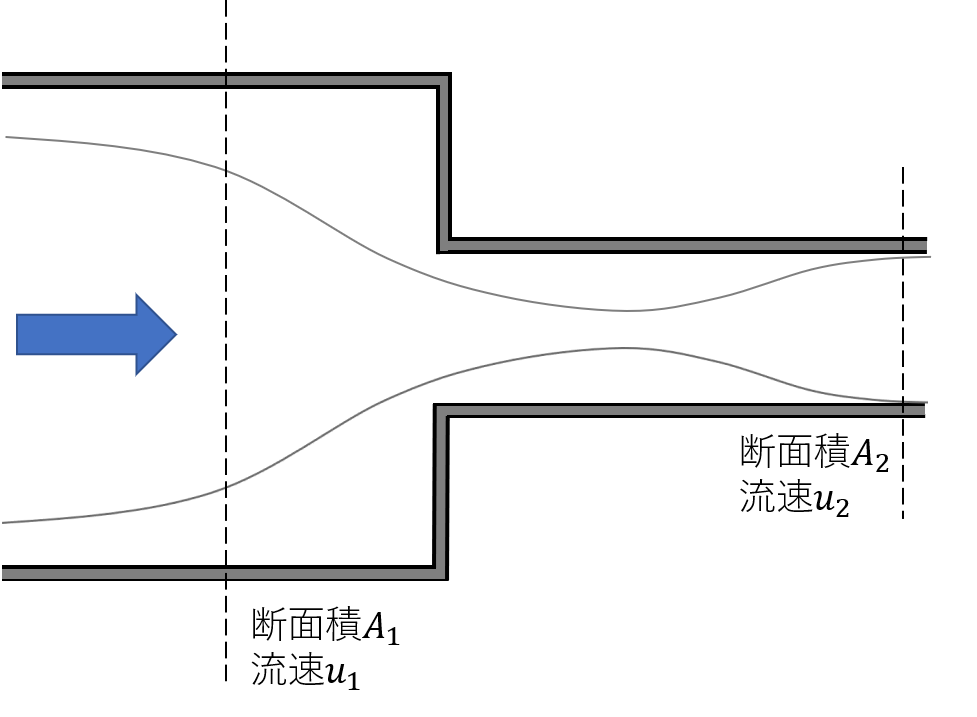
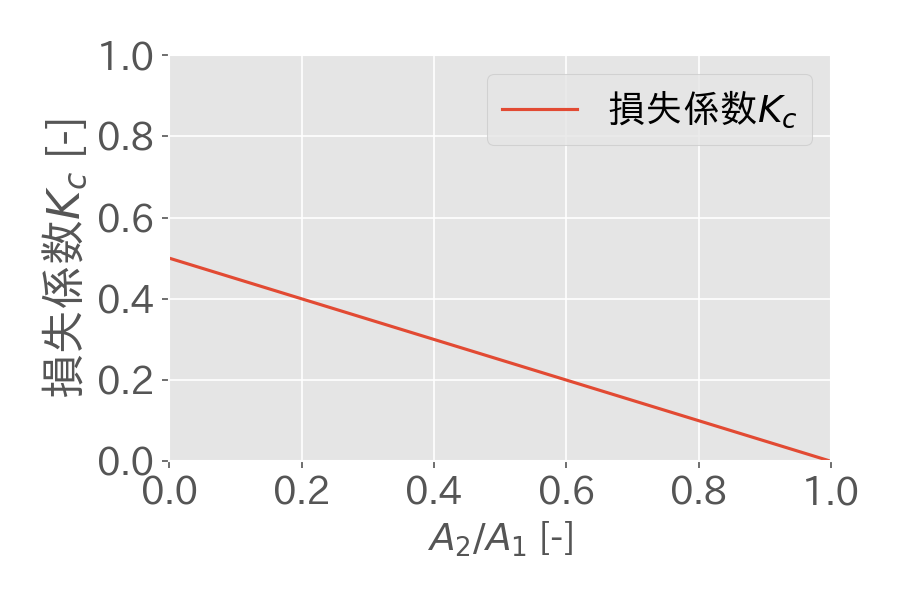
急縮小の圧力損失は、下記(4)式で算出します。
$$\Delta p=K_{c} \frac {\rho u_{2}^{2}}{2}\tag{4}$$
損失係数\(K_{c}\)は、急縮小前後の配管断面積の比\(A_{2}/A_{1}\)を算出し、上グラフから読み取ります。
急縮小も急拡大も、流速\(u\)は速い方(配管細い方)を計算に使用するので覚えておきましょう!
③急拡大
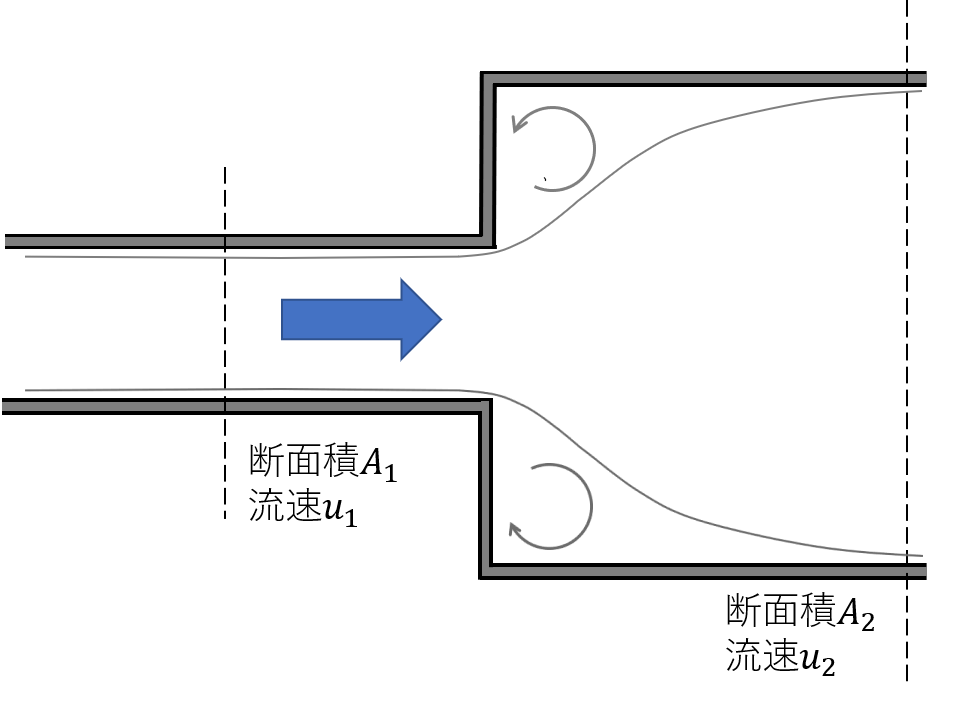
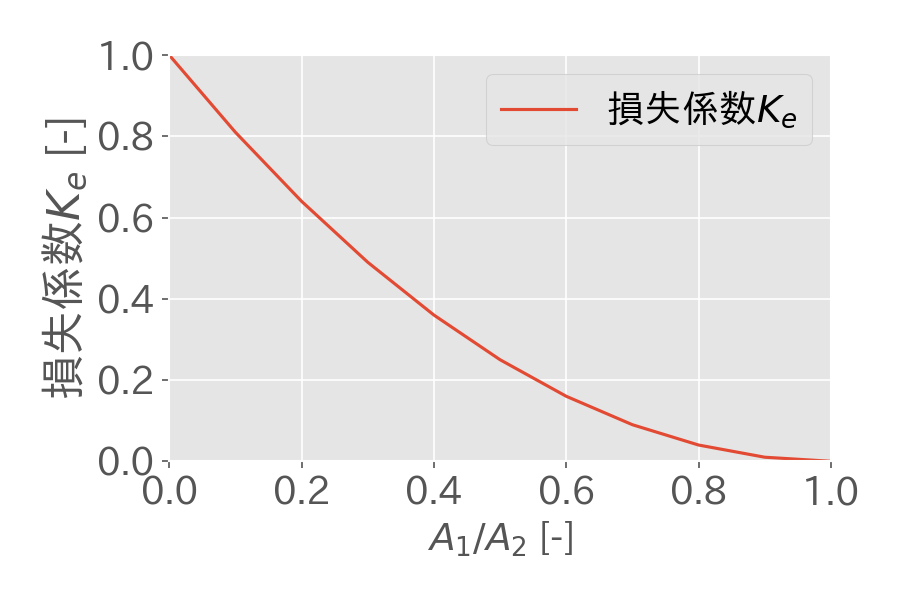
急拡大の圧力損失は、下記(5)式で算出します。
$$\Delta p=K_{e} \frac {\rho u_{1}^{2}}{2}\tag{5}$$
損失係数\(K_{e}\)は、急拡大前後の配管断面積の比\(A_{1}/A_{2}\)を算出し、上グラフから読み取ります。
④配管出口部
配管出口部は、急拡大の\(A_{2}\)が無限大に大きい場合に相当しますので、\(K_{e}=1\)となり、圧力損失は下記(6)式で求まります。
$$\Delta p=\frac {\rho u^{2}}{2}\tag{6}$$
⑤エルボやティー、バルブなど
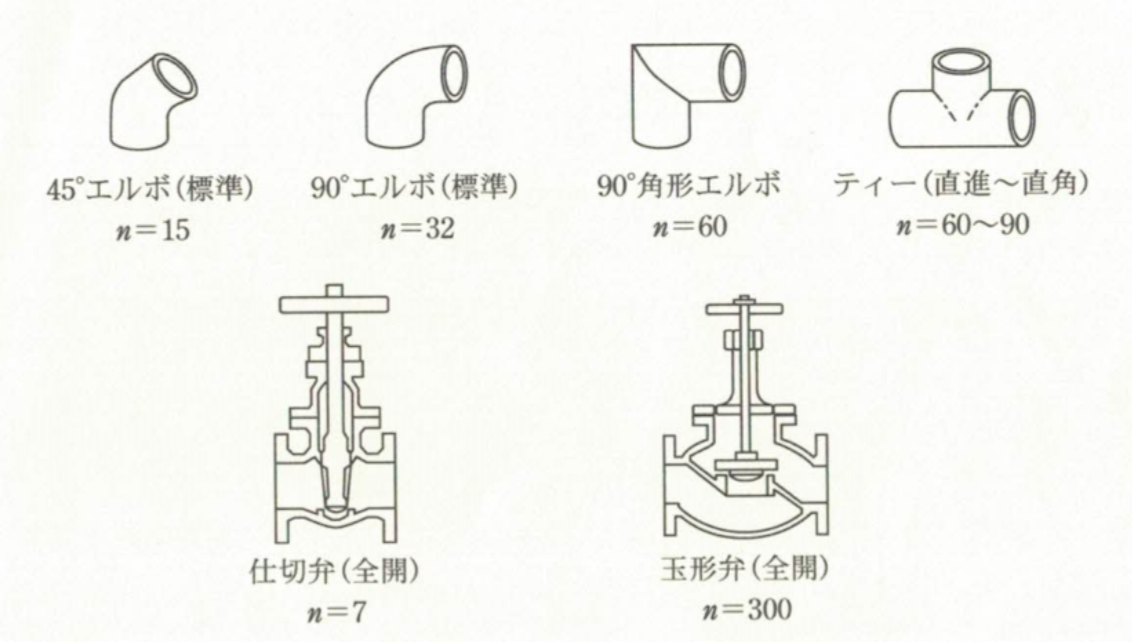
「化学工学 改定第3版 -解説と演習ー」より引用
エルボやティー、バルブの圧力損失の計算には、相当長さ\(Le\)を用います。
$$Le = nD\tag{7}$$
これは、エルボやティー、バルブの圧力損失が「直管何メートル分の圧力損失」に相当するかを表しています。
直管の長さを\(L'\)とすると、(1),(2)式の配管長さ\(L\)は下記(8)式のように表せます。
$$L=L'+Le\tag{8}$$
主なジョイントやバルブの相当長さ係数\(n\)を下表に示します。
| ジョイント、バルブ | 相当長さ係数\(n\) |
| 45°エルボ | 15 |
| 90°エルボ | 32 |
| 90°角形エルボ | 60 |
| 90°ベンド(曲率半径\(/D=3\)) | 24 |
| 90°ベンド(曲率半径\(/D=4\)) | 10 |
| 180°ベンド | 75 |
| ティー(直進~直角) | 60~90 |
| ユニオンカップリング | 0 |
| グローブ(玉形)弁(全開) | 300 |
| ゲート(仕切)弁(全開) | 7 |
| ゲート(仕切)弁(3/4開) | 40 |
| ゲート(仕切)弁(1/2開) | 200 |
| ゲート(仕切)弁(1/4開) | 800 |
| アングル弁(全開) | 170 |
| フート弁(全開) | 420 |
圧力損失の計算手順
それでは、圧力損失の計算手順を詳しく解説していきます。
(1)レイノルズ数\(Re\) [-]を求める
①流体の流速\(u\) [m/s]を求める。
配管の内径\(D\) [m]を用いて、配管の断面積\(A\) [m²]を求めると、下記(9)式となります。
$$A=\frac {\pi }{4}D^{2}\tag{9}$$
流量\(Q\) [m³/s]と配管の断面積\(A\) [m²]を用いると、流速\(u\) [m/s]は下記(10)式で求まります。
$$u=\frac {Q}{A}\tag{10}$$
②流体の密度\(\rho\) [kg/m³]を求める(気体の場合)
気体の場合、密度\(\rho\)は温度や圧力で大きく変動するため、温圧補正が必要になります。
気体のモル質量\(m\) [g/mol]、標準状態(大気圧101.3 kPa、0 ℃)のモル体積 0.0224 m³/mol、圧力\(P\) [kPaG]、温度\(T\) [℃]から、気体の密度\(\rho\)は下記(11)式で求まります。
液体の場合も密度は温度で若干は変化します。
取り扱う温度における密度を調べておきましょう!
③流体の粘度\(\mu\) [Pa・s]を調べる
流体の粘度\(\mu\)を化学便覧などで調べます.
粘度も温度に依存するので、取り扱う温度における粘度を調べます。
④レイノルズ数\(Re\)を計算する
レイノルズ数\(Re\)は下記(12)式で求まります。
$$Re=\frac {Du\rho}{\mu }\tag{12}$$
レイノルズ数\(Re\)は、流体の慣性力と粘性力の比を表す無次元数であり、\(Re\geq 4000\)では乱流、\(2300 <Re <4000\)では遷移域、\(Re\leq 2300\)では層流となります。
層流から乱流に変化する\(Re = 2300\)を臨界レイノルズ数といいます。
現実に取り扱う流体の多くは、レイノルズ数\(Re\)が大きく、乱流領域です。
詳しくは、こちらのサイトを参考にしてください。
層流、乱流、レイノルズ数とは?
(2)管摩擦係数\(f\) or \(\lambda\)を求める
①相対粗度\(\epsilon / D\) [-]を求める
下表のように配管の種類によって、粗滑度\(\epsilon\)と呼ばれる管壁表面の凹凸の高さが異なります。
該当する配管の粗滑度\(\epsilon\)を調べましょう。
| 配管の種類 | 粗滑度 \(\epsilon\) [m] |
| 引抜鋼管 | 0.000002~0.00001 |
| 市販鋼管 | 0.00005 |
| 鋳鉄管 | 0.00025~0.0005 |
| 亜鉛引管 | 0.00015 |
| コンクリート管 | 0.0003~0.003 |
②Moody線図から管摩擦係数\(f\) or\(\lambda\)を読み取る
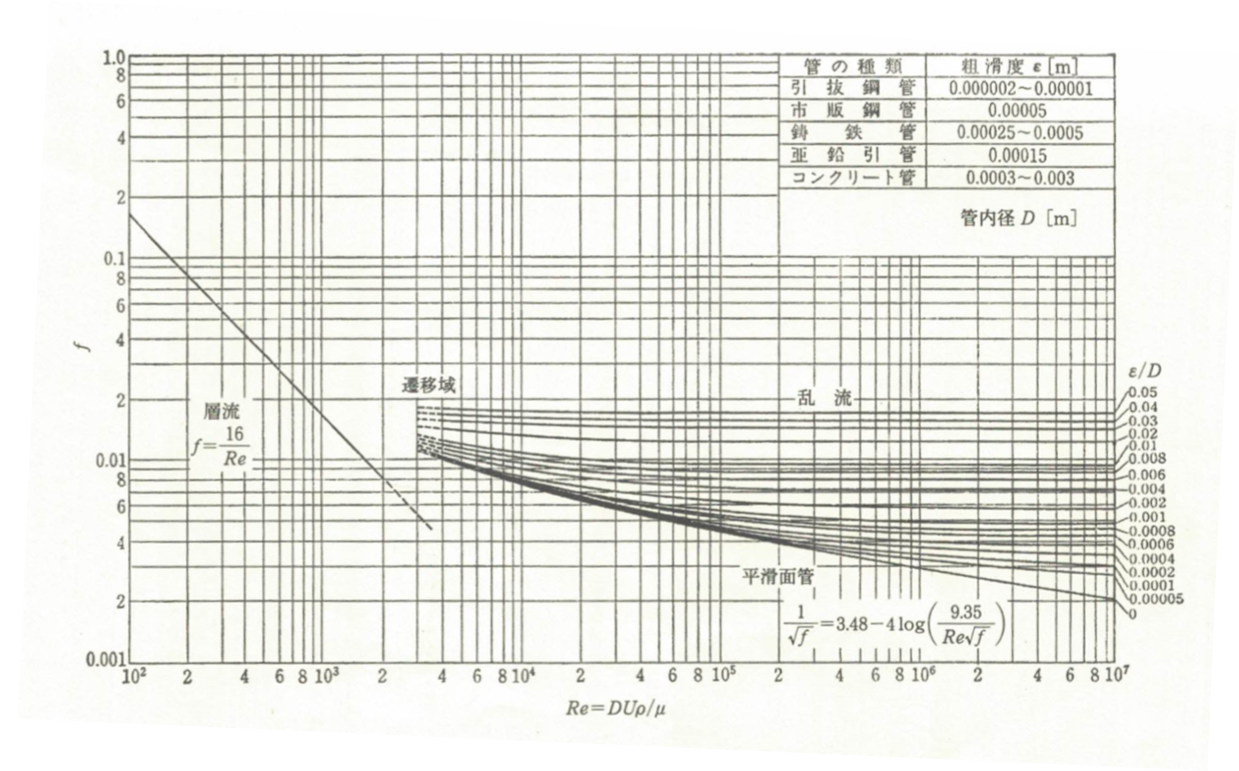
上図がMoody線図と呼ばれるグラフです。
レイノルズ数 \(Re\)と相対粗度\(\epsilon / D\)がわかれば、上図より管摩擦係数\(f\)を求めることができます。
(3)ファニングの式で圧力損失を計算する
①エルボやティー、バルブの相当長さ\(Le\)を算出し、直管長さ\(L'\)と足し合わせて、配管長さ\(L\)を求める。
$$L=L'+Le$$
②ファニングの式(1)式に、これまで求めた数値を代入し圧力損失を算出する。
$$\Delta p=4f\frac {\rho u^{2}}{2}\frac {L}{D}\tag{1}$$
③配管入口部、急縮小、急拡大、配管出口の圧力損失をそれぞれ算出する。
④ ②と③で求めた圧力損失を足し合わせる。
圧力損失の計算例

メモ
計算前提
ポンプ吐出流量 \(Q = 20\) m³/h(液体)
温度 \(T = 20\) ℃
密度 \(\rho = 1,000\) kg/m³
粘度 \(\mu = 0.001\) Pa・s
重力加速度 \(g =9.81\) m/s²
配管内径 \(D = 0.080\) m
配管の粗滑度 \(\epsilon = 0.00005\) m ※市販鋼管
上記のようなプロセス、前提条件にて、配管の圧力損失を計算していきましょう。
(1)レイノルズ数\(Re\) [-]を求める
①流体の流速\(u\) [m/s]を求める。
まず、配管の断面積\(A\)を配管内径\(D\)を用いて、下記のように求めます。
$$\begin{aligned}A&=\frac {\pi }{4}D^{2}\\[3pt]
&=\frac {\pi }{4}\times 0.080^{2}\\[3pt]
&=0.0050\ \textrm{m²}\end{aligned}$$
次に、流量\(Q\)を断面積\(A\)で割り、流速\(u\)を求めます。
$$\begin{aligned}u&=\frac {Q }{A}\\[3pt]
&=\frac {20/3600}{0.0050}\\[3pt]
&=1.1\ \textrm{m/s}\end{aligned}$$
②流体の密度\(\rho\) [kg/m³]を求める(気体の場合)
液体なので、取り扱い温度における密度を求めます。
今回は、計算前提の\(\rho = 1,000\) kg/m³を用います。
③流体の粘度\(\mu\) [Pa・s]を調べる
こちらも、取り扱い温度における粘度を求めます。
今回は、計算前提の\(\mu = 0.001\) Pa・sを用います。
④レイノルズ数\(Re\)を計算する
計算前提の配管内径\(D\)と①~③で求めたパラメータを(12)式に代入して、レイノルズ数\(Re\)を求めます。
$$\begin{aligned}Re&=\frac {Du\rho}{\mu }\\[3pt]
&=\frac {0.080\times 1.1\times 1000}{0.0010}\\[3pt]
&=8.8\times 10^{4}\end{aligned}$$
(2)管摩擦係数\(f\) or \(\lambda\)を求める
①相対粗度\(\epsilon / D\) [-]を求める
計算前提の配管内径\(D\)と粗滑度\(\epsilon\)を用いて、相対粗度\(\epsilon/D\)を求めます。
$$\frac {\varepsilon }{D}=\frac {0.00005}{0.080}=0.000625$$
②Moody線図から管摩擦係数\(f\) or\(\lambda\)を読み取る
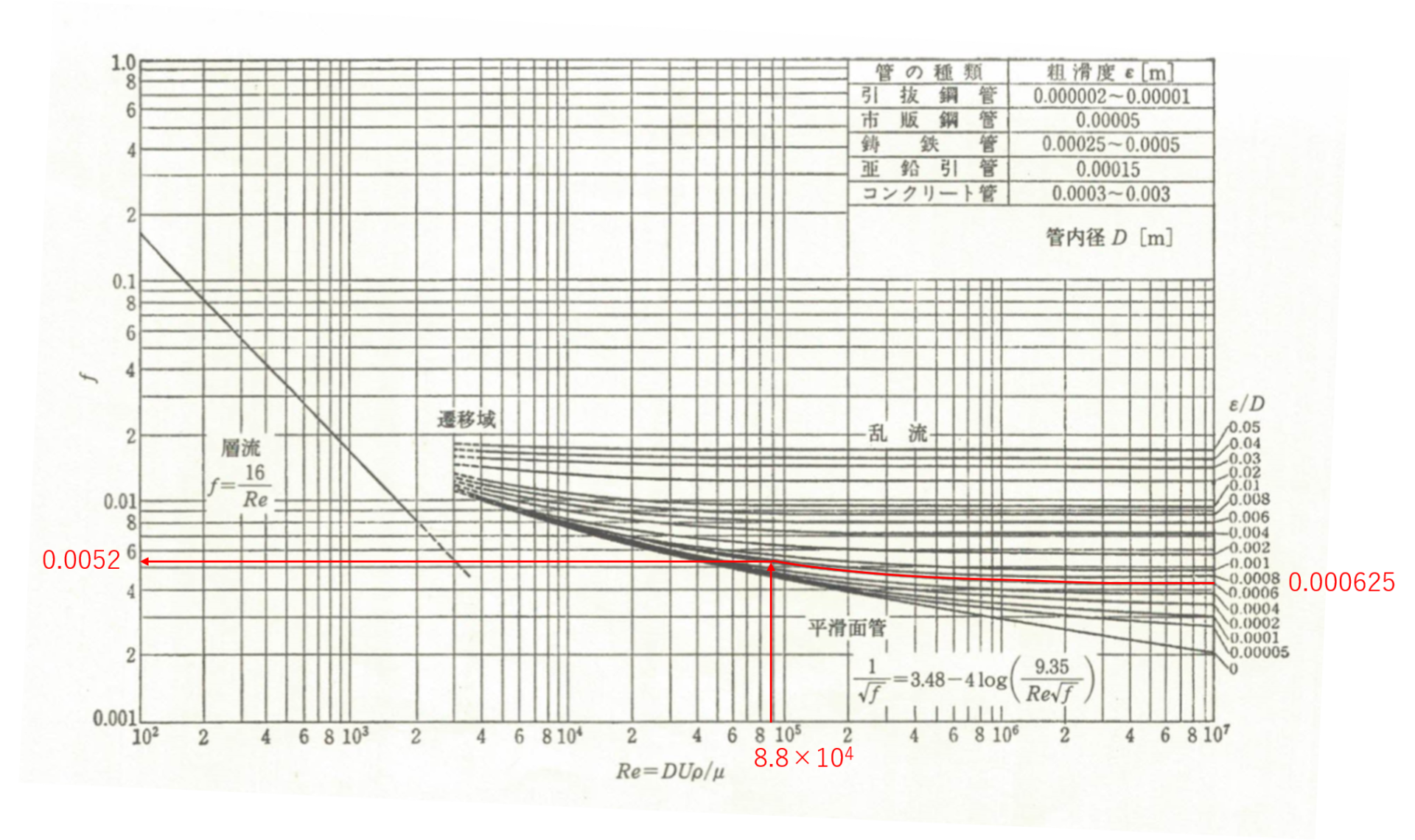
上図のように、求めたレイノルズ数\(Re=8.8\times 10^{4}\)と相対粗度\(\epsilon/D=0.000625\)より、管摩擦係数\(f\)が求まります。
$$f = 0.0052$$
(3)ファニングの式で圧力損失を計算する
①エルボやティー、バルブの相当長さ\(Le\)を算出し、直管長さ\(L'\)と足し合わせて、配管長さ\(L\)を求める。
計算前提のプロセス図から、直管長さと相当長さをそれぞれ下記の通り読み取ります。
- 直管長さ\(L'\)
&=29.5\ \textrm{m}\end{aligned}$$
- 90°エルボ(\(n=32\))が5個
$$Le_{1} = \left( 32\times 0.080\right) \times 5=12.8\ \textrm{m}$$
- ゲート弁(全開 \(n=7\))が1個
$$Le_{2} = 7\times 0.080=0.56\ \textrm{m}$$
- グローブ弁(全開 \(n=300\))が2個
$$Le_{3} = \left( 300\times 0.080\right) \times 2=48.0\ \textrm{m}$$
よって、
$$\begin{aligned}L&=L'+Le\\[3pt]
&=29.5+12.8+0.56+48.0\\[3pt]
&=90.9\ \textrm{m}\end{aligned}$$
②ファニングの式(1)式に、これまで求めた数値を代入し圧力損失を算出する。
ファニングの式で求めた圧力損失を\(\Delta p_{1}\)とおくと、
&=4\times 0.0052\times \frac {1000\times 1.1^{2}}{2}\times \frac {90.9}{0.0080}\\[3pt]
&=14299\ \textrm{Pa}\\[3pt]
&=14.3\ \textrm{kPa}\end{aligned}$$
③配管入口部、急縮小、急拡大、配管出口の圧力損失をそれぞれ算出する。
計算前提のプロセス図では、配管出口の圧力損失を計算する必要があります。
配管出口の圧力損失を\(\Delta p_{2}\)とおくと、
$$\begin{aligned}\Delta p_{2}&=\frac {\rho u^{2}}{2}\\[3pt]
&=\frac {1000\times 1.1^{2}}{2}\\[3pt]
&=605\ \textrm{Pa}\\[3pt]
&=0.61\ \textrm{kPa}\end{aligned}$$
④ ②と③で求めた圧力損失を足し合わせる。
したがって、配管の圧力損失\(\Delta p\)は、下記のように求めることができます。
$$\begin{aligned}\Delta p &= \Delta p_{1} + \Delta p_{2}\\[3pt]
&=14.3 + 0.61\\[3pt]
&=14.9\ \textrm{kPa}\end{aligned}$$
ここで、圧力損失\(\Delta p\)を圧力損失ヘッド\(\Delta P\)の形で表現してみます。
$$\begin{aligned}\Delta P &= \frac {\Delta p}{\rho g}\\[3pt]
&=\frac {14.9\times 1000}{1000\times 9.81}\\[3pt]
&=1.5\ \textrm{m}\end{aligned}$$
よって、配管の圧力損失は、液体を\(1.5\) m分持ち上げるのに必要なエネルギーに相当するということがわかりました。
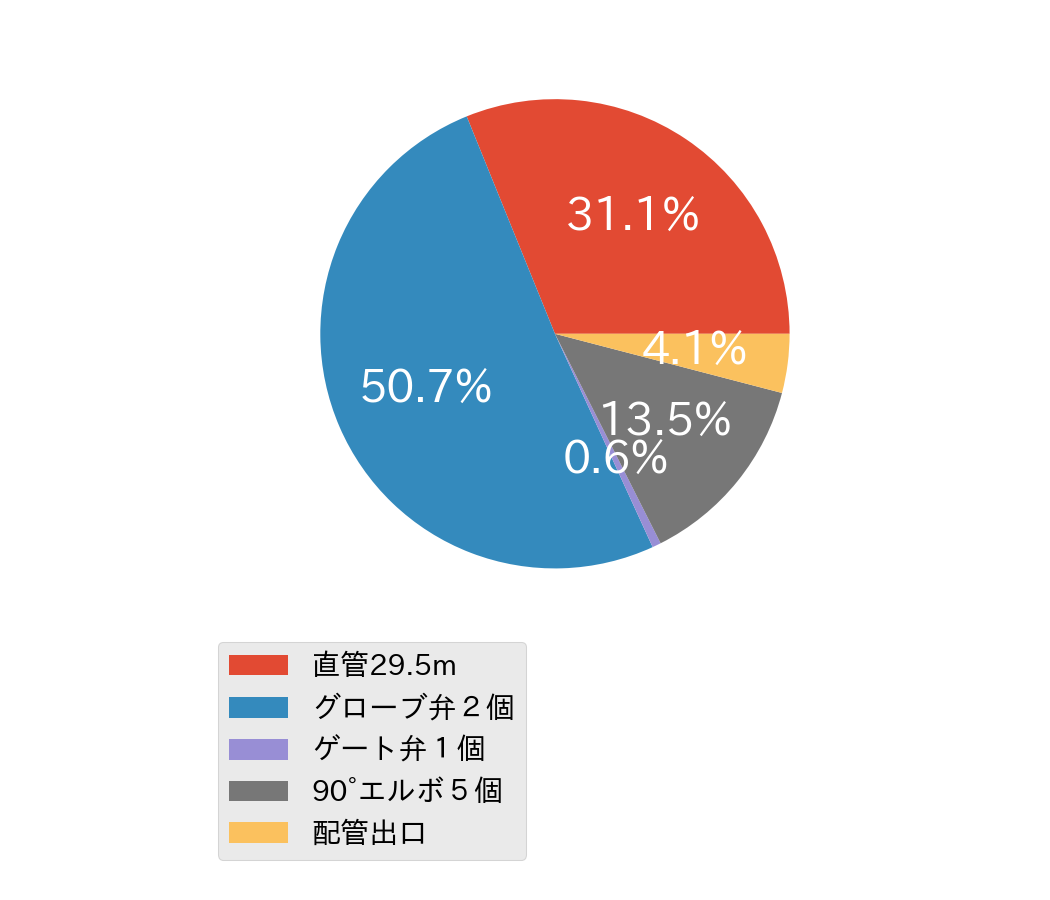
また、各圧力損失の割合を円グラフで表してみました。
上図より、グローブ弁の圧力損失が大半を占めていることがわかります。
一方で、ゲート弁の圧力損失は非常に低く、プロセスの圧力損失を下げたい場合は、グローブ弁からゲート弁への変更が効果的だとわかります。
圧力損失に影響を与えるパラメータ
各パラメータを変更した際に、圧力損失がどのように変化するのかを調べ、グラフにしてみました。
圧力損失\(\Delta p\) [kPa]だけでなく、ヘッドに変換した配管損失ヘッド [m]も算出しています。
流速\(u\) [m/s]
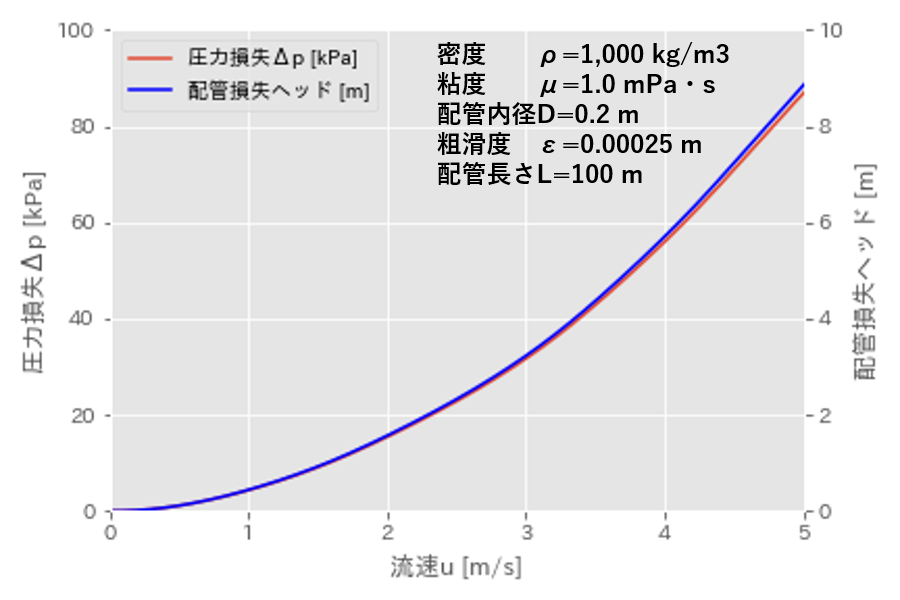
(1)式や上図からもわかるように、圧力損失\(\Delta p\) は流速\(u\)の2乗に比例します。
流速が大きいと、圧力損失が非常に大きくなってしまいますので、配管の標準流速は、1~3 m/s程度と言われています。
配管長さ\(L\) [m]
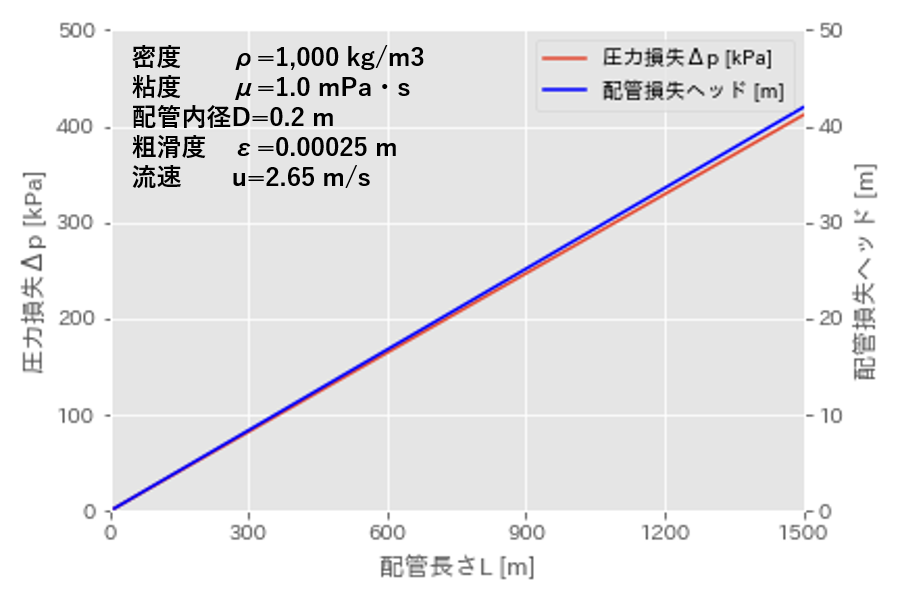
(1)式や上図からもわかるように、圧力損失\(\Delta p\) は配管長さ\(L\)に比例します。
配管内径\(D\) [m]
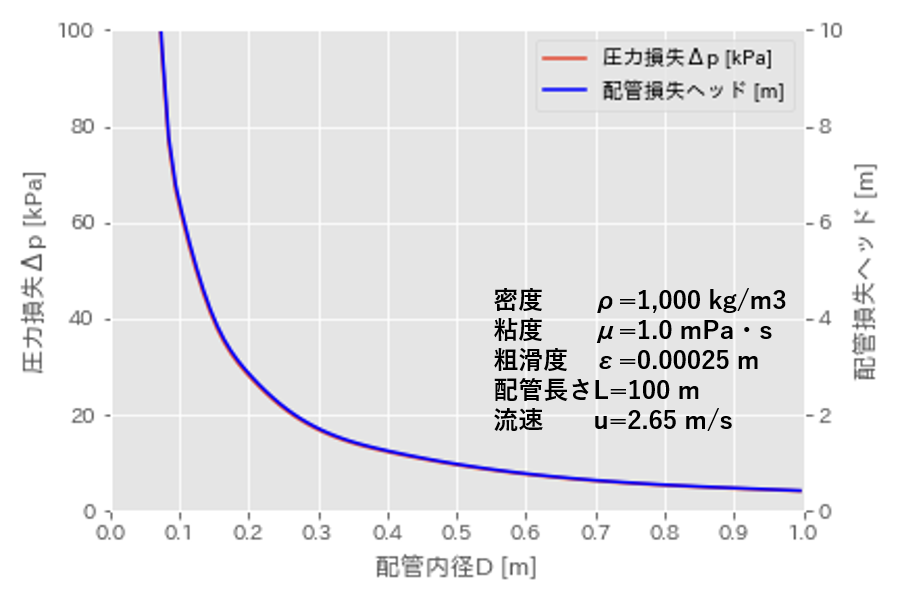
(1)式や上図からもわかるように、流速\(u\)一定の条件では、圧力損失\(\Delta p\) は配管内径\(D\)に反比例します。
また、配管内径\(D\)が小さい条件だと、相対粗度\(\epsilon/D\)が大きくなってしまい、管摩擦係数\(f\)も大きくなります。
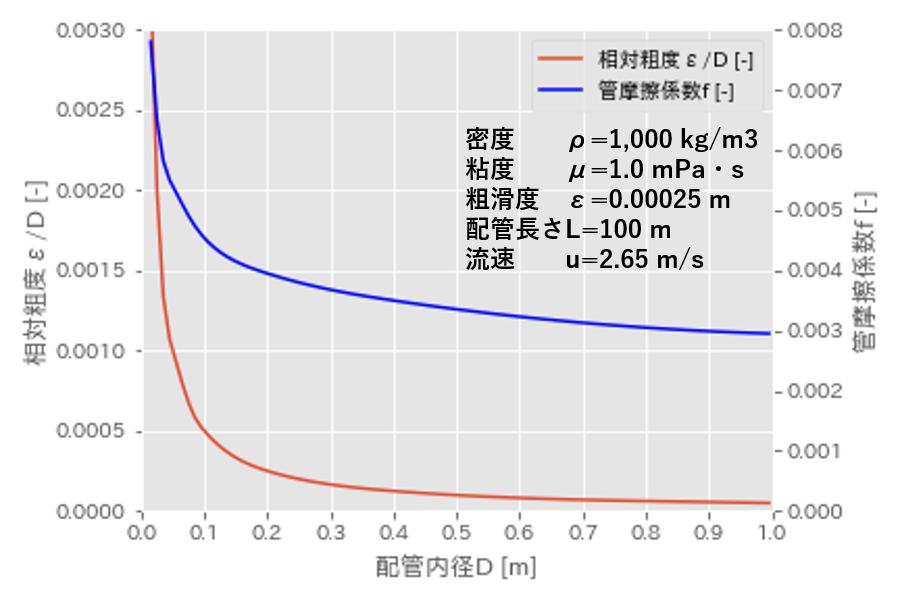
流速\(u\)一定条件で、配管内径\(D\)を変化させた際の相対粗度\(\epsilon/D\)と管摩擦係数\(f\)の変化を上図に示しました。
配管が細い場合は、相対粗度\(\epsilon/D\)が大きくなってしまうため、極力、粗滑度\(\epsilon\)の小さい滑らかな配管を使用する必要があります。
粗滑度\(\epsilon\) [m]
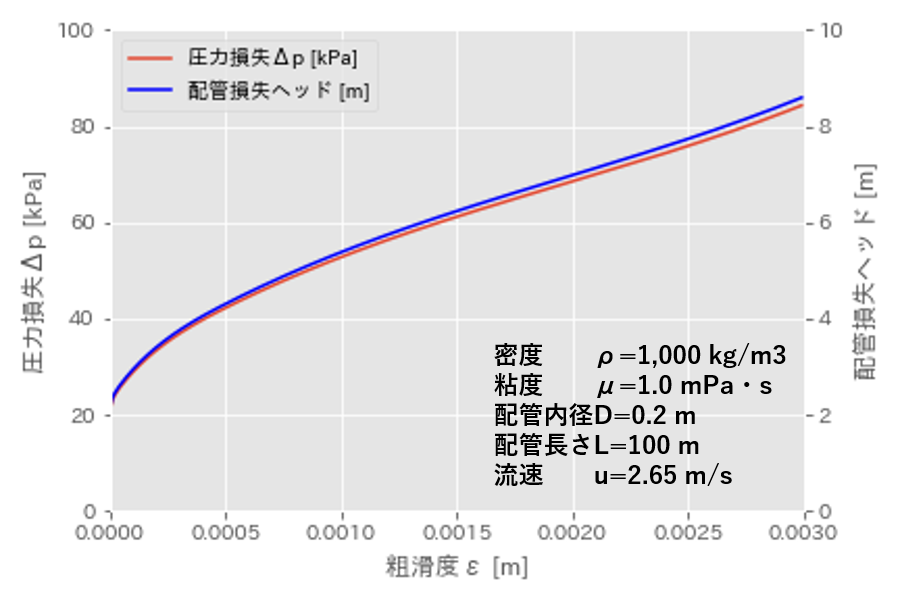
粗滑度\(\epsilon\)が大きくなると、管摩擦係数\(f\)が大きくなり、圧力損失\(\Delta p\) が増加します。
密度\(\rho\) [kg/m³]
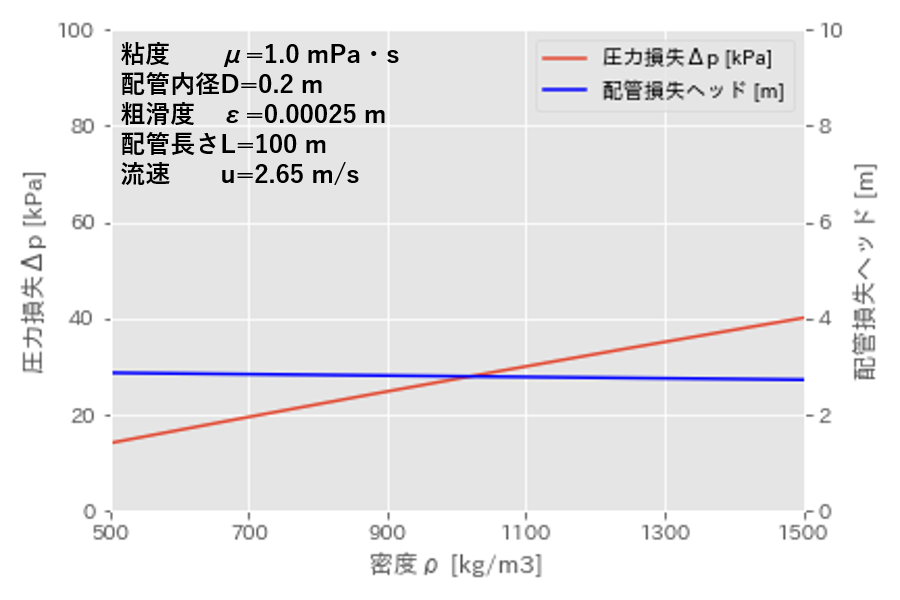
続いて、物性値である密度\(\rho\)を変化させた場合を見ていきます。
(1)式や上図からもわかるように、密度\(\rho\)が大きくなると圧力損失\(\Delta p\) も増加します。
しかし配管損失ヘッドは、ほぼ一定となり、密度\(\rho\)に依存しないことがわかります。
密度\(\rho\)が大きいと、圧力損失\(\Delta p\)も大きくなりますが、もともと持っていた運動エネルギーや位置エネルギーも大きくなるため、相殺されます。
よって、 損失エネルギーは、密度\(\rho\)にほとんど依存しないということがわかります。
粘度\(\mu\) [Pa・s]
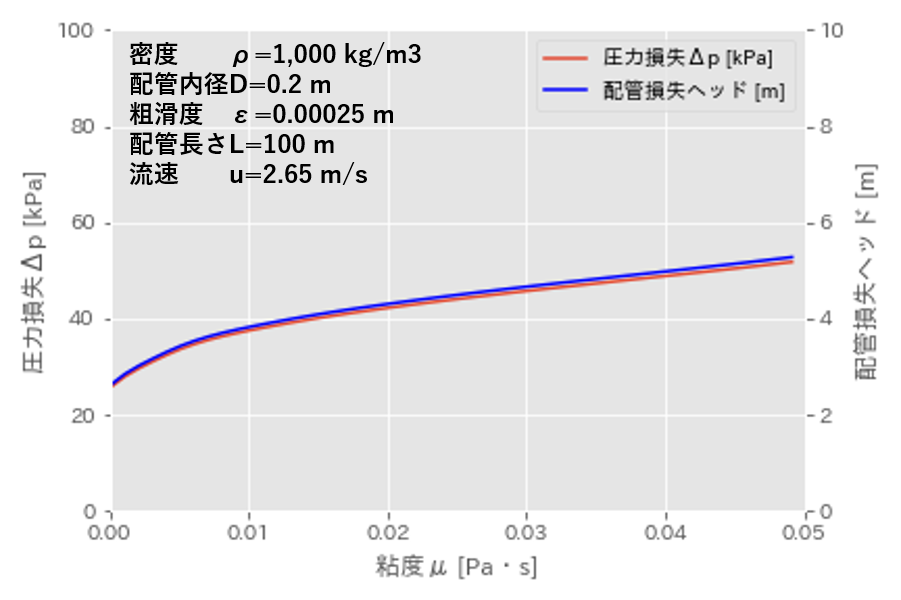
粘度\(\mu\)が大きくなると、レイノルズ数\(Re\)が小さくなり、管摩擦係数\(f\)が大きくなります。
よって、上図のように粘度\(\mu\)が大きくなると圧力損失\(\Delta p\) が増加します。
注意ポイント
①流速\(u\)が適正値(\(1\sim3\) m/s)か
②粗滑度\(\epsilon\)が大きすぎないか
この2点だけは確認しておきましょう!
まとめ
ポイント
- 配管の圧力損失とは、摩擦抵抗によるエネルギーロスのこと
- 圧力損失は、ファニングの式(ダルシーワイスバッハの式)で求めることができる
$$\large{\Delta p=4f\frac {\rho u^{2}}{2}\frac {L}{D}}$$
- 直管よりもグローブ弁の圧力損失の方が大きい
- 弁(バルブ)の種類によって圧力損失が大きく異なる
参考文献
1.はじめての化学工学 プロセスから学ぶ基礎 化学工学会高等教育委員会 (編集) P.102~105
