誰かわかりやすく解説してくれないかな？
こんなお悩みを解決します。
どうも。こんにちは。
ケミカルエンジニアのこーしです。
本日は、「総括伝熱係数（Ｕ値）とは？」についてわかりやすく解説していきます。
化学プラントにおいて、熱交換器の総括伝熱係数（Ｕ値）は避けて通れない指標です。
本記事では、オームの法則のアナロジー（類推）を使って解説しますので、実務で使えるレベルまで理解が進むと思います。
大事な内容なので、しっかり勉強していきましょう！
本記事の内容
・総括伝熱係数（Ｕ値）とは
・オームの法則のアナロジー（類推）
・熱交換器の伝熱速度式\(Q=UA\Delta T_{lm}\)
・対数平均温度差\(\Delta T_{lm}\)とは
この記事を書いた人
こーし(@mimikousi)
目次
総括伝熱係数（Ｕ値）とは？
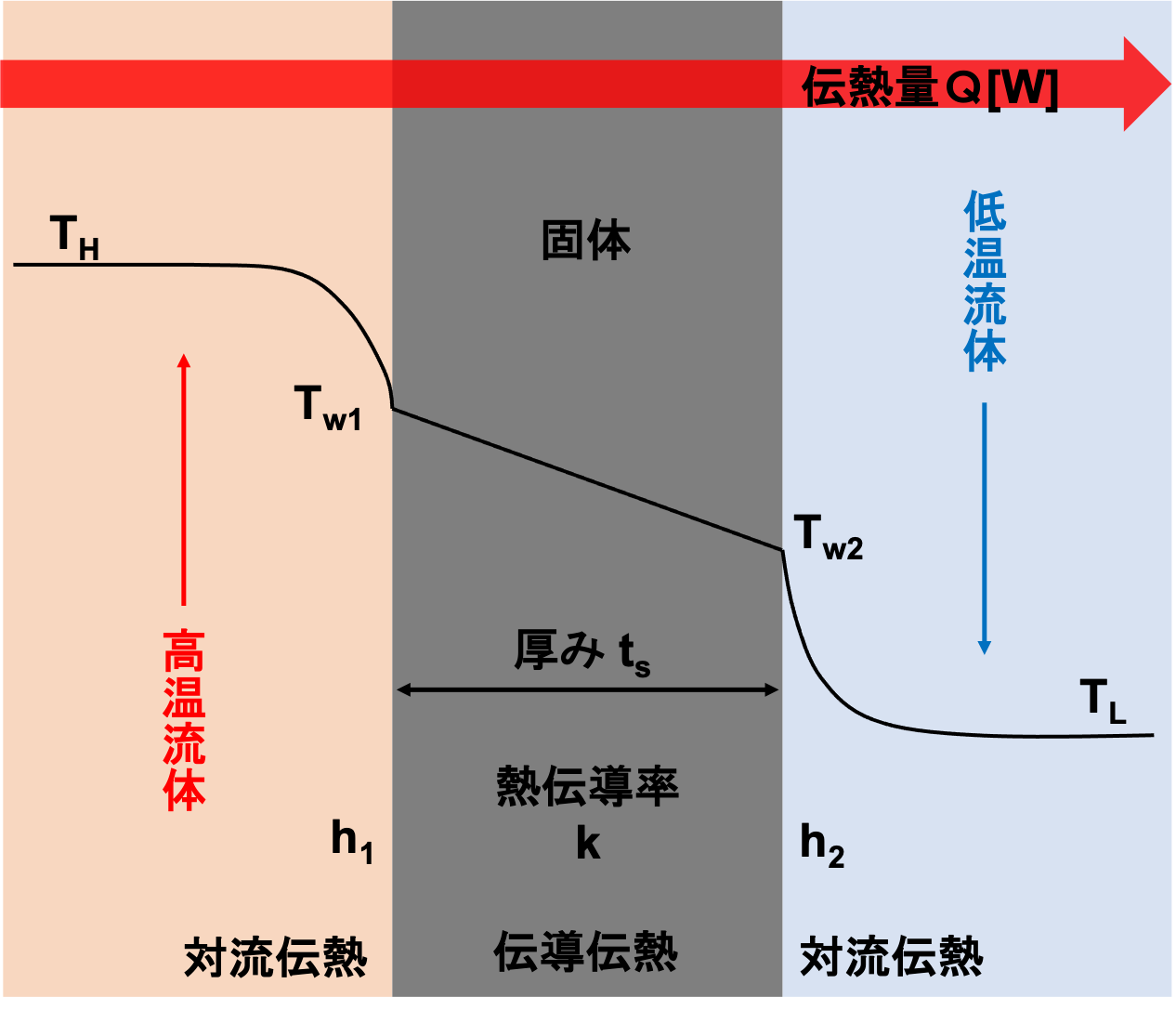
記号の説明
伝熱量 \(Q\) [W]
高温流体の温度 \(T_H\) [K]
低温流体の温度 \(T_L\) [K]
高温側固体表面温度 \(T_{w1}\) [K]
低温側固体表面温度 \(T_{w2}\) [K]
高温流体の境膜伝熱係数 \(h_1\) [W/(m2・K)]
低温流体の境膜伝熱係数 \(h_2\) [W/(m2・K)]
固体の熱伝導率 \(k\) [W/(m・K)]
固体の厚さ \(t_s\) [m]
上図のように、伝熱装置（熱交換器など）において、3つの熱移動が直列的に生じている場合を考えます。
3つの熱移動
- 高温流体ー固体壁表面間の対流伝熱
- 固体壁内の伝導伝熱
- 固体壁表面ー低温流体間の対流伝熱
このとき、伝熱量\(Q\)は、下式のように書けます。
伝熱量の式
$$Q=UA(T_H-T_L)\tag{1}$$
記号の説明
伝熱量 \(Q\) [W]
総括伝熱係数 \(U\) [W/(m2・K)]
伝熱面積 \(A\) [m2]
高温流体の温度 \(T_H\) [K]
低温流体の温度 \(T_L\) [K]
よって、上式の係数\(U\)を総括伝熱係数（英語：over-all heat transfer coefficient）と呼び、3つの熱移動を総括した伝熱係数となります。
ちなみに、対流伝熱と伝導伝熱について簡単に説明すると、下記の通りです。
対流伝熱：流体と固体表面との間で行われる熱移動
伝導伝熱：固体内の分子・電子の微視的な運動によって熱が伝わる現象
また、流体の移動が、温度差による密度差に起因する場合を自然対流といい、ポンプやブロワなどの強制的な外力に起因する場合を強制対流と言います。
総括伝熱係数（Ｕ値）の構成（中身）
それでは、総括伝熱係数（U値）の構成（中身）を具体的に見ていきましょう！
3つの熱移動の伝熱量\(Q\)は等しいので、下式のように書けます。
$$\begin{aligned}Q&=h_1A(T_H-T_{w1})\\[3pt]
&=\frac {kA}{t_s}(T_{w1}-T_{w2})\\[3pt]
&=h_2A(T_{w2}-T_L)\end{aligned}\tag{2}$$
左辺に温度差をもってくると、(2)式は(3)式のように変形できます。
$$\begin{aligned}T_H-T_{w1}&=\frac{1}{h_1A}Q\\[3pt]
T_{w1}-T_{w2}&=\frac {t_s}{kA}Q\\[3pt]
T_{w2}-T_L&=\frac{1}{h_2A}Q\end{aligned}\tag{3}$$
ここで、(3)式をそれぞれ足し合わせると、左辺から\(T_{w1}\),\(T_{w2}\)が消え、
$$T_H-T_L=\left(\frac{1}{h_1A}+\frac{t_s}{kA}+\frac{1}{h_2A} \right)Q$$
伝熱量\(Q\)の式に変形すると、下記(4)式が得られます。
$$Q=\frac {1}{\frac{1}{h_1A}+\frac{t_s}{kA}+\frac{1}{h_2A}}(T_H-T_L)\tag{4}$$
(4)式の分母は、総括伝熱抵抗\(\left(\dfrac{1}{UA}\right)\)と呼ばれ、3つの伝熱抵抗の直列結合（足し算）になっています。
$$\begin{aligned}\frac{1}{h_1A}+\frac{t_s}{kA}+\frac{1}{h_2A}&=\left(\frac{1}{h_1}+\frac{t_s}{k}+\frac{1}{h_2} \right)\frac{1}{A}\\[3pt]
&=\frac{1}{UA}\end{aligned}\tag{5}$$
3つの熱移動の伝熱抵抗
- 伝導伝熱抵抗：\(\dfrac{t_s}{kA}\)
- 対流（境膜）伝熱抵抗：\(\dfrac{1}{h_1A}, \dfrac{1}{h_2A}\)
(5)式を(4)式に代入すると、下式のように整理できます。
$$\begin{aligned}Q&=\frac{1}{\frac{1}{UA}}(T_H-T_L)\\[3pt]
Q&=UA(T_H-T_L)\end{aligned}\tag{6}$$
(6)式は、最初に示した(1)式と一致することがわかります。
よって、3つの熱移動の伝熱量\(Q\)の式を求め、各伝熱係数の逆数（伝熱抵抗）を足し算することで、総括伝熱係数\(U\)を算出することができます。
ちなみに、総括伝熱係数の逆数\(\dfrac{1}{U}\)は、(5)式からわかるように下式のように書くことができます。
$$\frac{1}{U}=\frac{1}{h_1}+\frac{t_s}{k}+\frac{1}{h_2}\tag{7}$$
これが総括伝熱係数(U値)の正体です。
ここで、総括伝熱係数(U値)は、伝熱抵抗が最大になるものの影響を強く受けます。
よって、どの熱移動の伝熱抵抗が最大（律速）なのかを把握することが、熱交換器の設計や運転管理で重要になります。
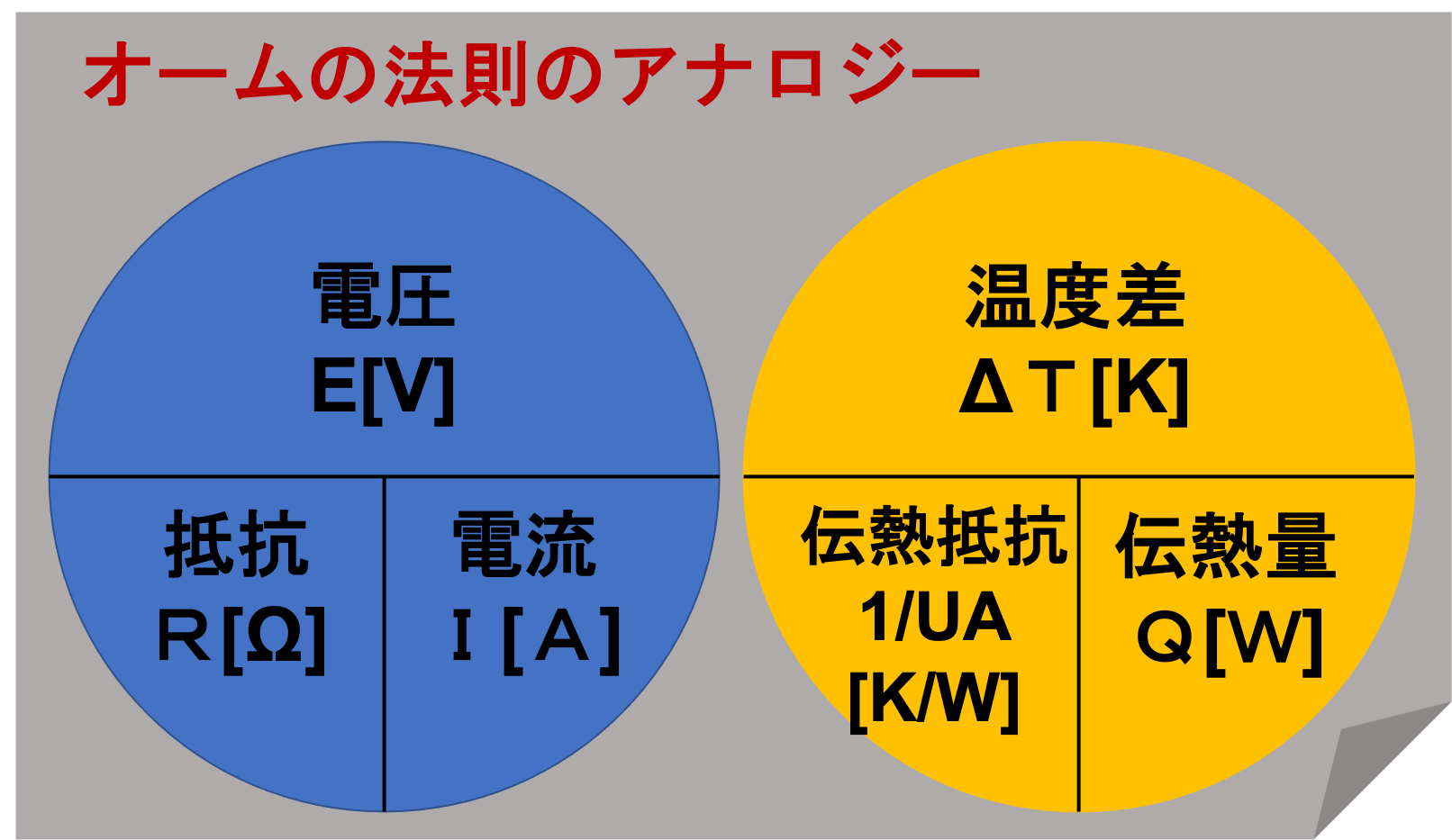
オームの法則のアナロジー（類推）
総括伝熱係数(U値)について、もう少しわかりやすく解説してみます。
伝熱は、オームの法則のアナロジー（類推）として考えることができます。
オームの法則
$$E(V) = R(\Omega) \times I(A)\tag{8}$$
記号の説明
電圧：\(E\) [V]
抵抗：\(R\) [Ω]
電流：\(I\) [A]
よって、伝熱量\(Q\)の式をオームの法則に対応させると、
- 電圧\(E\) ＝ 温度差（\(\Delta T=T_H-T_L\)）
- 抵抗\(R\) ＝ 伝熱抵抗\(\dfrac{1}{UA}\)
- 電流\(I\) ＝ 伝熱量\(Q\)
となるので、伝熱量\(Q\)の式である(1)式は、オームの法則と同じ形にすると、下記(9)式のように変形できます。
伝熱量の式（オームの法則）
$$Q=UA(T_H-T_L)\tag{1}$$
$$\Delta T= \frac{1}{UA}\times Q\tag{9}$$
よって、推進力を表している温度差\(\Delta T\)が大きいほど、伝熱量\(Q\)は大きくなります。
一方、伝熱抵抗\(\dfrac{1}{UA}\)が大きいほど、伝熱量\(Q\)は小さくなります。
【参考記事】
熱交換器の伝熱速度式\(Q=U_oA_o\Delta T_{lm}\)
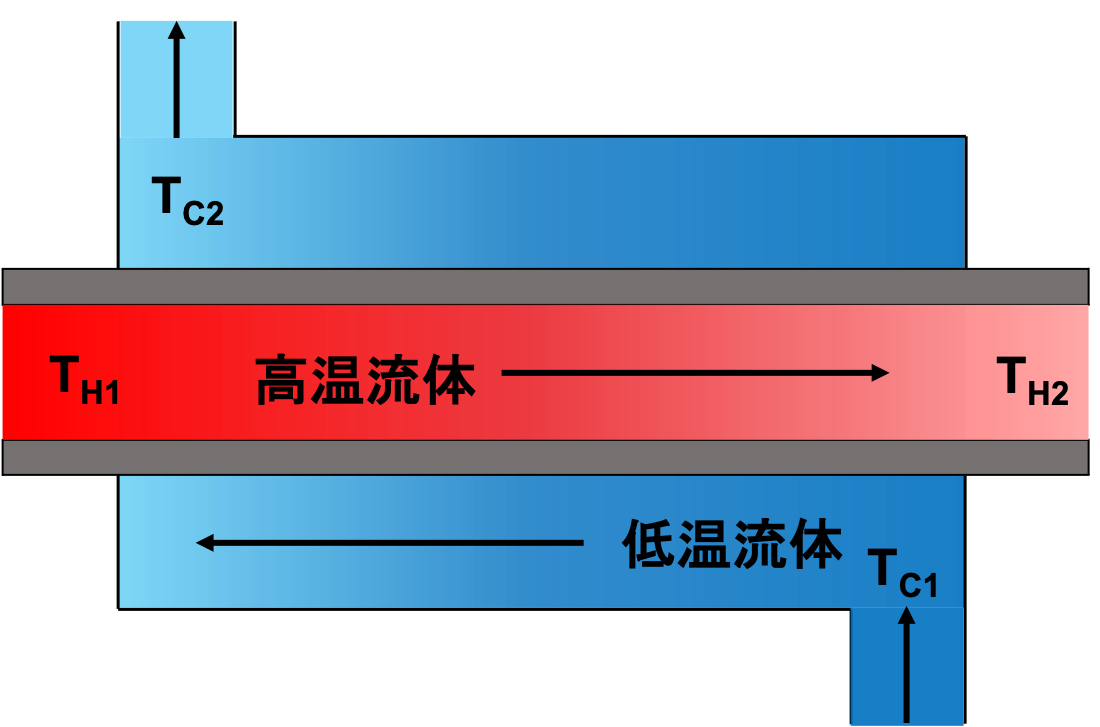
上図は、一般的な熱交換器の概略図です。
二重管式熱交換器とも呼ばれており、多数の管（チューブ）を用いた「多管式熱交換器（シェル＆チューブ熱交換器）」が最も広く使用されています。
ここで、熱交換器の伝熱速度式を下記に示します。
熱交換器の伝熱速度式
$$Q = U_oA_o\Delta T_{lm}\tag{10}$$
記号の説明
伝熱量 \(Q\) [W]
（外面基準）総括伝熱係数 \(U_o\) [W/(m2・K)]
（外面基準）伝熱面積 \(A_o\) [m2]
対数平均温度差\(\Delta T_{lm}\)
これまで解説してきた伝熱量\(Q\)の式と上の熱交換器の伝熱速度式で異なる点は、下記の通りです。
- 総括伝熱係数\(U_o\)の構成（中身）が異なる。
⇒熱交換器では、汚れ係数を考慮する必要がある。 - 基準伝熱面積（\(A_o\)）を考える。
⇒管の外面と内面で伝熱面積が異なるため。 - 温度差\(\Delta T = T_H - T_L\)が対数平均温度差\(\Delta T_{lm}\)になっている。
⇒熱交換器内の温度変化を考慮するため。
それでは、一つずつ詳しく解説していきます。
熱交換器の総括伝熱係数\(U_o\)（外面基準）
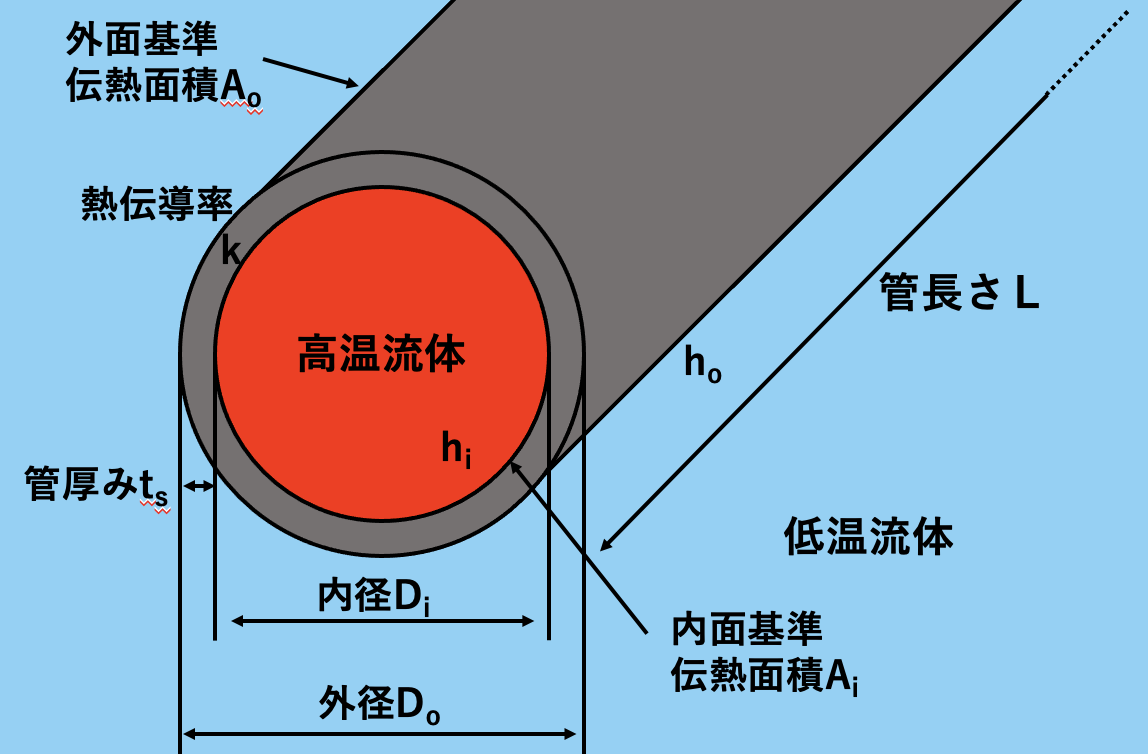
記号の説明
高温流体の境膜伝熱係数 \(h_i\) [W/(m2・K)]
低温流体の境膜伝熱係数 \(h_o\) [W/(m2・K)]
管の熱伝導率 \(k\) [W/(m・K)]
管厚み \(t_s\) [m]
管長さ \(L\) [m]
内径 \(D_i\) [m]
外径 \(D_o\) [m]
内面基準伝熱面積 \(A_i\) [m2]
外面基準伝熱面積\(A_o\) [m2]
それでは、上図を参考に熱交換器の伝熱抵抗\(\dfrac{1}{U_oA_o}\)を求めてみます。
管の外面と内面で伝熱面積が異なるため、今回は外面基準の伝熱面積\(A_o\)を用います。
また、現実の熱交換器では管壁に汚れ（スケール）が溜まり、伝熱抵抗となりますので、汚れ係数\(\gamma_i,\gamma_o\)[m2・K/W]を伝熱抵抗として導入し、直列結合します。
よって、伝熱抵抗\(\dfrac{1}{U_oA_o}\)は下式のように書けます。
$$\frac{1}{U_oA_o} = \frac{1}{h_oA_o} +\frac{\gamma_o}{A_o}+\frac{t_s}{kA_m}+\frac{\gamma_i}{A_i}+\frac{1}{h_iA_i}\tag{11}$$
上式における管の平均伝熱面積\(A_m\)は、管平均径\(D_m\)を使って下記のように表されます。
$$A_m =\pi D_mL$$
$$D_m = \frac{D_o -D_i}{\ln \left(\frac{D_o}{D_i}\right)}$$
ここで、(11)式の両辺に外面基準の伝熱面積\(A_o\)を掛けると、(12)式が得られます。
$$\frac{1}{U_o} = \frac{1}{h_o} +\gamma_o+\frac{t_s}{k}\left(\frac{A_o}{A_m}\right)+\gamma_i\left(\frac{A_o}{A_i}\right)+\frac{1}{h_i}\left(\frac{A_o}{A_i}\right)\tag{12}$$
そして、計算しやすくするため、伝熱面積を下記のように管の内径、外径に変形します。
$$\begin{aligned}\frac{A_o}{A_m} &= \frac{\pi D_o L}{\pi D_m L}\\[3pt]
&=\frac{D_o}{D_m}\end{aligned}$$
$$\begin{aligned}\frac{A_o}{A_i} &= \frac{\pi D_o L}{\pi D_i L}\\[3pt]
&=\frac{D_o}{D_i}\end{aligned}$$
よって、(13)、(14)式が得られます。
熱交換器の総括伝熱係数
$$\frac{1}{U_o} = \frac{1}{h_o} +\gamma_o+\frac{t_s}{k}\left(\frac{D_o}{D_m}\right)+\gamma_i\left(\frac{D_o}{D_i}\right)+\frac{1}{h_i}\left(\frac{D_o}{D_i}\right)\tag{13}$$
$$U_o = \frac{1}{\frac{1}{h_o} +\gamma_o+\frac{t_s}{k}\left(\frac{D_o}{D_m}\right)+\gamma_i\left(\frac{D_o}{D_i}\right)+\frac{1}{h_i}\left(\frac{D_o}{D_i}\right)}\tag{14}$$
最後に、対数平均温度差\(\Delta T_{lm}\)について解説するよ！
あと一息頑張ろう！！
対数平均温度差\(\Delta T_{lm}\)とは
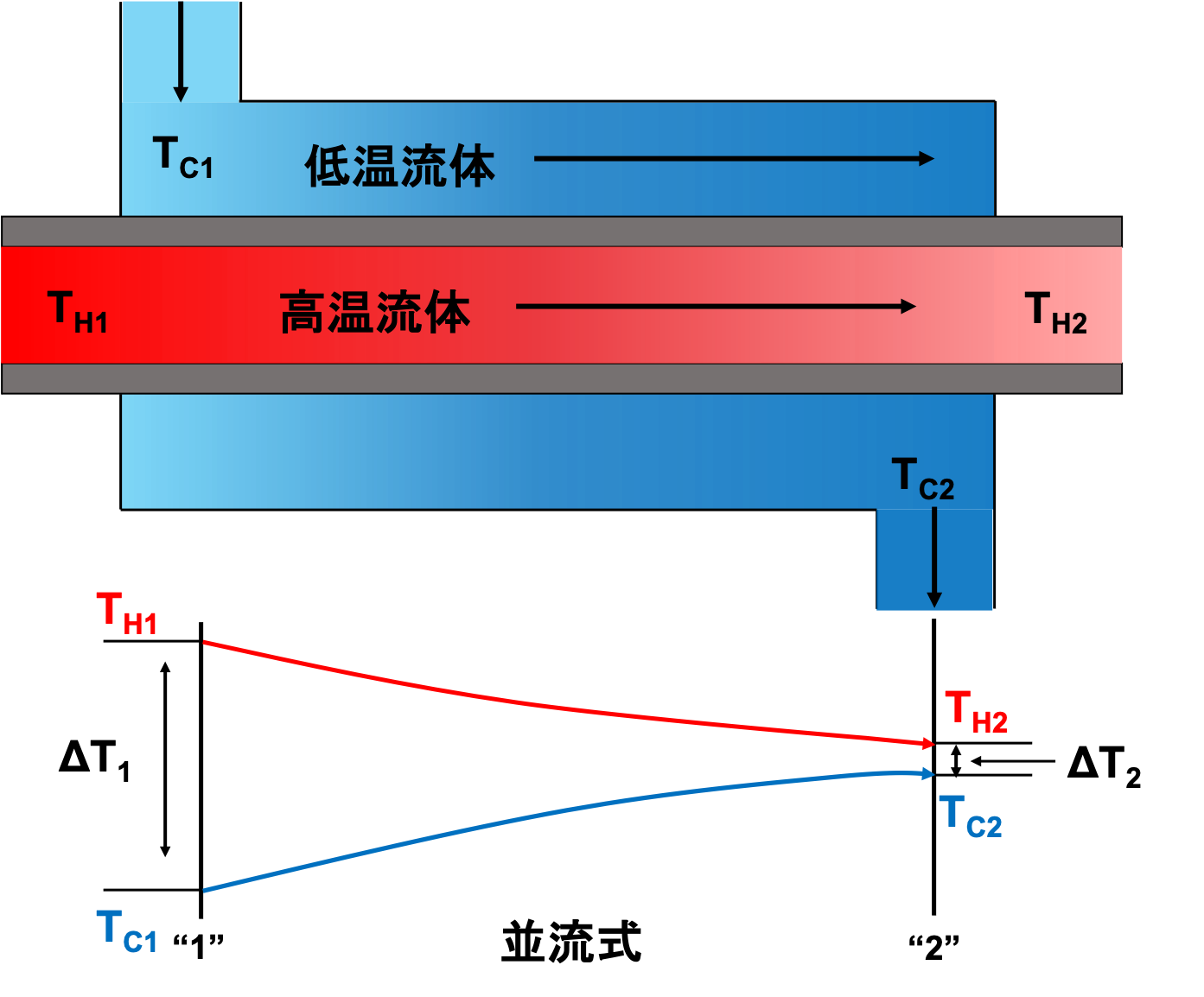熱交換器では、高温流体と低温流体の温度差\(\Delta T \)が位置によって異なります。
よって、熱交換器全体の"平均"温度差を考える必要があり、そこで登場するのが対数平均温度差\(\Delta T_{lm}\)です。
対数平均温度差
$$\Delta T_{lm} = \frac{\Delta T_1 - \Delta T_2}{\ln \left(\frac{\Delta T_1}{\Delta T_2}\right)}\tag{15}$$
対数平均温度差\(\Delta T_{lm}\)の計算方法や、なぜ対数平均を用いるのかについては、下の記事でわかりやすく解説しました。
-
-
【例題でわかる】対数平均温度差（LMTD）の計算方法
続きを見る
まとめ
まとめ
- 総括伝熱係数\(U\)は、3つの熱移動を総括した伝熱係数のこと
- 総括伝熱係数と伝熱面積の積の逆数\(\dfrac{1}{UA}\)を総括伝熱抵抗と呼ぶ
- オームの法則のアナロジーを考えると、温度差\(\Delta T\)が電圧\(E\)、伝熱抵抗\(\dfrac{1}{UA}\)が抵抗\(R\)、伝熱量\(Q\)が電流\(I\)に該当する
- 直列の伝熱抵抗は足し算できる
⇒熱交換器の伝熱抵抗は、各熱移動の伝熱抵抗と汚れ係数の和で表される。 - 熱交換器は、各熱移動における伝熱面積が異なるため、基準の伝熱面積を置く
- 熱交換器の温度差は、対数平均温度差\(\Delta T_{lm}\)を用いる
参考文献
1．基礎化学工学
本記事を書く際に、最も参考にしました。
できる限り易しく解説していますが、かゆいところに手が届く記述でとても重宝しました。
現代化学工学が難しいと感じる方におすすめの教科書です。
熱交換器を設計するならば、確実に手元に置いておきたい1冊です。
例題が豊富なので、似たような熱交換器の例題を参考にできます。
amazonでは在庫切れで買えませんが、理工学図書出版のホームページで注文することができます。
