どうも。こんにちは。
ケミカルエンジニアのこーしです。
本日は、「Borutaによる変数(特徴量)選択」についてわかりやすく解説します。
回帰分析の精度を上げるために、重要でない説明変数を除外することは大切です。
Borutaは、ランダムフォレストの重要度に基づいた変数選択手法であり、直感的で使いやすく、初心者から上級者まで幅広いユーザーが利用できるのも大きな魅力です。
本記事を読めば、強力な変数選択手法であるBorutaが簡単に実装できるようになります!
本記事の内容
・Borutaとは
・サンプルデータの入手
・【Python】Borutaによる変数選択
・回帰分析結果
・参考文献
目次
Borutaとは
代表的な変数選択手法として、ステップワイズ法やLASSO、遺伝的アルゴリズム(GA)などがあります。
これらの変数選択手法では、決定係数R2やRMSE、MAEなどの統計量を最適化するように説明変数(特徴量)を選択します。
しかし、これらの統計量を最適化できても、その指標に過学習してしまう可能性があります。
そこで、ランダムフォレストの重要度に基づいて変数選択するBorutaという手法が注目を浴びています。
Borutaのアルゴリズム
Borutaのアルゴリズムは下記の通りです。
Borutaのアルゴリズム
- 元のデータセット\(X\)をコピー
- コピーしたデータセットの特徴量の値をランダムに並び替えてシャドウ特徴量を作成
- 元のデータセット\(X\)とシャドウ特徴量を結合し、目的変数\(y\)との間でランダムフォレストモデルを作成
- ランダムフォレストで各特徴量(元の特徴量とシャドウ特徴量)の重要度を計算
- 最も重要度の高いシャドウ特徴量と元の特徴量の重要度を比較
- 元の特徴量の重要度の方が高い場合はその特徴量を残し(1とする)、低い場合はその特徴量を削除(0とする)
※pパーセンタイル(perc)が100のとき、シャドウ特徴量の重要度の最大値が基準値となる - 上記1〜6を繰り返し、0,1の二項分布に基づく両側検定(デフォルトα=0.05)で、元の特徴量の方がシャドウ特徴量より重要かどうかを判断
- シャドウ特徴量より重要と判断された元の特徴量を残す
ランダムフォレストの重要度
下式は、j番目の特徴量で分割されたノード\(t\)における重要度です。
$$\frac{n_t}{n}\Delta E_t \tag{1}$$
ここで、\(\Delta E_t\)は、ノード\(t\)においてサンプルを分割したことによる評価関数\(E_i\)の変化です。
ちなみに、回帰分析における評価関数\(E_i\)は目的変数\(y\)の誤差の二乗和です。
$$E_i = \sum (y - \bar{y})^2\tag{2}$$
よって、(1)式をすべての決定木、すべてのノードで足し合わせると、j番目の特徴量の重要度が計算できます。
$$I_j = \frac{1}{k}\sum_{T}\sum_{t \in T,j}\frac{n_t}{n}\Delta E_t \tag{3}$$
- \(k\):決定木の数(サブデータセットの数)
- \(n\):サンプル数
- \(T\):ある決定木
- \(t\):\(T\)におけるノード
- \(\Delta E_t\):ノード\(t\)においてサンプルを分割したことによる評価関数\(E\)の変化
【参考記事】
ランダムフォレスト(Random Forests, RF)~アンサンブル学習で決定木の推定性能を向上!
過学習を防ぐ仕組み
ランダムフォレスト(アンサンブル学習)
ランダムフォレストは、多数の決定木モデルを作成してその多数決を取る手法であるため、「過学習しにくい」という特徴があります。
ちなみに、Borutaを理解するためには、ランダムフォレストを十分理解しておく必要があります。
ランダムフォレストについては、下記の記事で詳しく解説していますので、不安な方はこちらを先に読んでみてください。
-

-
【Python】決定木とランダムフォレストによる重回帰分析
続きを見る
シャドウ特徴量
シャドウ特徴量はランダムに生成されるため、目的変数\(y\)に対して無関係となります。
もし、シャドウ特徴量の重要度が高いという場合は、モデルが「ノイズ」や「無関係なパターン」に過剰に適合していることを意味します。
そこで、シャドウ特徴量よりも高い重要度を持つ元の特徴量のみを選択することで、モデルがランダムな「ノイズ」に適合することを防ぎ、過学習のリスクを低減します。
特徴量の数の調整方法
Borutaにもハイパーパラメータが存在します。
ハイパーパラメータを調整することで、選択される変数(特徴量)の数を微調整することができます。
やり方としては、大きく下記2つの方法があります。
1. シャドウ特徴量の重要度のパーセンタイル(perc)
元の特徴量の重要度がシャドウ特徴量の「どのパーセンタイル」を上回る必要があるかを設定します。
例えば、pパーセンタイル( perc)が100(デフォルト)のときは、シャドウ特徴量の重要度の最大値(100%)が基準値となります。
percを100から小さくすると、より多くの特徴量が選択される傾向があります。
pパーセンタイルについては、下記記事の解説がわかりやすいです。
2. 二項分布に基づく両側検定の有意水準(alpha)
二項分布に基づく両側検定の有意水準(alpha)を設定します。
例えば、デフォルトである0.05に対して0.1とかに大きくすると、選択される特徴量が増える傾向があります。
サンプルデータの入手
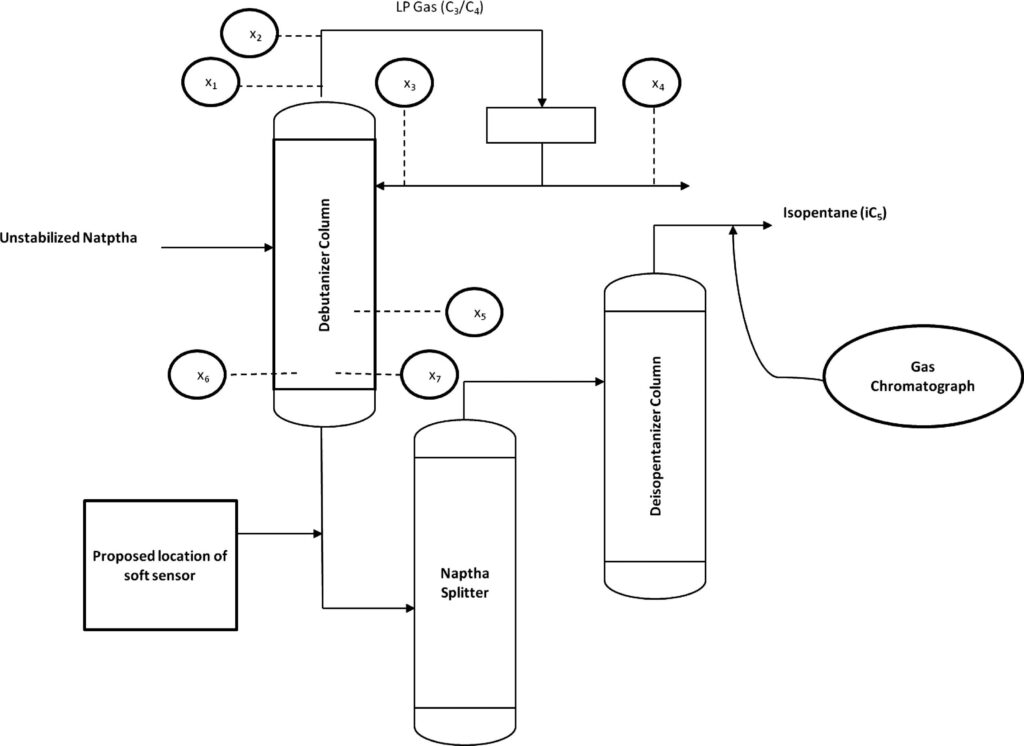
コチラのGitHubページで入手できる「debutanizer_data.csv」を利用します。
脱ブタン塔のプロセスデータであり、プロセスフローは上図の通りです。
説明変数がx1〜x7の7個で、目的変数がyの1個、サンプル数は2394個です。
| 変数名 | 詳細 | 日本語訳 |
|---|---|---|
| x1 | Top Temperature | 塔頂温度 |
| x2 | Top pressure | 塔頂圧力 |
| x3 | Reflux flow | 還流流量 |
| x4 | Flow to next process | 次プロセスへの流量 |
| x5 | 6th tray Temperature | 6段目温度 |
| x6 | Bottom Temperature1 | 塔底温度1 |
| x7 | Bottom Temperature2 | 塔底温度2 |
| y | Butane(C4) content in the debutanizer column bottom | 塔底におけるブタン含有量 |
データの読み込み
「debutanizer_data.csv」と同じフォルダに、「boruta.ipynb」というファイルを作成しましょう。
下記のコードでライブラリのインポートと、データの読み込みを行います。
ここでは、下記3つのデータの前処理を行っています。
- 時系列データなので、実務データを想定しインデックスに時刻を割り振る
- 目的変数yの測定時間を考慮し、5分(行)だけデータをずらす
- プロセス知見より、目的変数yと説明変数x1〜x7の時間差を18分とする(時間遅れ変数の作成)
import math import numpy as np import pandas as pd import matplotlib.pyplot as plt import matplotlib.dates as mdates from sklearn import metrics from sklearn.preprocessing import StandardScaler from sklearn.model_selection import train_test_split, cross_val_predict, KFold from sklearn.ensemble import RandomForestRegressor from boruta import BorutaPy
#脱ブタン塔のプロセスデータを読み込む
df = pd.read_csv('debutanizer_data.csv')
#時系列データなので、実務データを想定しindexに時刻を割り当てる
# 開始日時を指定
start_datetime = '2024-01-01 00:00:00'
# DataFrameの長さを取得
n = len(df)
# 日時インデックスを生成(1分間隔)
date_index = pd.date_range(start=start_datetime, periods=n, freq='T')
# DataFrameのインデックスを新しい日時インデックスに設定
df.index = date_index
# 目的変数の測定時間を考慮(5分間)
df['y'] = df['y'].shift(5)
#yがnanとなる期間のデータを削除
df = df.dropna()
#説明変数と目的変数にわける
X = df.iloc[:, :-1]
y = df['y']
#時間遅れ変数を作成
delay_number = 18
X_with_delays = pd.DataFrame()
for col in X.columns:
col_name = f"{col}_delay_{delay_number}"
X_with_delays[col_name] = X[col].shift(delay_number)
# 時間遅れ変数とyのデータフレームを作成
X_with_delays['y'] = y
X_with_delays = X_with_delays.dropna()
# 目的変数と説明変数に分割
X = X_with_delays.iloc[:, :-1]
y = X_with_delays['y']
ここで、変数選択を実演するために、ダミー変数を作成しておきます。
元の説明変数は7変数でしたが、ダミー変数を追加して17変数になりました。
# データの標準化
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)
X_scaled = pd.DataFrame(X_scaled, index=X.index, columns=X.columns)
y_scaled = scaler.fit_transform(y.values.reshape(-1, 1)).ravel()
y_scaled = pd.Series(y_scaled)
# ランダムで作成した説明変数を10個追加
np.random.seed(0)
for i in range(1, 11):
X_scaled[f'random_var{i}'] = np.random.randn(len(X_scaled))
【Python】Borutaによる変数選択
それでは、実際にBorutaによる変数選択を実行しましょう。
#変数選択
def boruta(X, y, n_jobs=-1, max_depth=5, verbose=2, random_state=0):
"""
RandomForestaRegressorでBorutaを実行
パラメータ
----------
X:説明変数(pd.Dataframe)
y:目的変数(pd.Dataframe,Series)
n_jobs:デフォルト-1
max_depth:デフォルト5
verbose:デフォルト2
random_state:デフォルト0
戻り値
----------
X:変数選択後のデータセット
selected_val:変数選択後の説明変数
"""
rf = RandomForestRegressor(n_jobs=n_jobs, max_depth=max_depth, random_state=random_state, min_samples_leaf=5)
feat_selector = BorutaPy(rf, n_estimators= 'auto', perc=100, alpha=0.05, verbose=verbose, random_state=random_state)
feat_selector.fit(X.values, y.values.astype(int))
# 選択された特徴量を確認
selected = feat_selector.support_
print('選択された特徴量の数: %d' % np.sum(selected))
print(selected)
print(X.columns[selected])
X_boruta = X[X.columns[selected]] # 説明変数
return X_boruta, selected
# 関数の実行
X_boruta, selecetd_val = boruta(X_scaled, y_scaled)
Borutaによる変数選択の結果、ランダムで作成したダミー変数が全て除外されていました。
回帰分析結果
変数選択前後のデータセットを使って回帰分析(ランダムフォレスト)を実行してみましょう。
回帰分析用のモジュールをregression_tools.pyにまとめておきました。
GitHubリンク(regression_tools.py)
regression_tools.pyを本ファイルと同じフォルダに置き、importしましょう。
import regression_tools as rt # ランダムフォレスト回帰(ブランク) optimal_x_variables_rate, rf_final = rt.perform_rf_regression(X, y) # ランダムフォレスト回帰(Boruta) optimal_x_variables_rate, rf_final = rt.perform_rf_regression(X_boruta, y)
図はGitHubの方に掲載しているため省略しますが、結果は下表に示します。
| 変数選択なし 17変数 | R2 | RMSE | MAE |
| トレーニングデータ | 0.715 | 0.075 | 0.055 |
| テストデータ | 0.543 | 0.123 | 0.092 |
| 変数選択あり(Boruta) 7変数 | R2 | RMSE | MAE |
| トレーニングデータ | 0.726 | 0.074 | 0.054 |
| テストデータ | 0.563 | 0.121 | 0.090 |
わかりにくいですが、説明変数(特徴量)の数が半減以下になっても、予測精度が向上しているようです。
Borutaは、非常に簡単なコードで実装でき、ハイパーパラメータも少ないため、初心者でも扱える有用な変数選択手法です。
ぜひBorutaを身につけて、回帰分析の予測精度を上げていきましょう!
参考文献
Borutaの解説はこちらを参照しました。
金子先生の書籍の中でも難しめのものになります(中級向け)。
Pythonで学ぶ実験計画法入門 ベイズ最適化によるデータ解析
ランダムフォレストによる回帰分析は、こちらの書籍を参考にしました。
ランダムフォレストによる「分類」の解説はよく見かけますが、回帰分析について解説している書籍はレアです。
ランダムフォレスト(Random Forests, RF)~アンサンブル学習で決定木の推定性能を向上!
ランダムフォレストの重要度は、コチラの記事を参考にしました。
BorutaPyの中身はコチラのページを参考にしました。
設定すべきハイパーパラメータは、ドキュメント見て確認した方が良いですね。

