どうも。こんにちは。
ケミカルエンジニアのこーしです。
本日は、「ヒストグラムの作成方法(スタージェスの公式)」についてわかりやすく解説します。
データを取り扱う際、ヒストグラムを作成してデータの分布を確認することは重要です。
しかし、「階級幅」もしくは、「ビン数」を適切に設定しないと、正しくデータの分布を理解することはできません。
そこで本記事では、Pythonを使ってヒストグラムを作成する際に、ビン数を適切に決める方法についても詳しく解説します。
これらの手法を使えば、データの特徴を正確に捉えることができます。
本記事の内容
・ヒストグラムの作成方法
・スタージェスの公式
・簡易手法(サンプル数の0.5乗)
・スタージェスの公式 v.s 簡易手法
・参考文献
この記事を書いた人
 こーし(@mimikousi)
こーし(@mimikousi)
目次
ヒストグラムの作成方法
まず、ヒストグラムを作成するためのサンプルデータを入手しましょう。
サンプルデータの入手
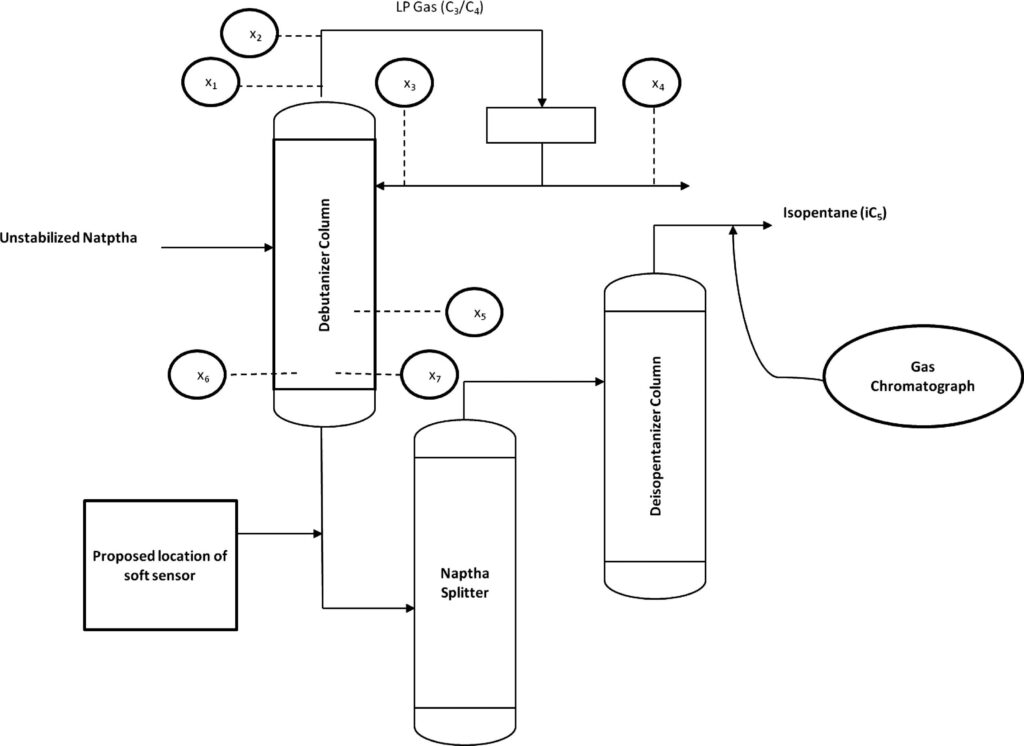
コチラのGitHubページで入手できる「debutanizer_data.csv」を利用します。
脱ブタン塔のプロセスデータであり、プロセスフローは上図の通りです。
説明変数がx1〜x7の7個で、目的変数がyの1個、サンプル数は2394個です。
| 変数名 | 詳細 | 日本語訳 |
|---|---|---|
| x1 | Top Temperature | 塔頂温度 |
| x2 | Top pressure | 塔頂圧力 |
| x3 | Reflux flow | 還流流量 |
| x4 | Flow to next process | 次プロセスへの流量 |
| x5 | 6th tray Temperature | 6段目温度 |
| x6 | Bottom Temperature1 | 塔底温度1 |
| x7 | Bottom Temperature2 | 塔底温度2 |
| y | Butane(C4) content in the debutanizer column bottom | 塔底におけるブタン含有量 |
ヒストグラムの作成
では早速、pythonでデータを読み込み、ヒストグラムを作成しましょう。
「debutanizer_data.csv」と同じフォルダに「histogram.py」を作成し、下記のコードを入力します。
import pandas as pd
import matplotlib.pyplot as plt
import numpy as np
from scipy.stats import norm
from matplotlib.backends.backend_pdf import PdfPages
# ファイルの読み込み
df = pd.read_csv('debutanizer_data.csv')
#pdfで保存するためpdfインスタンスを作成
pdf = PdfPages('histogram_debutanizer.pdf')
# binの数
num_bins = 20
# 列ごとにヒストグラムを作成
for col in df.columns:
# グラフの設定
fig, ax = plt.subplots(figsize=(8, 5))
# ヒストグラムの表示(density=Trueで密度表示)
ax.hist(df[col], bins=num_bins, density=True, alpha=0.7, label='Histogram')
# 正規分布のパラメータの推定
mu, sigma = norm.fit(df[col])
# 正規分布曲線のx値の範囲を決定
x = np.linspace(df[col].min(), df[col].max(), 100)
# 正規分布曲線の描画
ax.plot(x, norm.pdf(x, mu, sigma), 'r-', label='Normal Distribution')
ax.set_title(col)
ax.set_xlabel(f'{col}_value')
ax.set_ylabel('Frequency')
ax.legend()
# グラフを保存
fig.savefig(f'{col}_histogram.png')
pdf.savefig(fig)
plt.close(fig)
#close処理
pdf.close()
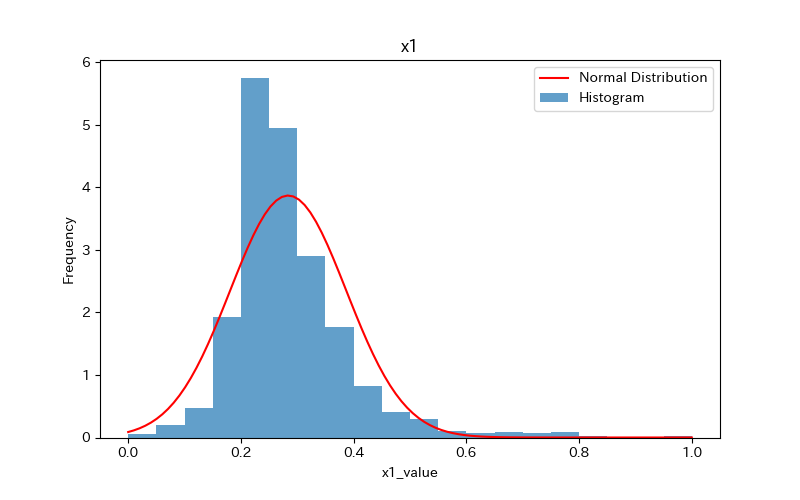
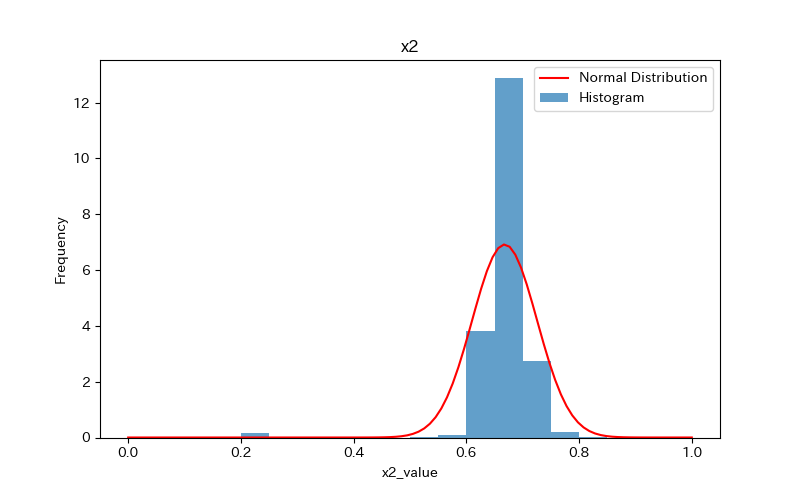
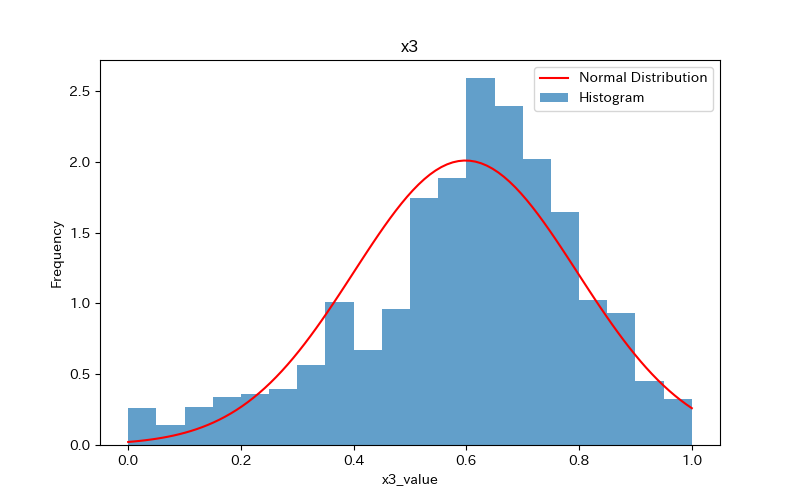
上記のコードによりx1〜x7、yのヒストグラムが作成されます。
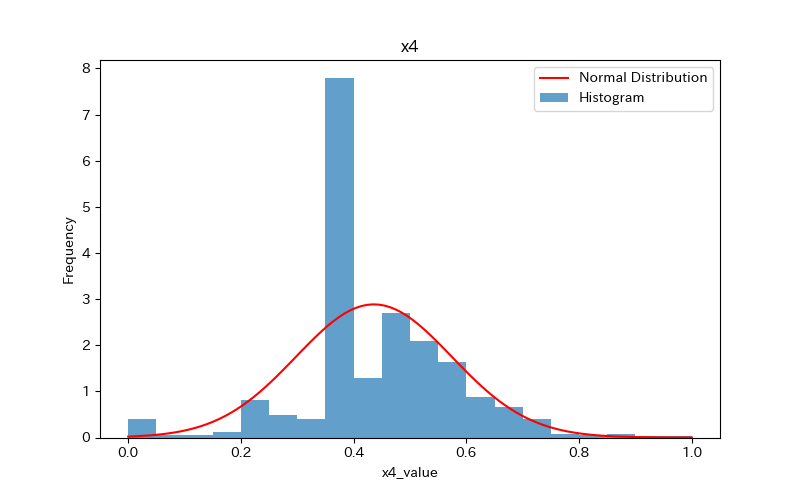
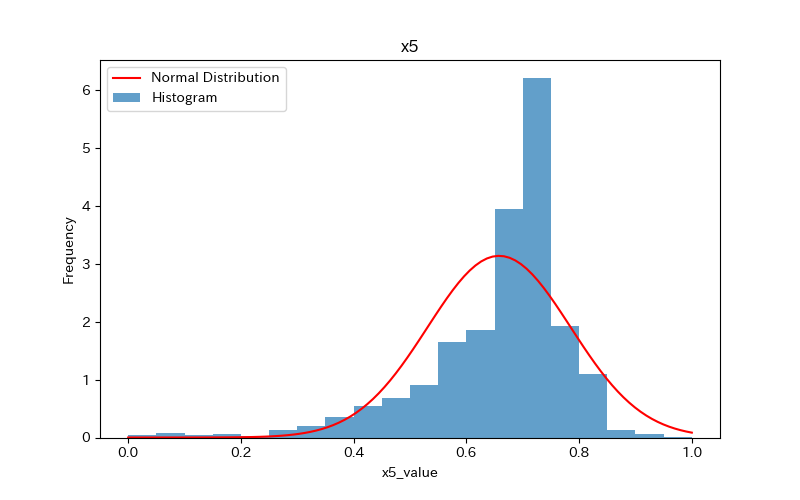
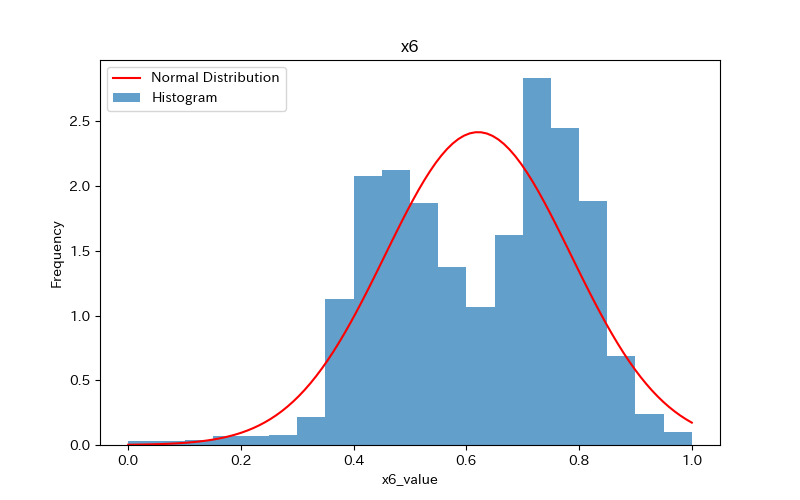
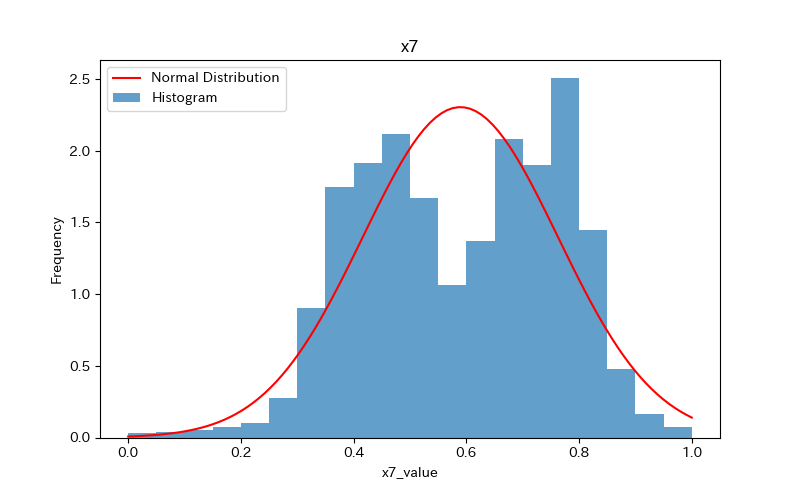
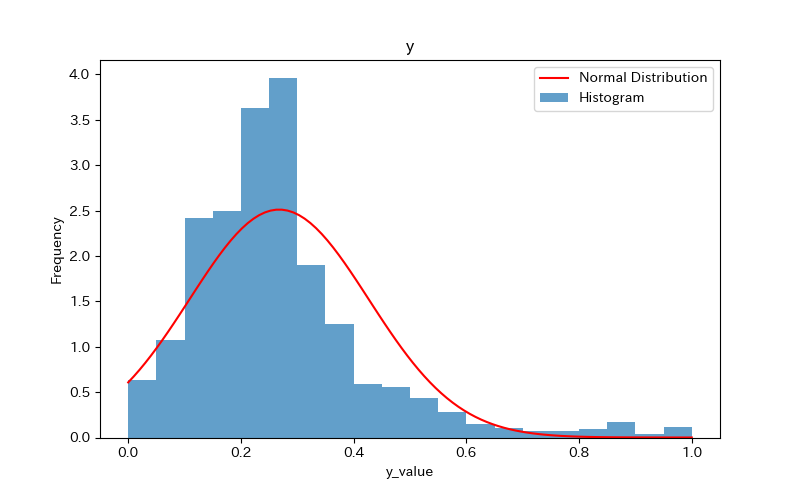
コードの解説
上記のコードを簡単に解説していきます。
1.ライブラリのインポート
まず、必要なライブラリをインポートします。
pandas:データフレームの操作を行うためのライブラリmatplotlib.pyplot:グラフの描画を行うためのライブラリnumpy:数値計算を行うためのライブラリscipy.stats.norm:正規分布の統計的な処理を行うためのライブラリ
2.CSVファイルの読み込み
続いて、pd.read_csv()関数を使用して、指定されたCSVファイルをデータフレームとしてdfに格納します。
データフレームは、表形式のデータを扱うためのオブジェクトです。
3.pdfインスタンスの作成
PDFファイルにグラフを保存するためにpdfインスタンスを作成します。
4.ビンの数の設定
num_binsという変数を使用して、ヒストグラムの縦棒(ビン)の数を指定します。
この値が大きいほど、ヒストグラムの詳細度が増えます。
5.列ごとにヒストグラムと正規分布曲線を作成
forループを使用して、データフレームの各列に対して以下の処理を繰り返します。
-
- グラフの図と軸を作成
plt.subplots()関数でグラフの図(fig)と軸(ax)を作成します。
引数figsize=()でグラフのサイズを指定できます。 - ヒストグラムを描画
ax.hist()関数を使用して、ヒストグラムを描画します。
density=Trueとすることで、ヒストグラムの面積が1になり、確率密度関数として解釈できます(正規分布曲線と比較するためです)。
alphaは、ヒストグラムの透明度を設定するパラメータです。 - 正規分布のパラメータ(平均と標準偏差)を推定
norm.fit()は、正規分布に従うデータに対して、最尤推定法を用いて「平均」と「標準偏差」のパラメータを推定する関数です。 - xの範囲を決定
np.linspace()関数を使用して、データの最小値から最大値までの範囲を等間隔に分割します。 - 正規分布曲線の描画
ax.plot()関数を使用して、x値に対応する正規分布の確率密度関数を描画します。
'r-'は赤色の実線を意味します。 - グラフのタイトル、x軸ラベル、y軸ラベルを設定
ax.set_title()でグラフのタイトルを指定します。
ax.set_xlabel()でx軸の名称を指定します。
ax.set_ylabel()でy軸の名称を指定します。 - 凡例を表示
ax.legend()により、ヒストグラムと正規分布曲線の対応関係を示します。 - グラフの保存
fig.savefig(f'{col}_histogram.png')でグラフを画像ファイルとして保存します。
同様に、pdf.savefig(fig)でグラフをPDFファイルとして保存します。
plt.close(fig)でグラフを閉じます。 - close処理
pdf.close()でPDFファイルを閉じます。
- グラフの図と軸を作成
ビン数が不適切な場合
ヒストグラムの縦棒(ビン)の数が不適切だと、データの分布を正しく読むことができません。
そこで、x6を例に、ビン数を5、20、50に変更してみます。
ビン数=5
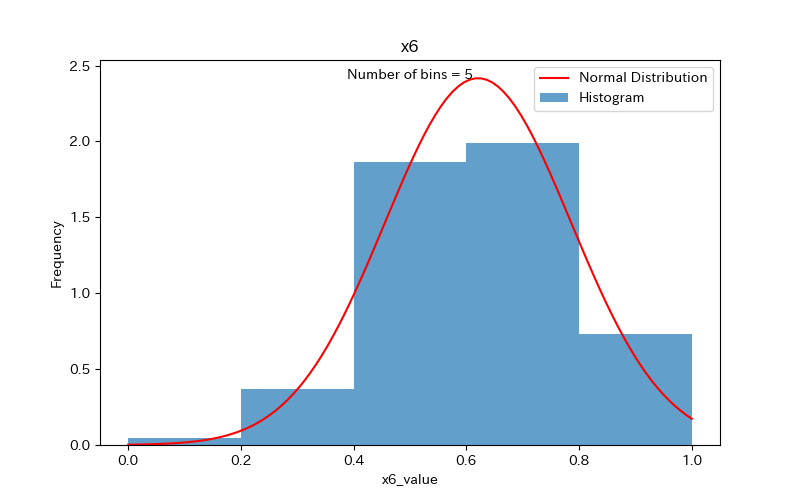
ビン数=20
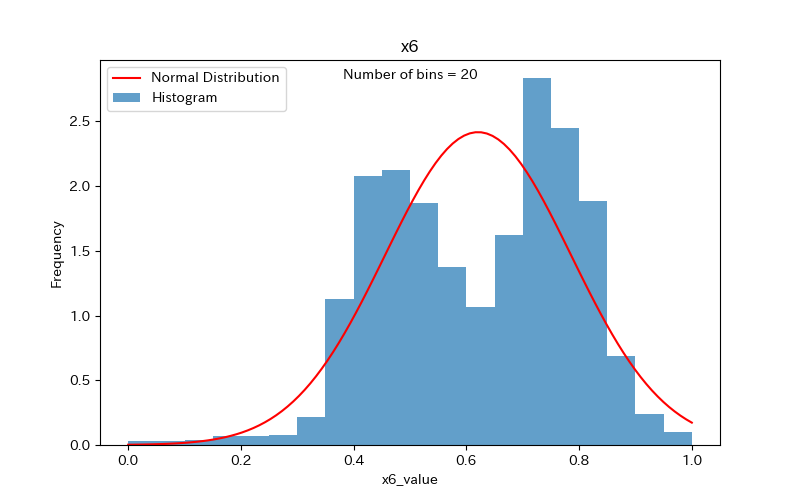
ビン数=50

x6のデータ分布は、本来2つの山があります。
しかし、ビン数を5にすると、それが読み取れなくなることがわかります。
よって、データの分布を正しく理解するためには、ビン数を適切に設定する必要があります。
ビン数の決定方法
ヒストグラムの縦棒(ビン)の数の決定方法には、いくつかの方法があり、本記事では「スタージェスの公式」と「簡易手法」の2通りを紹介します。
スタージェスの公式
スタージェスの公式は、データが正規分布に近い場合やデータ数が多い場合に有用です。
スタージェスの公式は下式のように表されます。
$$k = 1 + \rm{log}2(N)$$
ここで、kは推定されたビンの数であり、Nはデータのサンプル数です。
簡易手法(サンプル数の0.5乗)
簡易手法は、サンプル数の0.5乗をビンの数に指定する方法です。
ビンの数をk = √Nとして計算します。
ここで、kは推定されたビンの数であり、Nはデータのサンプル数です。
スタージェスの公式 v.s 簡易手法
サンプル数とビンの数の関係
サンプル数(N)に応じて、ビンの数(k)がどのように対応するのか、スタージェスの公式と簡易手法で比較してみました。
スタージェスの公式は、サンプル数30くらいまではビン数が大きく変動しますが、サンプル数が30を超えてくると、なだらかに増加します。
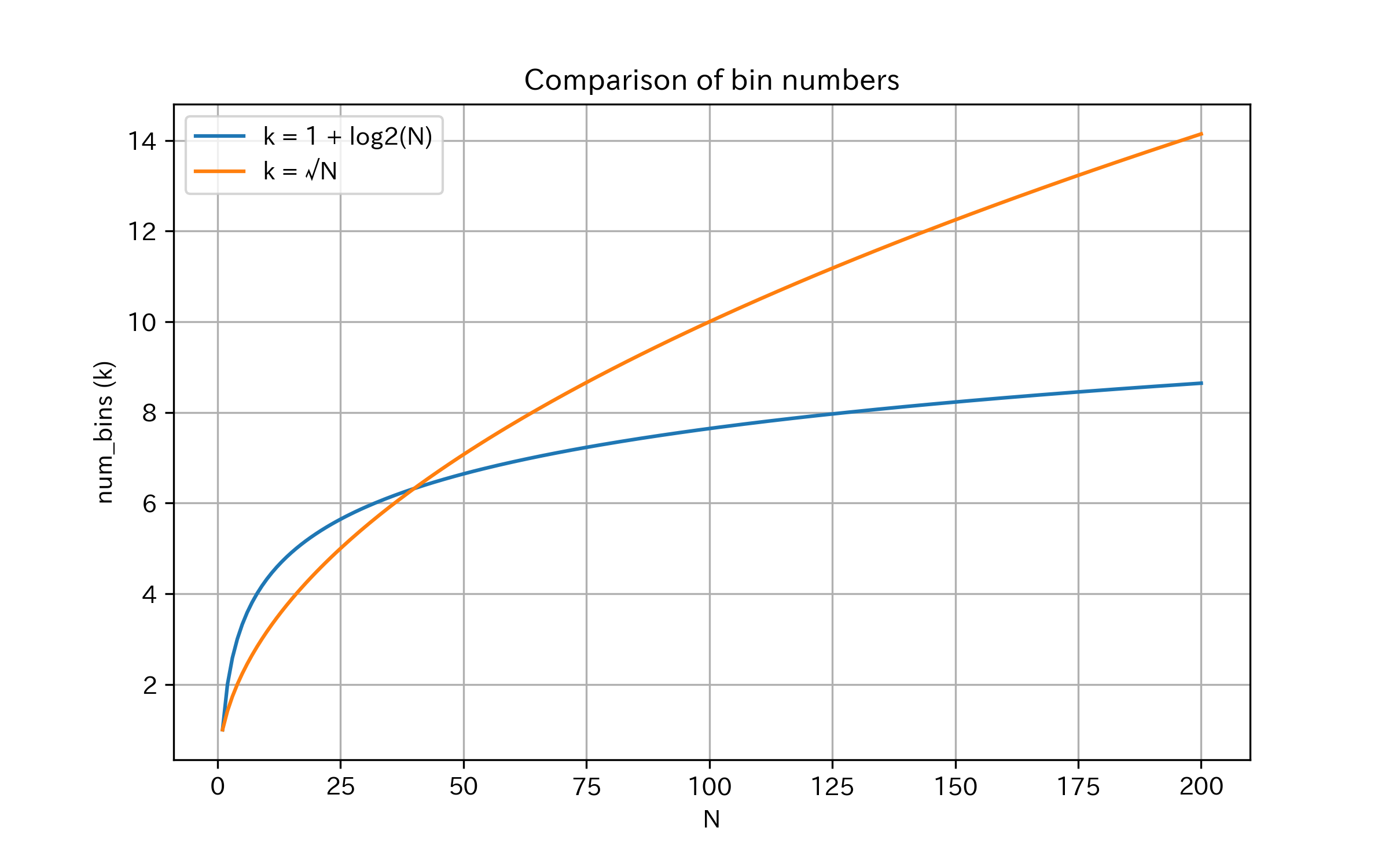
ヒストグラムの比較
サンプル数が2394個なので、ビンの数は下記の通りです。
- スタージェスの公式:12個
- 簡易手法(0.5乗): 48個
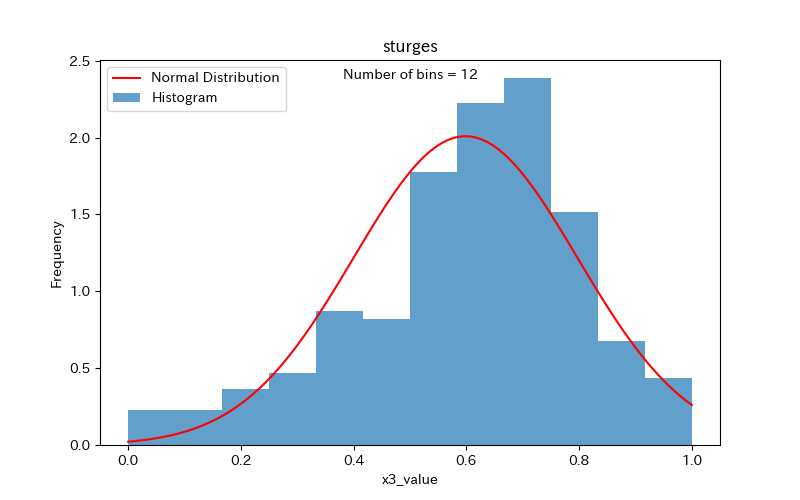
まず、x3のヒストグラムで比較してみましょう。
スタージェスの公式の方がまとまりがある感じで、簡易手法だと縦棒(ビン)の数が多すぎるように見えます。
スタージェスの公式
簡易手法
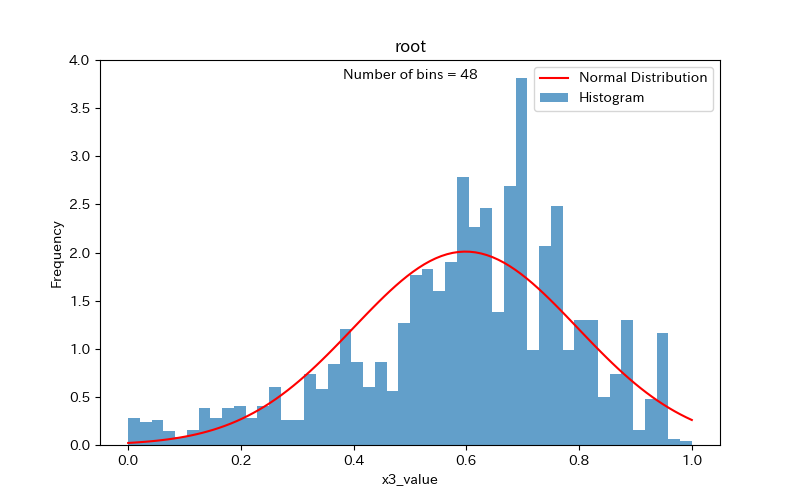
続いて、x6でも比較してみましょう。
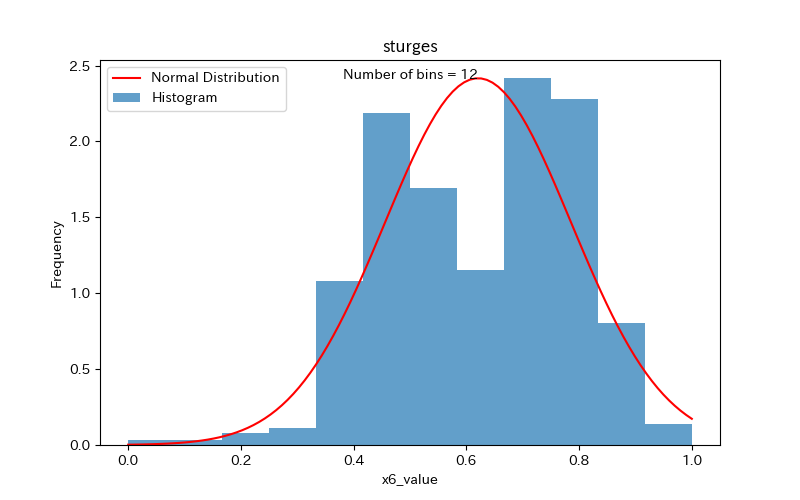
x6は分布が二つの山にわかれており、簡易手法の方がより正確にデータの特徴を捉えているように見えます。
スタージェスの公式は、データ分布が正規分布に近い場合に有用であるため、分布が二つに分かれている場合には注意が必要ですね。
スタージェスの公式
簡易手法
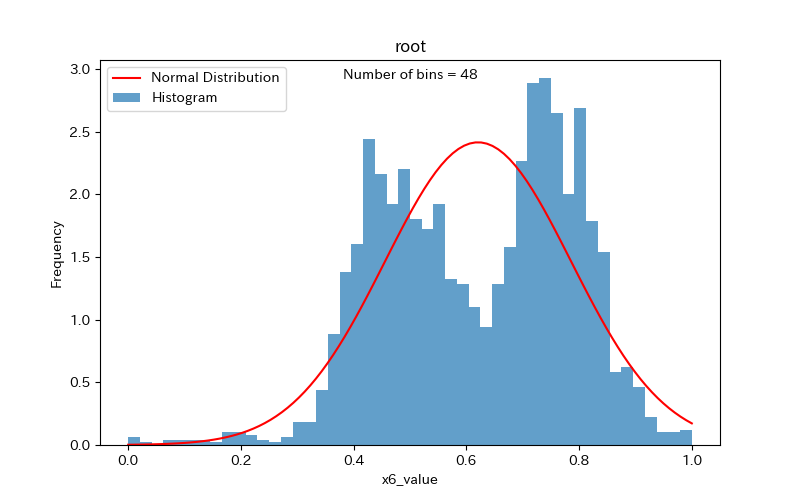
コード例
スタージェスの公式
まず、スタージェスの公式を使ってビンの数を計算しましょう。
列ごとにヒストグラムを作成するforループ以降を下記の通り書き直します。
#pdfで保存するためpdfインスタンスを作成
pdf = PdfPages('histogram_sturges_debutanizer.pdf')
# 列ごとにヒストグラムを作成
for col in df.columns:
# グラフの設定
fig, ax = plt.subplots(figsize=(8, 5))
# ヒストグラムのbinの数を計算(スタージェスの公式)
num_bins = int(np.log2(df[col].shape[0]) + 1)
# ヒストグラムの表示(density=Trueで密度表示)
ax.hist(df[col], bins=num_bins, density=True, alpha=0.7, label='Histogram')
# ビン数を表示
ax.text(0.5, 0.95, f'Number of bins = {num_bins}', transform=ax.transAxes, ha='center')
# 正規分布のパラメータの推定
mu, sigma = norm.fit(df[col])
# 正規分布曲線のx値の範囲を決定
x = np.linspace(df[col].min(), df[col].max(), 100)
# 正規分布曲線の描画
ax.plot(x, norm.pdf(x, mu, sigma), 'r-', label='Normal Distribution')
ax.set_title('sturges')
ax.set_xlabel(f'{col}_value')
ax.set_ylabel('Frequency')
ax.legend()
# グラフを保存
fig.savefig(f'{col}_histogram_sturges.png')
pdf.savefig(fig)
plt.close(fig)
#close処理
pdf.close()
簡易手法
同様に、forループ以降を下記の通り書き直します。
#pdfで保存するためpdfインスタンスを作成
pdf = PdfPages('histogram_root_debutanizer.pdf')
# 列ごとにヒストグラムを作成
for col in df.columns:
# グラフの設定
fig, ax = plt.subplots(figsize=(8, 5))
# ヒストグラムのbinの数を計算(簡易手法:サンプル数の0.5乗)
num_bins = int(df[col].shape[0] ** 0.5)
# ヒストグラムの表示(density=Trueで密度表示)
ax.hist(df[col], bins=num_bins, density=True, alpha=0.7, label='Histogram')
# ビン数を表示
ax.text(0.5, 0.95, f'Number of bins = {num_bins}', transform=ax.transAxes, ha='center')
# 正規分布のパラメータの推定
mu, sigma = norm.fit(df[col])
# 正規分布曲線のx値の範囲を決定
x = np.linspace(df[col].min(), df[col].max(), 100)
# 正規分布曲線の描画
ax.plot(x, norm.pdf(x, mu, sigma), 'r-', label='Normal Distribution')
ax.set_title('root')
ax.set_xlabel(f'{col}_value')
ax.set_ylabel('Frequency')
ax.legend()
# グラフを保存
fig.savefig(f'{col}_histogram_root.png')
pdf.savefig(fig)
plt.close(fig)
#close処理
pdf.close()
スタージェスの公式や簡易手法は、必ずしも最適なビン数を提供するわけではありません。
他の方法も存在し、データの性質や目的に応じて最適なビン数を選択する必要があります。
まとめ
まとめ
- データを取り扱う際、ヒストグラムを作成してデータの分布を確認することが重要
- 「ビン数」を適切に設定しないと、正しくデータの分布を理解できない
- ビン数の決定方法として、本記事では「スタージェスの公式」と「簡易手法」を紹介
- スタージェスの公式は、サンプル数が多く、データが正規分布に従う場合に有用
- 最適なビン数を提供する方法は確立しておらず、データの性質や目的に応じて調整する必要がある
参考文献
pythonは使いませんが、統計学の基礎を含め、現場で使えるデータ解析手法を学ぶことができます。
本記事で扱った「スタージェスの公式」についても解説されています。
統計学初心者が、現場でデータ解析するための教科書です。
pythonでヒストグラムを作成する方法や、ビン数の決め方として簡易手法(サンプル数の0.5乗)について言及されています。
python初心者でも読みこなせると思います。
