
またネットに載ってるエクセル関数を使って本当に合ってるのかなー?
こんなお悩みを解決します。
どうも。こんにちは。ケミカルエンジニアのこーしです。
本日は、「現場で使えるエクセルによるt検定」について、わかりやすく解説します。
この記事では、実務に沿った例題を使って解説しますので、エクセルによるt検定を身につけることできます。
また、実はt検定には下記2通りの方法があり、今回は【パターン②】p値を用いたt検定を解説します。
p値について理解したい方は、ぜひ読んでみて下さい。

エクセルや統計ソフトを使用しない場合、p値を厳密に求めるのは困難です。
よって、エクセルや統計ソフトを使わない場合は、【パターン①】のt分布表を用いたt検定を行います。
パターン①の検定方法については、下記の記事で解説しています。
また、本記事では割愛しましたが、「帰無仮説」や「有意水準」などの用語についても下記記事で解説しています。
-

-
【例題でわかる】現場で使えるt検定!
続きを見る
本記事の内容
- エクセルを使ったt検定の手順
- p値とは
- 使用するエクセル関数一覧
- t検定の種類
- t検定の例題
①母平均の検定
②平均値の差の検定(独立な2群)
③平均値の差の検定(対応のある2群)
④母分散の差の検定
⑤無相関検定 - 参考文献
この記事を書いた人
 こーし(@mimikousi)
こーし(@mimikousi)
目次
エクセルを使ったt検定の手順(p値を使用)
それでは、エクセルを使ったt検定の手順を見ていきましょう。
t検定の手順(エクセルVer)
- 仮説の設定
帰無仮説\(H_0\)と対立仮説\(H_1\)を設定 - 検定統計量(z,t, Fなど)の算出
- 有意水準の決定
有意水準\(\alpha\)(基本5%)を決める - p値の算出
- 判定
算出したp値が、
・有意水準未満 → 帰無仮説を棄却
・有意水準以上 → 帰無仮説を採択 - 結論
p値とは
p値とは、
「帰無仮説が正しいときに、データから得られた検定統計量(zやt、Fなど)がそれ以上偏った値を取る確率」のことです。
例えば、\(p=0.04\)のとき、それ以上偏ったデータが得られる確率は、4%です。
つまり、\(p=0.04\)とは、帰無仮説が正しいとすると、4%しか起き得ないデータだということです。
そこで、有意水準を\(\alpha = 0.05\)とすると「有意」となりますし、有意水準を\(\alpha = 0.01\)とすると「有意でない」と判断できます。
\(p<\)有意水準\(\alpha\) のとき、帰無仮説を棄却
\(p \geq \)有意水準\(\alpha\) のとき、帰無仮説を採択
図で表すと下図のようになります。
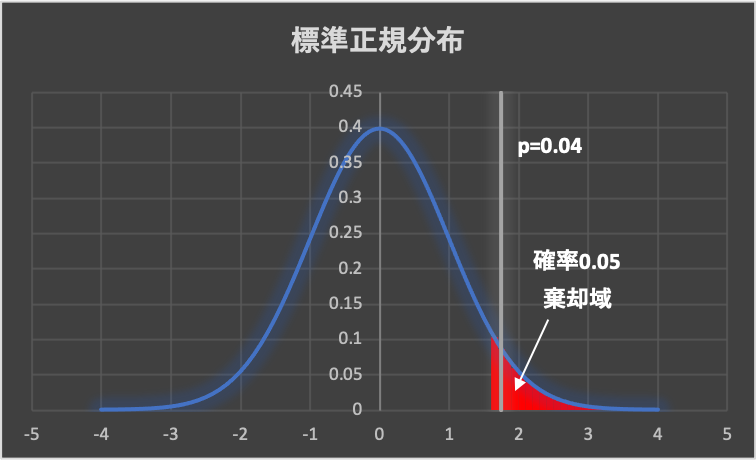
①有意水準\(\alpha =0.05\) のとき(\(p=0.04\))
\(p < 0.05\)となり、p値が棄却域に入るため、帰無仮説を棄却します。
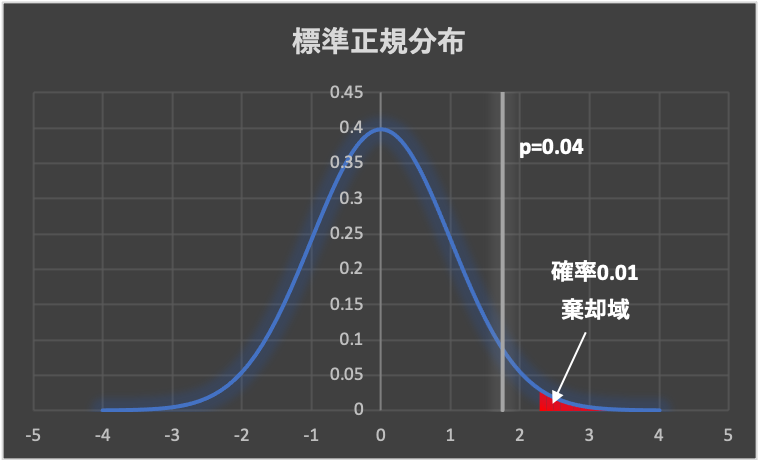
②有意水準\(\alpha =0.01\) のとき(\(p=0.04\))
\(p > 0.01 \)となり、p値が棄却域に入らないため、帰無仮説を採択します。
使用するエクセル関数一覧
使用するエクセル関数の一覧を下表にまとめておきます。
| 関数 | 補足 | |
| 平均 | =AVERAGE('データ範囲を指定') | |
| 母分散\(\sigma^2\) | =VAR.P('データ範囲を指定') | 母集団データの分散であり、自由度はn |
| 標準偏差\(\sigma\) | =STDEV.P('データ範囲を指定') | 母集団データの標準偏差であり、自由度はn |
| 不偏分散\(s^2\) | =VAR.S('データ範囲を指定') | 標本(サンプル)の分散であり、自由度はn-1 |
| 標本標準偏差\(s\) | =STDEV.S('データ範囲を指定') | 標本(サンプル)の標準偏差であり、自由度はn-1 |
| t値 (判断基準) |
=TINV('有意水準' , '自由度(=n-1)') | 有意水準、自由度によって基準のt値が変化 |
| p値 (z検定) |
両側検定のとき =2*(1-NORMSDIST(ABS('データから計算したz値'))) 片側検定のとき =1-NORMSDIST(ABS('データから計算したz値の絶対値')) |
|
| p値 (t検定) |
両側検定のとき =TDIST(ABS('データから計算したt値') , 自由度(=n-1) , 2) 片側検定のとき =TDIST(ABS('データから計算したt値') , 自由度(=n-1) , 1) |
=T.DISTとは別物なので注意 |
| p値 (F検定) |
両側検定のとき =2*FDIST('データから計算したF値' , 分子の自由度(=n1-1) , 分母の自由度(=n2-1)) 片側検定のとき =FDIST('データから計算したF値' , 分子の自由度(=n1-1) , 分母の自由度(=n2-1)) |
=F.DISTとは別物なので注意 |
| p値 (無相関検定) |
両側検定のとき =TDIST(ABS('データから計算したt値') , 自由度(=n-2) , 2) 片側検定のとき =TDIST(ABS('データから計算したt値') , 自由度(=n-2) , 1) |
=T.DISTとは別物なので注意 |
| t検定 | 両側検定のとき =T.TEST('範囲1' , '範囲2' , 1 , '検定の種類' ) 片側検定のとき =T.TEST('範囲1' , '範囲2' , 2 , '検定の種類') |
検定の種類 1:対応のある場合 2:分散が等しいとき 3:分散が等しくないとき(Welchの検定) |
| 相関係数r | =CORREL('データ範囲を指定','データ範囲を指定') |
これらの関数を使って、t検定を行っていきます。
t検定の種類(場合分け)
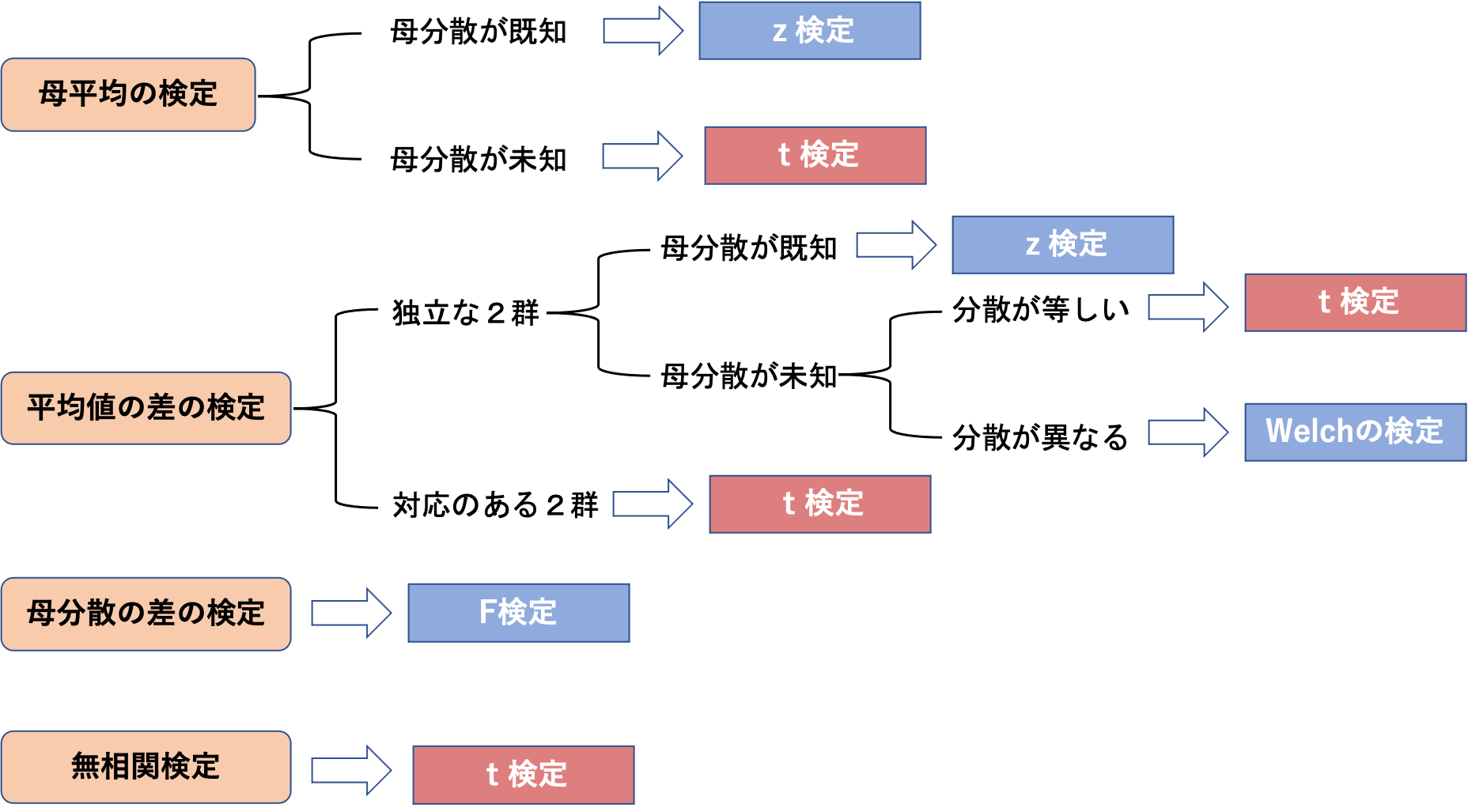
例題を使って解説する前に、t検定の種類について解説しておきます。
t検定には様々な種類があり、上図のような場合分けができます。
1つ1つ例題で解説していきますので、ここで全体像を頭に入れておいてください。
t検定の例題
下記の記事で解説している例題を参考に、本記事ではエクセルを用いてt検定を行います。
-

-
【例題でわかる】現場で使えるt検定!
続きを見る
母平均の検定(母分散が既知の場合)
生産設備(量産機)の品質データなど、大量のデータがある場合は、それらを正規分布に従う母集団とみなし、サンプル(検定したいデータ)の平均が母平均と同じかどうかを検定により判断することができます。
【例題①】品質変化の有無
製品\(A\)の品質(不純物濃度)が変化していないかどうかを検定してみます。
製品\(A\)の不純物濃度の平均値(母平均)が\(\mu_0 = 300\)ppm、母分散が\(\sigma^2 = 8^2\)であったとき、直近生産した製品\(A\)(サンプル)の不純物濃度の平均値が\(\overline{x} = 303\)ppm(n=100)でした。
※標本(サンプル)の分散は母分散と等しいとします。
それでは、検定の手順に従い、例題を解いていきましょう。
例題①は、母分散が既知の場合の母平均の検定ですので、「z検定」です。
よって、検定統計量zが正規分布に従います。
1.仮説の設定
帰無仮説\(H_0 \):\(\mu = 300\) ppm(サンプルの母平均も300ppm)
対立仮説\(H_1 \):\(\mu \neq 300\) ppm(サンプルの母平均は300ppmではない)
大きくても小さくても差があれば、「変化あり」ですので「両側検定」とします。
2.検定統計量の算出
母分散が既知であるため、検定統計量zを使用します。
$$\begin{aligned}z&=\frac{\overline{x}-\mu _{0}}{\frac{\sigma }{\sqrt{n}}}\\[5pt]
&=\frac{303-300}{\frac{8}{\sqrt{100}}}\\[5pt]
&=3.75\end{aligned}$$
3.棄却域の設定
有意水準は、\(\alpha = 0.05\left( 5\% \right)\)とします。
4.p値の算出
p値はエクセルの関数を使って計算します。
z検定では、NORMSDIST関数に、2.で算出したz値の絶対値を代入して、p値を求めます。
両側検定ですので、2倍して有意水準\(\alpha = 0.05\)と比較します。
エクセル関数
p値 = 2*(1 - NORMSDIST(ABS(2.で算出したz値)))
= 2*(1 - NORMSDIST(ABS(3.75)))
= 0.00018
5.判定
\(p=0.00018 < 0.05\)となることから、p値は棄却域に入り、帰無仮説は棄却されます。
6.結論
帰無仮説が棄却されたため、サンプルの母平均は300ppmではなく、すなわち製品\(A\)の不純物濃度は変化していると言えます。

母平均の検定(母分散が未知の場合)
次は、母分散が未知の場合を考えてみましょう。
例えば、母集団となるデータを自社で保有していない場合、母分散は知りようがないので、このケースに該当します。
【例題②】購入品(樹脂)のスペック調査
ガラス転移温度\(T_g\)が100℃の樹脂\(A\)の継続的な購入を検討しています。
ガラス転移温度の平均値\(\mu_0\)が本当に100℃あるのか、検定してみましょう。
サンプル提供(n=20)を依頼し、分析して確かめたところ、平均\(\overline{x}=99\)℃、標本分散が\(s^2 = 3^2\)でした。
ちなみに、標本分散は、偏差平方和をn-1で割ったものです。
$$s^{2}=\frac{1}{n-1}\sum ^{n}_{i=1}\left( x_{i}-\overline{x}\right) ^{2}$$
それでは、検定の手順に従い、例題を解いていきましょう。
樹脂\(A\)は、まだ購入検討段階であり、データが無いため母分散は不明です。(メーカーが開示してくれれば別ですが)
よって、母分散が未知の場合の母平均の検定ですので、「t検定」を行います。
t検定では、検定統計量tがt分布に従います。
1.仮説の設定
帰無仮説\(H_0 \):\(\mu = 100\) ℃(サンプルの母平均も100℃である)
対立仮説\(H_1 \):\(\mu < 100\) ℃(サンプルの母平均は100℃未満である)
ガラス転移温度は、100℃以上であれば問題ないと考えることができるため、今回は「片側検定」とします。
もし、ガラス転移温度が高すぎても良くない場合は、両側検定を行います。
2.検定統計量の算出
母分散が未知であるため、検定統計量tを使用します。
$$\begin{aligned}t&=\frac{\overline{x}-\mu _{0}}{\frac{s }{\sqrt{n}}}\\[5pt]
&=\frac{99-100}{\frac{3}{\sqrt{20}}}\\[5pt]
&=-1.49\end{aligned}$$
3.棄却域の設定
有意水準は、\(\alpha = 0.05\left( 5\% \right)\)とします。
4.p値の算出
p値はエクセルの関数を使って計算します。
t検定では、TDIST関数に、2.で算出したt値の絶対値を代入して、p値を求めます。
t分布は、自由度に応じて変化しますので、自由度(データ数n - 1)を指定します。
また、片側検定ですので、定数1も指定します。
エクセル関数
p値 = TDIST(2.で算出したt値の絶対値, 自由度 n - 1 , 片側検定1 )
= TDIST(ABS(-1.49), 19, 1)
= 0.076
5.判定
\(p=0.076 > 0.05\)となることから、p値は棄却域に入らず、帰無仮説が採択されます。
6.結論
帰無仮説が採択されたため、購入する樹脂のガラス転移温度\(T_g\)は、100℃より低いとは言えない。という結論になります。

平均値の差の検定(独立な2群:母分散が既知の場合)
続いて、独立な2群の平均値の差を検定しましょう。
ある母集団Aと母集団Bの平均値が等しいかどうかを検定します。
独立な2群というのは、母集団Aと母集団Bの間に相関関係が無いということです。
例えば、母集団Aの数値が大きい時に、母集団Bが大きくなる傾向がある場合、それは独立ではなく、後述する「対応のある2群」と見なします。
それでは例題を見てみましょう。
【例題③】量産化製品における原料メーカーの変更
量産化している製品\(A\)の原料を、\(B\)社から\(C\)社に変更しました。
原料メーカーを\(B\)社から\(C\)社に変更した際、製品\(A\)の不純物濃度が変わっているかどうかを検定してみます。
\(B\)社の原料を使って生産した製品\(A\)の不純物濃度の平均値が\(\mu_B = 300\)ppm、母分散が\(\sigma_B^2 = 8^2\)であったとき、\(C\)社の原料を使って生産した製品\(A\)の不純物濃度の平均値が\(\mu_C = 303\)ppm、母分散が\(\sigma_C^2 = 4^2\)でした。
ここで、\(B\)社と\(C\)社共にデータ数は100\(( n_{B}=n_{C}= 100)\)とします。
(量産化製品\(A\)のデータ数は多いため、母集団と見なします。)
それでは、検定の手順に従い、例題を解いていきましょう。
例題③は、母分散が既知の場合の平均値の差の検定ですので、「z検定」です。
よって、検定統計量zが正規分布に従います。
1.仮説の設定
帰無仮説\(H_0 \):\(\mu_B=\mu_C\)(2つの母平均は等しい)
対立仮説\(H_1 \):\(\mu_B \neq \mu_C\)(2つの母平均は等しくない)
大きくても小さくても差があれば、「変化あり」ですので「両側検定」です。
2.検定統計量の算出
母分散が既知であるため、検定統計量zを使用します。
$$\begin{aligned}z&=\frac{\mu _{B}-\mu_{C}}{\sqrt{\frac{\sigma_{B} ^{2}}{n_{B}}+\frac{\sigma _{C}^{2}}{n_{C}}}}\\[5pt]
&=\frac{300-303}{\sqrt{\frac{8^{2}}{100}+\frac{4^{2}}{100}}}\\[5pt]
&=-3.35\end{aligned}$$
3.棄却域の設定
有意水準は、\(\alpha = 0.05\left( 5\% \right)\)とします。
4.p値の算出
p値はエクセルの関数を使って計算します。
z検定では、NORMSDIST関数に、2.で算出したz値の絶対値を代入して、p値を求めます。
両側検定ですので、2倍して有意水準\(\alpha = 0.05\)と比較します。
エクセル関数
p値 = 2*(1 - NORMSDIST(ABS(2.で算出したz値)))
= 2*(1 - NORMSDIST(ABS(-3.35)))
= 0.0008
5.判定
\(p=0.0008 < 0.05\)となることから、p値は棄却域に入り、帰無仮説は棄却されます。
6.結論
帰無仮説が棄却されたため、2つの母平均は等しくないと言えます。
すなわち、原料メーカーが\(B\)社から\(C\)社に変わったことで、製品\(A\)の不純物濃度は変化していると言えます。

平均値の差の検定(独立な2群:母分散が未知の場合①)
次は、母分散が未知の場合を考えます。
ラボ実験や試作機における試作では、データ数が少なく、母集団と見なせるデータ群がありません。
よって、母分散が未知であるとし、検定を行いましょう。
【例題④】試作機における原料メーカーの変更(t検定)
量産化前の試作品\(D\)の原料を、\(E\)社から\(F\)社に変更しました。
原料メーカーを\(E\)社から\(F\)社に変更した際、試作品\(D\)の不純物濃度が変わっているかどうかを検定してみます。
\(E\)社の原料を使って生産した試作品\(D\)の不純物濃度の平均値が\(\overline{x}_E = 300\)ppm、標本分散が\(s_E^2 = 16^2\)であったとき、\(F\)社の原料を使って生産した試作品\(D\)の不純物濃度の平均値が\(\overline{x}_F = 303\)ppm、標本分散が\(s_F^2 = 14^2\)でした。
ここで、\(E\)社品と\(F\)社品共にデータ数は10\(( n_{E}=n_{F}= 10)\)とします。
また、2つの標本分散\(s_E^2\)と\(s_F^2\)は等しいと見なせるとします。※
※本来は、分散が等しいかどうかを別途検定する必要があります。(後述します)
それでは、検定の手順に従って、例題を解いていきましょう。
例題④は、母分散が未知で、2つの標本分散が等しいと見なせるので「t検定」となります。
よって、検定統計量tがt分布に従います。
1.仮説の設定
帰無仮説\(H_0 \):\(\mu_E=\mu_F\)(2つの母平均は等しい)
対立仮説\(H_1 \):\(\mu_E \neq \mu_F\)(2つの母平均は等しくない)
大きくても小さくても差があれば、「変化あり」ですので「両側検定」です。
2.検定統計量の算出
母分散が未知で、2つの標本分散が等しいと見なせるため、下記の検定統計量tを使用します。
$$\begin{aligned}t&=\frac{x_{E}-x_{F}}{s\sqrt{\frac{1}{n_{E}}+\frac{1}{n_{F}}}}\end{aligned}$$
ここで、標本の標準偏差\(s\)を下記のように求めます。
$$\begin{aligned}s&=\sqrt{\frac{s_{E}^{2}\left( n_{E}-1\right) +s_F^{2}\left( n_{F}-1\right) }{n_{E}+n_{F}-2}}\\[5pt]
&=\sqrt{\frac{16^2\left(10-1\right)+14^2\left(10-1\right)}{10+10-2}}\\[5pt]
&=15.03\end{aligned}$$
よって、検定統計量tを計算すると、
$$\begin{aligned}t&=\frac{x_{E}-x_{F}}{s\sqrt{\frac{1}{n_{E}}+\frac{1}{n_{F}}}}\\[5pt]
&=\frac{300-303}{15.03\sqrt{\frac{1}{10}+\frac{1}{10}}}\\[5pt]
&=-0.45\end{aligned}$$
となります。
3.棄却域の設定
有意水準は、\(\alpha = 0.05\left( 5\% \right)\)とします。
4.p値の算出
p値はエクセルの関数を使って計算します。
t検定では、TDIST関数に、2.で算出したt値の絶対値を代入して、p値を求めます。
t分布は、自由度に応じて変化しますので、自由度(\(n_E +n_F - 2\))を指定します。
また、両側検定ですので、定数2も指定します。
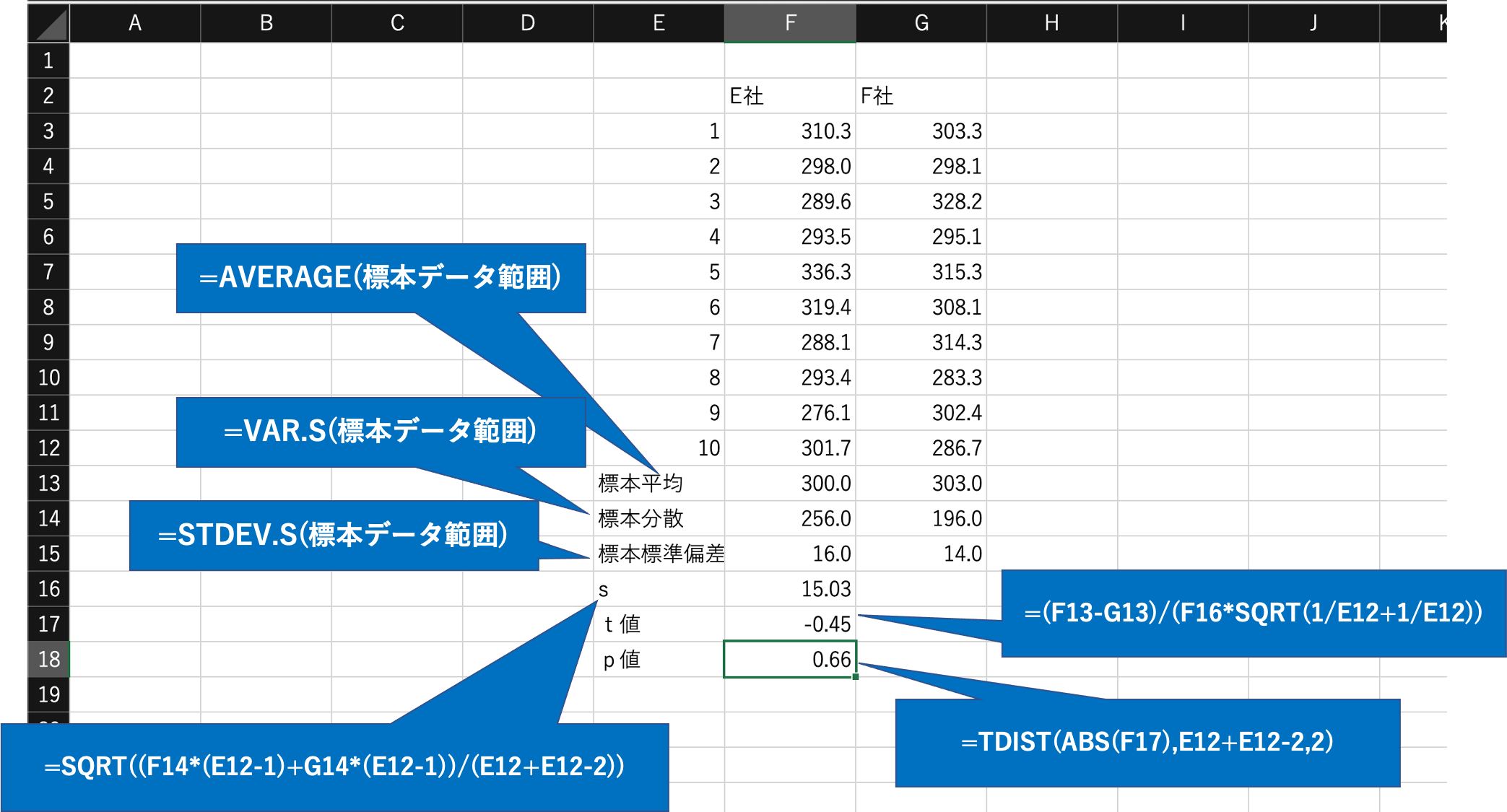
エクセル関数
p値 = TDIST(2.で算出したt値の絶対値, 自由度\(n_E +n_F \) − 2 , 両側検定2 )
= TDIST(ABS(-0.45), 18, 2)
= 0.66
5.判定
\(p=0.66 > 0.05\)となることから、p値は棄却域に入らず、帰無仮説が採択されます。
6.結論
帰無仮説が採択されたため、原料メーカーを変更しても、試作品\(D\)の不純物濃度は変わっているとは言えない。という結論になります。
平均値の差の検定(独立な2群:母分散が未知の場合②)
次は、母分散が未知で、かつ2つの標本分散が等しくない場合の検定について考えましょう。
この検定は、一般にWelchの検定と呼ばれています。
それでは、例題を見ていきましょう。
【例題⑤】試作機における原料メーカーの変更(Welchの検定)
量産化前の試作品\(D\)の原料を、\(E\)社から\(F\)社に変更しました。
原料メーカーを\(E\)社から\(F\)社に変更した際、試作品\(D\)の不純物濃度が変わっているかどうかを検定してみます。
\(E\)社の原料を使って生産した試作品\(D\)の不純物濃度の平均値が\(\overline{x}_E = 300\)ppm、標本分散が\(s_E^2 = 12^2\)であったとき、\(F\)社の原料を使って生産した試作品\(D\)の不純物濃度の平均値が\(\overline{x}_F = 310\)ppm、標本分散が\(s_F^2 = 5^2\)でした。
ここで、\(E\)社品と\(F\)社品共にデータ数は10\(( n_{E}=n_{F}= 10)\)とします。
また、2つの標本分散\(s_E^2\)と\(s_F^2\)は等しくないと見なせるとします。※
※本来は、分散が等しいかどうかを別途検定する必要があります。(後述します)
それでは、検定の手順に従って、例題を解いていきましょう。
例題⑤は、母分散が未知で、2つの標本分散が等しくないと見なせるので「Welchの検定」となります。
t検定と同様、検定統計量tがt分布に従いますが、自由度を特殊な計算で求めます。
1.仮説の設定
帰無仮説\(H_0 \):\(\mu_E=\mu_F\)(2つの母平均は等しい)
対立仮説\(H_1 \):\(\mu_E \neq \mu_F\)(2つの母平均は等しくない)
大きくても小さくても差があれば、「変化あり」となりますので「両側検定」です。
2.検定統計量の算出
母分散が未知で、2つの標本分散が等しくないため、下記の検定統計量tを使用します。
$$\begin{aligned}t&=\frac{\mu_{E}-\mu_{F}}{\sqrt{\frac{s_E^2}{n_{E}}+\frac{s_F^2}{n_{F}}}}\\[5pt]
&=\frac{300-310}{\sqrt{\frac{12^2}{10}+\frac{5^2}{10}}}\\[5pt]
&=-2.43\end{aligned}$$
ここで、自由度\(v\)を下記の通り求めます。
$$\begin{aligned}v&=\frac{( \frac{s_E^2}{n_E}+\frac{s_F^2}{n_F}) ^2}{\frac{s_E^4}{n_E^2(n_E-1)}+\frac{s_F^4}{n_F^2(n_F-1)}}\\[5pt]
&=\frac{(\frac{12^2}{10}+\frac{5^2}{10}) ^2}{\frac{12^4}{100(10-1)}+\frac{5^4}{100(10-1)}}\\[5pt]
&=12.0\end{aligned}$$
よって、自由度\(v=12\)となります。
3.棄却域の設定
有意水準は、\(\alpha = 0.05\left( 5\% \right)\)とします。
4.p値の算出
p値はエクセルの関数を使って計算します。
t検定では、TDIST関数に、2.で算出したt値の絶対値を代入して、p値を求めます。
t分布は、自由度に応じて変化しますので、自由度\(v=12\)を指定します。
また、両側検定ですので、定数2も指定します。
エクセル関数
p値 = TDIST(2.で算出したt値の絶対値, 2.で算出した自由度\(v\) , 両側検定2 )
= TDIST(ABS(-2.43), 12, 2)
= 0.032
5.判定
\(p=0.032 < 0.05\)となることから、p値は棄却域に入り、帰無仮説は棄却されます。
6.結論
帰無仮説が棄却されたため、2つの母平均は等しくないと言えます。
すなわち、原料メーカーが\(E\)社から\(F\)社に変わったことで、試作品\(D\)の不純物濃度は変化していると言えます。

平均値の差の検定(対応のある2群)
これまで、例題③〜⑤では、独立な2群(相関が無い2群)について検定を行ってきました。
今回は、対応のある2群の平均値の差の検定を行います。
【例題⑥】オンライン濃度計の測定値ズレ
ある物質の濃度を測定するオンライン濃度計があります。
新型を購入したため、旧型との測定値のズレがないか確かめるため、平均値検定を行います。
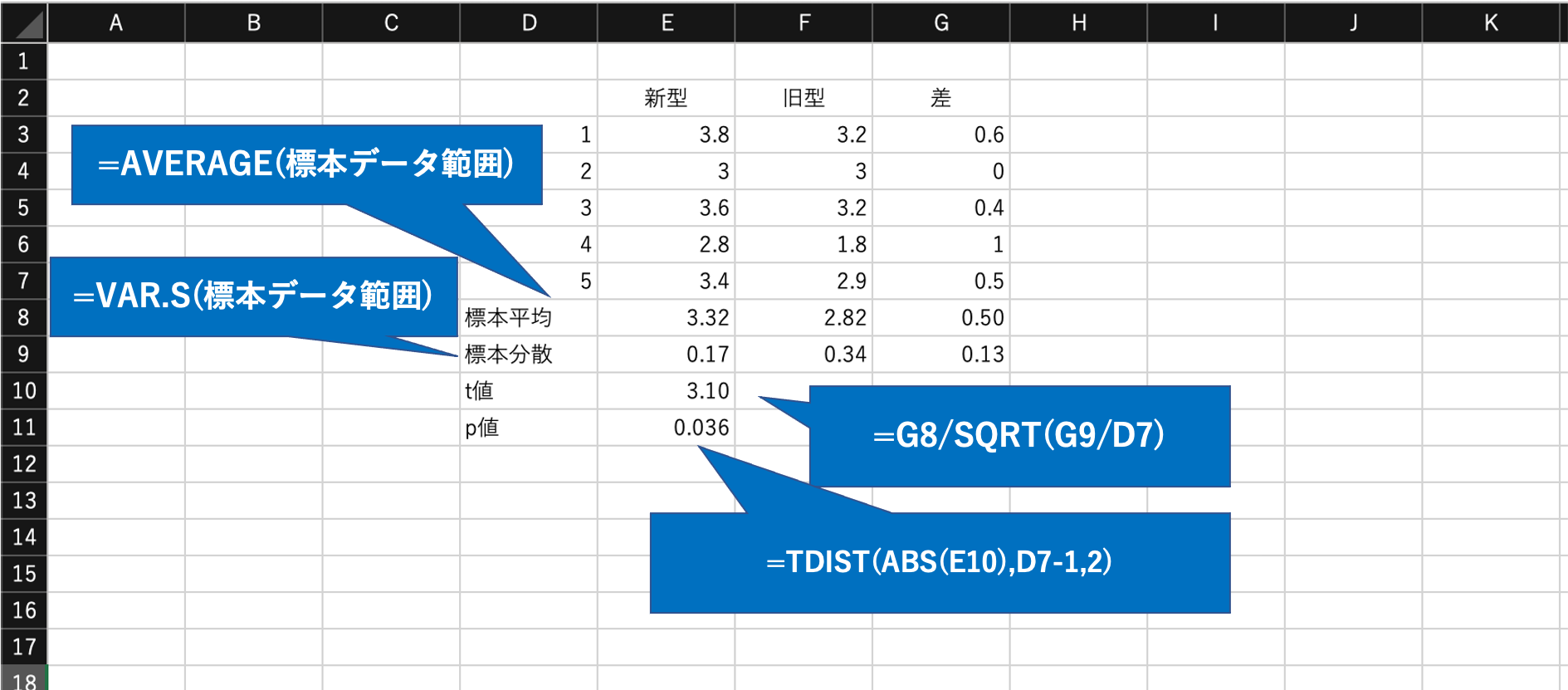
新型と旧型で同時に同サンプルの測定を行い、測定値を下表にまとめました。
| No. | 新型 mg/L | 旧型 mg/L | 差(d) mg/L |
| 1 | 3.8 | 3.2 | 0.6 |
| 2 | 3.0 | 3.0 | 0.0 |
| 3 | 3.6 | 3.2 | 0.4 |
| 4 | 2.8 | 1.8 | 1.0 |
| 5 | 3.4 | 2.9 | 0.5 |
差\(d\)の平均値は、\(\overline{d} = 0.5\)で、差\(d\)の標本分散は、\(s^2=0.13\)でした。
$$s^{2}=\frac{1}{n-1}\sum ^{n}_{i=1}\left( d_{i}-\overline{d}\right) ^{2}$$
同時に同サンプルを測定したため、新型と旧型の測定値には相関があると考えられます。
よって、対応のある2群の「t検定」を行います。
それでは、検定の手順に従って、例題を解いていきましょう。
1.仮説の設定
帰無仮説\(H_0 \):\(\overline{d}=0\)(差\(d\)の母平均は0である)
対立仮説\(H_1 \):\(\overline{d} \neq 0\) (差\(d\)の母平均は0ではない)
プラスでもマイナスでも差があれば、「0ではない」となりますので「両側検定」です。
2.検定統計量の算出
対応のある2群の平均値の検定は、下記の検定統計量tを使用します。
$$\begin{aligned}t&=\frac{\overline{d}}{\sqrt{\frac{s^2}{n}}}\\[5pt]
&=\frac{0.5}{\sqrt{\frac{0.13}{5}}}\\[5pt]
&=3.1\end{aligned}$$
3.棄却域の設定
有意水準は、\(\alpha = 0.05\left( 5\% \right)\)とします。
4.p値の算出
p値はエクセルの関数を使って計算します。
t検定では、TDIST関数に、2.で算出したt値の絶対値を代入して、p値を求めます。
t分布は、自由度に応じて変化しますので、自由度\(n-1\)を指定します。
また、両側検定ですので、定数2も指定します。
エクセル関数
p値 = TDIST(2.で算出したt値の絶対値, 自由度 n - 1 , 両側検定2 )
= TDIST(ABS(3.1), 4, 2)
= 0.036
5.判定
\(p=0.036 < 0.05\)となることから、p値は棄却域に入り、帰無仮説は棄却されます。
6.結論
帰無仮説が棄却されたため、差\(d\)の平均値は0ではないと言えます。
すなわち、新型と旧型のオンライン濃度計では、測定値に有意な差があると言えます。
母分散の差の検定(F検定)
独立な2群の平均値の差の検定(例題④、⑤)では、分散が等しい場合は「t検定」、分散が異なる場合は「Welchの検定」を行いました。
しかし、分散が等しいかどうかの判断についても、平均値と同様に「母分散の差の検定(F検定)」を行う必要があります。
例題④、⑤について母分散の差の検定を行ってみましょう。
【例題⑦】例題④、⑤の母分散の差の検定
(1)例題④の母分散の差の検定
標本分散が\(s_E^2 = 16^2\)、\(s_F^2 = 14^2\)で、データ数は共に10\(( n_{E}=n_{F}= 10)\)です。
(2)例題⑤の母分散の差の検定
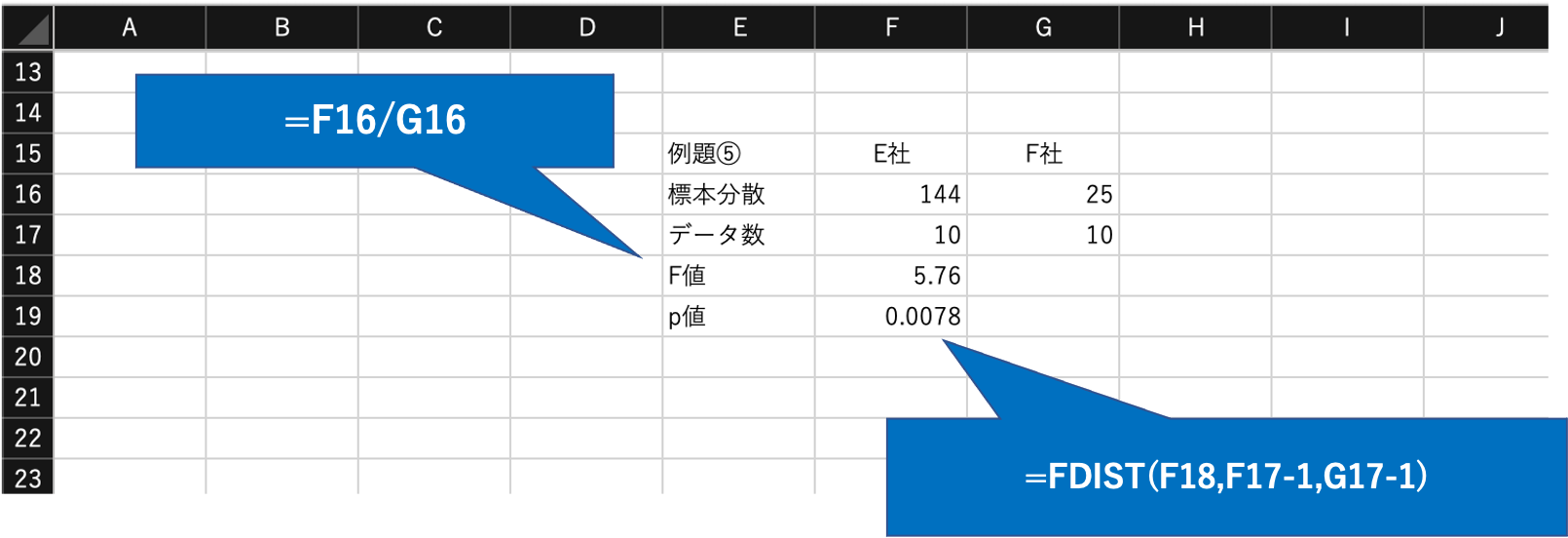
標本分散が\(s_E^2 = 12^2\)、\(s_F^2 = 5^2\)で、データ数は共に10\(( n_{E}=n_{F}= 10)\)です。
それでは、検定の手順に従い検定を行っていきます。
(1)例題④の母分散の差の検定
1.仮説の設定
帰無仮説\(H_0 \):\(\sigma_E^2=\sigma_F^2\) (2つの母分散は等しい)
対立仮説\(H_1 \):\(\sigma_E^2 > \sigma_F^2\) (\(\sigma_E^2\)の方が\(\sigma_F^2\)より大きい)
今回、\(\sigma_E^2\)が、\(\sigma_F^2\)より大きいかどうかを検定するため、「片側検定」とします。
2.検定統計量の算出
母分散の差の検定は、下記の検定統計量\(F\)を使用します。
$$\begin{aligned}F&=\frac{s_E^2}{s_F^2}\\[5pt]
&=\frac{16^2}{14^2}\\[5pt]
&=1.31\end{aligned}$$
※対立仮説\(H_1 \)で大きいと仮定した標本分散\(s_E^2\)を分子に持ってきます。
3.棄却域の設定
有意水準は、\(\alpha = 0.05\left( 5\% \right)\)とします。
4.p値の算出
p値はエクセルの関数を使って計算します。
F検定では、FDIST関数に、2.で算出したF値を代入して、p値を求めます。
F分布は、自由度に応じて変化しますので、分子の自由度(\(n_E -1\))と分母の自由度(\(n_F -1\))を指定します。
エクセル関数
p値 = FDIST(2.で算出したF値, 分子の自由度\(n_E - 1\) ,分母の自由度 \(n_F - 1\) )
= FDIST(1.31, 9, 9)
= 0.35
5.判定
\(p=0.35 > 0.05\)となることから、p値は棄却域に入らず、帰無仮説が採択されます。
6.結論
帰無仮説が採択されたため、母分散に有意な差があるとは言えない。という結論になります。

(2)例題⑤の母分散の差の検定
(1)と同様な手順で検定を行いましょう。
1.仮説の設定
帰無仮説\(H_0 \):\(\sigma_E^2=\sigma_F^2\) (2つの母分散は等しい)
対立仮説\(H_1 \):\(\sigma_E^2 > \sigma_F^2\) (\(\sigma_E^2\)の方が\(\sigma_F^2\)より大きい)
今回、\(\sigma_E^2\)が、\(\sigma_F^2\)より大きいかどうかを検定するため、「片側検定」とします。
2.検定統計量の算出
母分散の差の検定は、下記の検定統計量Fを使用します。
$$\begin{aligned}F&=\frac{s_E^2}{s_F^2}\\[5pt]
&=\frac{12^2}{5^2}\\[5pt]
&=5.76\end{aligned}$$
※対立仮説\(H_1 \)で大きいと仮定した標本分散\(s_E^2\)を分子に持ってきます。
3.棄却域の設定
有意水準は、\(\alpha = 0.05\left( 5\% \right)\)とします。
4.p値の算出
p値はエクセルの関数を使って計算します。
F検定では、FDIST関数に、2.で算出したF値を代入して、p値を求めます。
F分布は、自由度に応じて変化しますので、分子の自由度(\(n_E -1\))と分母の自由度(\(n_F -1\))を指定します。
エクセル関数
p値 = FDIST(2.で算出したF値, 分子の自由度\(n_E - 1\) ,分母の自由度 \(n_F - 1\) )
= FDIST(5.76, 9, 9)
= 0.0078
5.判定
\(p=0.0078 < 0.05\)となることから、p値は棄却域に入り、帰無仮説は棄却されます。
6.結論
帰無仮説が棄却されたため、\(\sigma_E^2\)の方が\(\sigma_F^2\)より大きいと言えます。
すなわち、母分散に有意な差がある(\(\sigma_E^2\)の方が\(\sigma_F^2\)より大きい)と言えます。
無相関検定(t検定)
ようやく最後の例題です。
「相関があるかどうか」の判断についても「t検定」を行うことができます。
それでは、例題を見ていきましょう。
【例題⑧】試作品の製造条件と品質の相関関係
試作品\(G\)の製造条件\(H\)を変更すると、品質\(I\)に大きく影響すると考えられています。
そこで、製造条件\(H\)を様々に変化させて20回(n=20)の試作を行い、品質\(I\)との相関を確認しました。
すると、相関係数\(r =0. 66\)という結果となりました。
この結果から、”中程度の相関がある”ことがわかりますが、これがたまたま(偶然)なのか、本当に相関があるのかを検定をしたいと思います。
それでは、検定の手順に従って、例題を解いていきましょう。
1.仮説の設定
帰無仮説\(H_0 \):\(\rho=0\) (母相関係数が0である)
対立仮説\(H_1 \):\(\rho \neq 0\) (母相関係数が0ではない)
プラスでもマイナスでも差があれば、「0ではない」となりますので「両側検定」です。
2.検定統計量の算出
無相関検定は、下記の検定統計量tを使用します。
$$\begin{aligned}t&=\frac{r}{\sqrt{1-r^{2}}}\times \sqrt{N-2}\\[5pt]
&=\frac{0.66}{\sqrt{1-0.66^{2}}}\times \sqrt{20-2}\\[5pt]
&=3.73\end{aligned}$$
3.棄却域の設定
有意水準は、\(\alpha = 0.05\left( 5\% \right)\)とします。
4.p値の算出
p値はエクセルの関数を使って計算します。
t検定では、TDIST関数に、2.で算出したt値の絶対値を代入して、p値を求めます。
t分布は、自由度に応じて変化しますので、自由度\(n-2\)を指定します。
また、両側検定ですので、定数2も指定します。
エクセル関数
p値 = TDIST(2.で算出したt値の絶対値, 自由度 n - 2 , 両側検定2 )
= TDIST(ABS(3.73), 18, 2)
= 0.0015
5.判定
\(p=0.0015 < 0.05\)となることから、p値は棄却域に入り、帰無仮説は棄却されます。
6.結論
帰無仮説が棄却されたため、母相関係数は0ではないと言えます。
すなわち、相関係数は有意であると言えます。

参考文献
1.心理統計学の基礎(有斐閣アルマ)統計検定2級〜準1級レベル
本記事では、この本を大いに参考にさせてもらいました。
初級から中級レベルに運んでくれるような、非常に詳しい解説があります。
特に「検定力分析によるサンプルサイズの決定」、「線形モデルの基礎」の解説が好きです。
入門書(基本統計学(第3版)など)を読んだ後に、ぜひ挑戦してみて下さい。
統計検定2級を受験する際に、最もお世話になった本です。
非常にわかりやすく書かれています。特に、レイアウトが秀逸で読みやすいのが良いです。
3. Excelで学ぶ統計解析入門-Excel2019/2016対応版
例題を作成する上で参考にしました。
コメントもお待ちしております!!


