どうも。こんにちは。
ケミカルエンジニアのこーしです。
本日は、「正規確率プロット(正規QQプロット)の作成方法」についてわかりやすく解説します。
得られたデータ分布が正規分布に従うかどうかを視覚的に評価できる方法として、「正規確率プロット(正規QQプロット)」があります。
本記事では、正規確率プロットの作成方法と様々な分布の正規確率プロットの特徴を解説します。
正規確率プロットをマスターし、データ分析の信頼性を高めましょう!
本記事の内容
・正規確率プロット(正規QQプロット)とは
・様々な分布の正規確率プロット
・プロセスデータの正規確率プロット
・参考文献
この記事を書いた人

こーし(@mimikousi)
目次
正規確率プロットとは
正規確率プロットは、データが正規分布に従っているかどうかを視覚的に判断するための手法です。
具体的には、サンプルデータと正規分布に従う場合の理論値を比較して、グラフ上にプロットし直線上に乗るかどうかを確認します。
正規確率プロットを描く手順は下記の通りです。
- サンプルデータを小さい順に並べ替える(ソート)する。
- サンプルデータの累積分布関数 (CDF) の値(そのデータより小さいデータの割合)を計算する。
- 2.で計算された累積分布関数 (CDF) の値に対応する標準正規分布の理論値を計算する。
- サンプルデータ(縦軸)と理論値(横軸)をプロットする。
それでは、pythonコードを見てみましょう。
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from scipy.stats import probplot, norm
# 平均値5、標準偏差2.4の正規分布データを生成
np.random.seed(0)
data = np.random.normal(loc=5, scale=2.4, size=100)
# データを昇順にソート
sorted_data = np.sort(data)
# 累積分布関数 (CDF) の値(そのデータ点より小さいデータ点の割合)を計算
cdf_values = [(i + 0.5) / len(sorted_data) for i in range(len(sorted_data))]
# 累積分布関数 (CDF) の値に対応する標準正規分布の理論値を計算
z_scores = norm.ppf(cdf_values)
# 正規確率プロットを1次近似
slope, intercept = np.polyfit(z_scores, sorted_data, 1)
z_values_for_line = np.array([np.min(z_scores), np.max(z_scores)])
data_values_for_line = slope * z_values_for_line + intercept
# グラフを作成
plt.figure(figsize=(6, 5))
plt.scatter(z_scores, sorted_data, c='blue')
plt.plot(z_values_for_line, data_values_for_line, 'r-') # 赤い直線
plt.xlabel('Theoretical Quantiles')
plt.ylabel('Ordered Values')
plt.title('Normal Probability Plot (Custom)')
plt.savefig('Normal Probability Plot (Custom).png', facecolor='white', dpi=100)
注意ポイント
cdf_valuesの(i + 0.5)/len(sorted_data)の部分は、順位iのプロッティングポジションと呼ばれています。
他にも、i/(n + 1)や(i - 3/8)/(n + 1/4)などが用いられることがあります。
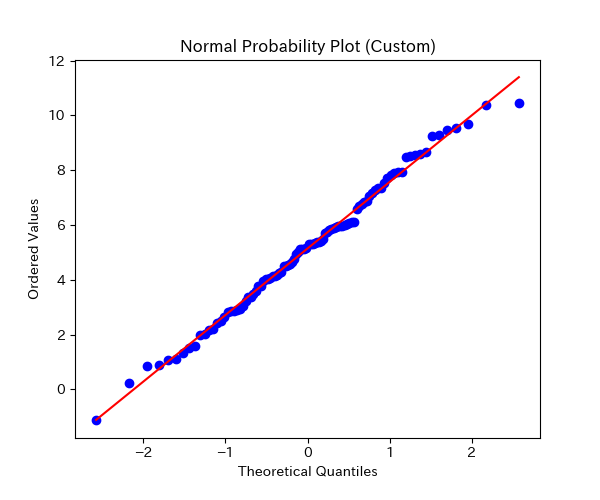
得られたグラフは下図の通りです。
正規分布に従うデータなので、一直線上に乗っていることが確認できます。
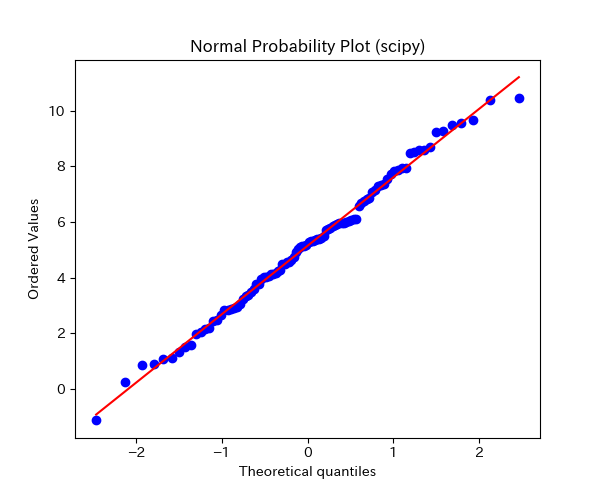
また、scipyライブラリのprobplotを用いると、上記コードがとても簡単になります。
慣れてきたらscipyライブラリを使うと便利ですね。
# scipyのprobplotでプロット
plt.figure(figsize=(6, 5))
probplot(data, dist="norm", plot=plt)
plt.title("Normal Probability Plot (scipy)")
plt.savefig('Normal Probability Plot (scipy).png', facecolor='white', dpi=100)
エクセルで正規確率プロット(正規QQプロット)を描く方法は、下記リンクで詳しく解説されています。
様々な分布の正規確率プロット
正規分布とそれ以外の分布について、正規確率プロットとヒストグラムを確認してみましょう。
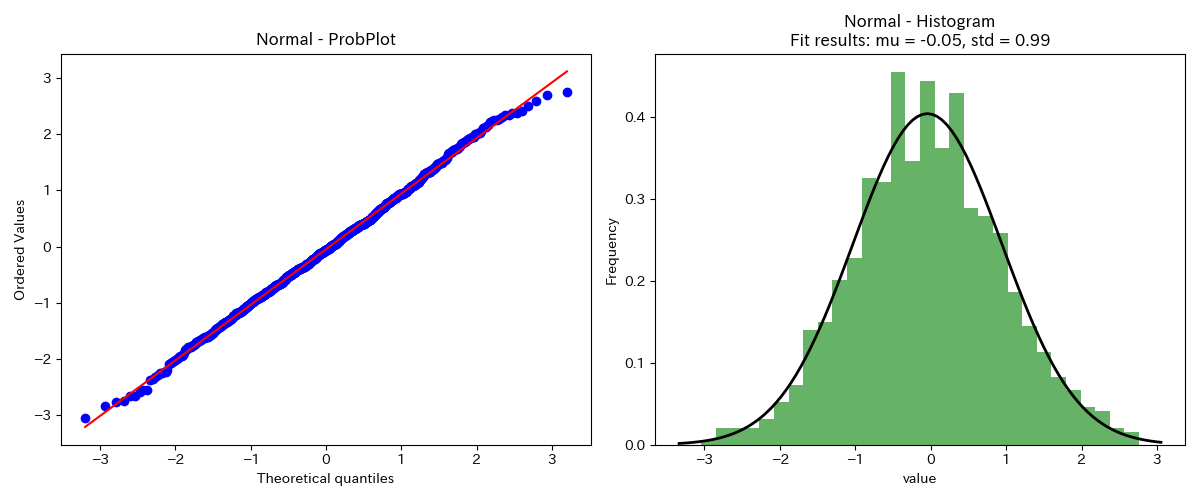
正規分布
正規分布の正規確率プロットは、当然一直線上に乗っていることがわかります。
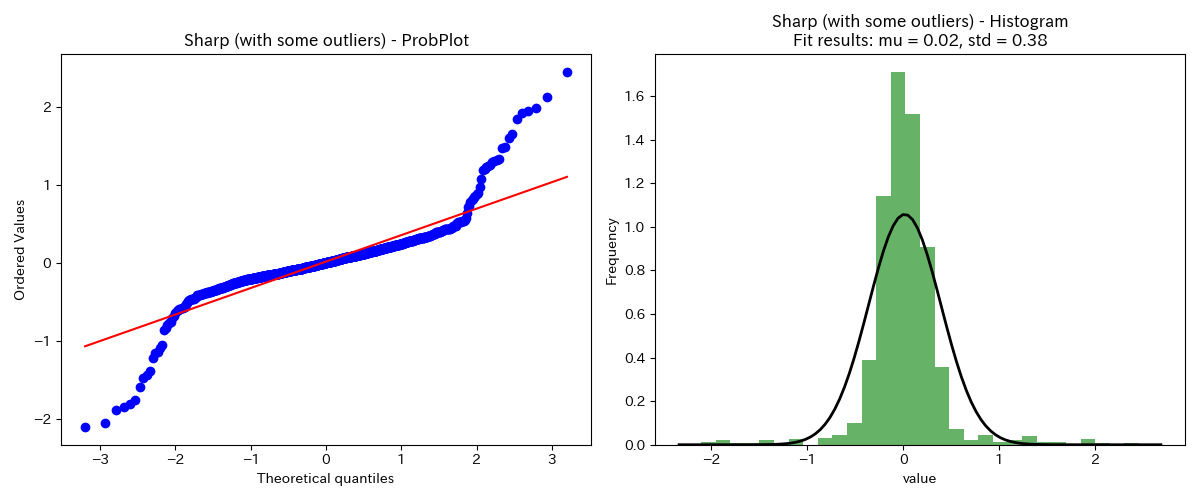
正規分布より裾野が狭い分布
正規確率プロットが、大きい側で直線より上向きになり、小さい側で直線より下向きになっています。
これは、正規分布より裾野が狭くなっていることを表しています。
規格外れのサンプルを取り除いたり、規格内に納まるようにフィードバック制御がかけられている場合に、このような分布になることがあります。
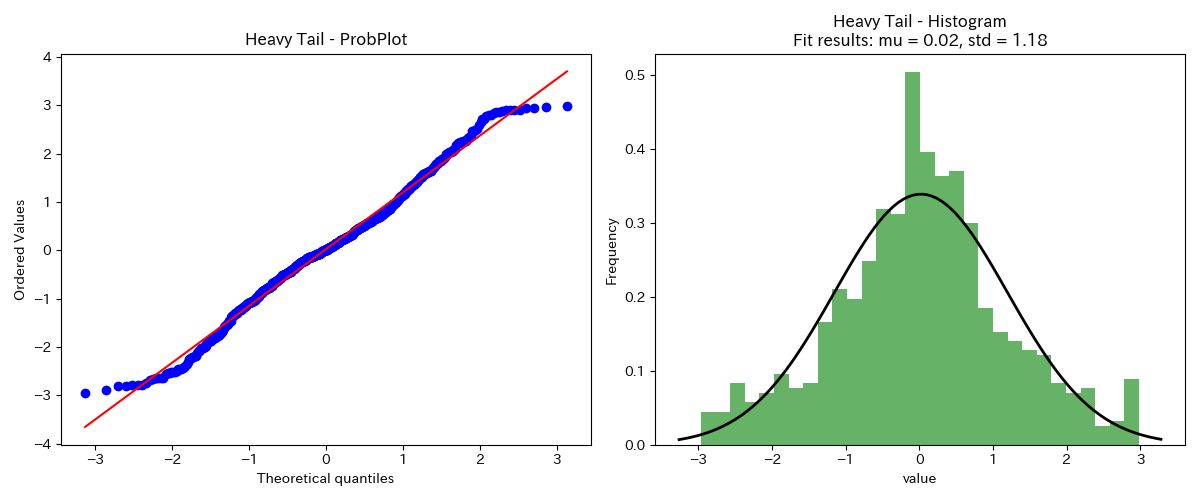
正規分布より裾野が広い分布
正規確率プロットが、大きい側で直線より下向きになり、小さい側で直線より上向きになっています。
これは、正規分布より裾野が広くなっていることを表しています。
下図のデータは、コーシー分布のうち絶対値3以下のデータを抽出したものです。
複雑な系に従う分布では、しばしば裾野が広くなります。
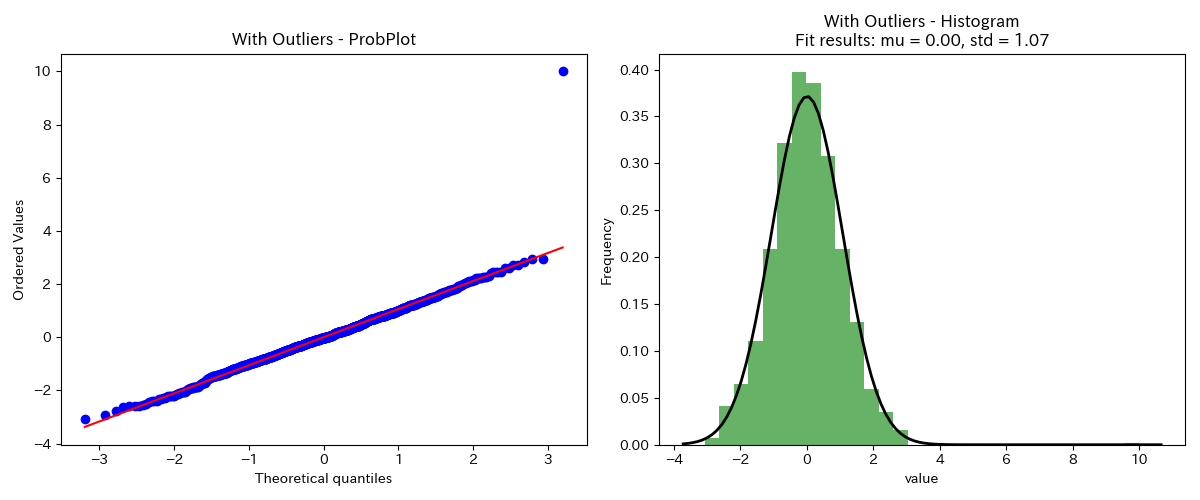
外れ値がある分布
1点だけ不自然にズレている場合、外れ値である可能性が高いです。
正規確率プロットで外れ値の検出もできます。
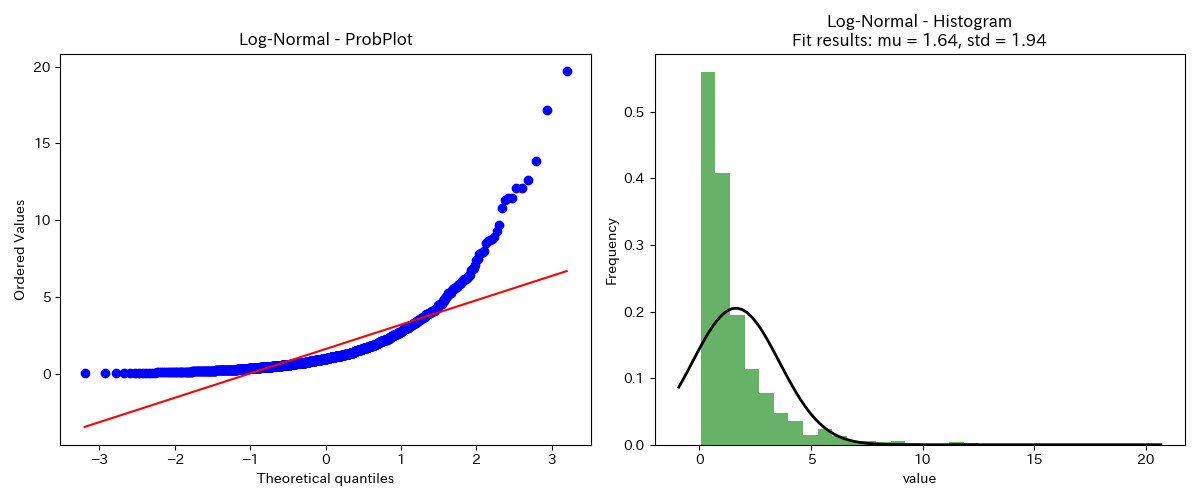
対数正規分布
正規確率プロットが、大きい側で直線より上向きにそり、小さい側でも直線より上向きにそっています。
粒子径分布や分子量分布、微量不純物濃度の分布など、+側に伸びた左右非対称な分布(対数正規分布など)で下図のような挙動となります。
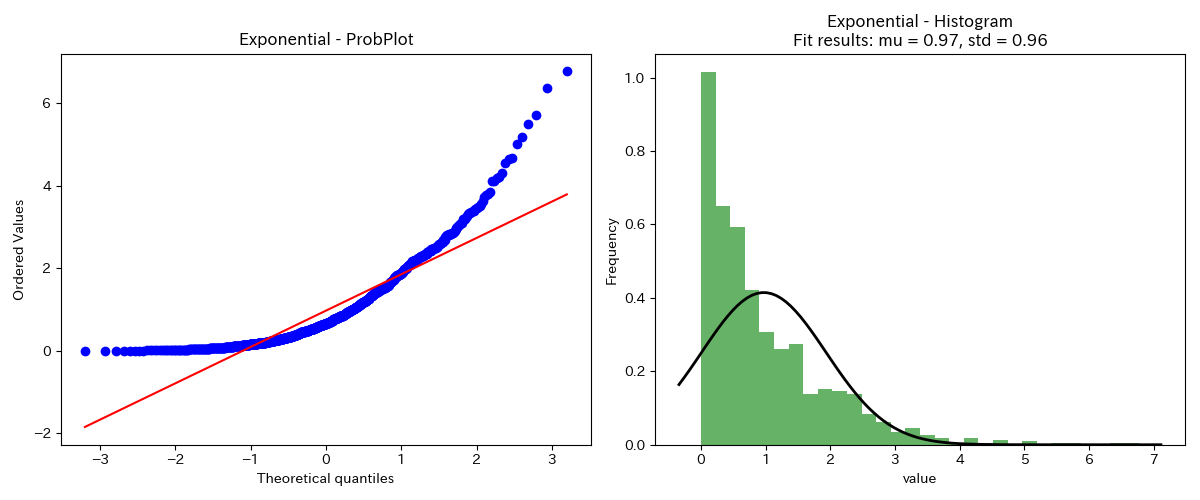
指数分布
対数正規分布と同様に、正規確率プロットが、大きい側で直線より上向きにそり、小さい側でも直線より上向きにそっています。
指数分布は、機器の稼働台数の時間推移などに使われる分布です。
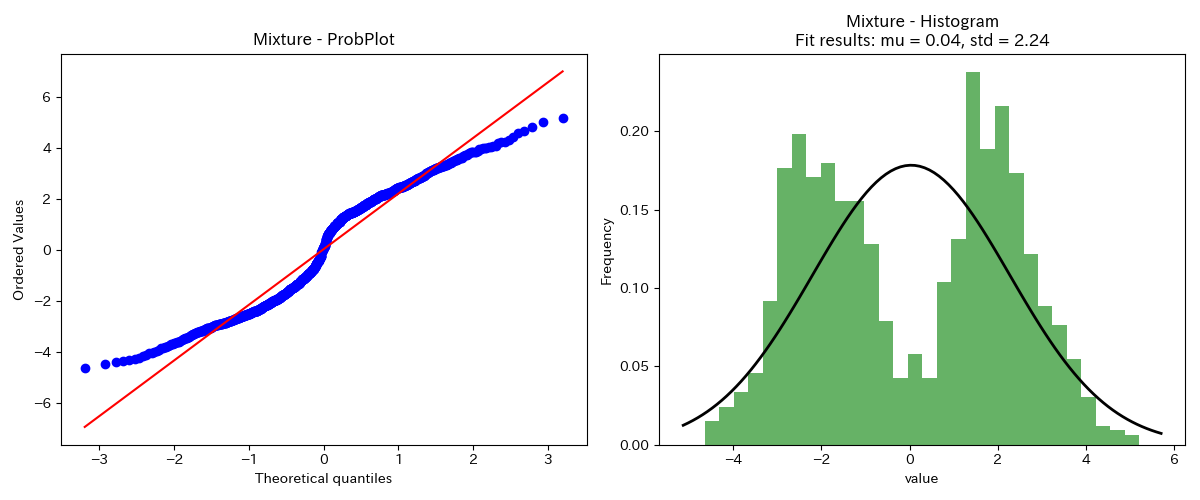
混合分布
二つの正規分布が混ざった混合(正規)分布の正規確率プロットです。
異なる二つの直線が繋がったような形をしています。
温度計や圧力計など、製造プロセスのセンサデータは、正規分布に従うことが多いですが、生産レートを変更したりして異なる運転条件のデータが混ざると、このような混合正規分布になることがあります。
【参考】pythonコード
上記7つのグラフは、下記のコードで作成しています。
アレンジして使ってみてください。
np.random.seed(0)
# データ生成
N = 1000
normal_data = np.random.normal(0, 1, N)
sharp_data = [np.random.normal(0, 0.2) if np.random.rand() > 0.1 else np.random.normal(0, 1) for _ in range(N)]
heavy_tail_data_raw = np.random.standard_cauchy(N)
heavy_tail_data = heavy_tail_data_raw[np.abs(heavy_tail_data_raw) < 3]# 絶対値が3以上のデータを取り除く
outlier_data = np.random.normal(0, 1, N)
outlier_data[500] = 10 # 外れ値を追加
lognormal_data = np.random.lognormal(0, 1, N)
exponential_data = np.random.exponential(1, N)
mixture_data = [np.random.normal(-2, 1) if np.random.rand() > 0.5 else np.random.normal(2, 1) for _ in range(N)]
datasets = [normal_data, sharp_data, heavy_tail_data, outlier_data, lognormal_data, exponential_data, mixture_data]
titles = ['Normal', 'Sharp (with some outliers)', 'Heavy Tail', 'With Outliers', 'Log-Normal', 'Exponential', 'Mixture']
# 各データセットに対するプロット
for i, (data, title) in enumerate(zip(datasets, titles)):
fig, axes = plt.subplots(1, 2, figsize=(12, 5))
# 正規確率プロット
probplot(data, dist="norm", plot=axes[0])
axes[0].set_title(title + ' - ProbPlot')
# ヒストグラム
n, bins, patches = axes[1].hist(data, bins=30, density=True, alpha=0.6, color='g')
mu, std = norm.fit(data)
xmin, xmax = axes[1].get_xlim()
x = np.linspace(xmin, xmax, 100)
p = norm.pdf(x, mu, std)
axes[1].plot(x, p, 'k', linewidth=2)
axes[1].set_xlabel('value')
axes[1].set_ylabel('Frequency')
title_hist = f"{title} - Histogram\nFit results: mu = {mu:.2f}, std = {std:.2f}"
axes[1].set_title(title_hist)
# 保存
plt.tight_layout()
plt.savefig(f"{title.replace(' ', '_').lower()}_qqplot.png", facecolor='white', dpi=100)
plt.show()
ヒストグラムの作成方法については、下記の記事で詳しく解説しています。
bin(縦棒)の数の決め方が重要ですね。
-

-
【python】ヒストグラムの作成方法(スタージェスの公式)
続きを見る
プロセスデータの入手
プロセスデータのサンプルを用いて、ヒストグラムと正規確率プロットを作成してみましょう。
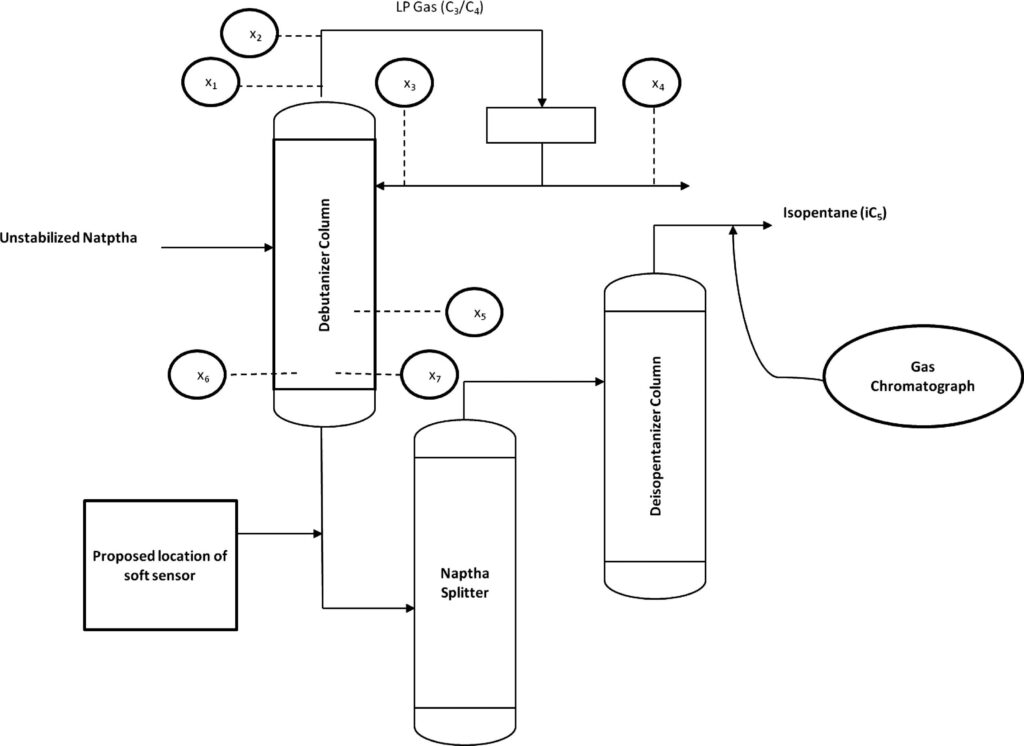
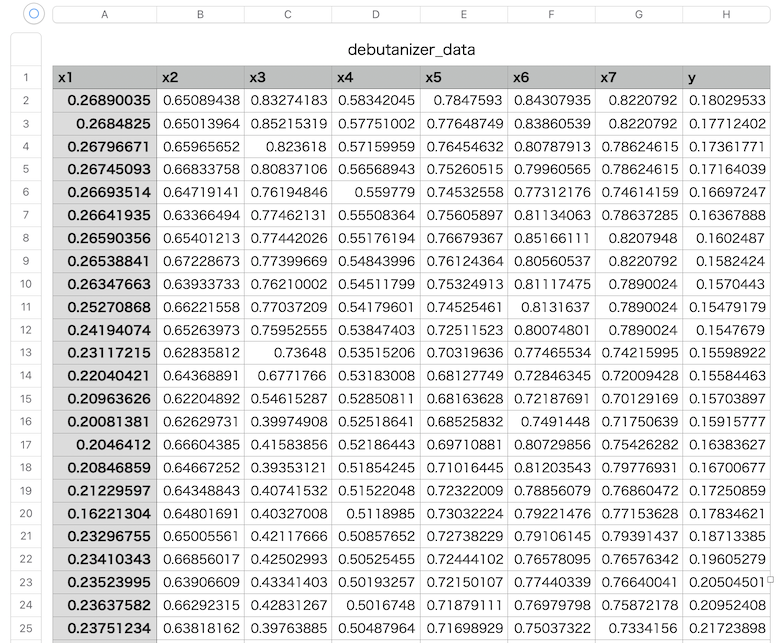
コチラのGitHubページで入手できる「debutanizer_data.csv」を利用します。
脱ブタン塔のプロセスデータであり、プロセスフローは上図の通りです。
説明変数がx1〜x7の7個で、目的変数がyの1個、サンプル数は2394個です。
| 変数名 | 詳細 | 日本語訳 |
|---|---|---|
| x1 | Top Temperature | 塔頂温度 |
| x2 | Top pressure | 塔頂圧力 |
| x3 | Reflux flow | 還流流量 |
| x4 | Flow to next process | 次プロセスへの流量 |
| x5 | 6th tray Temperature | 6段目温度 |
| x6 | Bottom Temperature1 | 塔底温度1 |
| x7 | Bottom Temperature2 | 塔底温度2 |
| y | Butane(C4) content in the debutanizer column bottom | 塔底におけるブタン含有量 |
データの読み込み
「debutanizer_data.csv」と同じフォルダに、「qqplot_debutanizer.ipynb」というファイルを作成しましょう。
下記のコードでライブラリのインポートと、データの読み込みを行います。
import numpy as np
import pandas as pd
from scipy.stats import probplot, norm
import matplotlib.pyplot as plt
from matplotlib.backends.backend_pdf import PdfPages
import japanize_matplotlib
import seaborn as sns
sns.set(font='IPAexGothic')
# ファイルの読み込み
df = pd.read_csv('debutanizer_data.csv')
プロセスデータの正規確率プロット
上記のプロセスデータについて、正規確率プロットを見てみましょう。
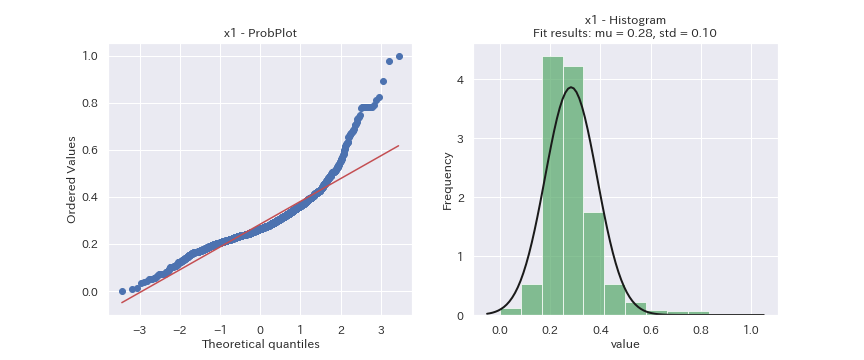
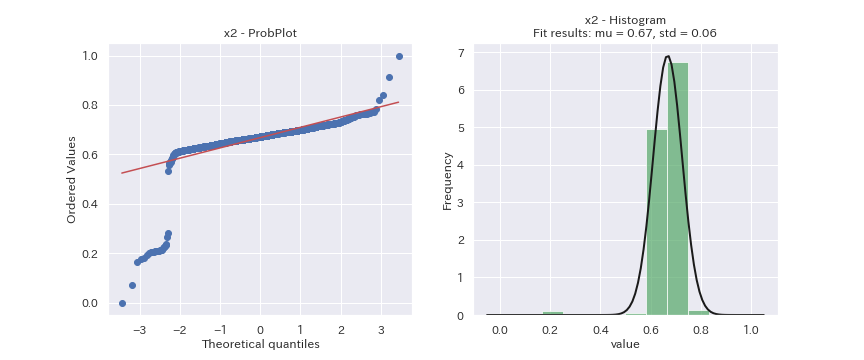
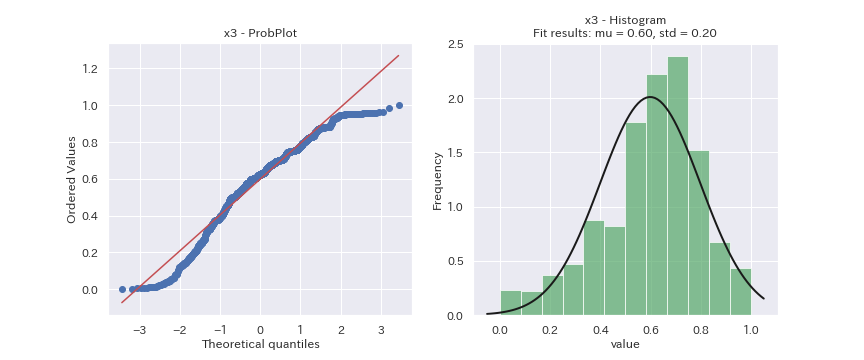
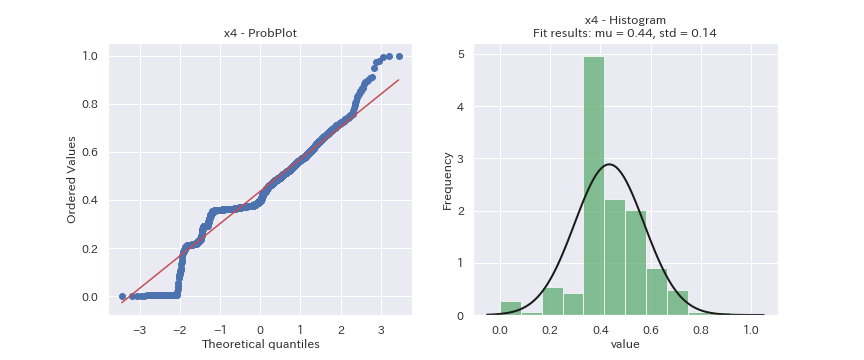
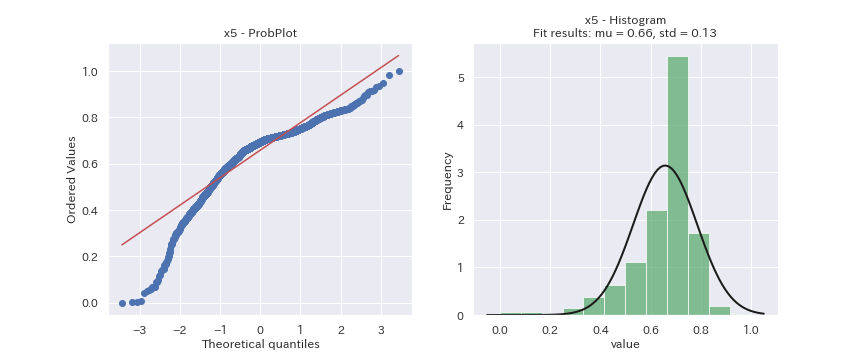
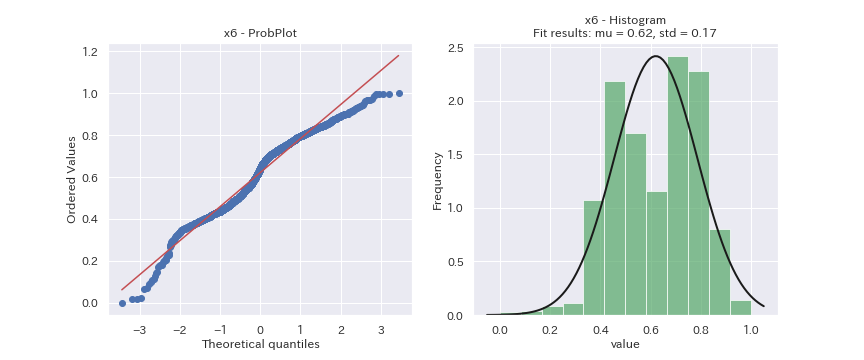
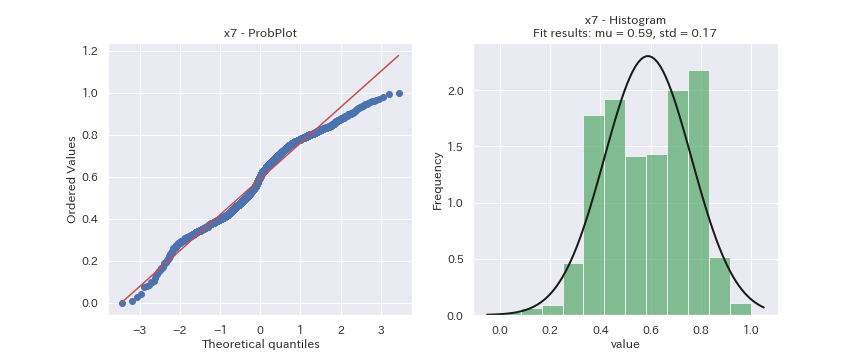
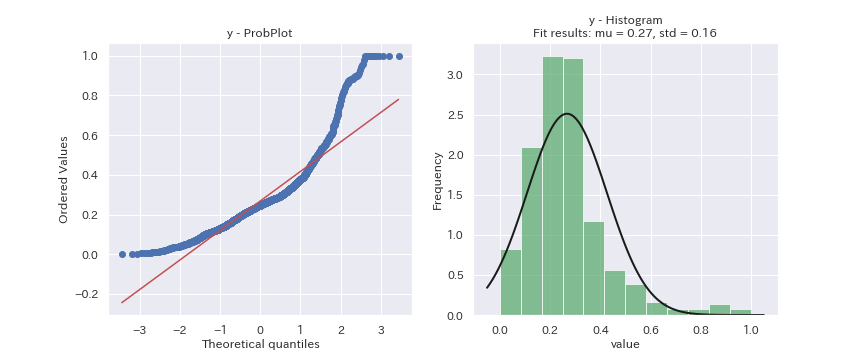
見た目だけの判断になってしまいますが、どの変数も正規分布に従っているデータには見えません。
x2は正規分布より裾野の狭い分布、x3は正規分布より裾野の広い分布、x6とx7は二つの分布の混合分布に見えます。
また、yはブタン含有量であり「微量不純物濃度」と見なせます。
よって、「対数正規分布」に従っている可能性があります。
pythonコード
上記の正規確率プロットとヒストグラムは、下記のコードで作成しました。
画像ファイル(.png)とPDFファイルの両方で保存しています。
#pdfで保存するためpdfインスタンスを作成
pdf = PdfPages('qqplot_debutanizer.pdf')
#Q-Qプロット
for col in df.columns:
df_col = df[col].dropna()
fig, axes =plt.subplots(1, 2, figsize=(12,5))
# 正規確率プロット
probplot(df_col, dist="norm", plot=axes[0])
axes[0].set_title(col + ' - ProbPlot')
# ヒストグラム
# ヒストグラムのbinの数を計算(スタージェスの公式)
num_bins = int(np.log2(df_col.shape[0]) + 1)
# ヒストグラムの表示(density=Trueで密度表示)
axes[1].hist(df_col, bins=num_bins, density=True, alpha=0.7, color='g')
mu, std = norm.fit(df_col)
xmin, xmax = axes[1].get_xlim()
x = np.linspace(xmin, xmax, 100)
p = norm.pdf(x, mu, std)
axes[1].plot(x, p, 'k', linewidth=2)
axes[1].set_xlabel('value')
axes[1].set_ylabel('Frequency')
title_hist = f"{col} - Histogram\nFit results: mu = {mu:.2f}, std = {std:.2f}"
axes[1].set_title(title_hist)
plt.show()
# グラフを保存
pdf.savefig(fig)
fig.savefig(f'{col}_qqplot.png')
plt.close(fig)
#close処理
pdf.close()
まとめ
まとめ
- 正規確率プロットは、データが正規分布に従っているかどうかを視覚的に判断するための手法
- プロットが直線上に乗っていれば「正規分布」に従っている
- 正規確率プロットは、pythonのscipyライブラリ(probplot)を用いて簡単に作成できる
- 正規確率プロットの挙動を詳しく見ることで、データの分布の特徴がわかる
参考文献
本書を主に参考にしました。
化学工学会の学会誌の連載である「ケミカルエンジニアのための統計的品質管理入門」の内容をまとめた教科書です。
化学工学、品質管理に関わる方は一読の価値ありですね。
本記事の関連では、正規分布と異なるときの特徴について詳しく書かれています。
正規確率プロットは、正規性の検定の一種です(本書では正規QQプロットと呼んでいます)。
理論的な裏付けは本書と下記の「自然科学の統計学」を参考にしました。
通称「赤本」と呼ばれる「統計学入門」の続編として書かれた「青本(通称)」です。
赤本とセットで統計検定1級の対策にも使えるほど難易度高めです。
本書では、上述の教科書「正規性の検定」の内容のダブルチェックととして参考にしました。
正規確率プロットの内容はとてもわかりやすく、本書を読んで理解が深まりました

