どうも。こんにちは。
ケミカルエンジニアのこーしです。
本日は、「pythonを用いた単変量の外れ値除去」についてわかりやすく解説します。
データに外れ値があると、不適切な分析結果を出してしまいます。
そこで本記事では、Pythonを用いて外れ値を除去する3つの手法を紹介します。
それぞれの手法がどのように機能するのか、また、いつ使用すべきなのかがわかるようになります。
本記事の内容
・外れ値除去の3つの手法(単変量)
・3シグマ法
・Hampel Identifier
・平滑化前後の差分に対してHampel Identifier
・参考文献
この記事を書いた人

こーし(@mimikousi)
目次
外れ値除去の3つの手法(単変量)
単変量の外れ値除去には、いくつかの手法がありますが、本記事では下記3つの手法を紹介します。
4つの手法
- 3シグマ法
- Hampel Identifier
- 平滑化前後の差分に対してHampel Identifier
上記の手法以外でも、ドメイン知識を駆使して外れ値を除去することも重要です。
また、本記事ではpythonを使用しますが、下記の記事ではエクセルで行う方法を解説しています。
-

-
【エクセルでできる】外れ値の検出方法
続きを見る
サンプルデータの入手
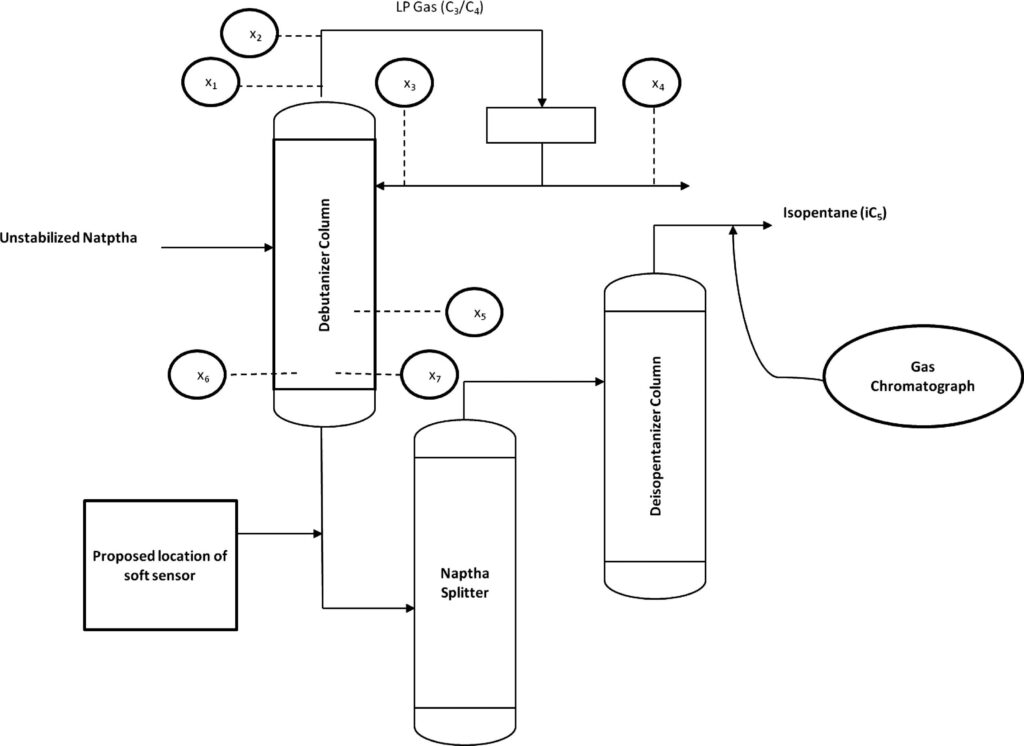
コチラのgithubページで入手できる「debutanizer_data.csv」を利用します。
脱ブタン塔のプロセスデータであり、プロセスフローは上図の通りです。
説明変数がx1〜x7の7個で、目的変数がyの1個、サンプル数は2394個です。
| 変数名 | 詳細 | 日本語訳 |
|---|---|---|
| x1 | Top Temperature | 塔頂温度 |
| x2 | Top pressure | 塔頂圧力 |
| x3 | Reflux flow | 還流流量 |
| x4 | Flow to next process | 次プロセスへの流量 |
| x5 | 6th tray Temperature | 6段目温度 |
| x6 | Bottom Temperature1 | 塔底温度1 |
| x7 | Bottom Temperature2 | 塔底温度2 |
| y | Butane(C4) content in the debutanizer column bottom | 塔底におけるブタン含有量 |
データの読み込み
「debutanizer_data.csv」と同じフォルダに、「outlier_detection.ipynb」というファイルを作成しましょう。
下記のコードでライブラリのインポートと、データの読み込みを行います。
簡単な前処理として、目的変数yの測定時間を考慮し、5行だけずらしておきましょう。
import pandas as pd
import numpy as np
import scipy as sp
from scipy import signal
import matplotlib.pyplot as plt
import japanize_matplotlib
import seaborn as sns
sns.set(font='IPAexGothic')
from matplotlib.backends.backend_pdf import PdfPages #pdfで保存する
# ファイルの読み込み
df = pd.read_csv('debutanizer_data.csv')
# 目的変数の測定誤差を考慮
df['y'] = df['y'].shift(5)
#yがnanとなる期間のデータを削除
df = df.dropna()
#インデックスをリセット
df = df.reset_index(drop=True)
pythonによる外れ値除去
1.3シグマ法
一般的によく使われる3シグマ法で外れ値を除去してみましょう。
pythonコードは下記の通りです。
#3シグマ法 df_3sigma = df[abs(df - df.mean()) < 3 * df.std()] df_outliers_3sigma = df[abs(df - df.mean()) > 3 * df.std()]
各列の平均から3σ以内にあるデータを取り出し、新しいデータフレームdf_3sigmaを作成しています。
さらに、平均から3σを超えるデータ(つまり、外れ値)も取り出し、新しいデータフレームdf_outliers_3sigmaを作成しています。
実際にどのように外れ値が除去されているのか、可視化してみましょう!
# 3シグマ法
# データフレームdfから上限制御線(UCL)と下限制御線(LCL)を計算します。
# UCLは平均値プラス3倍の標準偏差で、LCLは平均値マイナス3倍の標準偏差で計算されます。
ucl = df.mean() + 3 * df.std()
lcl = df.mean() - 3 * df.std()
# 次に、データフレームdf内のすべての値がUCLとLCLの間にあるデータ(外れ値を除去したデータ)を選択します。
df_3sigma = df[(df > lcl) & (df < ucl)]
# UCLまたはLCLを超える値(外れ値)も選択します。
df_outliers_3sigma = df[(df > ucl) | (df < lcl)]
# PdfPagesを使ってグラフをPDFに保存します。
pdf = PdfPages('debutanizer_3sigma.pdf')
# df内の各列に対して、次の処理を行います。
for col in df.columns:
# 外れ値の数を数えます。
outliers_number = df_outliers_3sigma[col].notna().sum()
# matplotlibを使ってデータをプロットします。
fig, ax = plt.subplots(figsize=(10,5))
# 元のデータを青色の線でプロットします。
ax.plot(df_3sigma[col], label='data')
# 外れ値を赤色の点でプロットします。
ax.scatter(df_outliers_3sigma.index, df_outliers_3sigma[col], c='red', label=f'outliers={outliers_number}')
# UCLとLCLを橙色の線でプロットします。今回はデータの最小と最大インデックスに合わせてx軸を調整します。
ax.plot([df_3sigma[col].index.min(), df_3sigma[col].index.max()], [ucl[col], ucl[col]], c='orange', label='ucl')
ax.plot([df_3sigma[col].index.min(), df_3sigma[col].index.max()], [lcl[col], lcl[col]], c='orange', label='lcl')
# Y軸のラベルを設定します。
ax.set_ylabel(col)
# 凡例をプロットします。
ax.legend(loc='best')
# タイトルを設定します
ax.set_title(f'3 Sigma Method for {col}')
# グラフをPNG画像として保存します。ファイル名は現在の列名に依存します。
fig.savefig(f'{col}_3sigma.png', dpi=150)
# グラフをPDFとして保存します。
pdf.savefig(fig)
# グラフを表示します。
plt.show()
# メモリを節約するために、作成したグラフを閉じます。
plt.close(fig)
# すべてのグラフを描画し終えたら、PDFを閉じて保存します。
pdf.close()
代表として、'x1'と'x2'、'x7'の3つのグラフを見てみましょう。
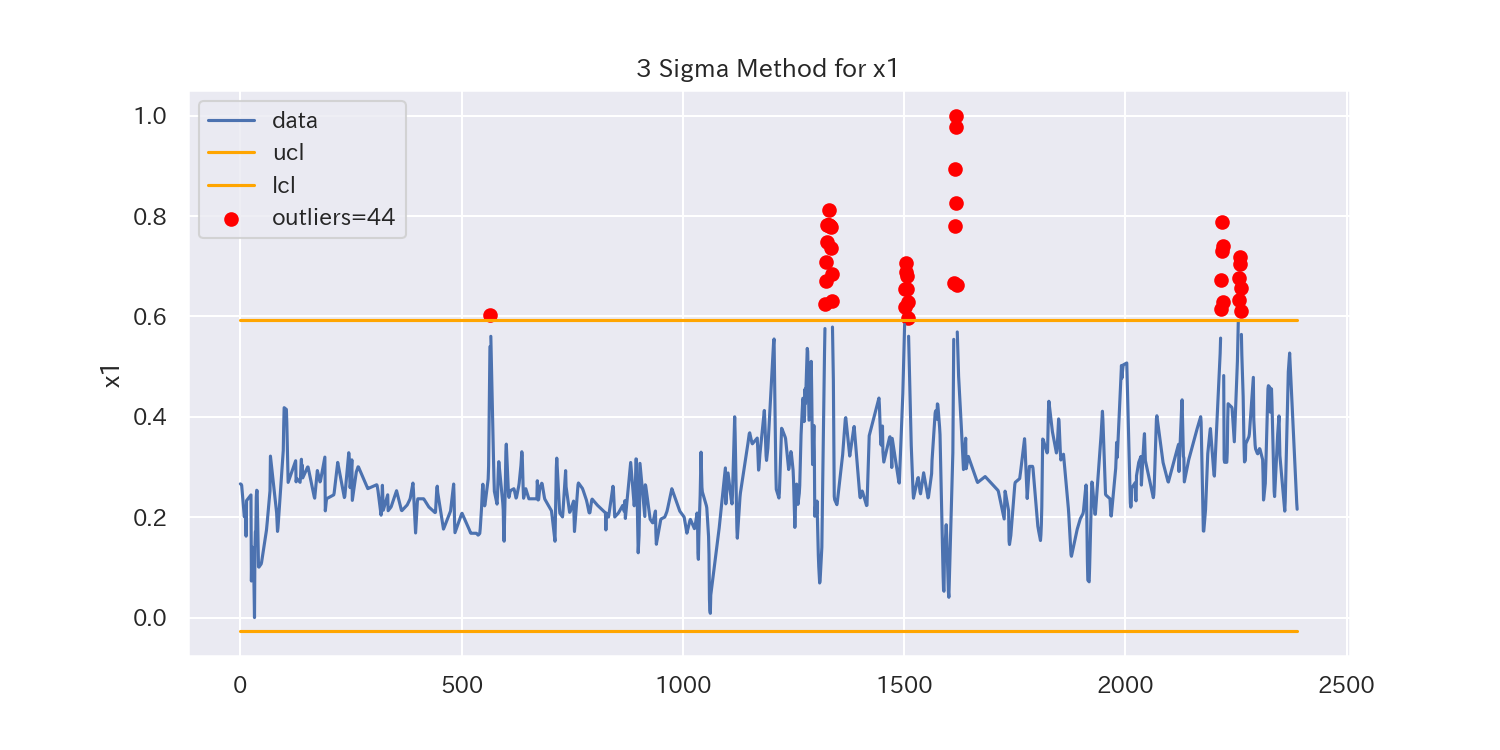
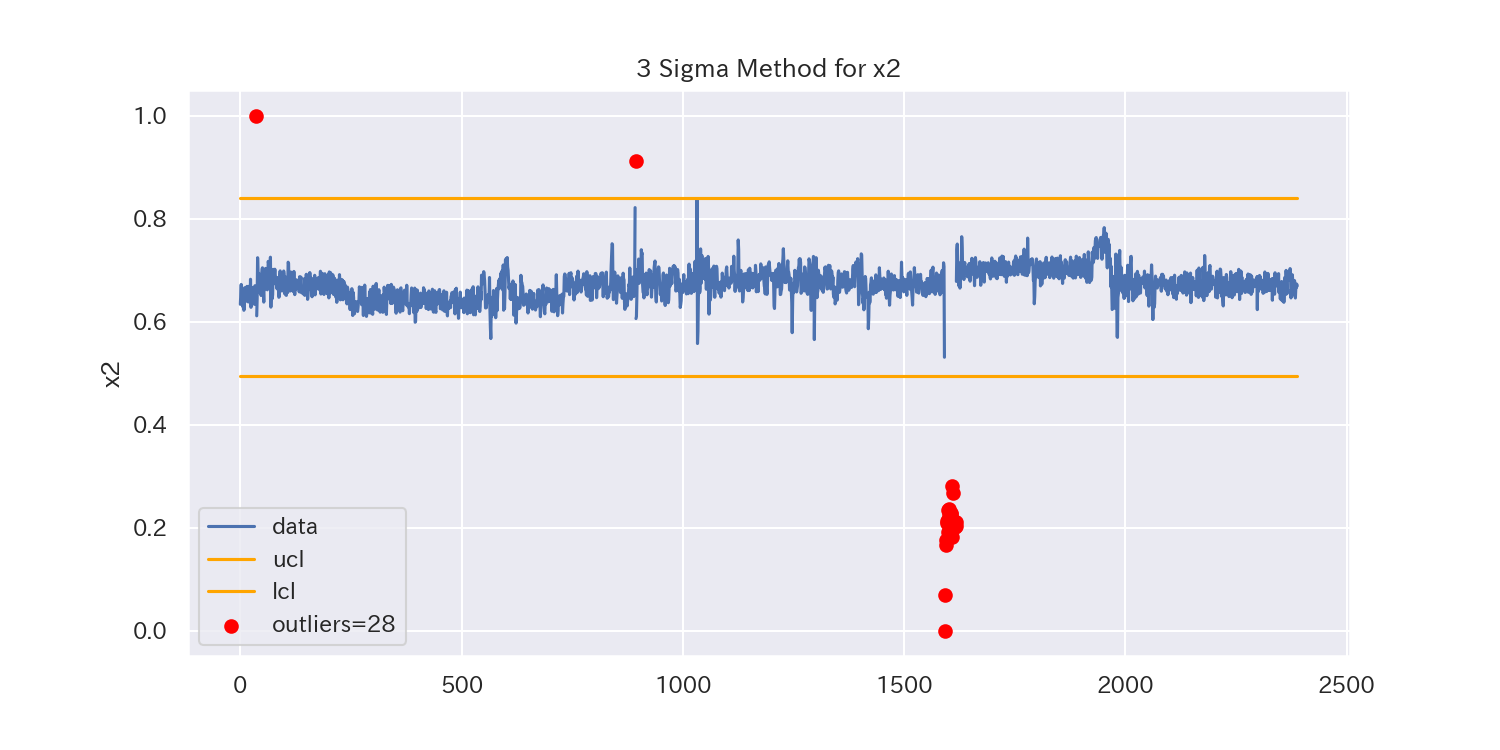
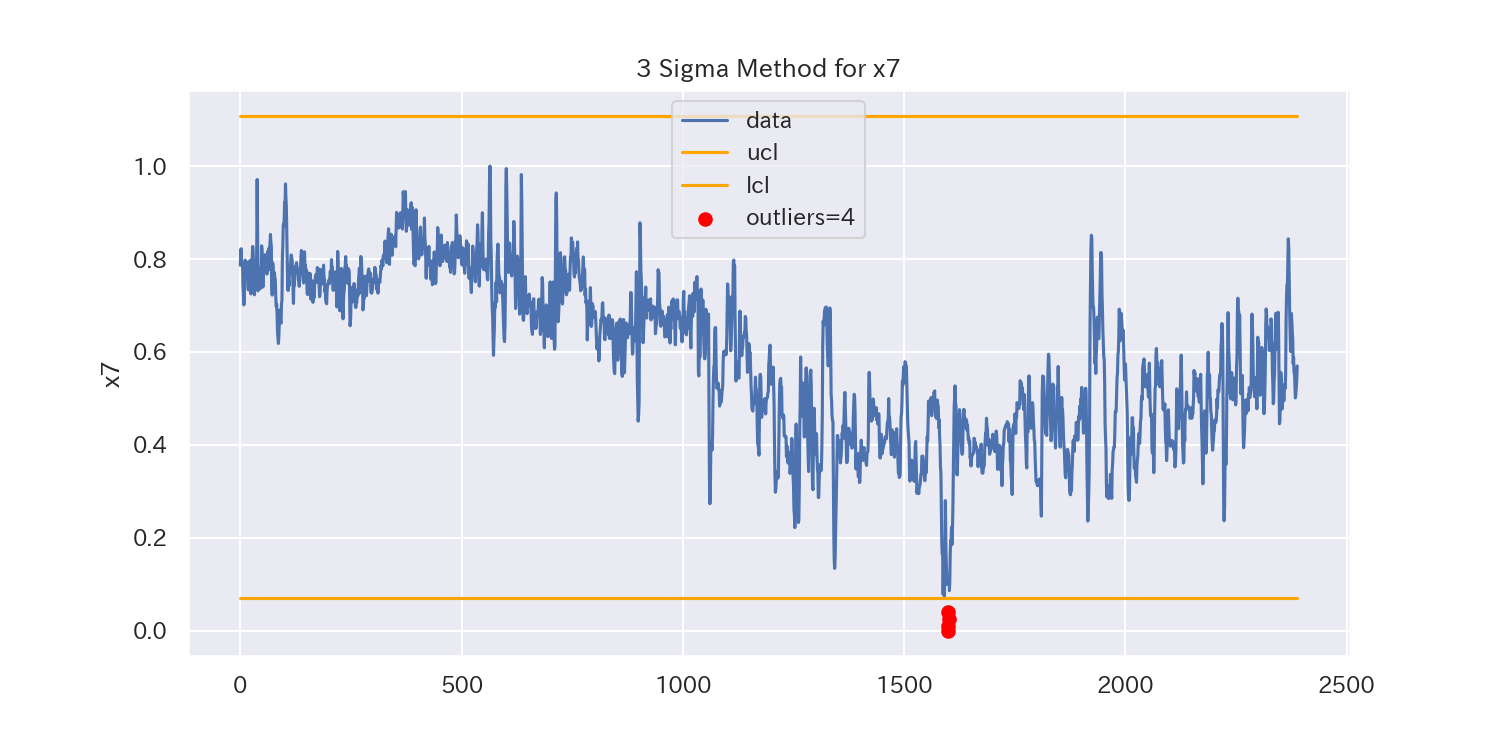
うまく外れ値を除去できているように見えますが、一部除去できていない外れ値もありそうです。
2.Hampel Identifier
Hampel Identifierでは、中央値と中央絶対偏差(MAD :Median Absolute Deviation )を使用して外れ値を検出します。
3シグマ法では「平均値」と「標準偏差」を用いるため、外れ値によって平均値がズレたり、標準偏差が大きくなったりして、閾値に影響を与えてしまうことがありますが、Hampel Identifierではその点を考慮し、中央値とMADを用います。
よって、3シグマ法と比べると、Hampel Identifierは外れ値に対してロバスト(頑健)な手法と言えます。
# Hampel Identifier # データフレームdfの各値がその列の中央値からどの程度離れているかを計算します。 diff = abs(df - df.median()) # MADを計算します。 mad = 1.4826 * diff.median() # 中央値から3 * MADを超える値(外れ値)を除去し、新しいデータフレームdf_hampel_を作成します。 df_hampel = df[abs(df - df.median()) < 3 * mad] # 中央値から3 * MADを超える値(外れ値)だけを取り出し、新しいデータフレームdf_outliers_hampel_を作成します。 df_outliers_hampel = df[abs(df - df.median()) > 3 * mad]
上記のコードはHampel Identifierを用いて、各列の中央値から3 * MAD以内にあるデータを取り出します。
さらに、中央値から3 * MADを超えるデータ(つまり、外れ値)も取り出します。
注意ポイント
正規分布に従う場合、MADと標準偏差が一致するように1.4826を掛けています。
実際にどのように外れ値が除去されているのか、可視化してみましょう!
# Hampel Identifier
diff = abs(df - df.median())
mad = 1.4826*diff.median()
# データフレームdfから上限制御線(UCL)と下限制御線(LCL)を計算します。
ucl = df.median() + 3 * mad
lcl = df.median() - 3 * mad
# 次に、データフレームdf内のすべての値がUCLとLCLの間にあるデータ(外れ値を除去したデータ)を選択します。
df_hampel = df[(df > lcl) & (df < ucl)]
# UCLまたはLCLを超える値(外れ値)も選択します。
df_outliers_hampel = df[(df > ucl) | (df < lcl)]
# PdfPagesを使ってグラフをPDFに保存します。
pdf = PdfPages('debutanizer_hampel.pdf')
# df内の各列に対して、次の処理を行います。
for col in df.columns:
# 外れ値の数を数えます。
outliers_number = df_outliers_hampel[col].notna().sum()
# matplotlibを使ってデータをプロットします。
fig, ax = plt.subplots(figsize=(10,5))
# 元のデータを青色の線でプロットします。
ax.plot(df_hampel[col], label='data')
# 外れ値を赤色の点でプロットします。
ax.scatter(df_outliers_hampel.index, df_outliers_hampel[col], c='red', label=f'outliers={outliers_number}')
# UCLとLCLを橙色の線でプロットします。今回はデータの最小と最大インデックスに合わせてx軸を調整します。
ax.plot([df_hampel[col].index.min(), df_hampel[col].index.max()], [ucl[col], ucl[col]], c='orange', label='ucl')
ax.plot([df_hampel[col].index.min(), df_hampel[col].index.max()], [lcl[col], lcl[col]], c='orange', label='lcl')
# Y軸のラベルを設定します。
ax.set_ylabel(col)
# 凡例をプロットします。
ax.legend(loc='best')
# タイトルを設定します
ax.set_title(f'Hampel Identifier for {col}')
# グラフをPNG画像として保存します。ファイル名は現在の列名に依存します。
fig.savefig(f'{col}_hampel.png', dpi=150)
# グラフをPDFとして保存します。
pdf.savefig(fig)
# グラフを表示します。
plt.show()
# メモリを節約するために、作成したグラフを閉じます。
plt.close(fig)
# すべてのグラフを描画し終えたら、PDFを閉じて保存します。
pdf.close()
代表として、'x1'と'x2'、'x7'の3つのグラフを見てみましょう。
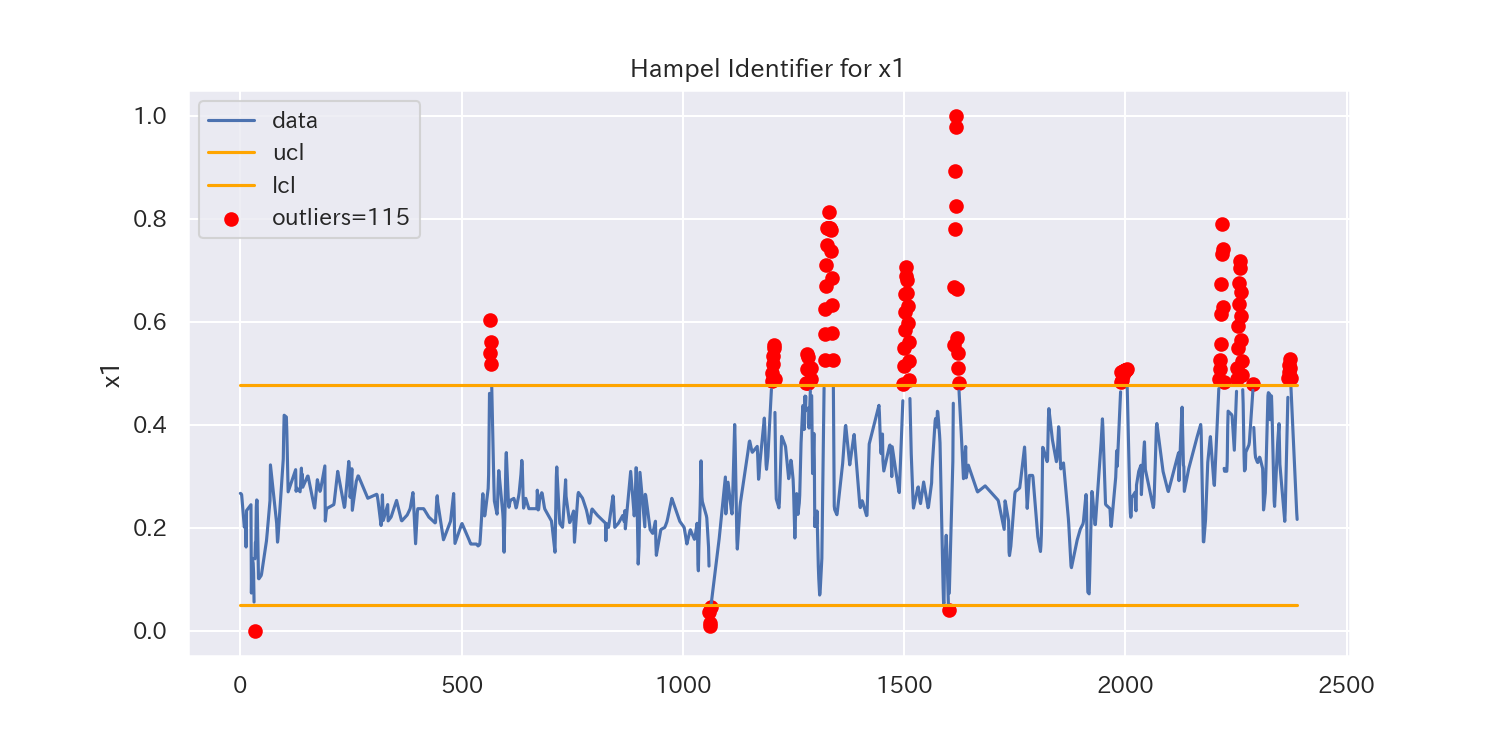
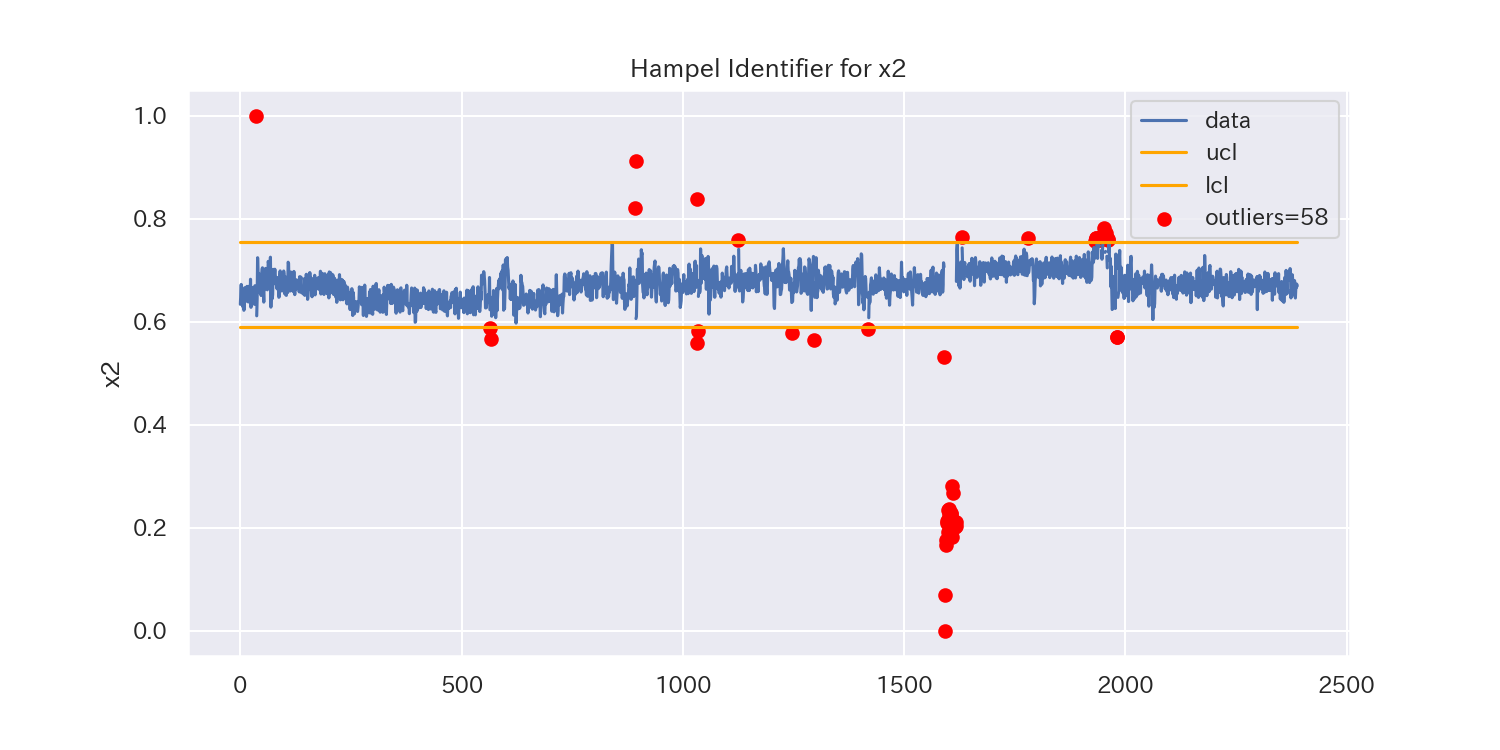
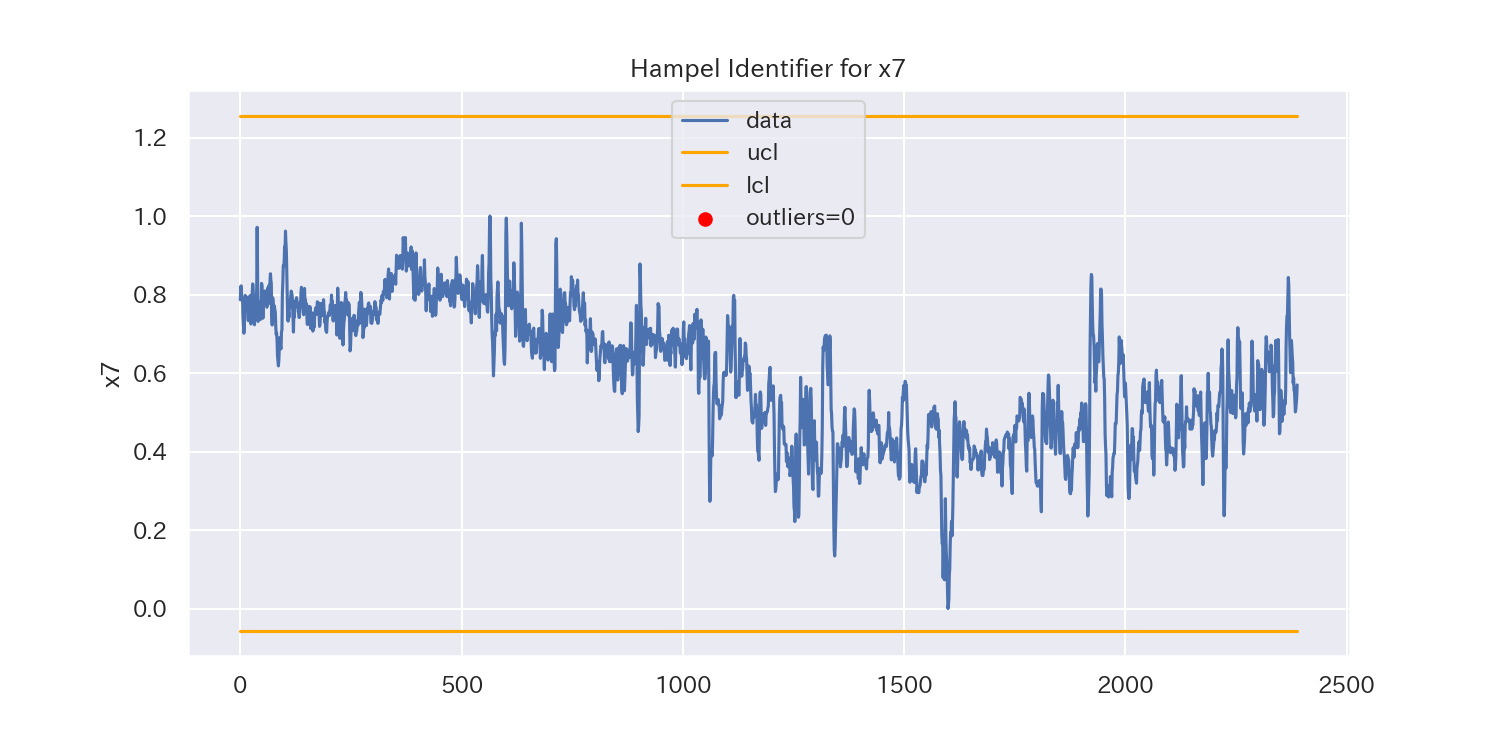
3シグマ法に比べて、外れ値に頑健(ロバスト)であるため、検出できる外れ値がかなり増加しています。
一方、'x7'のようにトレンドのあるデータでは外れ値が検出しにくくなっています。
3.平滑化前後の差分に対してHampel Identifier
プロセスデータのような時系列データでは、平滑化による外れ値除去が用いられます。
なぜなら、時系列データではトレンド(変数の時間変化)をもつため、データセット全体に対する閾値では対応しきれないことが多いからです。
よって、平滑化前後の差分が大きい値を外れ値と見なして除去します。
データの平滑化(savgol_filter)
平滑化手法として、本記事ではSavitzky-Goley法を用います。
Savitzky-Goley法は、Scipyライブラリのsavgol_filterで簡単に実装できますが、平滑化パラメータ(window_length、polyorder)を事前に設定する必要があります。
window_length:窓枠の数(奇数のみ)
polyorder:多項式の次数(window_lenghtより小さくする)
savgol_filterの使い方や、パラメータの決定方法については下記の記事で詳しく解説しています。
-

-
【python】プロセスデータ の平滑化(savgol_filter)
続きを見る
本記事では、平滑化パラメータを手動で試行錯誤できるようにしました。
# 各列に対する'best_window_length'と'best_polyorder'の値 window_length = [71, 71, 71, 71, 71, 71, 71, 71] polyorder = [1, 1, 1, 1, 1, 1, 1, 1] # パラメータDataFrameの作成 df_param = pd.DataFrame(index=['best_window_length', 'best_polyorder'], columns=df.columns) df_param.loc['best_window_length', :] = window_length df_param.loc['best_polyorder', :] = polyorder
続いて、savgol_filterで平滑化を行います。
# 平滑化されたデータ用の空のDataFrameを作成
df_sg = pd.DataFrame(index=df.index)
# 各列データを平滑化して、結果をdf_sgに格納
for col in df.columns:
df_sg[col] = signal.savgol_filter(df[col], window_length=df_param.loc['best_window_length', col], polyorder=df_param.loc['best_polyorder', col])
平滑化前後の差分に対して、Hampel Identifierを適用します。
# 平滑化前後の差分
delta_df = abs(df - df_sg)
# Hampel Identifierの適用
delta_diff = abs(delta_df - delta_df.median())
mad = 1.4826 * delta_diff.median()
cl = delta_df.median() + 3 * mad
delta_new = delta_df[delta_diff < 3 * mad]
delta_outliers = delta_df[delta_diff > 3 * mad]
# 新しいデータフレームを作成して平滑化データと外れ値を格納
df_sg_hampel = pd.DataFrame(index=delta_new.index)
df_outliers_sg_hampel = pd.DataFrame(index=delta_outliers.index)
for col in delta_new.columns:
df_index = delta_new[col].dropna().index
outlier_index = delta_outliers[col].dropna().index
df_sg_hampel[col] = df[col].loc[df_index]
df_outliers_sg_hampel[col] = df[col].loc[outlier_index]
実際にどのように外れ値が除去できているのか、可視化してみましょう!
# PDFの保存先を設定します。
pdf = PdfPages('debutanizer_sg_hampel.pdf')
# 各列のデータに対してプロットと分析を行います。
for col in df.columns:
# 外れ値の数を計算します。
outliers_number = df_outliers_sg_hampel[col].notna().sum()
# グラフの設定
fig, ax = plt.subplots(figsize=(10,5))
# 元のデータをプロット
ax.plot(df_sg_hampel[col], alpha=0.7, label='data')
# 平滑化データをプロット
ax.plot(df_sg[col], c='green', label='savgol_filter')
# 外れ値を赤色でプロット
ax.scatter(df_outliers_sg_hampel.index, df_outliers_sg_hampel[col], c='red', label=f'outliers={outliers_number}')
# UCLとLCLを橙色でプロット
ax.plot(df_sg[col].index, df_sg[col] + cl[col], c='orange', label='ucl')
ax.plot(df_sg[col].index, df_sg[col] - cl[col], c='orange', label='lcl')
# Y軸のラベル、凡例、タイトルの設定
ax.set_ylabel(col)
ax.legend(loc='best')
ax.set_title(f'Smoothing Hampel Identifier for {col}')
# PNGとして保存
fig.savefig(f'{col}_sg_hampel.png', dpi=150)
# PDFに追加
pdf.savefig(fig)
# グラフの表示
plt.show()
# グラフの閉じる(メモリ節約)
plt.close(fig)
# PDFを閉じて保存
pdf.close()
代表として、'x1'と'x2'、'x7'の3つのグラフを見てみましょう。
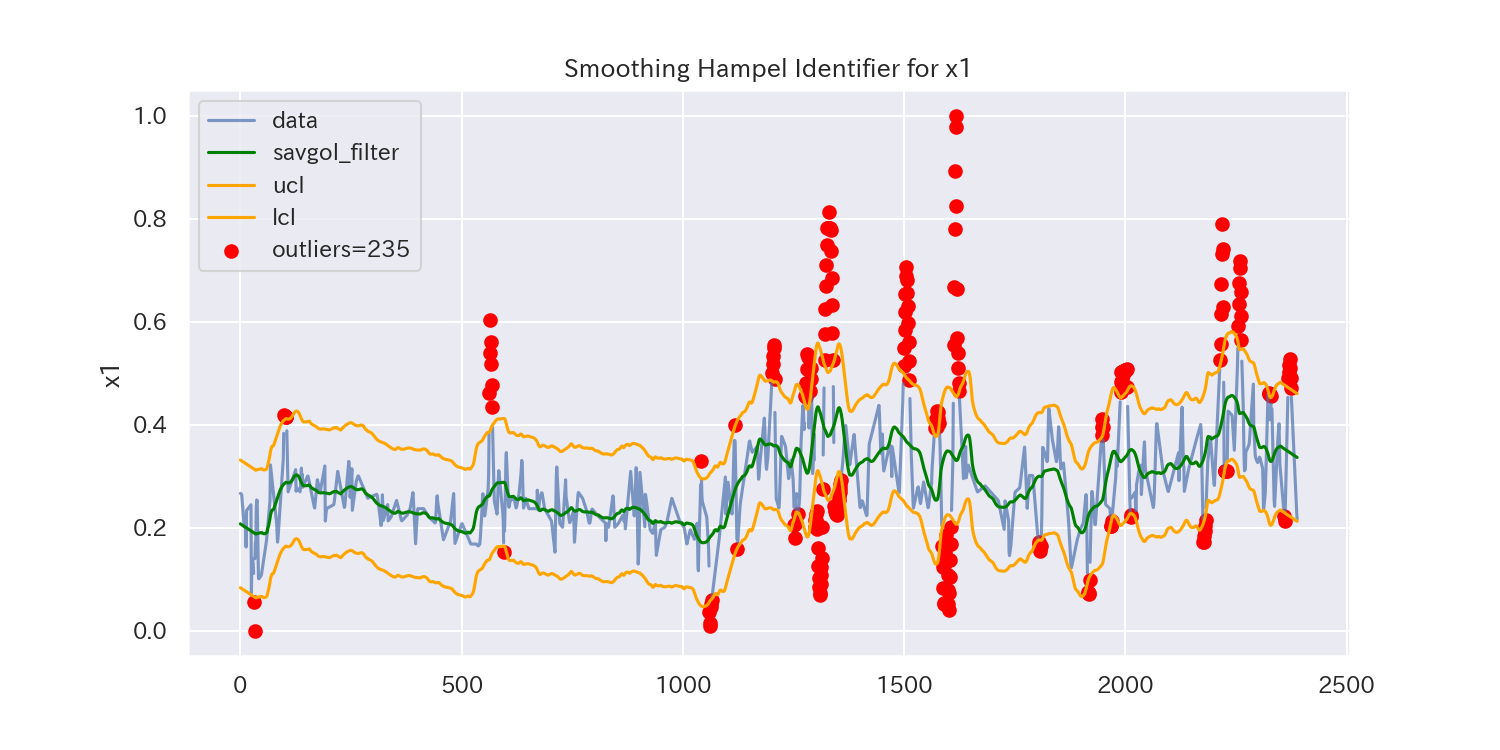
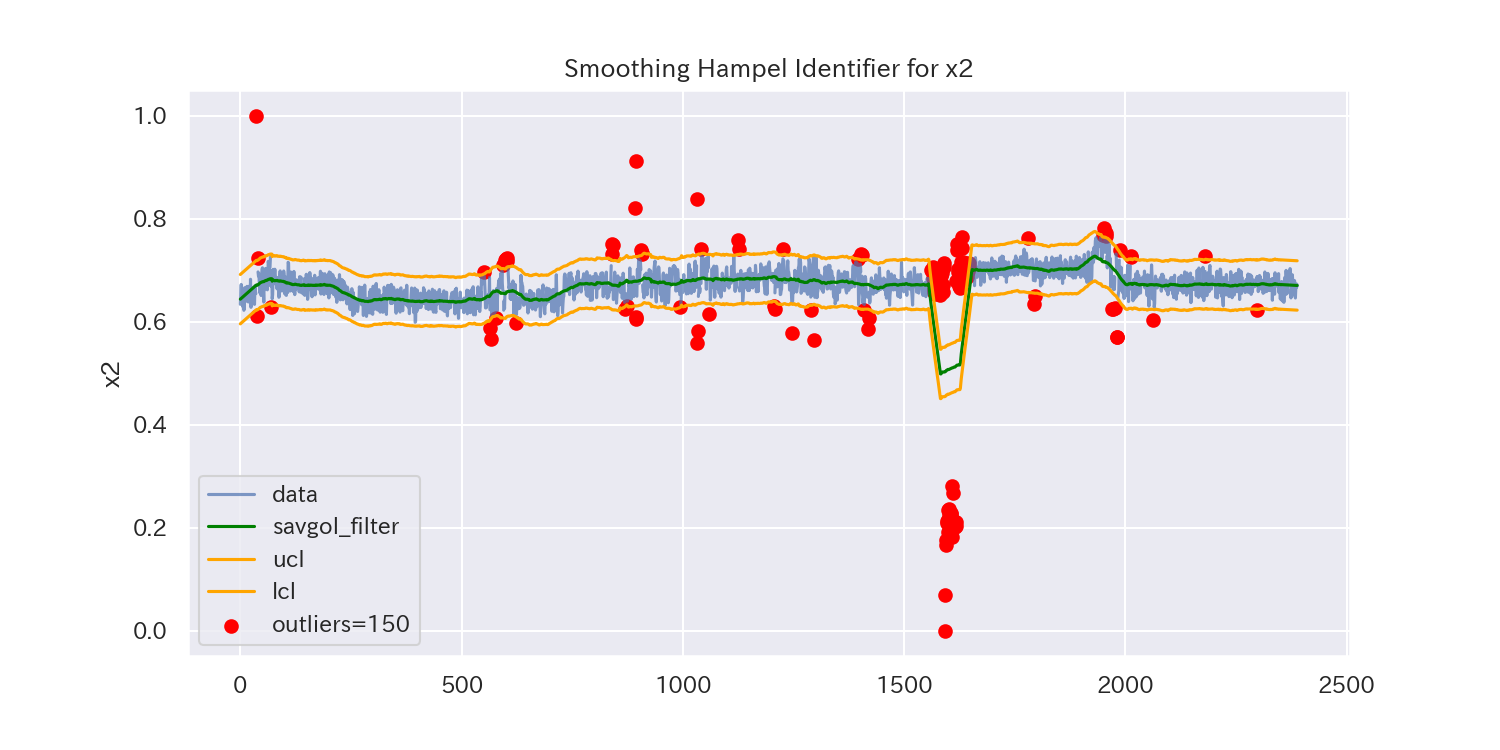
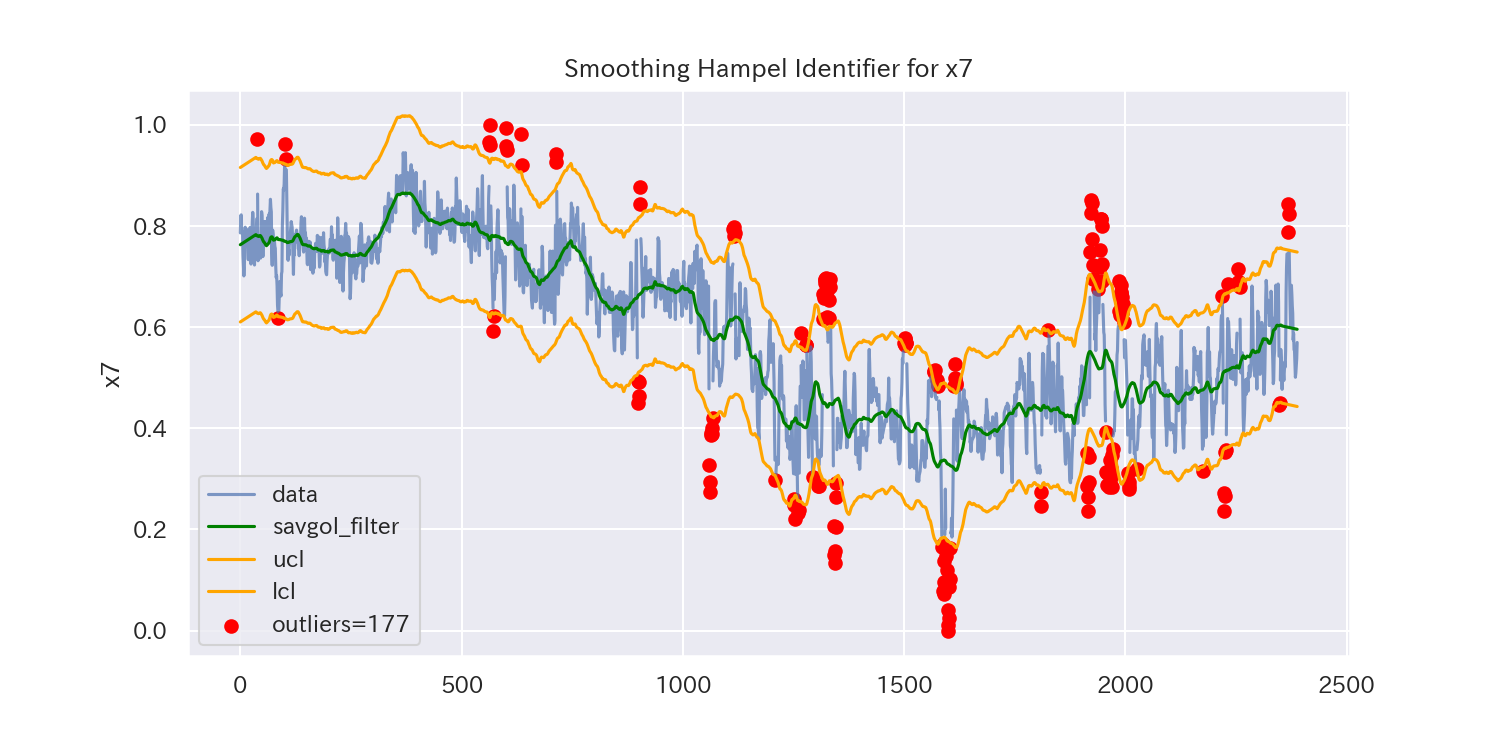
平滑化前後の差分に対してHampel Identifierを適用することで、'x7'のようなトレンドのあるデータでも外れ値を検出できるようになりました。
しかし、外れ値とは言えないデータも除去されている可能性があります。
平滑化パラメータによって検出される外れ値が変化しますので、外れ値を適切に除去できるように平滑化パラメータを微調整しましょう。
まとめ
まとめ
- 3シグマ法は、シンプルで理解しやすい反面、平均値と標準偏差が外れ値の影響を受けてしまい、閾値が大きくなり適切に外れ値を除去できない可能性がある。
- Hampel Identifierでは、中央値と中央絶対偏差(MAD)を用いるため、外れ値に対して頑健(ロバスト)な手法。
ただし、トレンドのあるデータに対しては、外れ値の検出精度は高くない。 - 平滑化前後の差分に対してHampel Identifierを適用する場合、トレンドのあるデータに対しても適切に外れ値を検出できようになるが、平滑化パラメータを試行錯誤する必要があり、難易度が上がる。
参考文献
Hampel Identifierはこちらの書籍で学びました。
化学・化学工学のための実践データサイエンス〜Pythonによるデータ解析・機械学習〜
平滑化手法やその他のpythonコードはこちらの書籍を参考にしています。
平滑化前後の差分に対してHampel Identifierを適用する手法は、こちらの記事を参考にしました。


