【python】ステップワイズ法による入力変数選択

どうも。こんにちは。
ケミカルエンジニアのこーしです。

本日は、ステップワイズ法による入力変数（特徴量）選択について解説します。

回帰分析の変数選択手法として有名なステップワイズ法をpythonで実装してみました。

pythonの有名なライブラリ(scikit-learnやstatsmodelsなど)には、ステップワイズ法が実装されてないため自作の関数を作成します。

初心者にも扱いやすい内容ですので、本記事を読みながらぜひ一度手を動かしてみてください。

※本記事では、ステップワイズ法のうち変数増加法についてのみ解説します。

この記事を書いた人

こーし(@mimikousi)

ステップワイズ法とは

まず、ステップワイズ法とは何か簡単に説明します。

ステップワイズとは、日本語にすると「段階的に」や「一歩ずつ」という意味になります。

よって、ステップワイズ法は下記のように表現できます。

入力変数を一つずつ取り込んだり取り除いたりしながら、回帰モデルを構築してモデルの適合度を評価し、最適な入力変数の組み合わせを探索する方法

　引用）スモールデータ解析と機械学習

モデルの適合度は、下記５つの評価関数から選ばれることが多いです。

また、ステップワイズ法には下記4種類の方法があります。

ステップワイズ法といえば、3.変数増減法を指すことが多いですが、本記事ではより簡単な「変数増加法」について解説します。

変数増加法のアルゴリズムは下記の通りです。

ステップワイズ法のアルゴリズムを簡単に書いてみましたが、もしイメージがつかみにくかったら、下記の記事がわかりやすいので参考にしてみてください。

【参考記事】

ステップワイズ法とは

評価関数（AIC、 BIC）

本記事で扱う評価関数は、下記の２種類です。

赤池情報量規準（AIC）

AICでは、下記２つのバランスを評価します。

• データへの統計モデルのあてはまりのよさ
• 統計モデルの簡潔さ（説明変数の少なさ）

そのモデルにおける当てはまりのよさを表す最大尤度を\(L\)、説明変数の数を\(k\)とおくと、AICは下式となります。

$$\textrm {AIC} = -2\log L + 2k\tag{1}$$

そして、AICが最小となるモデルを選択します。

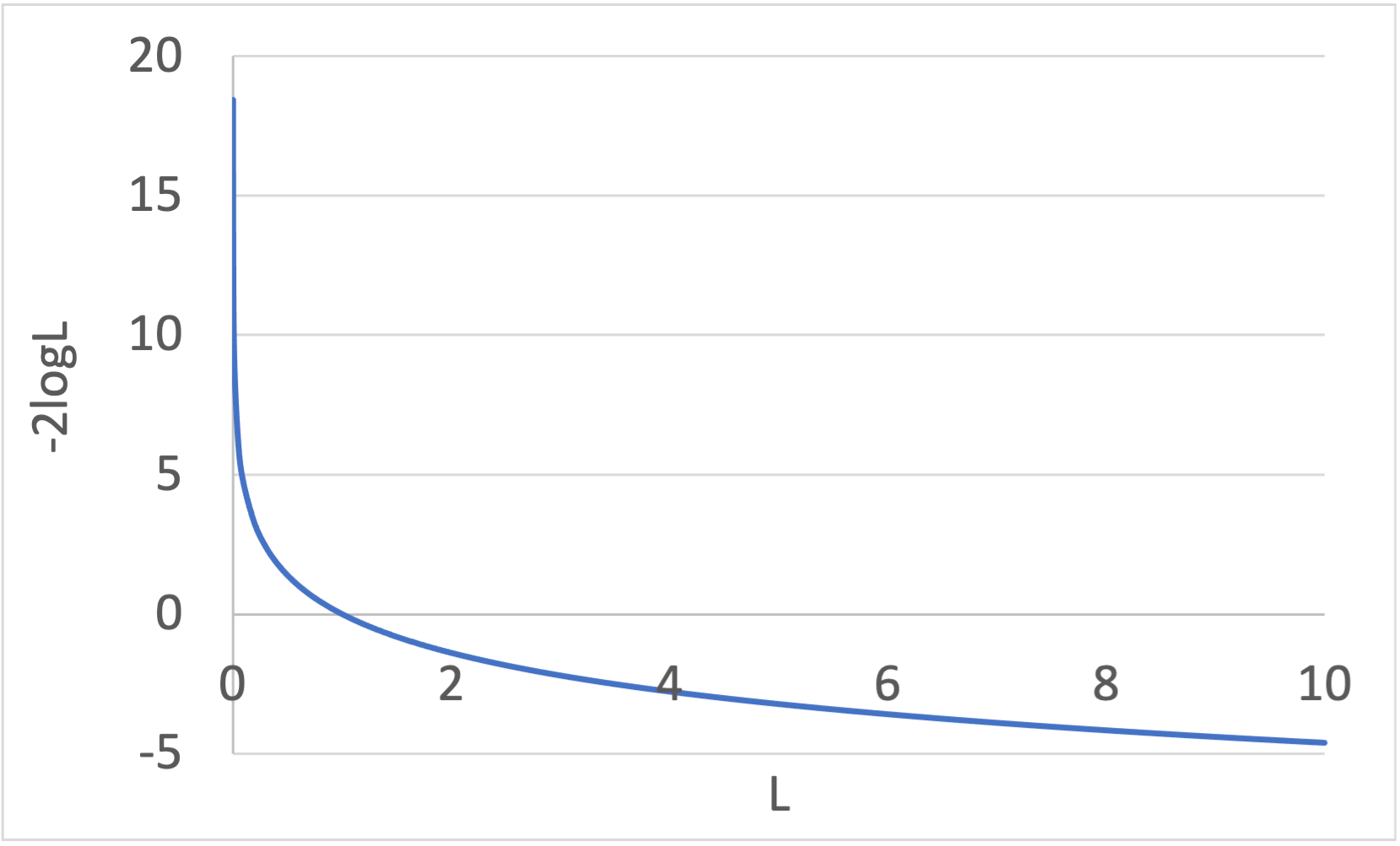
（１）式の第１項\(-2\log L\)は、最大尤度\(L\)の増加に従って単調に減少しますが、その減少幅はしだいに小さくなっていきます（下図参照）。

一方、第２項の\(+2k\)は説明変数の数\(k\)に比例して増加しますので、どこかで説明変数増加の影響の方が大きくなります。

よって、最大尤度\(L\)と説明変数の数\(k\)がバランスした点がAIC最小となり、説明変数を増やし過ぎない程よいモデルと言えます。

また、線形回帰モデルにおける\(i\)番目のサンプル\(x_i\)の推定値についての誤差\(\epsilon_i\)が平均0、分散\(\sigma^2\)の正規分布\(\mathcal{N}(0,\sigma^2)\)に従うと仮定すると、対数尤度関数は下式のように書けます。

簡単のために、残差平方和\(\textrm {RSS} \)を導入しましょう。

$$\textrm {RSS} = \sum_{i  = 1}^N\Big((y_i - \beta^\top x_i)^2\Big)\tag{3}$$

(2)式を残差平方和\(\textrm {RSS} \)を使って表すと、対数尤度関数は下式のように書き直せます。

$$\log L(\beta) = - \frac{\textrm {RSS}}{2\sigma^2} - \frac{N}{2}\log(2\pi\sigma^2)\tag{4}$$

ここで、(4)式を\(\sigma^2\)で微分して0とおき整理すると、\(\sigma^2\)の最尤推定量\(\tilde{\sigma^2} \)が導けます。

$$\frac{\textrm {RSS}}{2(\sigma^2)^2} - \frac{N}{2\sigma^2} = 0$$

$$\tilde{\sigma^2} = \frac{\textrm{RSS}}{N}$$

これを(4)式に代入すると最大対数尤度は下式となります。

よって、最大対数尤度を(1)式のAICに代入します。

ここで、定数項である\(N\)や\(\log2\pi\)は、比較する際に不要であるため除きます。

$$\textrm{AIC} = N\log \frac{\textrm{RSS}}{N} + 2k\tag{7}$$

よって、評価すべきAICは(7)式となります。

ベイズ情報量規準（BIC）

AIC以外に有名な評価関数として、BICが提案されています。

BICは下式となります。

$$\textrm {BIC} = -2\log L + 2k\log N\tag{8}$$

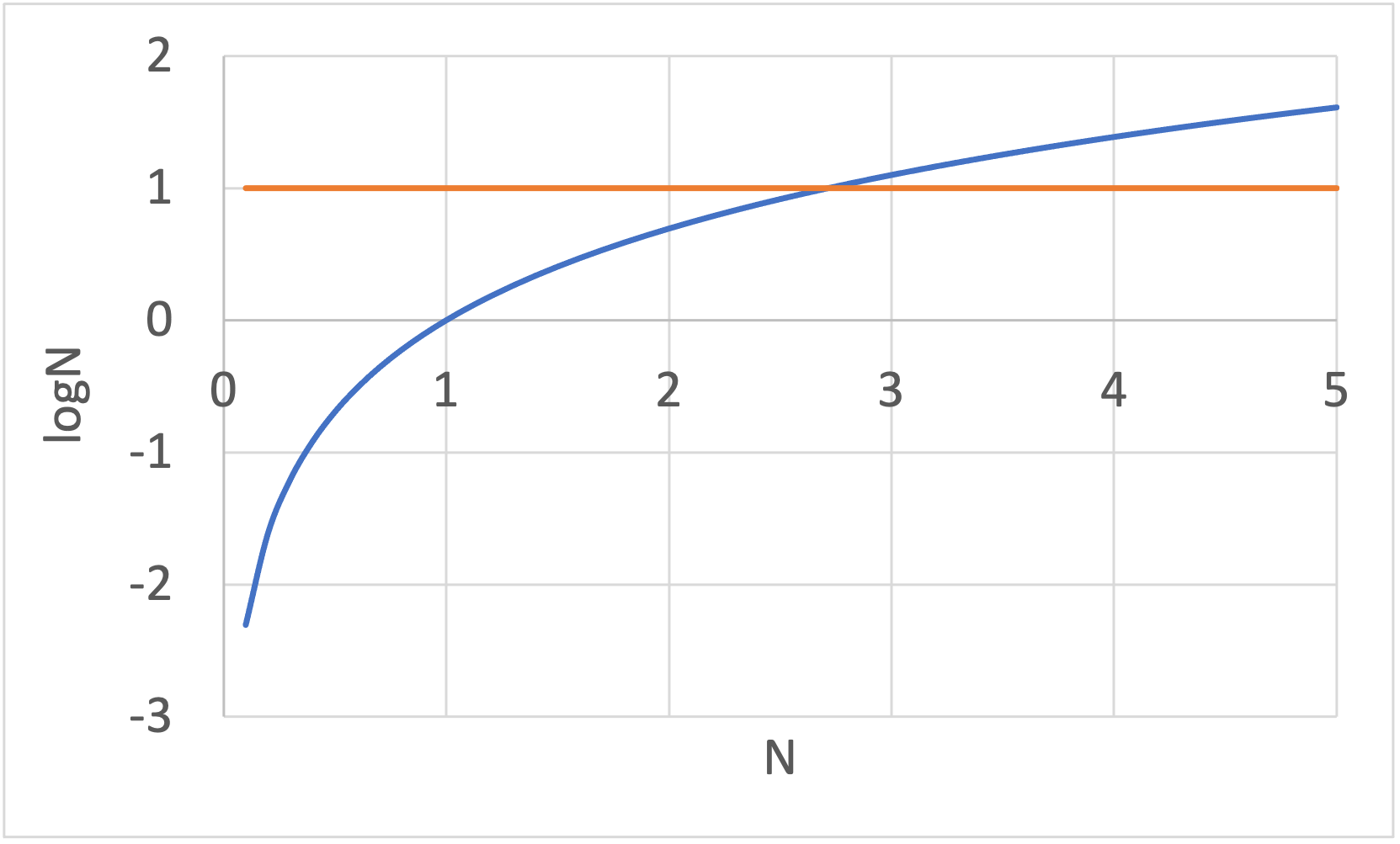
（１）式のAICと比較すると、第２項にサンプル数\(N\)が含まれています。

下図を見ればわかるように、\(N \geq 3\)のとき、\(\log N > 1\)となるため、\(N \geq 3\)ではAICよりも説明変数の数\(k\)のペナルティが厳しく、AICよりもBICの方がシンプルな（説明変数の少ない）モデルが選択される傾向があります。

AICと同様に、線形回帰モデルにおける\(i\)番目のサンプル\(x_i\)の推定値についての誤差\(\epsilon_i\)が平均0、分散\(\sigma^2\)の正規分布\(\mathcal{N}(0,\sigma^2)\)に従うと仮定すると、BICは下式のように変形できます。

$$\textrm{BIC} = N\log \frac{\textrm{RSS}}{N} + 2k\log N\tag{9}$$

変数増加法（forward-stepwise selection）

それではpythonで変数増加法を実装していきましょう。

データ準備

まず、データを準備します。

今回は、Harvard Dataverse で公開されているTennessee Eastman Process（TEP）のデータを使用します。

コチラのGitHubページに「normal_data.csv」がありますので、保存しましょう。

ちなみに、データを準備する方法は、下記の記事で解説しています。

データの内容

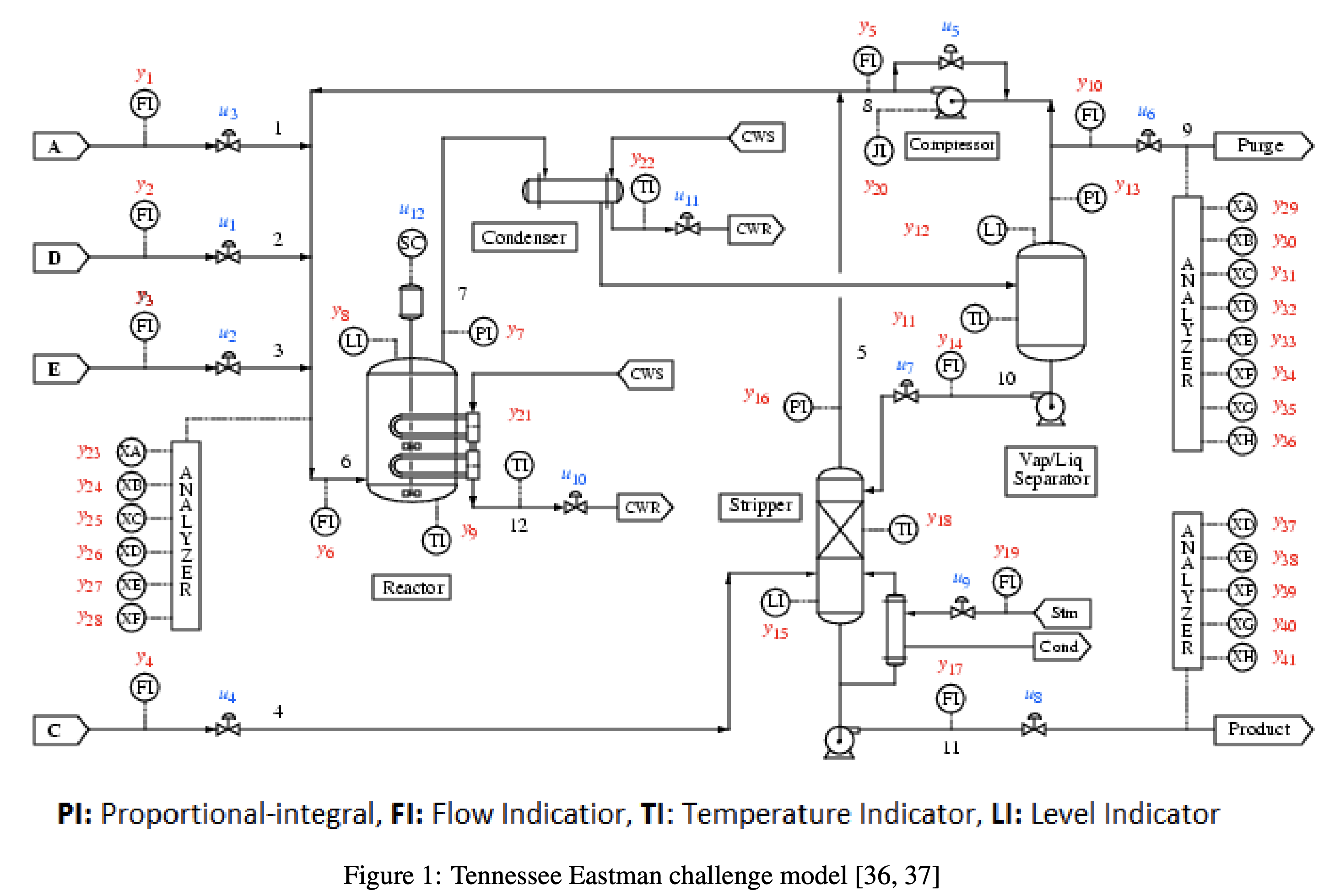
上図は、Tennessee Eastman Process（TEP）のプロセスフローダイアグラム（PFD）です。

TEPは下記5つの主要機器からなるプロセスで、A,C,D,Eの4つの原料から化学反応によってG,Hの2つの製品を製造します。

• 反応器（Reactor）
• 凝縮器（Condenser）
• 精留塔（Stripper）
• 気液分離機（Vap/Liq Separator）
• コンプレッサ（Compressor）

AIC、BIC、回帰係数βを求める関数

AIC、BIC、回帰係数βを求める関数を作成します。

「forward_stepwise_selection.py」というファイルを作成し、以下のコードを入力してください。

import numpy as np

# 赤池情報量基準
def AIC(x, y):
    beta = np.linalg.solve(x.T @ x, x.T @ y)　# 回帰係数を求めます。
    y_pred = x @ beta　# 予測値を求めます。
    resid = y - y_pred　# 残渣（実データ－予測値）を求めます。
    rss = resid.T @ resid # 残渣の二乗和を求めます。
    AIC = len(y) *np.log(rss/len(y)) + (x.shape[1])*2 # AICを求めます。
    return AIC

# ベイズ情報量基準
def BIC(x, y):
    beta = np.linalg.solve(x.T @ x, x.T @ y)　# 回帰係数を求めます。
    y_pred = x @ beta # 予測値を求めます。
    resid = y - y_pred # 残渣（実データ－予測値）を求めます。
    rss = resid.T @ resid # 残渣の二乗和を求めます。
    BIC = len(y) *np.log(rss/len(y)) + (x.shape[1])*np.log(len(y)) # BICを求めます。
    return BIC

# 変数選択後のサンプルデータから回帰係数を求めます。
def forward_stepwise_result(x, y):
    beta = np.linalg.solve(x.T @ x, x.T @ y)
    return beta

ちなみに、多用している@演算子はpython3.5以降で使えるようになった演算子で、numpyのmatmulやdotに相当します。

変数増加法（forward-stepwise selection）

続いて、変数増加法を行う関数を作成します。

先ほど作成した「forward_stepwise_selection.py」というファイルに以下のコードを追記しましょう。

# forward_stepwise selection
def forward_stepwise(x, y, method='BIC'):
    """
    forward stepwise（変数増加法）で変数選択を行います。
        
    パラメータ
    ----------
        x :説明変数のデータセット 
        y :目的変数のデータセット
        method: 'AIC' or 'BIC'. Defaults to 'BIC'.

    戻り値
    ----------
        beta:回帰係数（最小二乗法）
        included_column:選択されたカラム名
        result_min: AICかBICの最終結果（最小値）
    """
    # xに要素１のintercept列を追加（0列目）
    x_tmp = np.concatenate(
        [np.reshape(np.ones(x.shape[0]), (x.shape[0],1)), x], axis=1
    ) # 要素１のarrayをn行１列にreshapeし、xと結合
    included = list([0]) #intercept列のみ（初期値）
    while True:
        changed = False
        excluded = list(set(np.arange(x_tmp.shape[1]))-set(included) ) #　除外した（未採用）列の番号list
        result = np.zeros(len(excluded)) #AIC,BICの計算結果を格納する変数
        if method == 'AIC':
            base_result = AIC(x_tmp[:, included], y) # 採用列のデータのみでAICを計算
        else:
            base_result = BIC(x_tmp[:, included], y) # 採用列のデータのみでBICを計算
        print('Baseline model with {}:{:}'.format(method, base_result))
        j = 0
        for new_column in excluded:
            if method == 'AIC':
                result[j] = AIC(x_tmp[:, included + [new_column]], y) # 採用列以外の列を追加してAICを順番に計算する
            else:     
                result[j] = BIC(x_tmp[:, included + [new_column]], y) # 採用列以外の列を追加してBICを順番に計算する
            # print('Add:{:15} with {}: {:}'.format(excluded[j], method,result[j])) # コメントアウト
            j += 1
        if result.min() < base_result:
            best_feature = excluded[result.argmin()] # argmin():最小値を取るインデックスを返す
            included.append(best_feature) # 最小値を取る列数をincluded（採用列）に追加
            changed = True
            print('Finally Add {:15} with {} {:}'.format(best_feature, method, result.min()))
        if not changed: #changed=Falseのとき
            print('Any variables does not added, stop forward stepwise regression')
            break
            # end while
                
    # final resultの回帰係数を返す
    beta = np.reshape(np.zeros(x_tmp.shape[1]), (x_tmp.shape[1],1)) # 回帰係数を格納する変数
    beta = forward_stepwise_result(x_tmp[:, included], y) # 回帰係数を計算
    included.pop(0) # intercept列は除去
    included_r = [ i - 1 for i in included] # xのcolumn numberに変更（included - 1）
    included_column = x.columns[[included_r]] # 採用した列名を取得
    result_min = base_result # 最小値を取得
    
    return beta, included_column, result_min

これで、変数増加法（forward-stepwise selection）のモジュールが作成できました。

実行結果

それでは、TEPのデータを用いて実際に変数選択をやってみましょう。

ファイル名「TEP_forward_stepwise.ipynb」を作成し、下記コードを入力します。

import pandas as pd
import numpy as np
from forward_stepwise_selection import AIC, BIC, forward_stepwise 

# 学習データの読み込み
df = pd.read_csv('normal_data.csv')

# xとyに分けます。
x1 = df.iloc[:, :39] # 説明変数 x
x2 = df.iloc[:, 40:]
x = pd.concat([x1, x2], axis=1)
y = df.iloc[:, 39] # 目的変数 y 

# 全変数を用いた場合のAIC
print('全変数AIC = ', AIC(x, y))

# 全変数を用いた場合のBIC
print('全変数BIC = ', BIC(x, y))

# AICによる変数増加法
beta_AIC, included_column_AIC, result_min_AIC = forward_stepwise(x, y, method='AIC')
print(beta_AIC)
print(included_column_AIC)
print(result_min_AIC)

# BICによる変数増加法
beta_BIC, included_column_BIC, result_min_BIC = forward_stepwise(x, y, method='BIC')
print(beta_BIC)
print(included_column_BIC)
print(result_min_BIC)

実行結果は、下記の通りです。

全変数を使ったときよりも、変数増加法で変数を絞った方がAIC、BIC共に小さくなっていることがわかります。

また、BICの方が変数増加のペナルティが大きいため、選択される変数が少なくなることも確認できました。

非常にシンプルな変数選択手法ですので、ぜひ使いこなしてみてください。

参考文献

スモールデータ解析と機械学習

ステップワイズ法の概要と評価関数については、こちらの書籍を参考にしました。

その他、下記サイトも参考にしてます

①ステップワイズ法とは

　こちらの記事でさくっと概要をつかむと良いですね。

②pythonでstepwise regression用の関数を作っておく

　本記事では、こちらの記事を主に参考にさせてもらいました。

③pythonのstatsmodelsを使った重回帰分析で溶解度予測：AICによるモデル選択

　データを用意するところから、かなり詳しく書かれている記事です。