どうも。こんにちは。
ケミカルエンジニアのこーしです。
本日は、「正規性の検定(コルモゴロフ・スミルノフ検定)」についてわかりやすく解説します。
品質管理で用いられる「3σ管理」は、データが正規分布に従うことが前提です。
このように正規分布を前提とする統計的分析手法が数多くあるため、得られたデータが「正規分布に従うかどうか」を把握することは非常に重要です。
そこで、本記事ではpythonを駆使して正規性の検定を簡単に行う方法を解説します。
「正規性の検定」を適切に行い、データ分析の信頼性を高めましょう!
本記事の内容
・正規性の検定とは
・シャピロ・ウィルク検定
・コルモゴロフ・スミルノフ検定
・プロセスデータの正規性の検定
・参考文献
この記事を書いた人

こーし(@mimikousi)
目次
正規性の検定とは
正規性の検定とは、与えられたデータセットが正規分布(ガウス分布とも呼ばれる)に従っているかどうかを検定する手法のことです。
統計的手法やモデルの多くは、「データが正規分布に従う」という前提で構築されているため、正規性の検定は極めて重要となります。
正規分布を前提とする統計的手法の代表例を下記に示します。
正規分布を前提とする統計的手法
- 3σ管理
- t検定(平均値検定)
- 分散分析
- 線形回帰分析
など
正規性の検定方法
正規性の検定方法はいくつかありますが、本記事では有名な下記3つを紹介します。
正規性の検定方法
- 正規確率プロット(正規QQプロット)
- シャピロ・ウィルク検定
- コルモゴロフ・スミルノフ検定
正規確率プロット(正規QQプロット)
視覚的な方法にはなりますが、正規確率プロットはサンプルデータと正規分布に従う場合の理論値を比較して、グラフ上にプロットし直線上に乗るかどうかを確認します。
正規確率プロットについては、別記事で詳しく解説しています。
-

-
【python】正規確率プロット(正規QQプロット)の作成方法
続きを見る
シャピロ・ウィルク検定
シャピロ・ウィルク検定は、正規確率プロットにおける直線への当てはめの良さを表す指標を用いた検定方式です。
検定結果を確認するために、サンプルデータを準備します。
import numpy as np
import pandas as pd
from scipy.stats import shapiro, kstest, norm
import matplotlib.pyplot as plt
import japanize_matplotlib
import seaborn as sns
sns.set(font='IPAexGothic')
# 結果を再現可能にするためのシード値の設定
np.random.seed(42)
# サンプルサイズを設定
n = 50
# 正規分布データ
normal_data = np.random.randn(n)
# 二項分布データ(正規分布に従わない)
binomial_data = np.random.binomial(n=1, p=0.5, size=n)
# 対数正規分布データ(正規分布に従わない)
# mean (mu) と standard deviation (sigma) のパラメータを設定
mu, sigma = 0, 0.3
lognormal_data = np.random.lognormal(mean=mu, sigma=sigma, size=n)
# データをデータフレームに格納
df = pd.DataFrame({
'normal': normal_data,
'binomial': binomial_data,
'lognormal': lognormal_data
})
サンプルデータとして、正規分布に従うデータと正規分布に従わないデータ(二項分布と対数正規分布)を用意しました。
ヒストグラムを確認してみましょう。
# ヒストグラムと正規分布の曲線を描画
for col in df.columns:
fig, ax = plt.subplots(figsize=(8, 6))
df_col = df[col].dropna()
# ヒストグラムのbinの数を計算(スタージェスの公式)
num_bins = int(np.log2(len(df_col)) + 1)
# ヒストグラム
ax.hist(df_col, bins=num_bins, density=True, alpha=0.7, color='blue', label='Histogram')
# 正規分布曲線の描画
xmin, xmax = ax.set_xlim()
x = np.linspace(xmin, xmax, 100)
mu, std = norm.fit(df_col)
p = norm.pdf(x, mu, std)
ax.plot(x, p, 'k', linewidth=2, label='Normal distribution')
ax.set_xlabel('value')
ax.set_ylabel('Frequency')
title = f"Fit results: mu = {mu:.2f}, std = {std:.2f}"
ax.set_title(title)
plt.legend()
plt.show()
fig.savefig(f'{col}_histogram.png', dpi=100)
plt.close(fig)
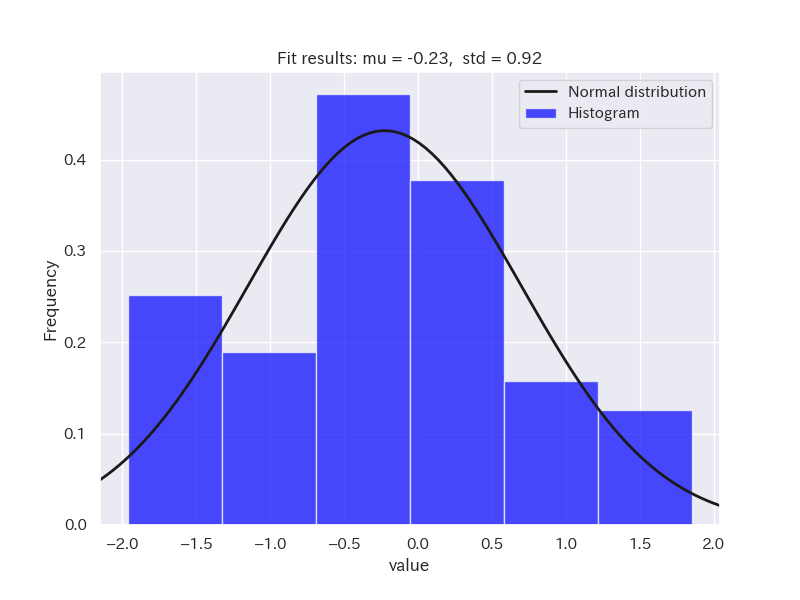
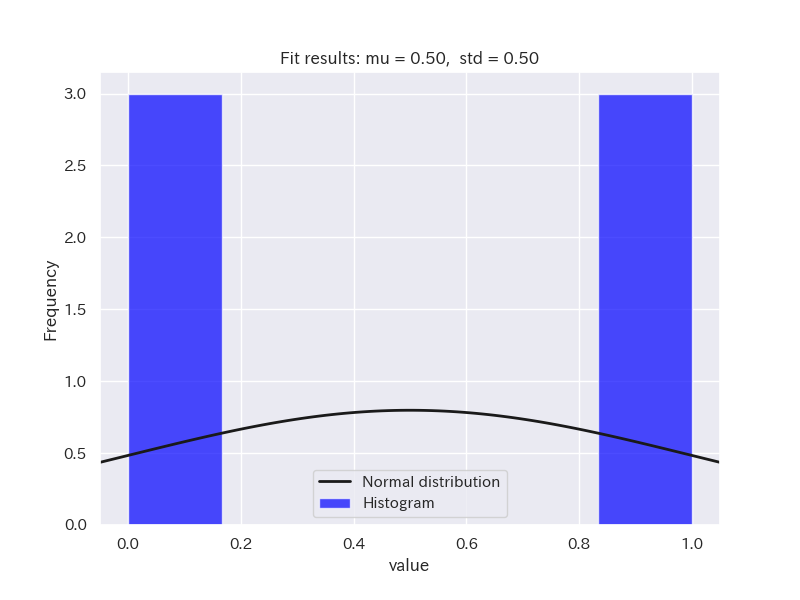
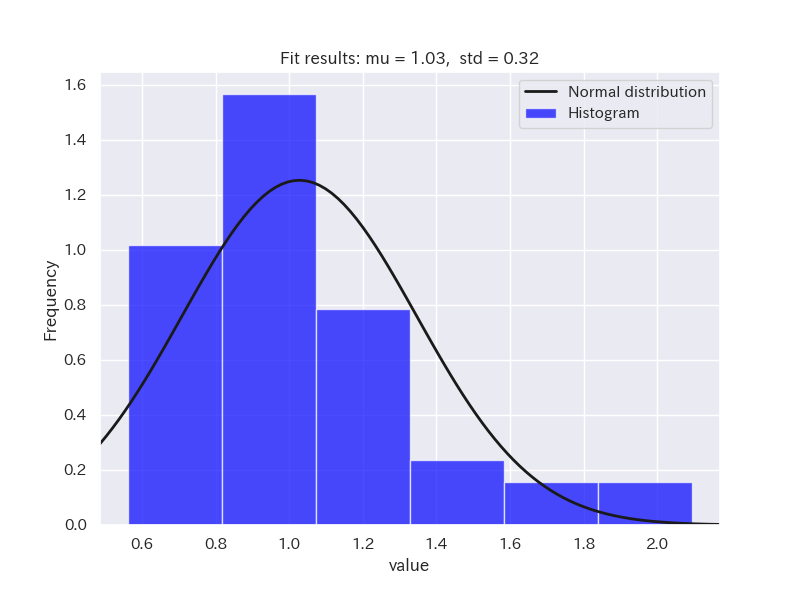
それでは、シャピロ・ウィルク検定を行ってみます。
# 結果を格納するデータフレームを作成
results = pd.DataFrame(columns=['column', 'pvalue', 'sample_size'])
# シャピロ・ウィルク検定
for col in df.columns:
df_col = df[col].dropna()
_, pvalue = shapiro(df_col)
sample_size = len(df_col)
# 結果をデータフレームに追加
results = results.append({'column': col, 'pvalue': pvalue, 'sample_size': sample_size}, ignore_index=True)
# データフレームをエクセルに保存
results.to_excel('shapiro_wilk_test_results.xlsx', index=False)
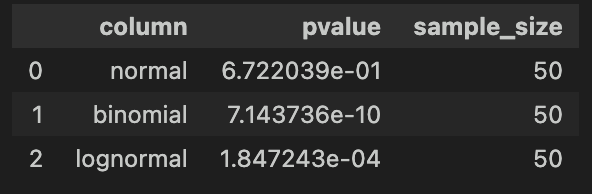
シャピロ・ウィルク検定とコルモゴロフ・スミルノフ検定の結果の解釈にはp値(p-value)を用います。
正規性の検定では、正規分布に従うことを帰無仮説と設定しますので、p値が特定の有意水準(よく使用されるのは0.05)より小さい場合、データは正規分布に従っていないと解釈されます。
よって、今回サンプルデータでは二項分布、対数正規分布ともに\(p < 0.05\)であるため、正規分布に従っていないと言えます。
シャピロ・ウィルク検定で正しく正規性を検定できました。
コルモゴロフ・スミルノフ検定(KS検定)
コルモゴロフ・スミルノフ検定(KS検定)は、該当データの経験分布関数と理論分布(正規分布)の累積分布関数の差の最大値を検定統計量に用います。
正規分布以外の分布(主に一様分布)にも使えますし、2つの分布(経験分布関数)を比較することもできます。
pythonコードは下記の通りです。
# 結果を格納するデータフレームを作成
results = pd.DataFrame(columns=['column', 'pvalue', 'sample_size'])
# コルモゴロフ・スミルノフ検定
for col in df.columns:
df_col = df[col].dropna()
# データの平均と標準偏差を計算
mean = df_col.mean()
std = df_col.std(ddof=1)
# 標準正規分布の平均と標準偏差を調整して検定
result = kstest(df_col, 'norm', args=(mean, std))
pvalue = result[1]
sample_size = len(df_col)
# 結果をデータフレームに追加
results = results.append({'column': col, 'pvalue': pvalue, 'sample_size': sample_size}, ignore_index=True)
# データフレームをエクセルに保存
results.to_excel('kolmogorov_smirnov_test_results.xlsx', index=False)
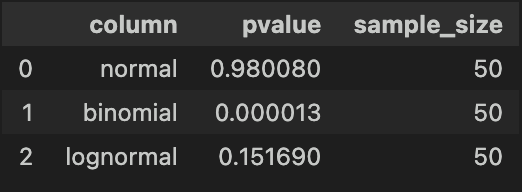
コルモゴロフ・スミルノフ検定では、二項分布は正しく検定できたものの、対数正規分布ではp値が大きくなり、帰無仮説を棄却できませんでした。
サンプルサイズが小さいとき(例えば50以下)は、シャピロ・ウィルク検定の方が好ましいようです。
サンプルサイズが大きいとき
サンプルサイズを50から500に変更してみます。
検定結果は下記の通りです。
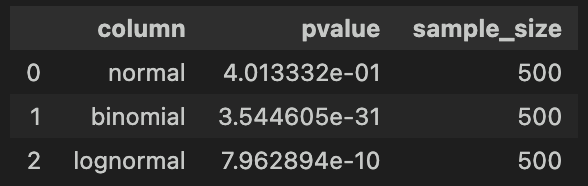
〇シャピロ・ウィルク検定
〇コルモゴロフ・スミルノフ検定
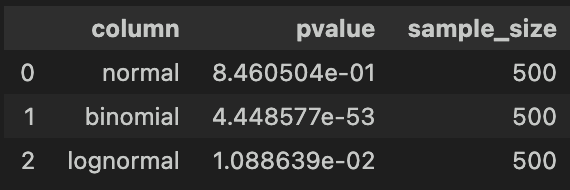
サンプルサイズが大きくなった場合は、コルモゴロフ・スミルノフ検定でも対数正規分布を「正規分布に従わない」と正しく検定できました。
一方、シャピロ・ウィルク検定はサンプルサイズが大きくなると、p値が非常に小さくなります。
よって、微小な偏差でも「正規分布に従わない」という結果が出やすくなる傾向があります。
正規性の検定の注意点
以上のことから下記ポイントに注意しましょう。
注意ポイント
- シャピロ・ウィルク検定は、サンプルサイズが小さい場合(例えば50以下)に有効。
ただし、サンプルサイズが大きくなると、微小な偏差でも統計的に有意になりやすい。 - コルモゴロフ・スミルノフ検定は、サンプルサイズが小さい場合、他の検定に比べて検出力が低い。
また、連続分布のデータにのみ適用でき、離散的なデータに対してはそのままの形式では使用できない。
プロセスデータにおける正規性の検定
プロセスデータの入手
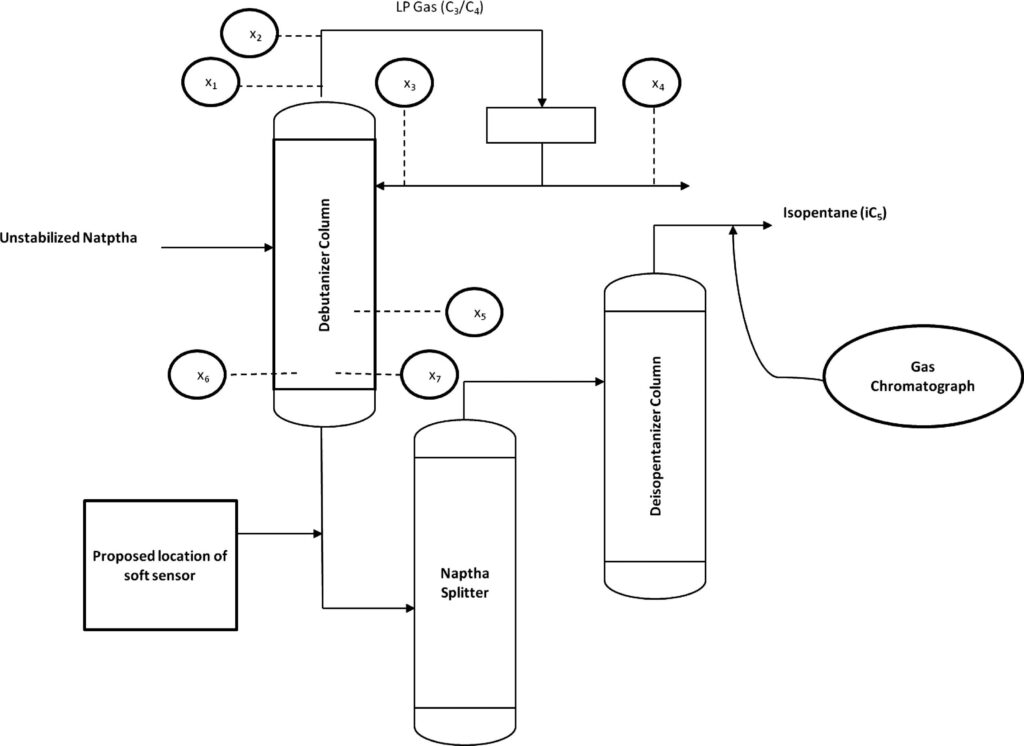
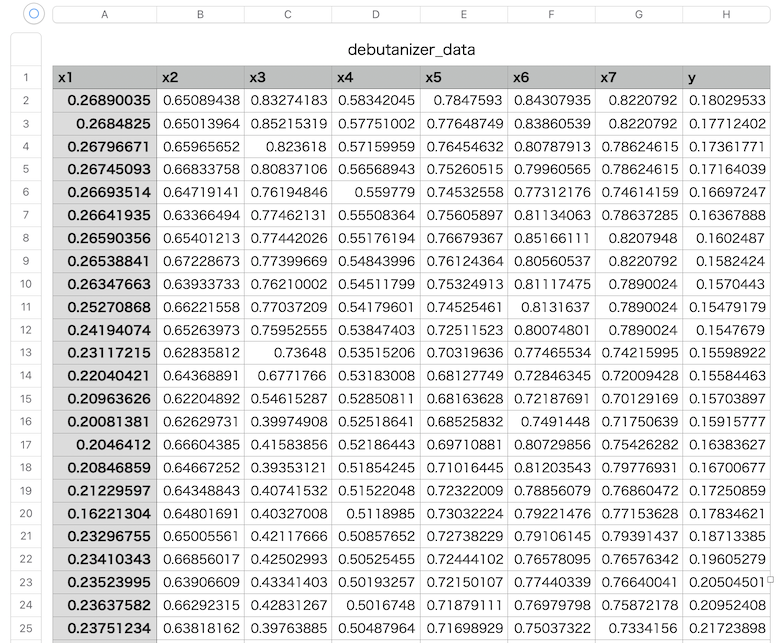
コチラのGitHubページで入手できる「debutanizer_data.csv」を利用します。
脱ブタン塔のプロセスデータであり、プロセスフローは上図の通りです。
説明変数がx1〜x7の7個で、目的変数がyの1個、サンプル数は2394個です。
| 変数名 | 詳細 | 日本語訳 |
|---|---|---|
| x1 | Top Temperature | 塔頂温度 |
| x2 | Top pressure | 塔頂圧力 |
| x3 | Reflux flow | 還流流量 |
| x4 | Flow to next process | 次プロセスへの流量 |
| x5 | 6th tray Temperature | 6段目温度 |
| x6 | Bottom Temperature1 | 塔底温度1 |
| x7 | Bottom Temperature2 | 塔底温度2 |
| y | Butane(C4) content in the debutanizer column bottom | 塔底におけるブタン含有量 |
データの読み込み
「debutanizer_data.csv」と同じフォルダに、「normality_test.ipynb」というファイルを作成しましょう。
下記のコードでライブラリのインポートと、データの読み込みを行います。
import pandas as pd
from scipy.stats import shapiro,kstest
#脱ブタン塔のプロセスデータを読み込む
df = pd.read_csv('debutanizer_data.csv')
データの可視化(ヒストグラム)
ヒストグラムを作成し、データの分布を確認しましょう。
さらに、ヒストグラムと正規分布(確率密度関数)を比較します。
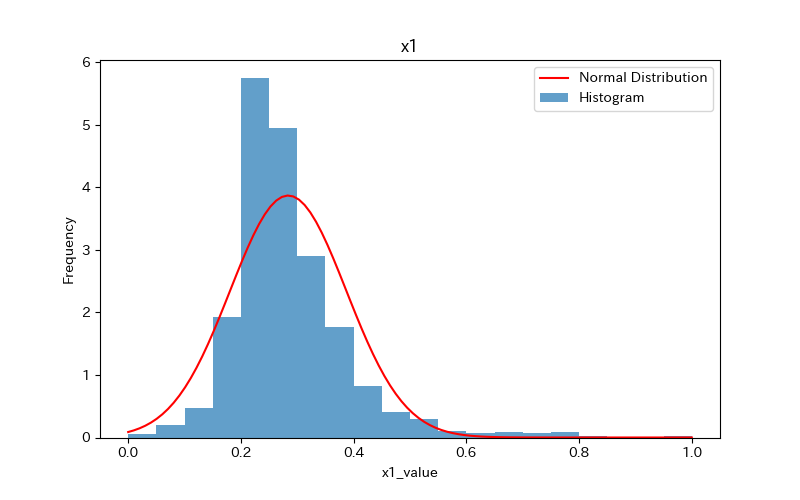
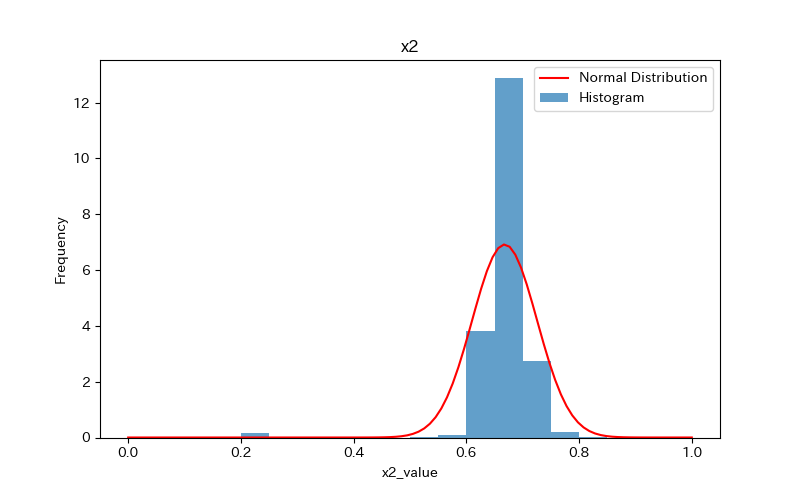
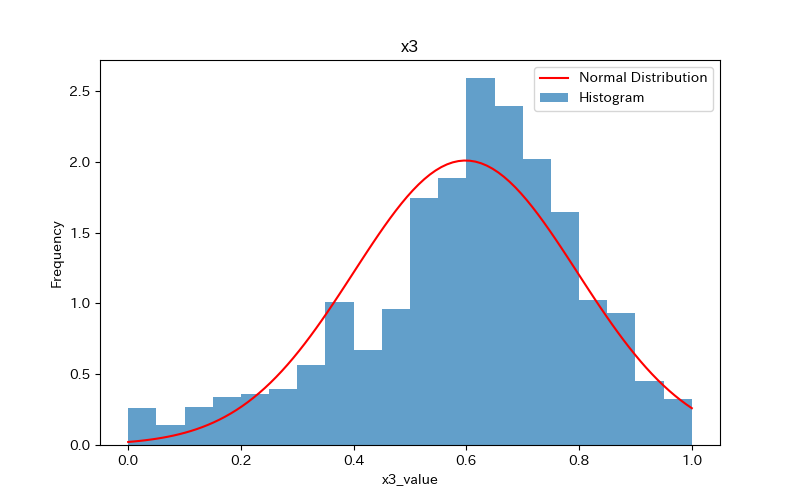
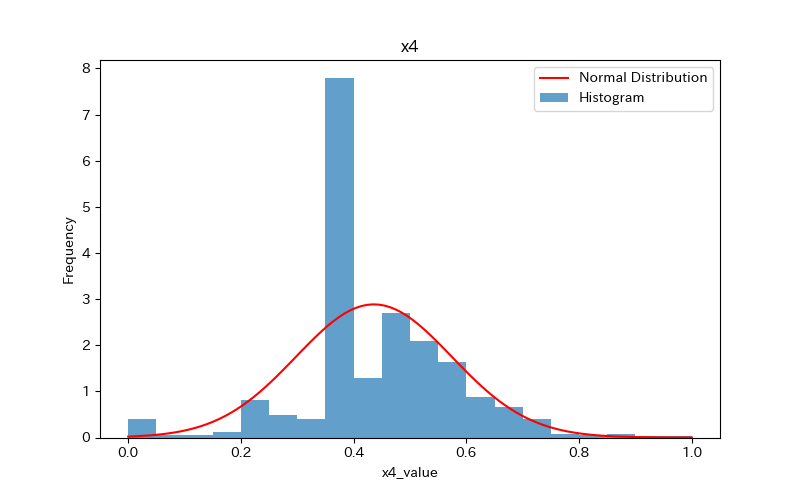
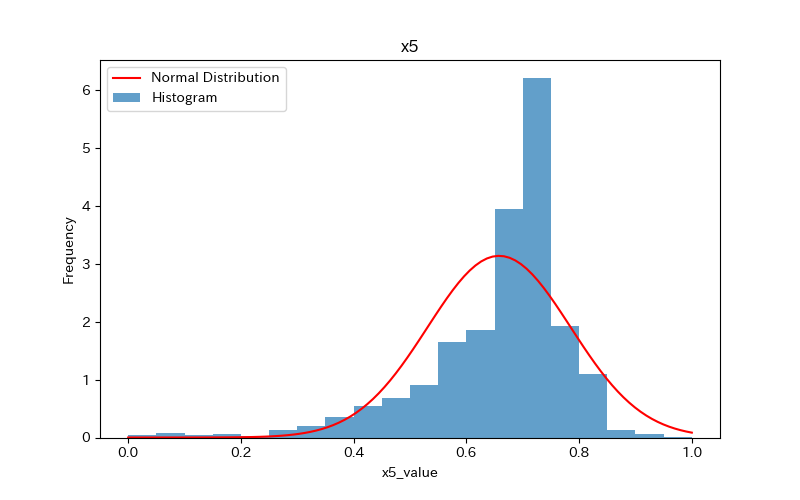
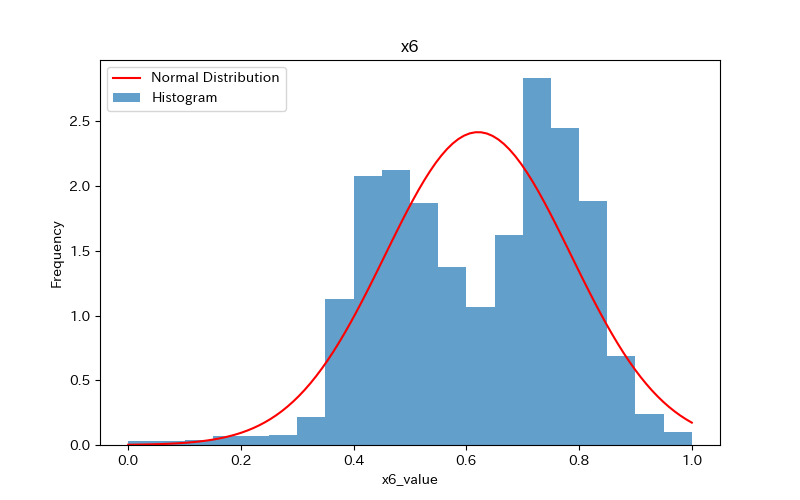
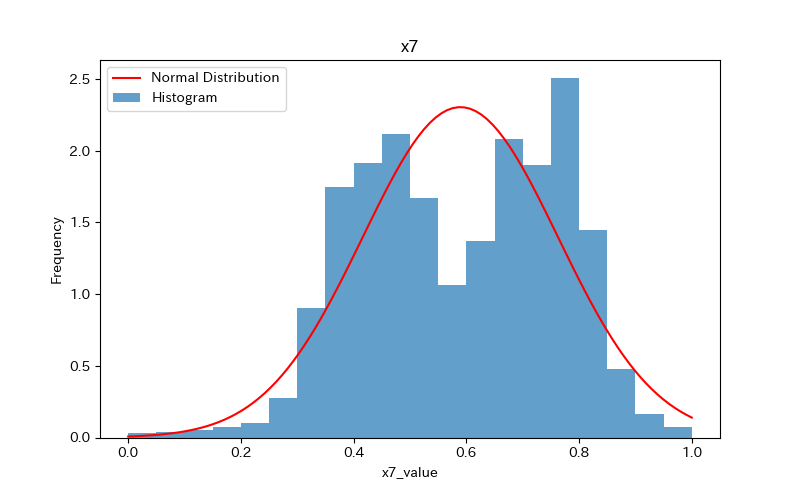
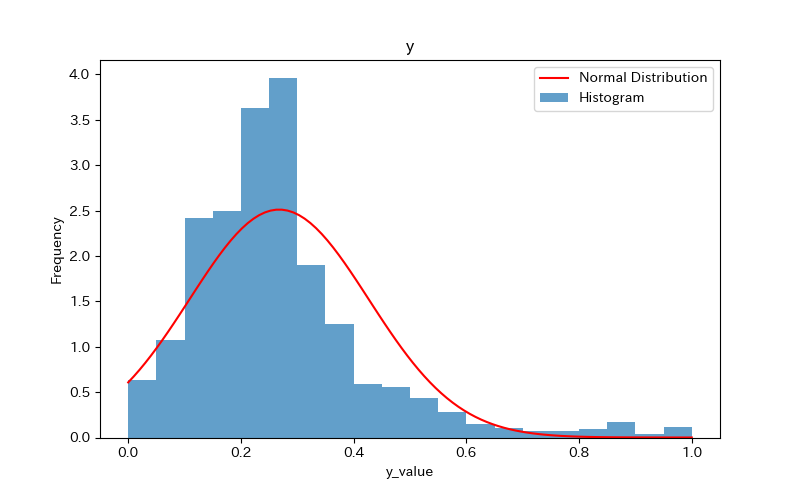
ヒストグラムの作成方法(pythonコード)については、下記で詳しく解説しています。
-

-
【python】ヒストグラムの作成方法(スタージェスの公式)
続きを見る
シャピロ・ウィルク検定
プロセスデータの各列データに対して、シャピロ・ウィルク検定を行いましょう。
# 結果を格納するデータフレームを作成
results = pd.DataFrame(columns=['column', 'pvalue', 'sample_size'])
# シャピロ・ウィルク検定
for col in df.columns:
df_col = df[col].dropna()
result = shapiro(df_col)
pvalue = result[1]
sample_size = len(df_col)
# 結果をデータフレームに追加
results = results.append({'column': col, 'pvalue': pvalue, 'sample_size': sample_size}, ignore_index=True)
# データフレームをエクセルに保存
results.to_excel('shapiro_wilk_test_results_debutanizer.xlsx', index=False)
検定結果は下図の通りです。
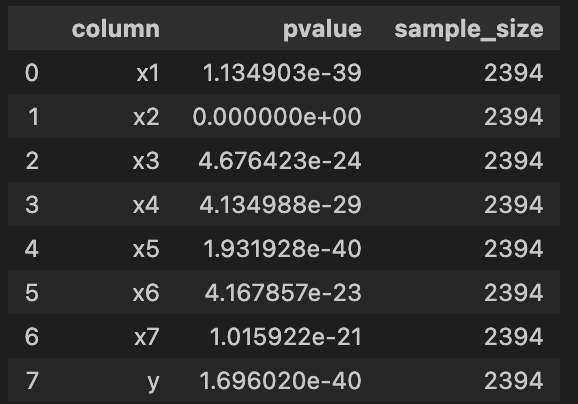
前述のヒストグラムを見て分かるように、どれもpvalueが0.05より小さく「正規分布に従わない」ことがわかります。
'x2'に至っては、分布が尖っているためかpvalueが計算できていません。
コルモゴロフ・スミルノフ検定(KS検定)
続いて、コルモゴロフ・スミルノフ検定も行いましょう。
pythonコードは下記の通りです。
# 結果を格納するデータフレームを作成
results = pd.DataFrame(columns=['column', 'pvalue', 'sample_size'])
# コルモゴロフ・スミルノフ検定
for col in df.columns:
df_col = df[col].dropna()
# データの平均と標準偏差を計算
mean = df_col.mean()
std = df_col.std(ddof=1)
# 標準正規分布の平均と標準偏差を調整して検定
result = kstest(df_col, 'norm', args=(mean, std))
pvalue = result[1]
sample_size = len(df_col)
# 結果をデータフレームに追加
results = results.append({'column': col, 'pvalue': pvalue, 'sample_size': sample_size}, ignore_index=True)
# データフレームをエクセルに保存
results.to_excel('kolmogorov_smirnov_test_results_debutanizer.xlsx', index=False)
検定結果は下図の通りです。
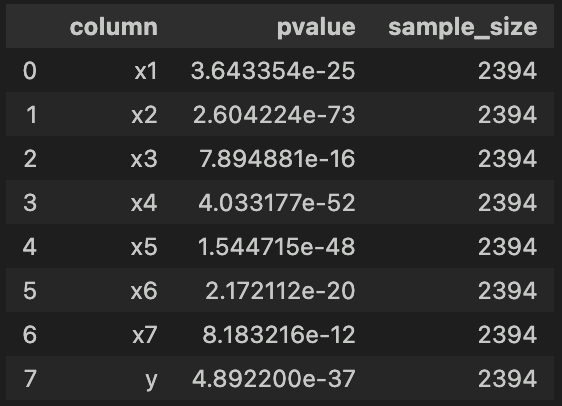
シャピロ・ウィルク検定と同様、どれもpvalueが0.05より小さく「正規分布に従わない」ことがわかります。
ただし、コルモゴロフ・スミルノフ検定では'x2'のpvalueが計算できるようになっています。
今回のデータのようにサンプルサイズが大きい場合は、コルモゴロフ・スミルノフ検定を使う方が良さそうです。
まとめ
正規性の検定は、統計的分析を行う上でとても重要です。
データが正規分布に従うかどうかを確認することで、その後の分析や検定の信頼性を確保することができます。
検定方法の選択は、データの特性やサンプルサイズに応じて慎重に行いましょう。
まとめ
- 検定結果(p値)が、有意水準(0.05)よりも小さい場合、「データは正規分布に従わない」
- データ数(サンプルサイズ)が50以下と小さい場合、シャピロ・ウィルク検定を使う
- データ数(サンプルサイズ)が大きい場合は、コルモゴロフ・スミルノフ検定(KS検定)を使う
参考文献
本記事では、こちらの書籍を参考にしました。
正規性の検定の理論部分が詳しく解説されています。
Rコードが少し記載されているのみで、pythonやexcelで実行する方法については触れていないので注意が必要です。


