どうも。こんにちは。
ケミカルエンジニアのこーしです。
本日は、「プロセスデータにおける機械学習の解釈(SHAP)」について書いていきます。
機械学習を用いると、データから高精度の予測モデルを構築できます。
しかし、予測結果がどのように導かれたのかを理解するのは、しばしば困難です。
つまり、「予測精度」と「解釈性」のトレードオフが存在します。
そこで本記事では、「機械学習を解釈する技術」という本で紹介されているPFI、PD、ICE、SHAPといった機械学習の解釈手法を、化学プラントのプロセスデータを題材に解説します。
本記事の内容
・機械学習の解釈手法
・データの可視化
・回帰モデルの作成
・PFI,PD,ICE,SHAPの可視化
この記事を書いた人

こーし(@mimikousi)
機械学習の解釈手法
本記事では、下記4つの解釈手法についてプロセスデータに適用してみます。
4つの解釈手法
- Permutation Feature Importance(PFI)
→特徴量の重要度 - Partial Dependence(PD)
→特徴量と予測値の平均的な関係性 - Individual Conditional Expectation(ICE)
→インスタンス毎の特徴量と予測値の関係性 - SHapley Additive exPlanations(SHAP)
→特徴量ごとの貢献度(予測の理由)
以下、それぞれの解釈手法について簡単に説明します。
Permutation Feature Importance(PFI)
PFIでは、特徴量の値をシャッフルしたときの「予測誤差の増加分」を特徴量の重要度と見なします。
例えば、シャッフルすると予測誤差がとても大きくなってしまう場合、その特徴量はモデルの予測に大きく寄与していると考えることができます。
注意ポイント
- 強く相関する特徴量が存在するとき、重要度の食い合いが発生してしまう。
- モデルの予測値にどのように影響を与えているのかがわからない。
Partial Dependence(PD)
PDは、他の特徴量を固定し、興味のある特徴量だけを動かし、各インスタンス(サンプルや行データのこと)の予測値を平均して可視化することで、特徴量と予測値の関係性を知ることができる解釈手法です。
つまり、ある特徴量が大きくなった場合に、予測値が大きくなるのか、あるいは小さくなるのかを把握することができます。
PFIで重要な特徴量を把握し、そのあとPDで重要な特徴量と予測値の関係を見るといった使い方になります。
注意ポイント
PDは平均的な関係に注目しているため、ひとつひとつのインスタンスにおいて特徴量と予測値の関係が異なる場合は、その影響を考慮できないので注意が必要です。
Individual Conditional Expectation(ICE)
PDでは、平均的な関係に注目していましたが、ICEでは平均をとらず、ひとつひとつのインスタンスに対して特徴量と予測値の関係を確認する手法です。
平均的な傾向と異なる動きを見せるインスタンスが存在する場合、このようなインスタンスについて他の特徴量を確認することで分析を深めていくことができます。
注意ポイント
特徴量と予測値の関係を知ることはできますが、「モデルがなぜこのような予測値を出したのか」という予測の理由までは知ることができません。
SHapley Additive exPlanations(SHAP)
SHAPは、協力ゲーム理論における Shapley値のコンセプトを機械学習に応用したものです。
「あるインスタンスに対する予測値」を「平均的な予測値」と「特徴量ごとの貢献度」に分解することで、なぜモデルがそのような予測値を出したのかを知ることができます。
特徴量の貢献度として、ある特徴量の値が「わかっている」ときと、「わかっていない」ときの予測値の差分を用います。
注意ポイント
- 特徴量が変化した際に予測値がどう反応するかはわからない(ICEを併用する)
- 計算コストが高い
全体に共通する注意点
上記4つの解釈手法を、「因果関係」として解釈することは非常に危険です。
もし、因果関係をはっきりさせたいという目的であれば、「因果推論」という手法を使いましょう。
下記のような使い方なら問題ないと言えます。
ポイント
- モデルのデバック
ドメイン知識と整合性があるか - モデルの振る舞いの解釈
例)モデルは特徴量Aを重視している
例)特徴量Aが大きくなると予測値も大きくなる
※間違った解釈をしている可能性もあるため注意。
より詳しい解説は、下記書籍を参照してください。
とてもわかりやすいので初心者でも読みこなせると思います。
サンプルデータの入手
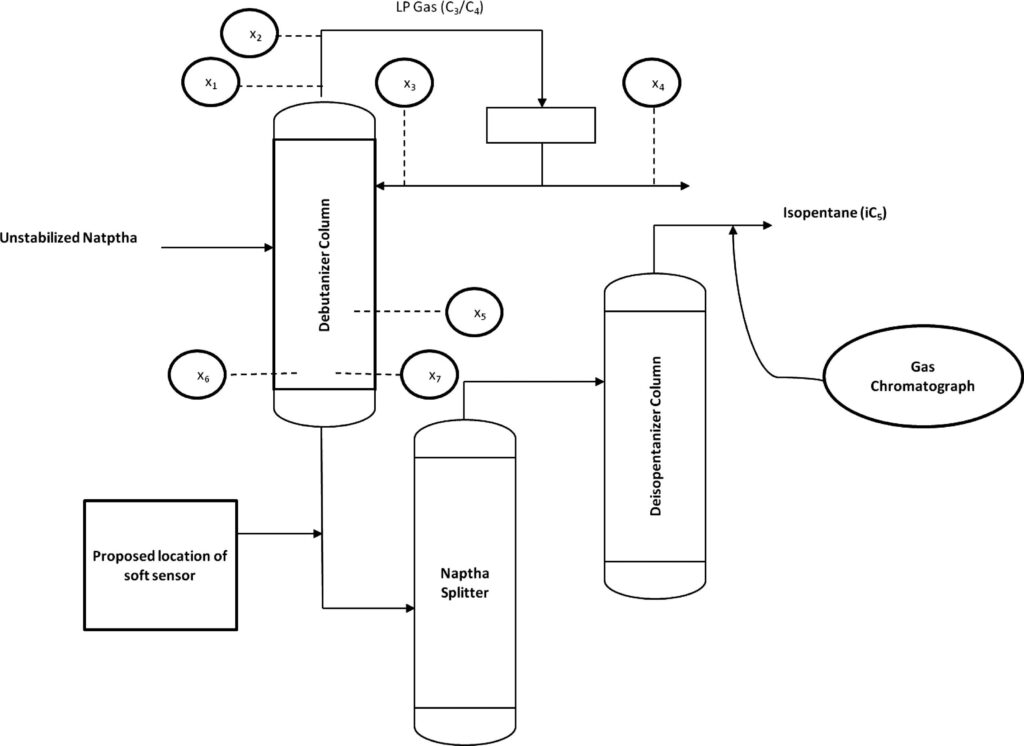
コチラのGitHubページで入手できる「debutanizer_data.csv」を利用します。
脱ブタン塔のプロセスデータであり、プロセスフローは上図の通りです。
説明変数がx1〜x7の7個で、目的変数がyの1個、サンプル数は2394個です。
| 変数名 | 詳細 | 日本語訳 |
|---|---|---|
| x1 | Top Temperature | 塔頂温度 |
| x2 | Top pressure | 塔頂圧力 |
| x3 | Reflux flow | 還流流量 |
| x4 | Flow to next process | 次プロセスへの流量 |
| x5 | 6th tray Temperature | 6段目温度 |
| x6 | Bottom Temperature1 | 塔底温度1 |
| x7 | Bottom Temperature2 | 塔底温度2 |
| y | Butane(C4) content in the debutanizer column bottom | 塔底におけるブタン含有量 |
データの読み込み
「debutanizer_data.csv」と同じフォルダに、「shap_debutanizer.ipynb」というファイルを作成しましょう。
下記のコードでライブラリのインポートと、データの読み込みを行います。
簡単なデータの前処理として、目的変数yの測定時間を考慮し、5行だけずらしておきましょう。
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.figure as figure
import japanize_matplotlib
from scipy.stats import norm
import seaborn as sns
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error, r2_score
from sklearn.ensemble import RandomForestRegressor
from sklearn.inspection import permutation_importance, PartialDependenceDisplay, partial_dependence
import shap
#pdfで保存する
from matplotlib.backends.backend_pdf import PdfPages
#脱ブタン塔のプロセスデータを読み込む
df = pd.read_csv('debutanizer_data.csv')
# 目的変数の測定時間を考慮
df['y'] = df['y'].shift(5)
#yがnanとなる期間のデータを削除
df = df.dropna()
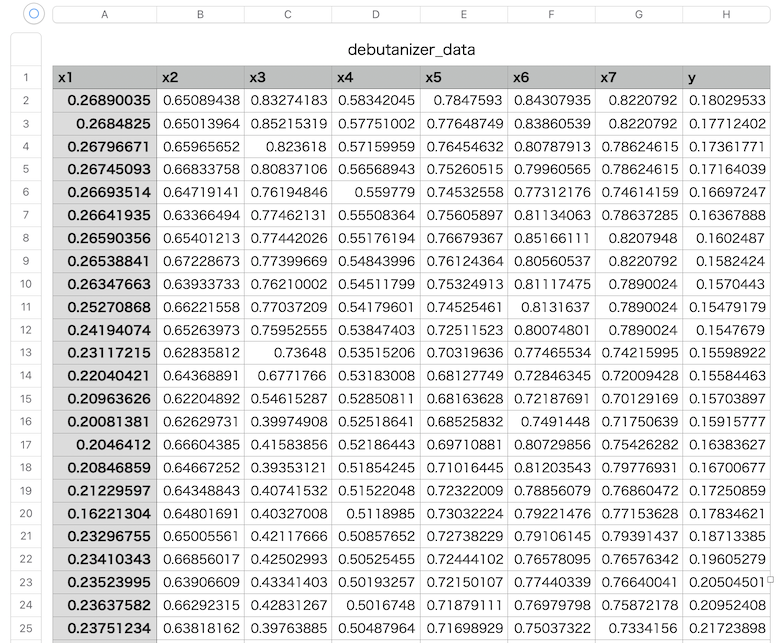
データの可視化
プロセスデータの中身を確認するため、データを可視化してみましょう。
トレンドデータ
プロセスデータは時系列データですので、まずトレンドグラフを確認します。
下記のコードで説明変数xと目的変数yを比較したトレンドグラフを作成できます。
#pdfで保存するためpdfインスタンスを作成
pdf = PdfPages('trend_debutanizer.pdf')
#トレンドデータを可視化
for col in df.columns:
if col == 'y':
continue
else:
fig, ax1 =plt.subplots(figsize=(14,5))
ax2 = ax1.twinx()
ax1.plot(df[col])
ax1.set_ylabel(col)
ax2.plot(df['y'], color='red')
ax2.set_ylabel('y')
plt.grid(False)
h1, l1 = ax1.get_legend_handles_labels()
h2, l2 = ax2.get_legend_handles_labels()
ax1.legend(h1+h2, l1+l2, loc='best')
plt.show()
# グラフを保存
fig.savefig(f'{col}_trend.png', dpi=150)
pdf.savefig(fig)
plt.close(fig)
#close処理
pdf.close()
代表例として、x5とyのトレンドグラフを見てみましょう。
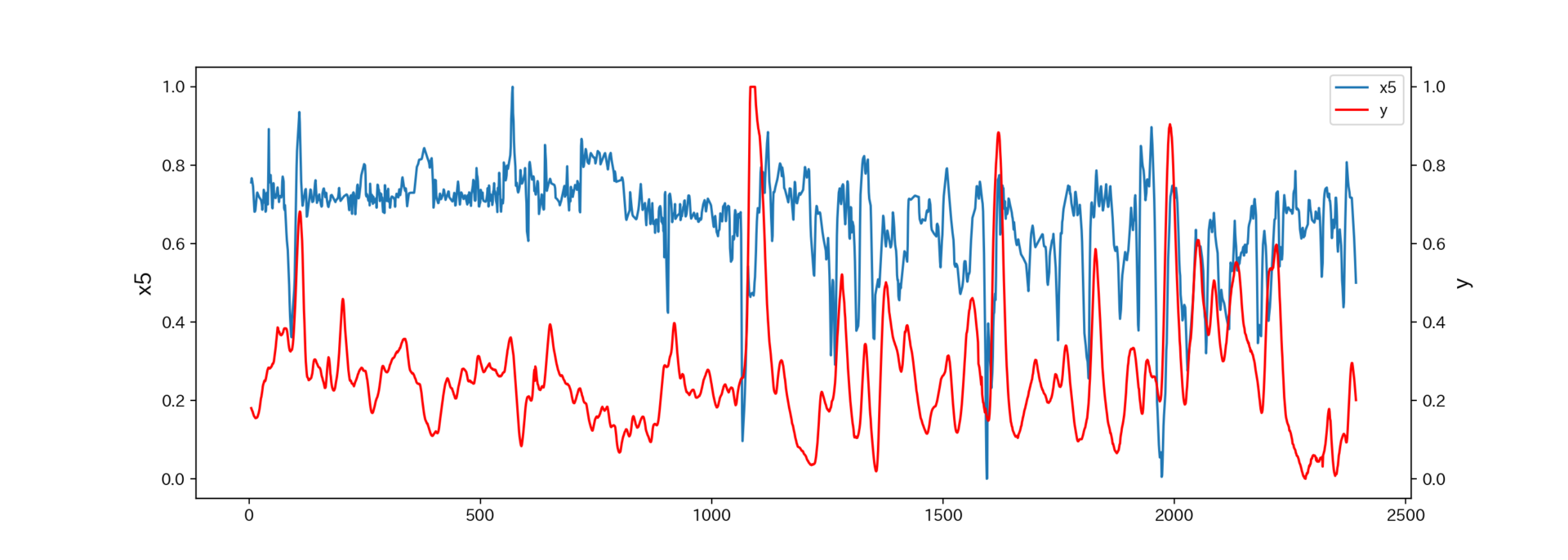
X5(6段目温度)が急低下する際に、塔底の低沸点分(ブタン)が急上昇していることがわかります。
ただし、数プロット分yが遅れて変動しているようです。
よって後ほど、この時間遅れを補正します。
ヒストグラム
続いて、ヒストグラムを作成してデータの分布を確認します。
#pdfで保存するためpdfインスタンスを作成
pdf = PdfPages('histogram_debutanizer.pdf')
# 列ごとにヒストグラムを作成
for col in df.columns:
# スタイルを変更(背景色を白、軸名の色を黒に設定)
plt.style.use('default')
# グラフの設定
fig, ax = plt.subplots(figsize=(8, 5))
# ヒストグラムのbinの数を計算(スタージェスの公式)
num_bins = int(np.log2(df[col].shape[0]) + 1)
# ヒストグラムの表示(density=Trueで密度表示)
ax.hist(df[col], bins=num_bins, density=True, alpha=0.7, label='Histogram')
# 正規分布のパラメータの推定
mu, sigma = norm.fit(df[col])
# 正規分布曲線のx値の範囲を決定
x = np.linspace(df[col].min(), df[col].max(), 100)
# 正規分布曲線の描画
ax.plot(x, norm.pdf(x, mu, sigma), 'r-', label='Normal Distribution')
ax.set_xlabel(f'{col}_value')
ax.set_ylabel('Frequency')
ax.legend()
plt.show()
# グラフを保存
fig.savefig(f'{col}_histogram_sturges.png', dpi=200)
pdf.savefig(fig)
plt.close(fig)
#close処理
pdf.close()
代表例として、x2とx3のヒストグラムを見てみましょう。
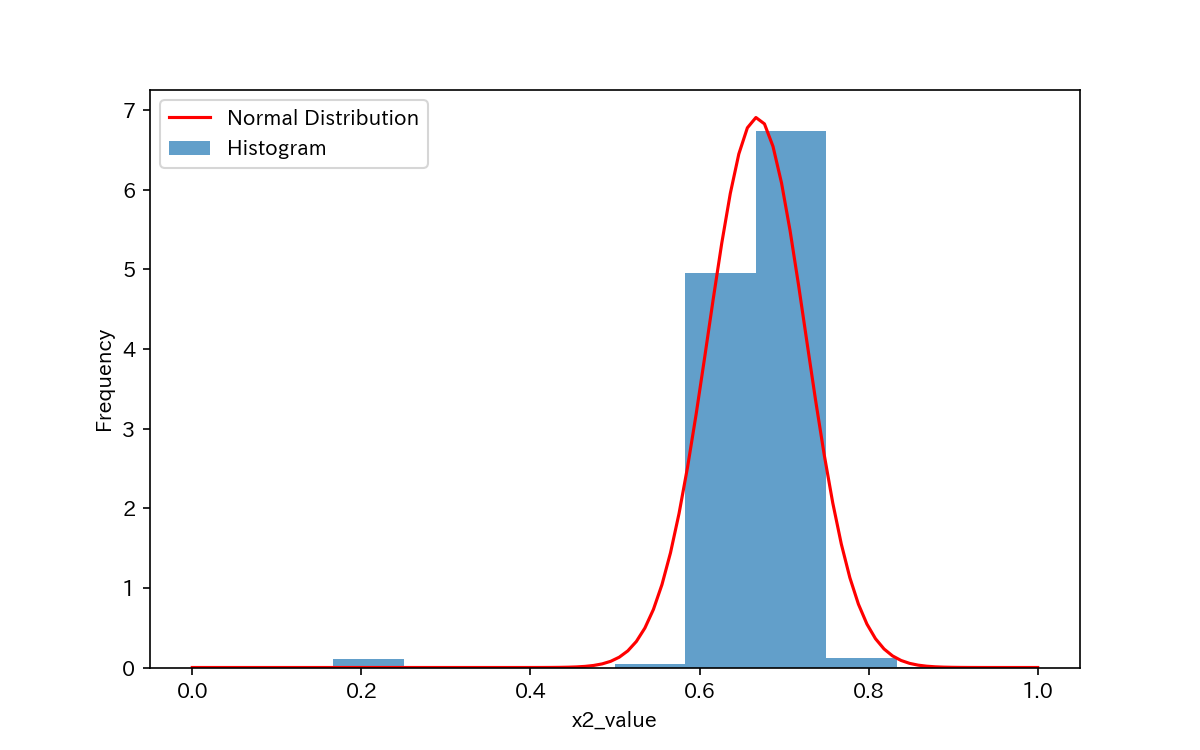
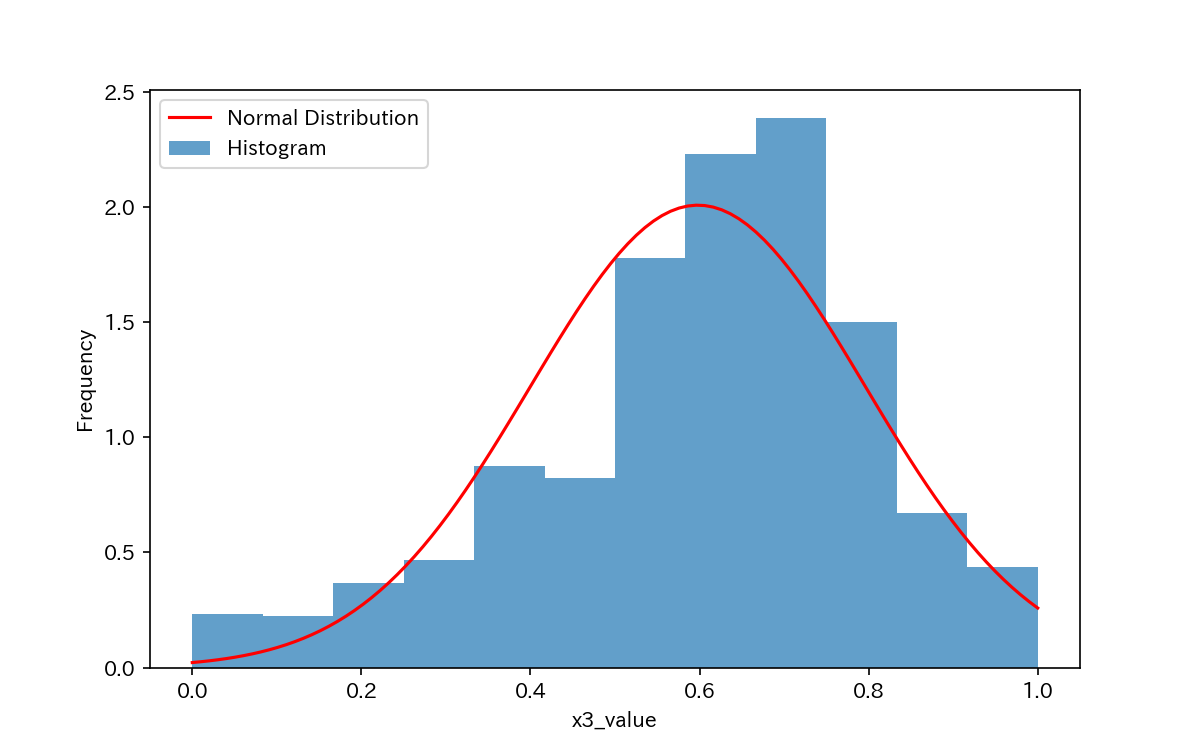
x3は正規分布に近いデータ分布をしていますが、x2は分布がシャープになっています。
よく見るとx2には外れ値のようなものがありますね。
ヒストグラムの描き方やビンの数の決定方法については、下記記事で詳しく解説しています。
-

-
【python】ヒストグラムの作成方法(スタージェスの公式)
続きを見る
散布図
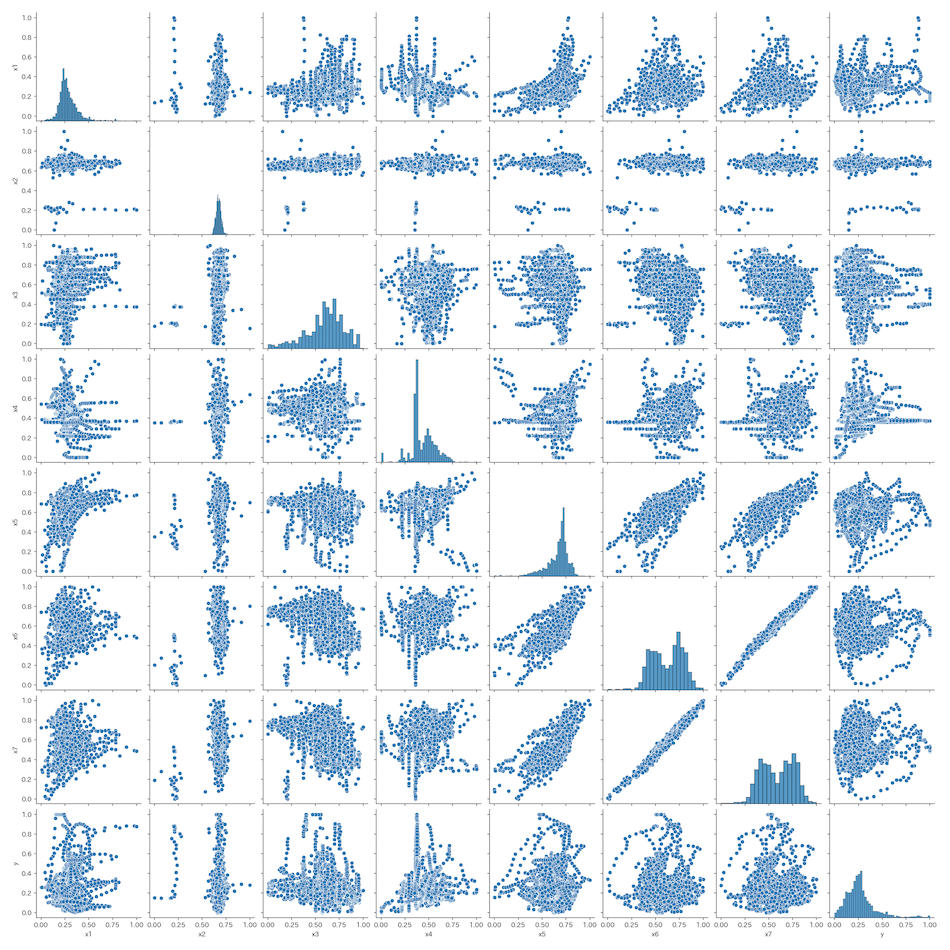
変数同士の散布図をseabornのpairplotで確認します。
相関がありそうなデータを見た目で確認できます。
#各変数同士の散布図を確認
sns.pairplot(df)
plt.savefig('pairplot_debutanizer.png', dpi=150)
相関係数
相関行列を作成して、変数間の相関係数を確認しましょう。
相関行列をcsvファイルで保存し、目的変数yに対する相関係数は棒グラフで可視化します。
#相関行列を確認
df_corr = df.corr()
df_corr.to_csv('df_corr_debutanizer.csv')
#yに対する相関係数をグラフ化
df_corr_sort = abs(df_corr).sort_values('y')
fig, ax = plt.subplots()
ax.barh(df_corr_sort.index[:-1], df_corr_sort['y'][:-1])
ax.set(xlabel='| 相関係数r |')
fig.suptitle('目的変数yに対する相関係数(r)')
fig.savefig('correlation_debutanizer.png', dpi=150)
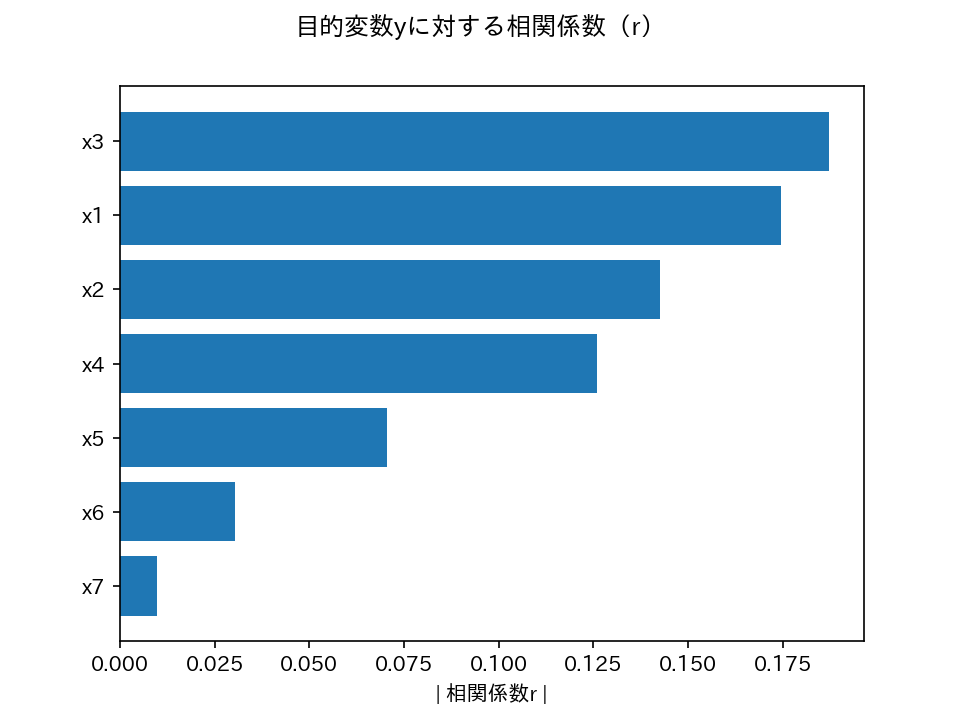
上図から、x3、x1、x2、x4、x5の順番で、yとの相関係数(の絶対値)が大きいことがわかりました。
回帰モデルの作成
データを確認した後は、回帰モデルを作成していきます。
機械学習を用いた回帰モデルとして、本記事ではランダムフォレストを扱います。
時間遅れ変数の作成
時間遅れ変数の作成や変数選択は、本記事の主題ではないため簡単な処理のみとします。
#説明変数と目的変数にわける
X = df.iloc[:, :-1]
y = df['y']
#時間遅れ変数を作成
delay_number = 18
X_with_delays = pd.DataFrame()
for col in X.columns:
col_name = f"{col}_delay_{delay_number}"
X_with_delays[col_name] = X[col].shift(delay_number)
# 時間遅れ変数とyのデータフレームを作成
X_with_delays['y'] = y
X_with_delays = X_with_delays.dropna()
# 目的変数と説明変数に分割
y = X_with_delays['y']
X = X_with_delays.iloc[:, :-1]
相関係数の再確認
時間遅れ変数と目的変数yとの相関係数を確認しておきましょう。
# 時間遅れ変数を含むデータフレームの相関行列を計算
X_with_delays_corr = X_with_delays.corr()
# 相関行列をCSVファイルに保存
X_with_delays_corr.to_csv('X_with_delays_corr_debutanizer.csv')
# yに対する相関係数をグラフ化
X_with_delays_corr_sort = abs(X_with_delays_corr).sort_values('y')
fig, ax = plt.subplots()
ax.barh(X_with_delays_corr_sort.index[:-1], X_with_delays_corr_sort['y'][:-1])
ax.set(xlabel='| 相関係数r |')
fig.suptitle('目的変数yに対する相関係数(r)')
# 左側にスペースを空ける
plt.subplots_adjust(left=0.3)
# グラフを保存
fig.savefig('delays_correlation_debutanizer.png', dpi=150)
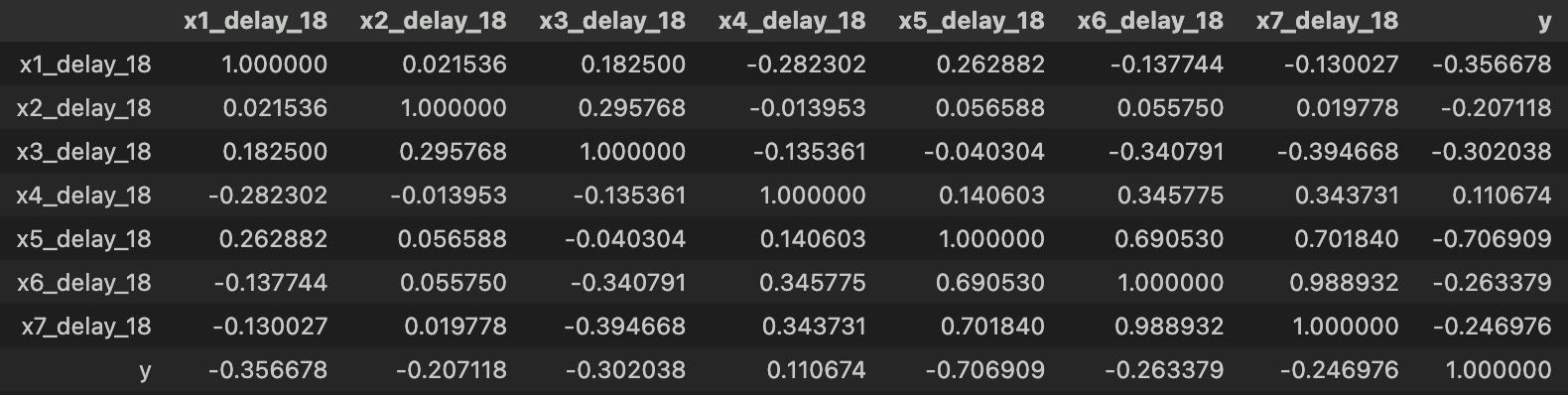
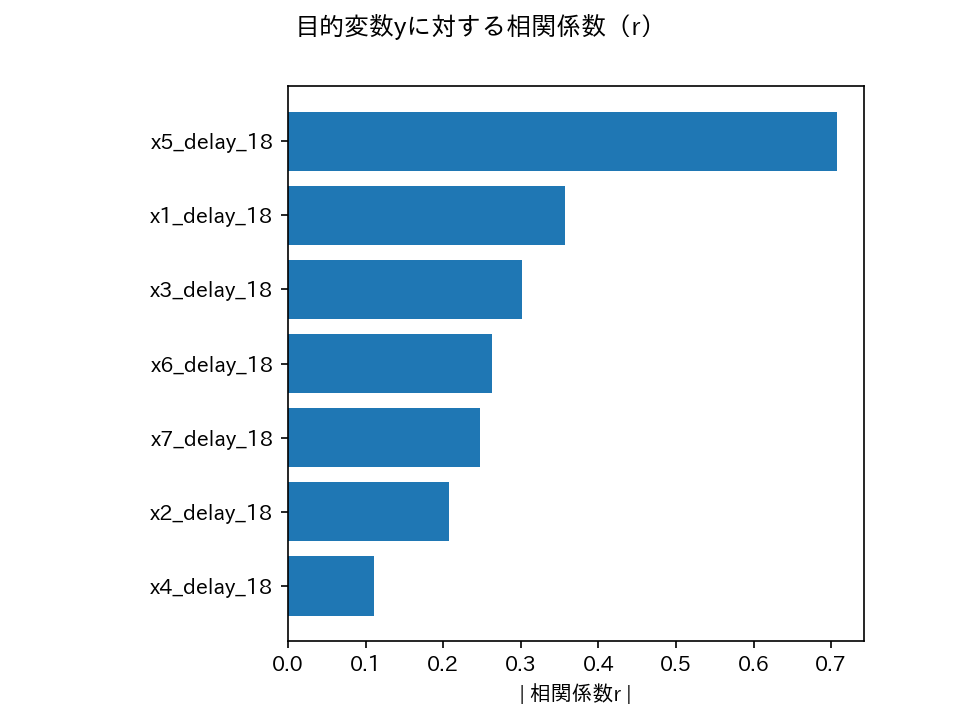
時間遅れ変数とyの相関係数(の絶対値)は、生データの相関係数に比べて全体的に大きくなりました。
特にx5では相関係数(の絶対値)が顕著に大きくなっており、プロセスデータにおける時間遅れ変数の重要性がわかります。
ランダムフォレスト(RF)
本記事では、予測精度は本題ではないためランダムフォレストで回帰モデルを作成していきます。
ハイパーパラメータ決定の際も、クロスバリデーションなどの方法は特に使用していません。
#学習データとテストデータに分割 X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.4, shuffle=False) #ランダムフォレスト rf = RandomForestRegressor(n_estimators=300, max_depth=5, max_features=0.8, random_state=42) #ランダムフォレストのモデルを作成 rf.fit(X_train, y_train)
プロセスデータは時系列データなので、学習データとテストデータに分割する際にshuffle=Falseとしました。
予測精度(RMSE、R2)
RMSEと決定係数R2を確認します。
下記のコードでは、得られたRMSEとR2をcsvファイルに保存します。
# 学習データのおける予測値を算出
y_train_pred_rf = rf.predict(X_train)
# 評価指標の出力(RMSE、R2)
train_rmse = mean_squared_error(y_train, y_train_pred_rf, squared=False)
train_r2 = r2_score(y_train, y_train_pred_rf)
print(f'RMSE(学習):{train_rmse}')
print(f'R2(学習):{train_r2}')
# テストデータのおける予測値を算出
y_test_pred_rf = rf.predict(X_test)
# 評価指標の出力(RMSE、R2)
test_rmse = mean_squared_error(y_test, y_test_pred_rf, squared=False)
test_r2 = r2_score(y_test, y_test_pred_rf)
print(f'RMSE(テスト):{test_rmse}')
print(f'R2(テスト):{test_r2}')
# RMSEとR2をエクセルファイルに保存
results_df = pd.DataFrame({'RMSE': [train_rmse, test_rmse], 'R2': [train_r2, test_r2]}, index=['Train', 'Test'])
results_df.to_csv('results.csv')
| RMSE | R2 | |
| Train | 0.057 | 0.835 |
| Test | 0.127 | 0.520 |
実測値 v.s 推定値のプロット
RMSEやR2を見るだけではく、実測値と推定値のプロットも確認しましょう。
学習データ
# 実測値 vs. 推定値のプロット(学習データ)
plt.figure(figsize=figure.figaspect(1))
plt.scatter(y_train, y_train_pred_rf, c='blue') # 実測値 vs. 推定値プロット
# 実測値と推定値の最大値・最小値を取得
y_max = max(y_train.max(), y_train_pred_rf.max())
y_min = min(y_train.min(), y_train_pred_rf.min())
# 対角線を作成
margin = 0.05 * (y_max - y_min) # 対角線の端点を、最大値・最小値から5%ずつ離す
plt.plot([y_min - margin, y_max + margin], [y_min - margin, y_max + margin], 'k-')
# x 軸・y 軸の範囲を設定
plt.ylim(y_min - margin, y_max + margin)
plt.xlim(y_min - margin, y_max + margin)
# x 軸・y 軸の名前を設定
plt.xlabel('actual y')
plt.ylabel('estimated y')
# グラフ内にテキストを追加
plt.text(0.05, 0.95, 'Training Data_rf', ha='left', va='top', transform=plt.gca().transAxes)
# グラフをpng形式で保存
plt.savefig('actual_vs_estimated_train_rf.png', dpi=300)
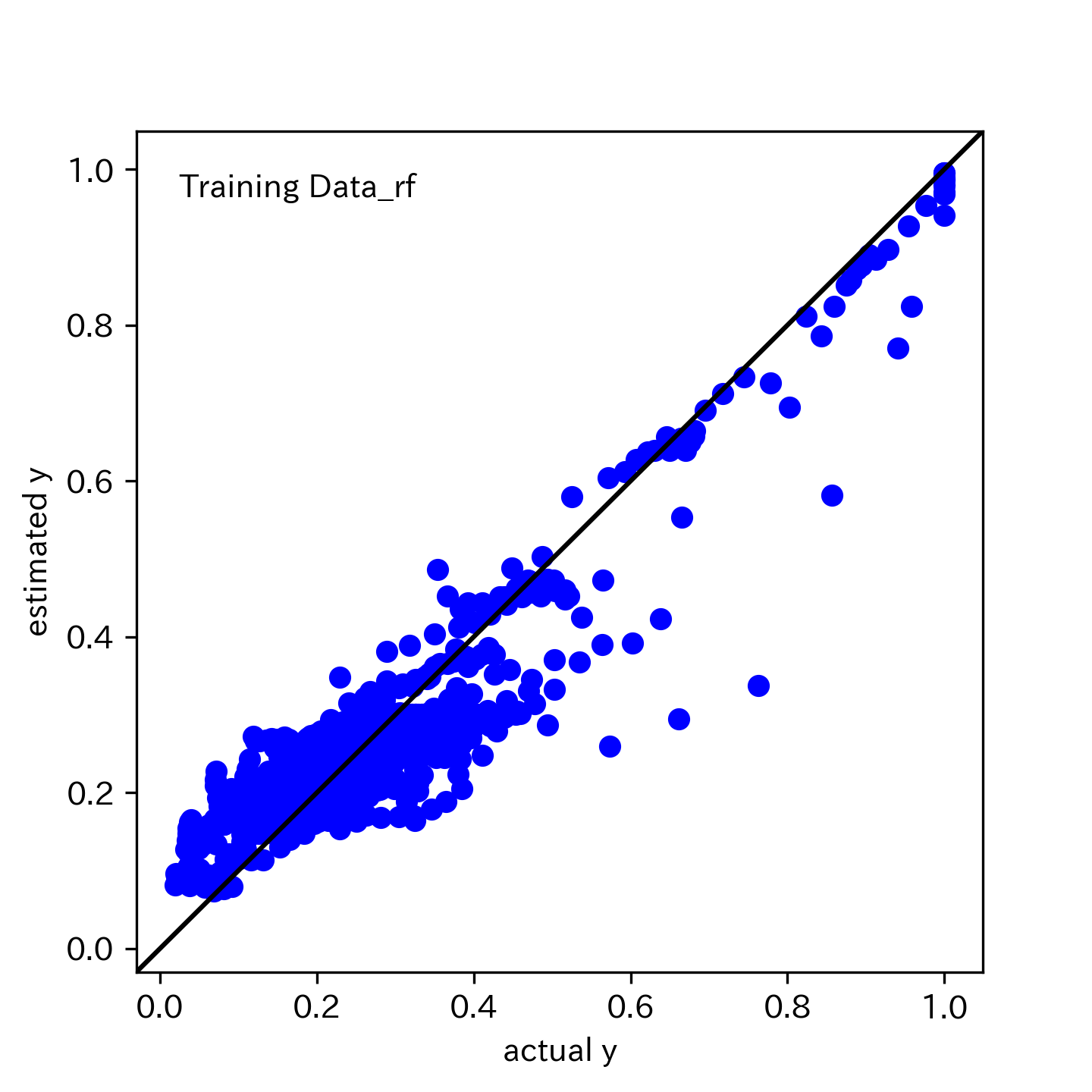
テストデータ
# 実測値 vs. 推定値のプロット(テストデータ)
plt.figure(figsize=figure.figaspect(1))
plt.scatter(y_test, y_test_pred_rf, c='blue') # 実測値 vs. 推定値プロット
# 実測値と推定値の最大値・最小値を取得
y_max = max(y_test.max(), y_test_pred_rf.max())
y_min = min(y_test.min(), y_test_pred_rf.min())
# 対角線を作成
margin = 0.05 * (y_max - y_min) # 対角線の端点を、最大値・最小値から5%ずつ離す
plt.plot([y_min - margin, y_max + margin], [y_min - margin, y_max + margin], 'k-')
# x 軸・y 軸の範囲を設定
plt.ylim(y_min - margin, y_max + margin)
plt.xlim(y_min - margin, y_max + margin)
# x 軸・y 軸の名前を設定
plt.xlabel('actual y')
plt.ylabel('estimated y')
# グラフ内にテキストを追加
plt.text(0.10, 0.05, 'Test Data_rf', ha='left', va='top', transform=plt.gca().transAxes)
# グラフをpng形式で保存
plt.savefig('actual_vs_estimated_test_rf.png', dpi=300)
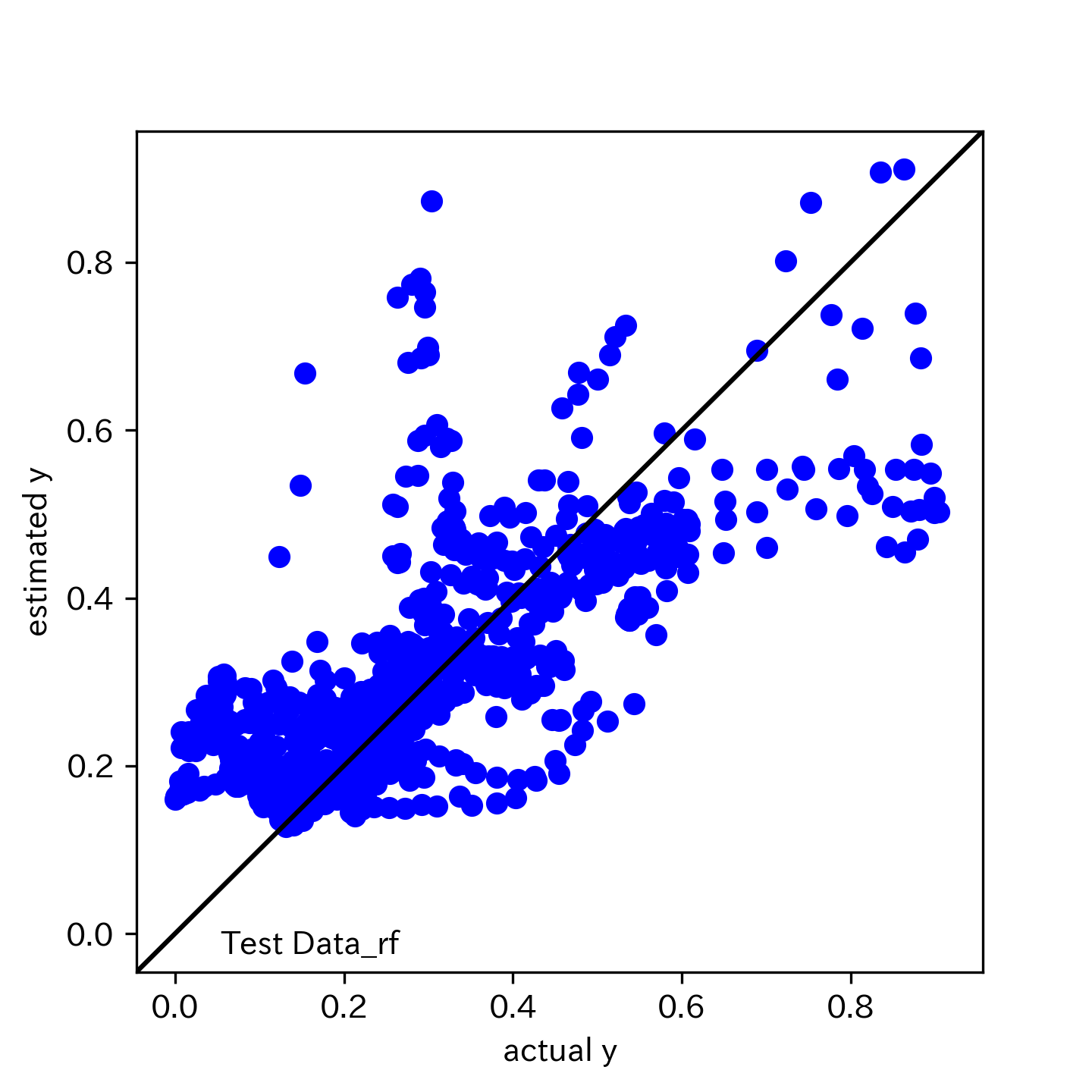
【実践】機械学習の解釈手法
やっと機械学習の解釈手法を用いる準備ができました。
PFI、PD、ICE、SHAPといった機械学習の解釈手法を、プロセスデータに適用してみましょう。
特徴量の重要度(PFI)
# 特徴量の重要度を確認(PFI)※テストデータ
pfi = permutation_importance(
estimator=rf,
X=X_test,
y=y_test,
scoring='neg_root_mean_squared_error',
n_repeats=5,
n_jobs=-1,
)
# テストデータのPFIをデータフレームに格納
df_pfi = pd.DataFrame(
data={'var_name': X_test.columns, 'importance': pfi['importances_mean']}
).sort_values('importance')
# 特徴量の重要度(PFI)をグラフ化
fig, ax = plt.subplots()
ax.barh(df_pfi['var_name'], df_pfi['importance'])
ax.set(xlabel='differences')
fig.suptitle('Permutationによる特徴量の重要度(difference)')
# 左側にスペースを空ける
plt.subplots_adjust(left=0.3)
# グラフを保存
fig.savefig('PFI_graph_debutanaizer.png', dpi=150)
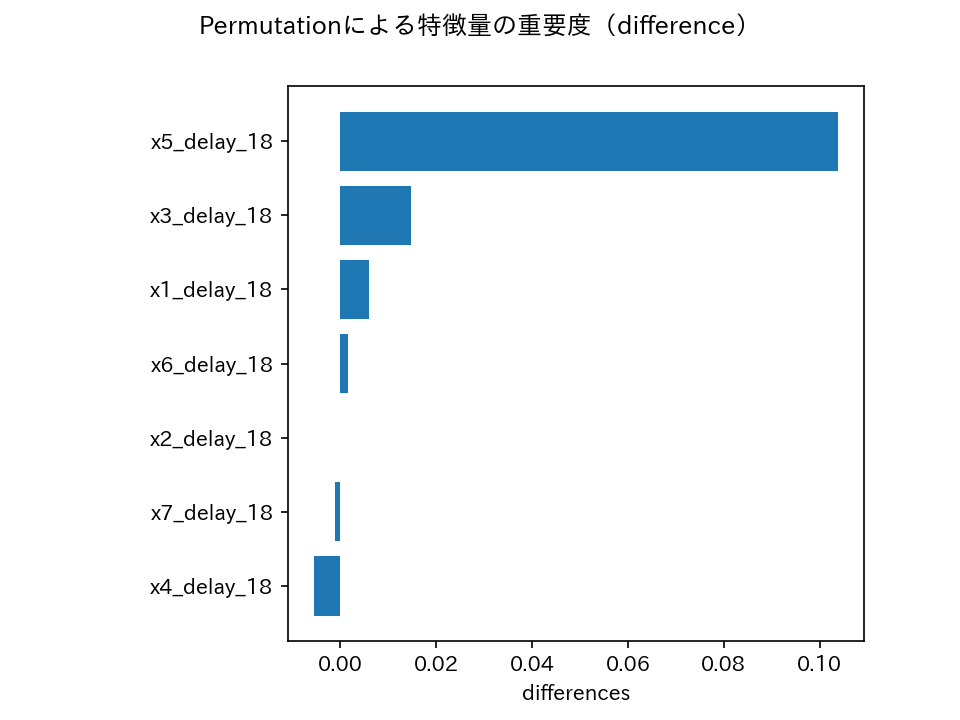
特徴量の重要度(PFI)は、概ね相関係数の絶対値と同じような順番となりました。
やはりx5の時間遅れ変数(x5_delay_18)が効いてそうです。
特徴量と予測値の平均的な関係(PD)
特徴量の重要度(PFI)が大きい上位4変数のPDをグラフ化します。
# 特徴量の重要度(PFI)が大きい上位4変数のPDをグラフ化
for col in df_pfi['var_name'][-4:]:
fig, ax = plt.subplots(figsize=(8, 6))
PartialDependenceDisplay.from_estimator(
estimator=rf,
X=X_test,
features=[col], # PDを計算したい特徴量
kind="average", # PDは"average", ICEは"individual"、両方は"both"
ax=ax
)
fig.suptitle(f'{col}のPartial Dependence Plot')
fig.savefig(f'{col}_PD_graph.png', dpi=150)
plt.close(fig)
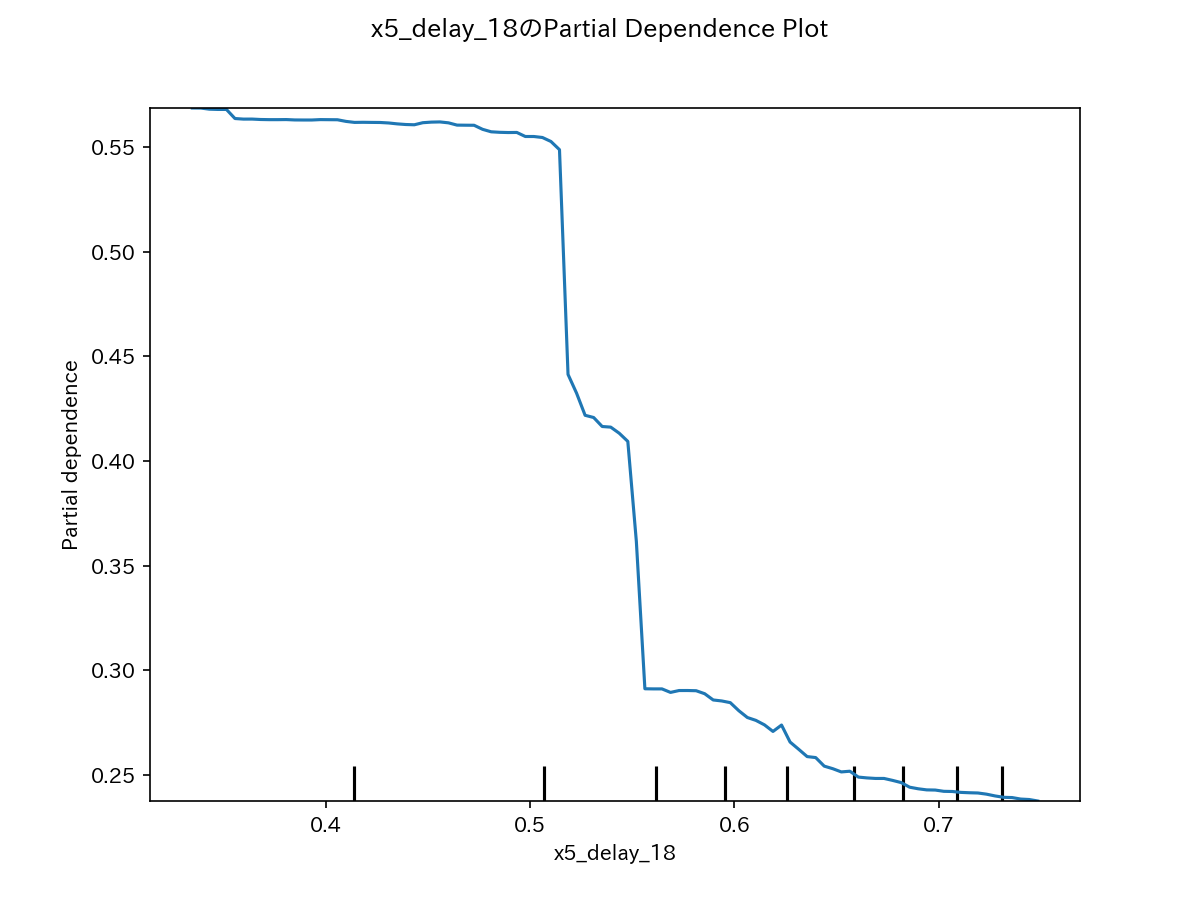
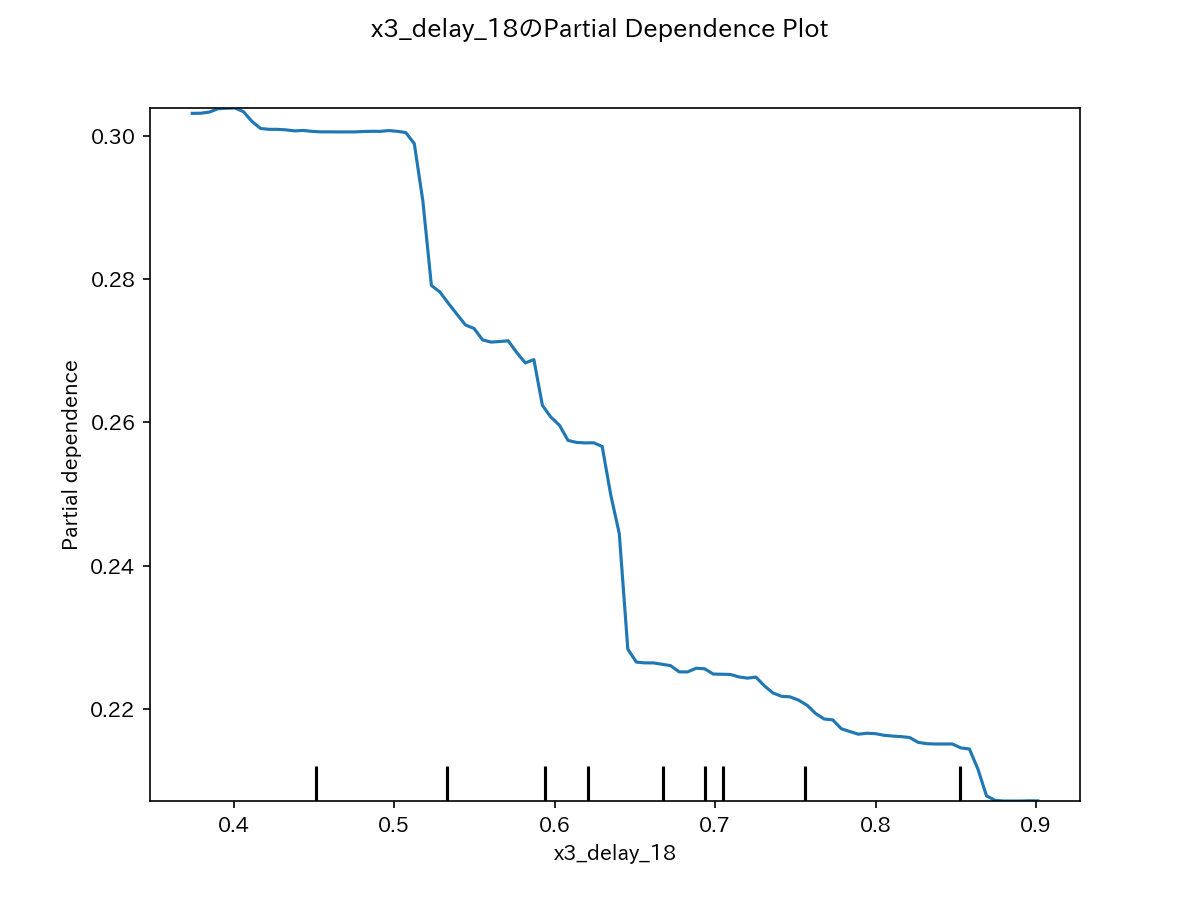
代表例として、上位2変数のPDグラフを示します。
x5、x3ともに大きくしていくと、yが小さくなっていくことを示しています。
これは、前述の相関係数がマイナスになっていたことと一致します。
インスタンス毎の特徴量と予測値の関係(ICE)
PDと同様に、特徴量の重要度(PFI)が大きい上位4変数のICEをグラフ化します。
# 特徴量の重要度(PFI)が大きい上位4変数のICEを可視化
for col in df_pfi['var_name'][-4:]:
fig, ax = plt.subplots(figsize=(8, 6))
PartialDependenceDisplay.from_estimator(
estimator=rf,
X=X_test,
features=[col], # PDを計算したい特徴量
kind="both", # PDは"average", ICEは"individual"、両方は"both"
ax=ax
)
fig.suptitle(f'{col}のICE Plot')
# グラフをpngファイルに保存
fig.savefig(f'{col}_ICE_graph.png', dpi=150)
plt.close(fig)
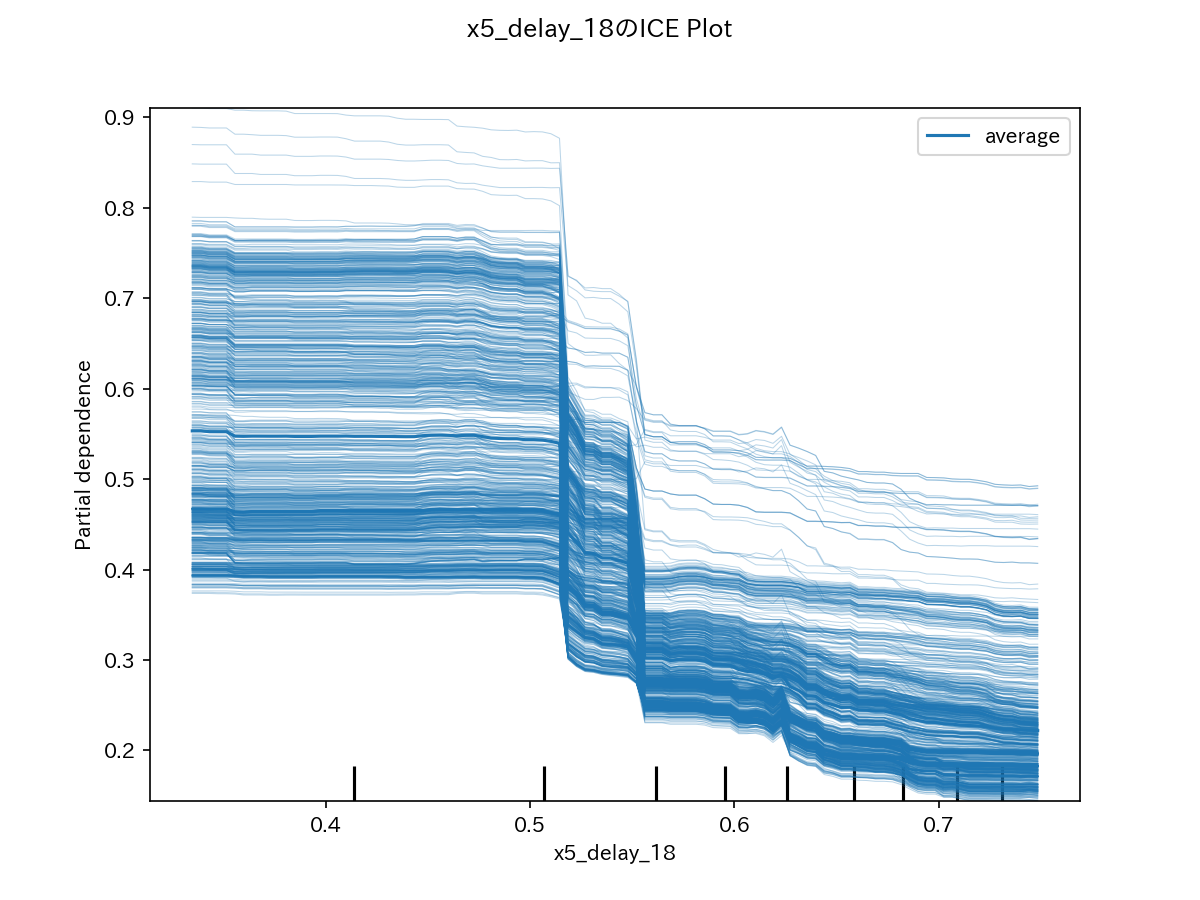
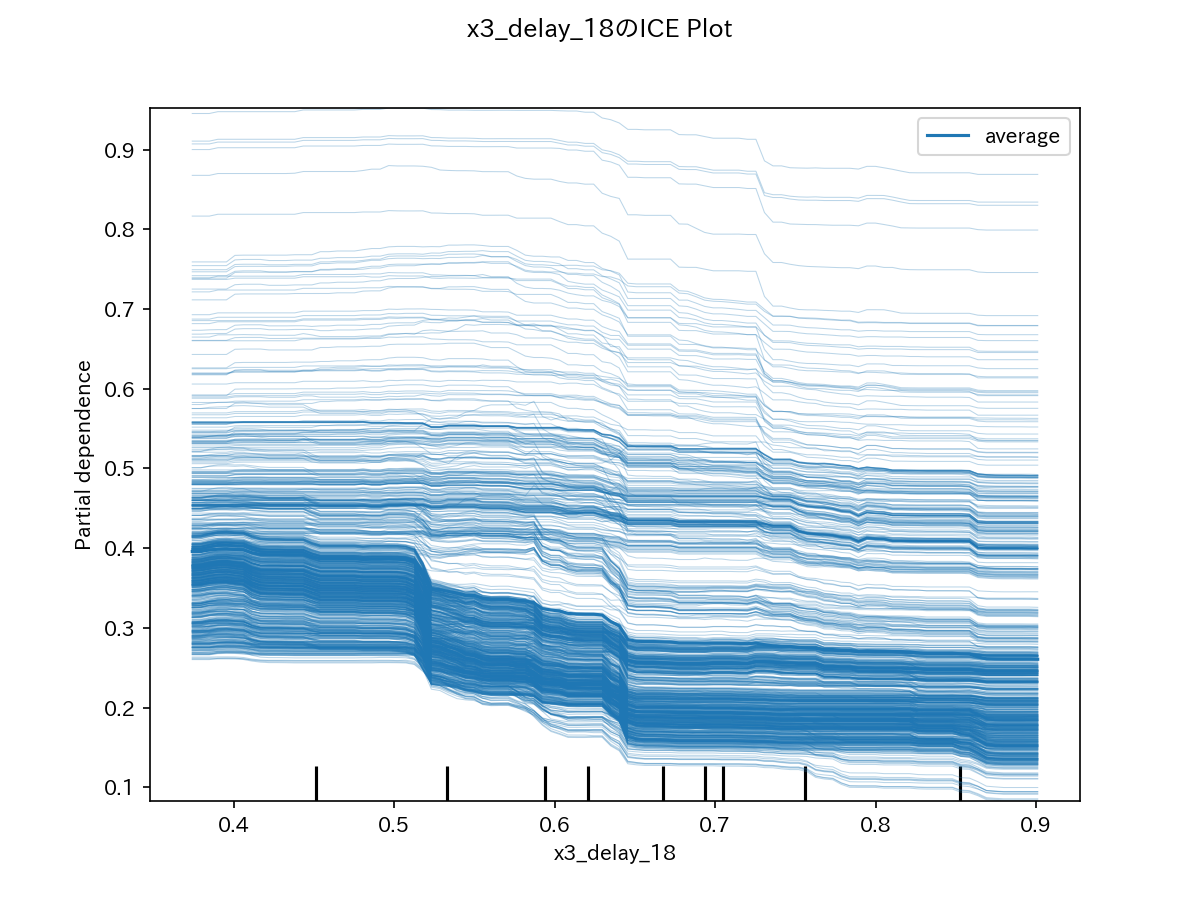
代表例として、上位2変数のICEグラフを示します。
下図の例では、すべてのインスタンスで同じような挙動を示しています。
特徴量ごとの貢献度・予測の理由(SHAP)
まず、shapライブラリを用いてSHAP値を計算します。
#SHAPを計算する
explainer = shap.TreeExplainer(
model=rf,
data=X_test,
feature_perturbation='interventional',#推奨
#check_additivity=False # 加法性チェックを無効にする
)
shap_values = explainer(X_test)
注意ポイント
最新のnumpyライブラリ(1.24.0以上)がインストールされているとエラーが出るようです。
numpy=1.23.0にダウングレードしたらエラーが出なくなりました。
【参考】github(shap)
各インスタンスの特徴量毎の貢献度
インスタンス0の特徴量ごと貢献度を可視化してみましょう。
shap.plots.waterfall(shap_values[0])
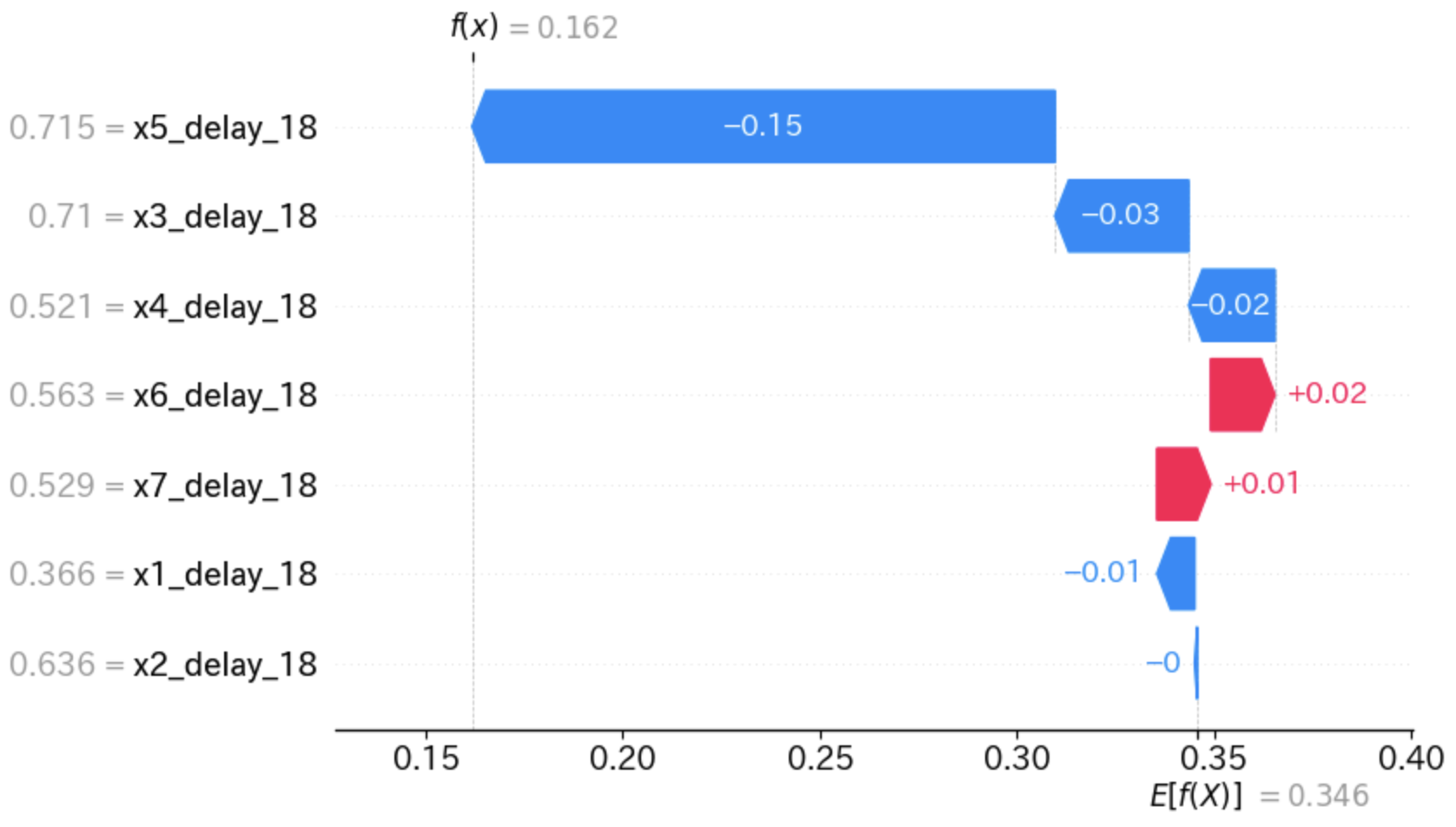
時系列データなので、最新のデータ(インスタンス)に対する貢献度も見てみましょう。
shap.plots.waterfall(shap_values[-1])
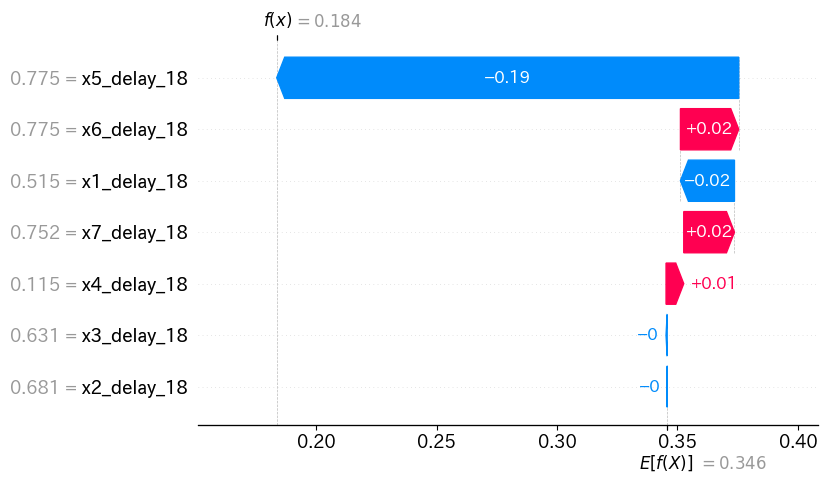
全インスタンスの平均的な貢献度(特徴量の重要度)
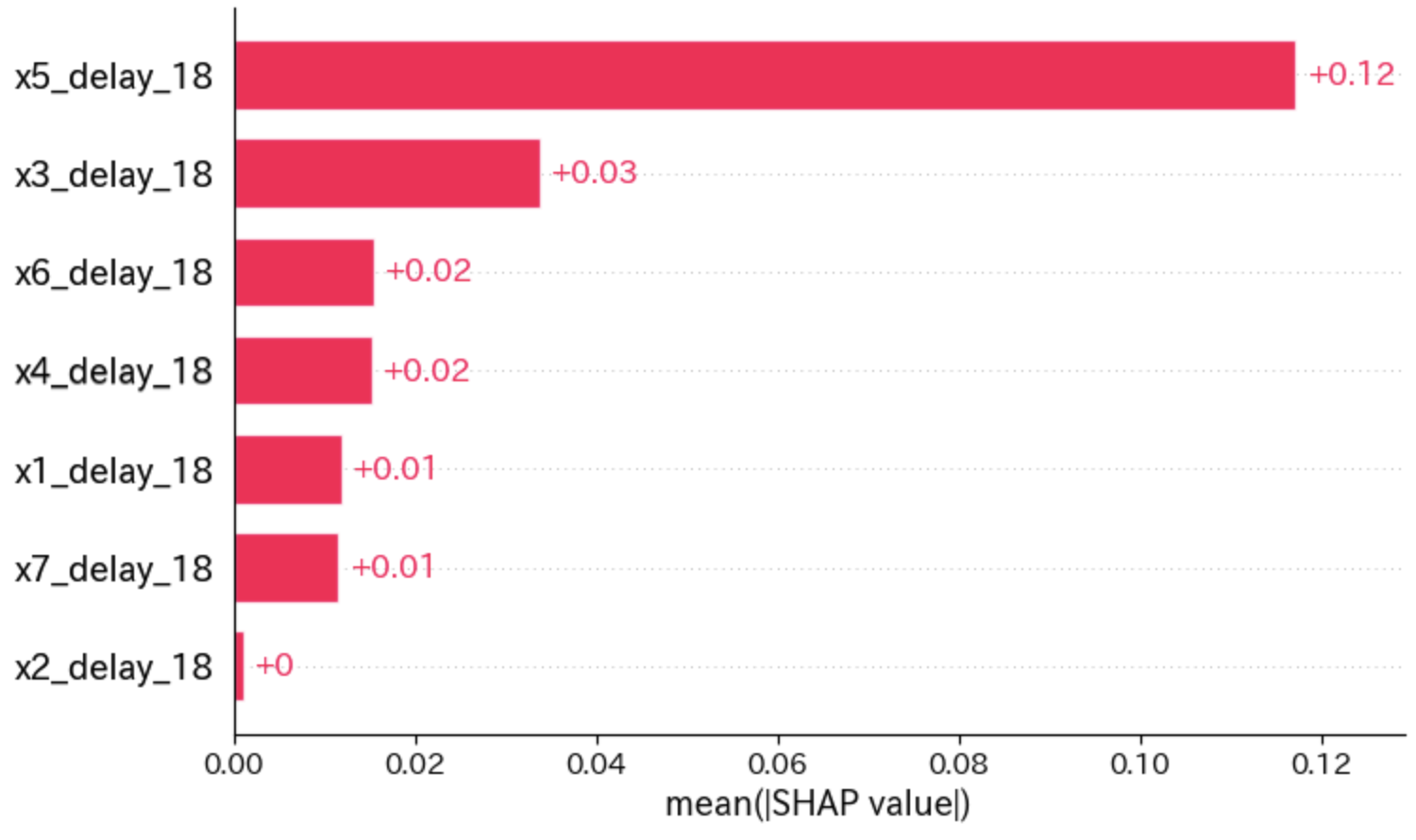
全インスタンスの平均的な貢献度を可視化してみます。
これを「特徴量の重要度」として解釈できます。
特徴量の重要度(PFI)と比較しても、上位2変数はx5とx3で同じですね。
shap.plots.bar(shap_values)
貢献度の分布
各インスタンスの「貢献度の分布」を確認しましょう。
平均的な貢献度だけではなく、貢献度の分布も必ず見るようにします。
shap.plots.beeswarm(shap_values)
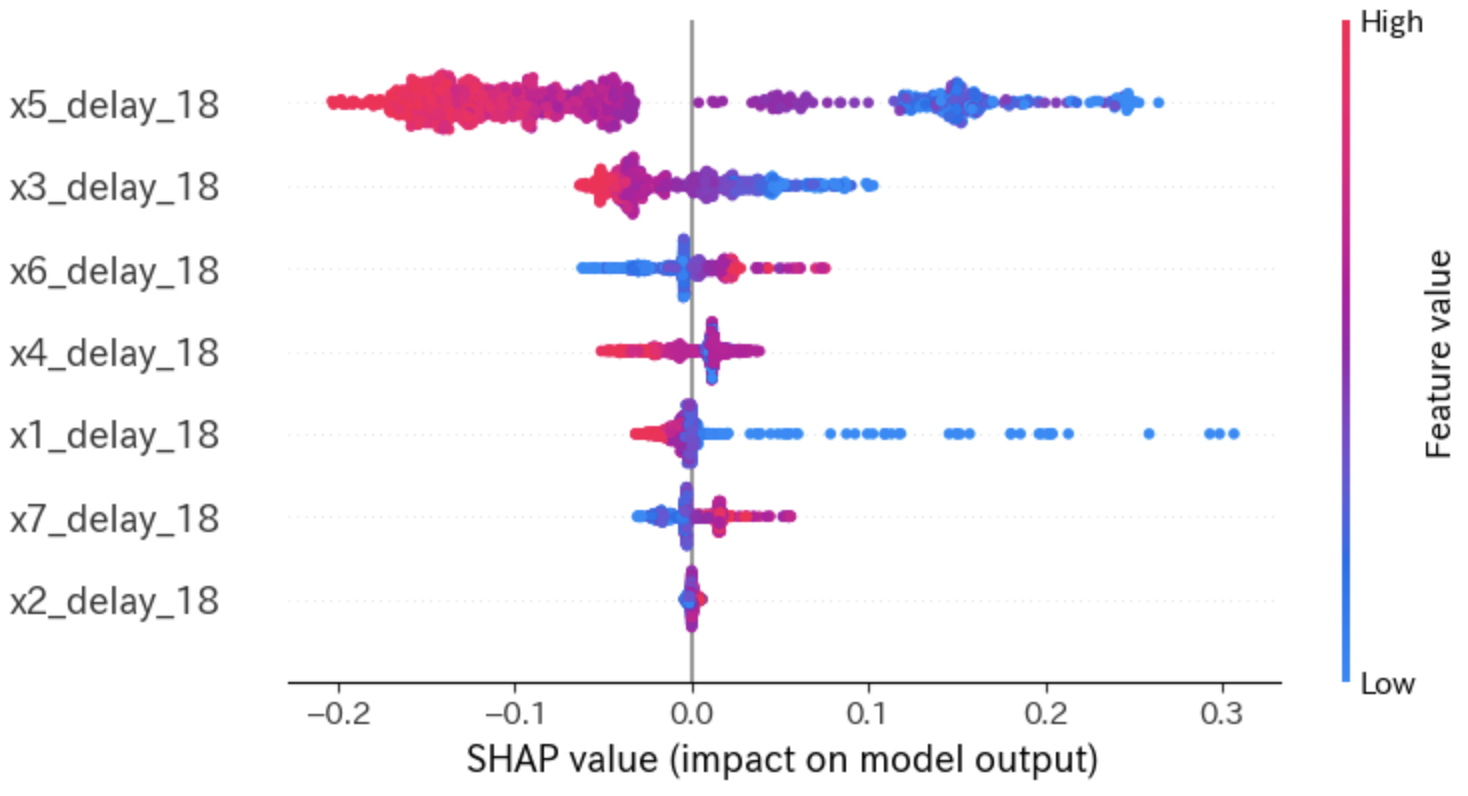
上図の第2縦軸は「特徴量の値(Feature value)」で色分けしています。
x5、x3共に、値が大きいときはSHAP値がマイナスであり、値が小さくなるとSHAP値がプラスになっていることがわかります。
特徴量と予測値の平均的な関係
SHAPでもPDのように、「特徴量と予測値の平均的な関係」を見ることができます
for col in X.columns:
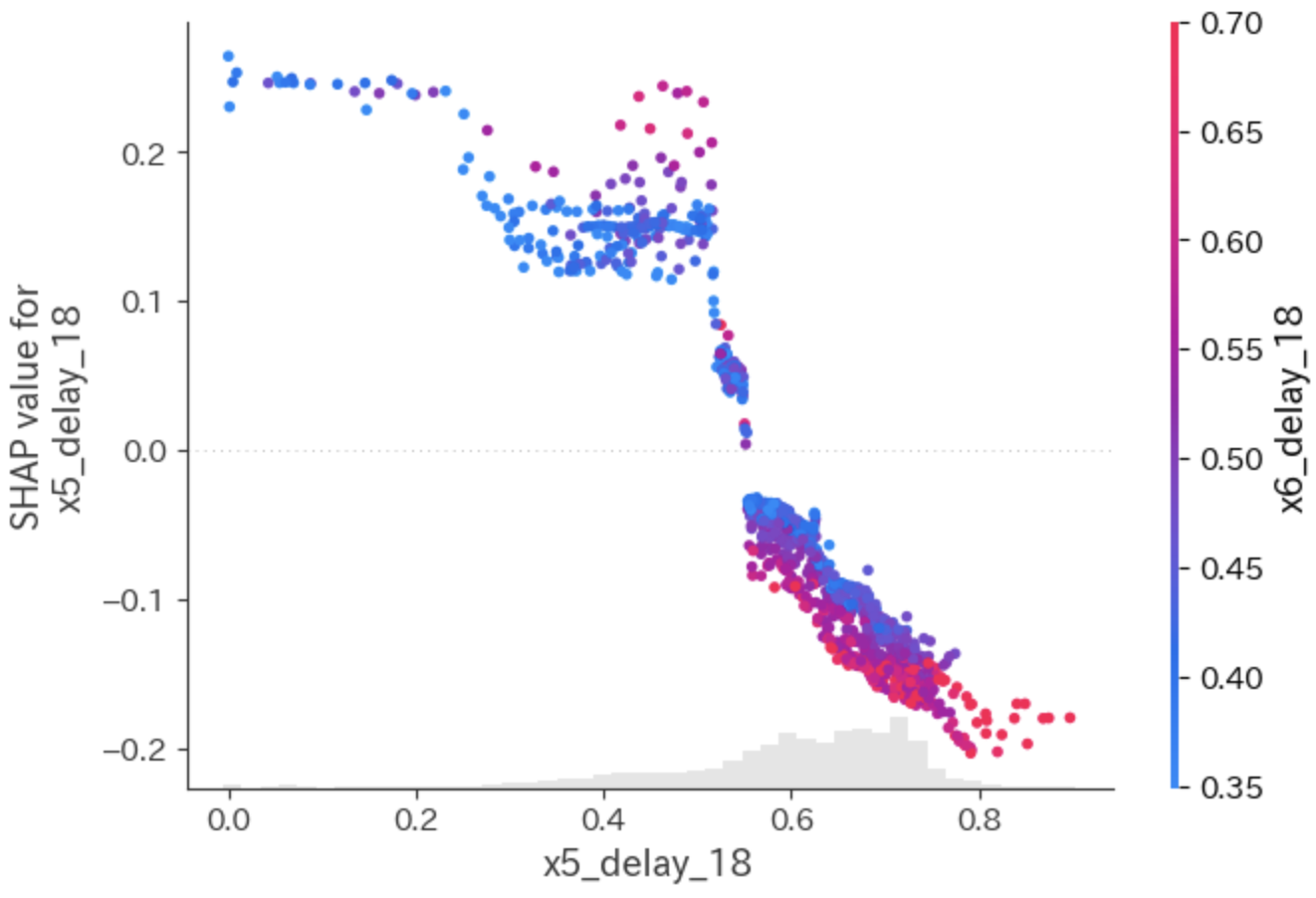
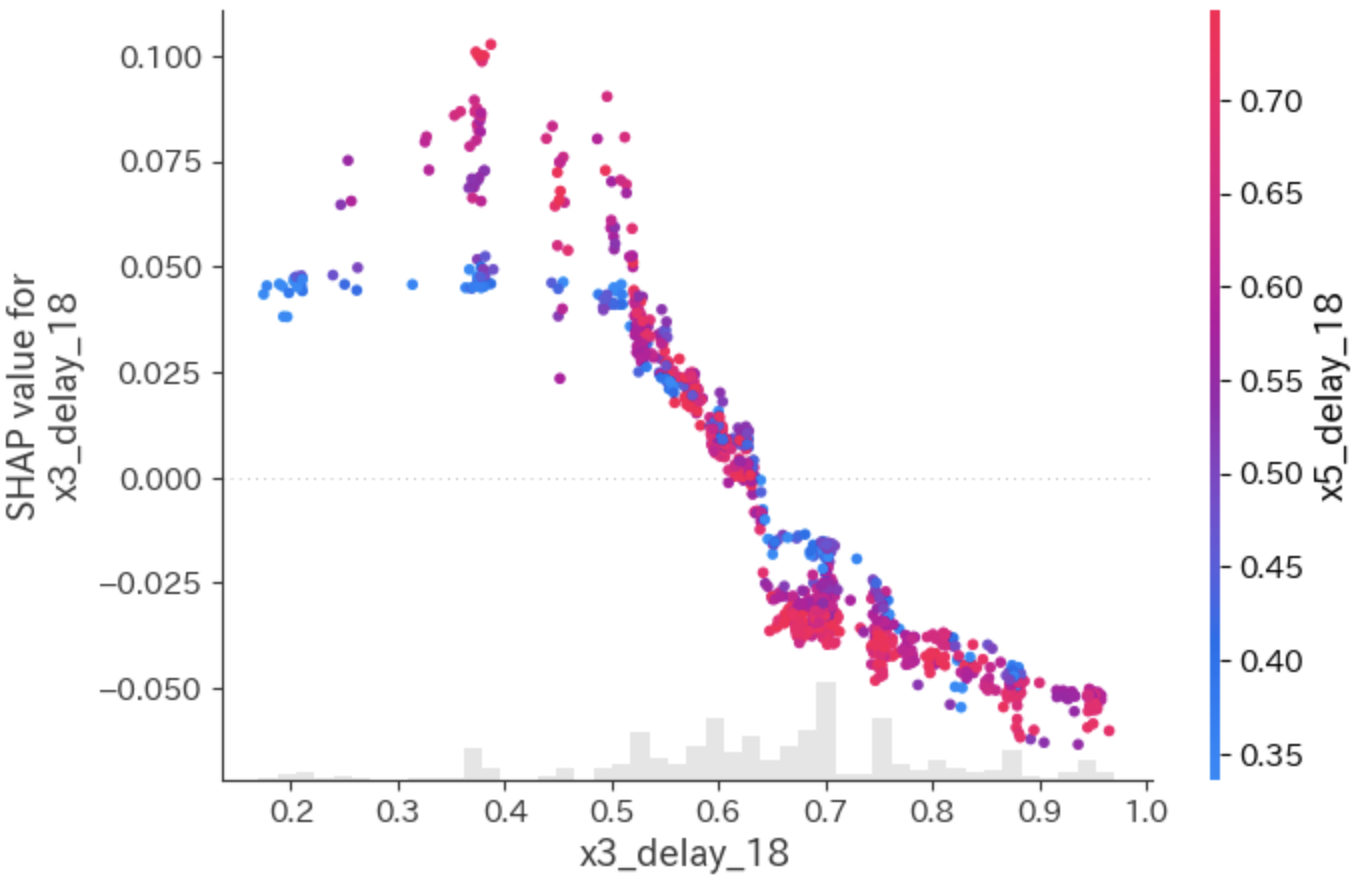
shap.plots.scatter(shap_values[:, col], color=shap_values)
代表例として、x5とx3のみ示します。
挙動はPDとよく似ていることがわかりますね。
x5は、0.5辺りのところで変曲点があるような図になっています。
また、colorにshap_valuesを指定すると、最も強い交互作用を持つ特徴量を自動で選択し、その値の高低で色づけしてくれます。
まとめ
機械学習の解釈手法であるPFI、PD、ICE、SHAPをプロセスデータに適用してみると、下記のことがわかりました。
まとめ
- 塔底におけるブタン含有量yを予測するモデルでは、x5(6段目温度)の時間遅れ変数(x5_delay_18)の重要度が高い。
- yとx5_delay_18の相関係数はマイナスであり、特徴量と予測値の平均的な関係(PD)においても、x5が大きくなるとyが小さくなることがわかる。
- SHAPを用いても上記2つと同じ解釈結果が得られる。
参考文献
機械学習を解釈する技術〜予測力と説明力を両立する実践テクニック(森下光之助著)
本記事は、上記の書籍を参考に書きました。
とても読みやすくて実用的なので、データ解析に取り組む方にオススメです。


