どうも。こんにちは。
ケミカルエンジニアのこーしです。
本日は、「ラグ特徴量(時間遅れ変数)による予測精度向上」についてわかりやすく解説します。
時系列データでは、目的変数yを予測する際にラグ特徴量(時間遅れ変数)を説明変数Xにすることで予測精度の向上が見込まれます。
そこで本記事では、目的変数yと最も相関係数が大きくなるラグ特徴量(時間遅れ変数)を探索した後、それらのラグ特徴量を用いて予測精度が向上するかを確認します。
本記事の内容
・最終成果物(Pythonコード)
・サンプルデータの入手
・PLSの実行(元データ)
・ラグ特徴量のデータセット作成
・PLSの実行(ラグ特徴量)
・Random Forest(RF)の回帰分析結果
・参考文献
目次
最終成果物(Pythonコード)
ソースコードはGitHubに公開しています。
回帰モデルは、線形のPLSと非線形のRandom Forest(RF)の2ケースを用意しました。
それでは、毎度のごとく脱ブタン塔のサンプルデータを使っていきます。
サンプルデータの入手
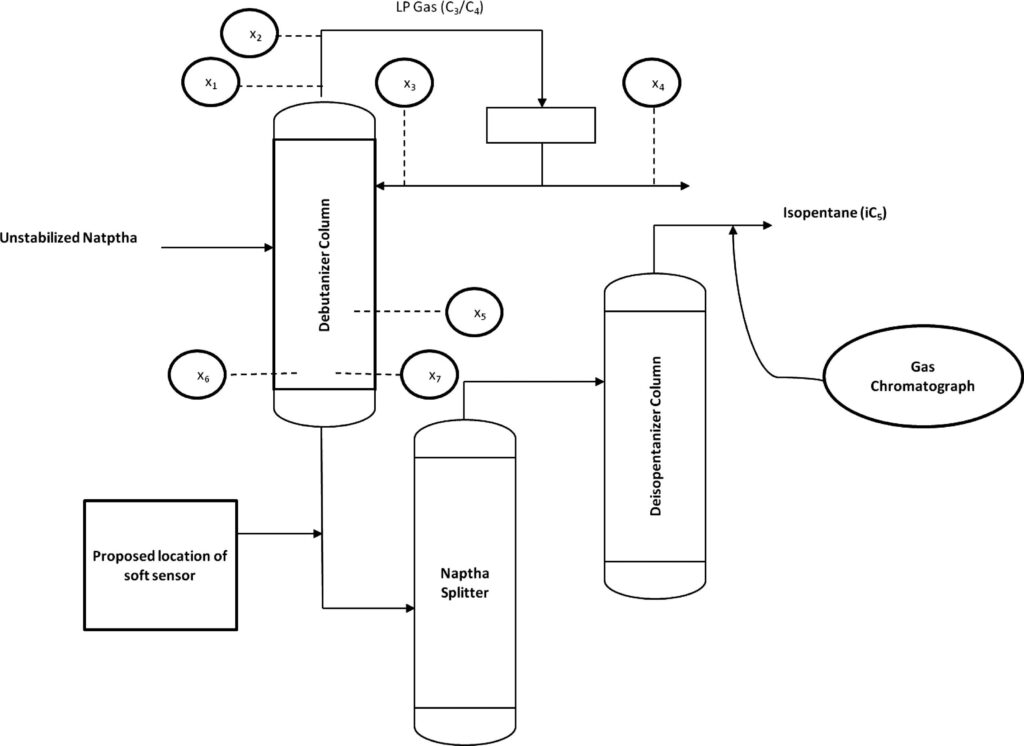
コチラのGitHubページで入手できる「debutanizer_data.csv」を利用します。
脱ブタン塔のプロセスデータであり、プロセスフローは上図の通りです。
説明変数がx1〜x7の7個で、目的変数がyの1個、サンプル数は2394個です。
| 変数名 | 詳細 | 日本語訳 |
|---|---|---|
| x1 | Top Temperature | 塔頂温度 |
| x2 | Top pressure | 塔頂圧力 |
| x3 | Reflux flow | 還流流量 |
| x4 | Flow to next process | 次プロセスへの流量 |
| x5 | 6th tray Temperature | 6段目温度 |
| x6 | Bottom Temperature1 | 塔底温度1 |
| x7 | Bottom Temperature2 | 塔底温度2 |
| y | Butane(C4) content in the debutanizer column bottom | 塔底におけるブタン含有量 |
データの読み込み
「debutanizer_data.csv」と同じフォルダに、「lag_pls_regression.ipynb」というファイルを作成しましょう。
下記のコードでライブラリのインポートとデータの読み込みを行います。
別記事で作成したコードを再利用するため、自作モジュール(regression_tools)をインポートしています。
- load_data
- evaluate_performance_std(PLS)
(evaluate_performance(RF)) - evaluate_model_std(PLS)
(evaluate_model(RF)) - perform_pls_regression(PLS)
(perform_rf_regression(RF))
自作モジュール(regression_tools)の中身についてはコチラを参照してください。
import pandas as pd import numpy as np #自作モジュール from regression_tools import load_data, evaluate_performance_std, evaluate_model_std, perform_pls_regression df = load_data()
PLSの実行(元データ)
得られたデータセットを説明変数Xと目的変数yに分割し、PLSを実行しましょう!
# 説明変数Xと目的変数yに分割 X = df.iloc[:, :-1] y = df.iloc[:, -1] # 関数の実行 best_components, standard_regression_coefficients, beta_train, intercept_train = perform_pls_regression(X, y)
perform_pls_regression関数の中身については、下記の記事で解説しています。
-

-
【Python】部分的最小二乗回帰(PLS)を使ってみよう!
続きを見る
それでは回帰分析の結果を見てみましょう(一部抜粋)。
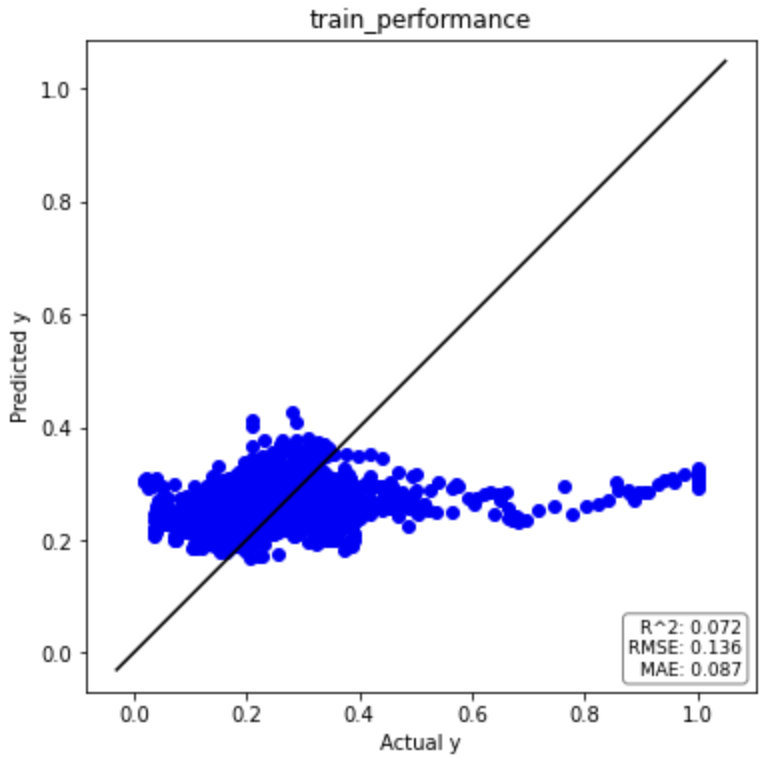
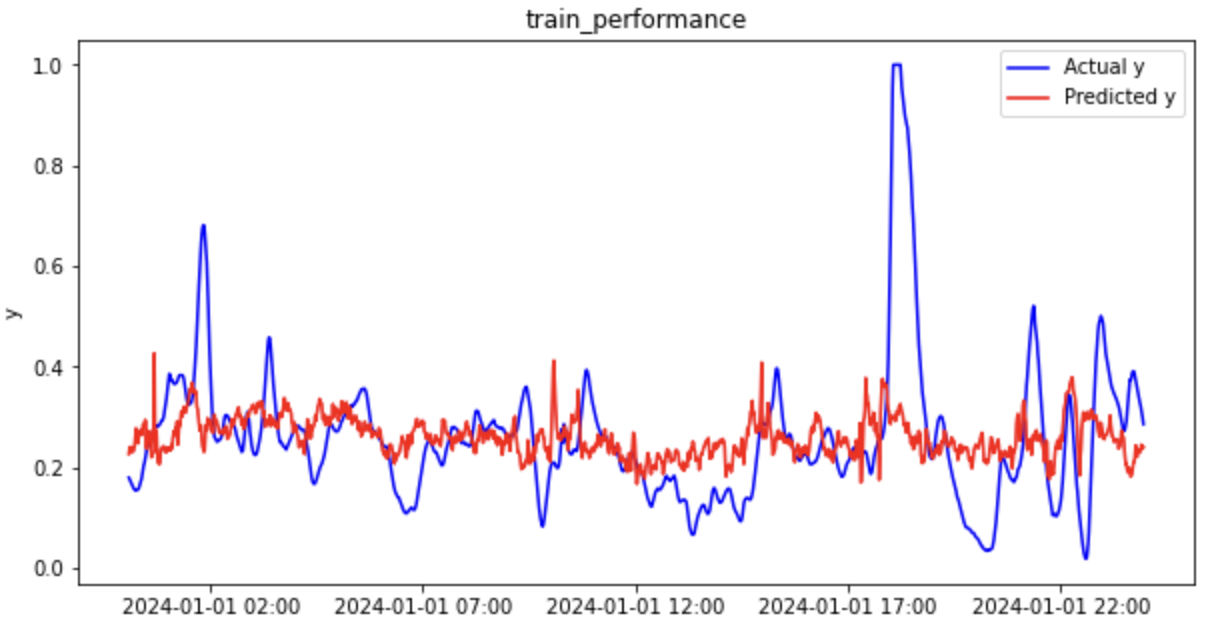
トレーニングデータ
テストデータ
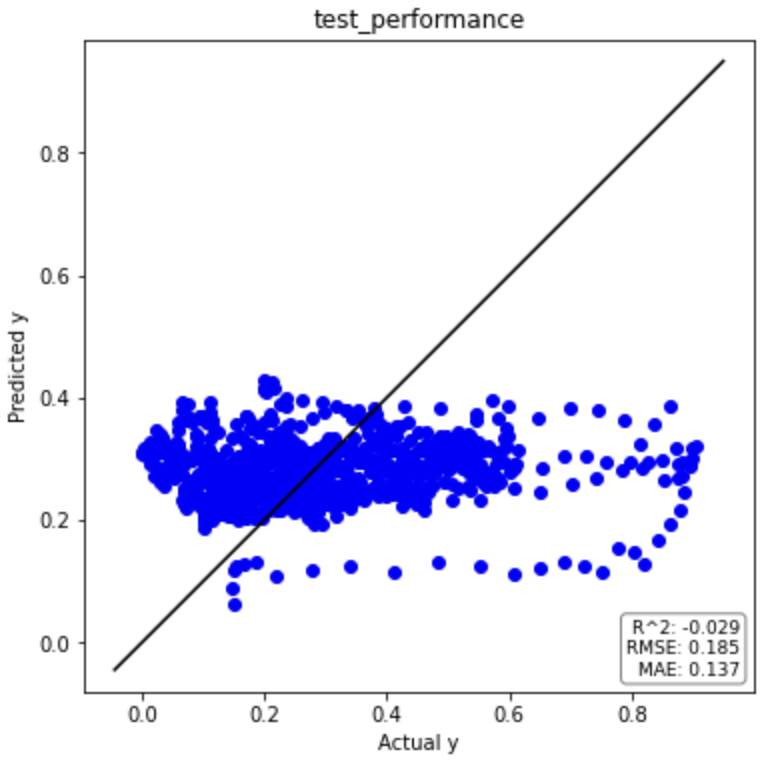
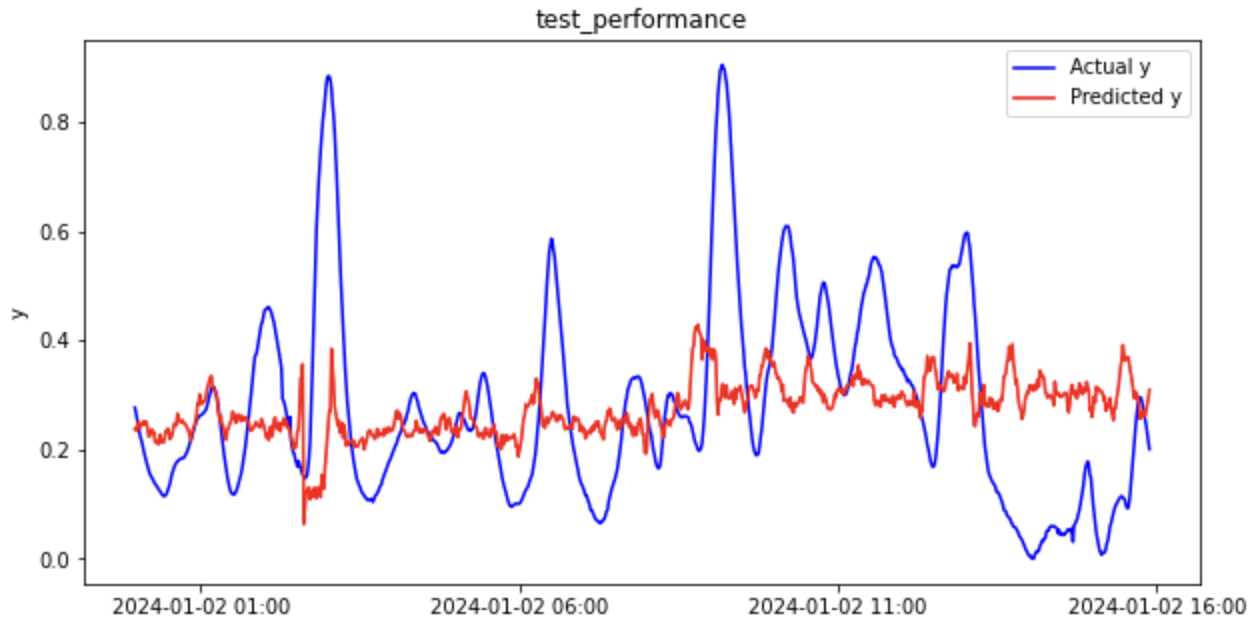
回帰分析結果まとめ(元データ)
元データの回帰分析結果を下表にまとめました。
テストデータの決定係数(R2)がマイナスになっているため、平均値で回帰するよりもパフォーマンスが悪いという結果です。
全然予測できていないですね。。
| PLS(元データ) | R2 | RMSE | MAE |
| トレーニングデータ | 0.072 | 0.136 | 0.087 |
| テストデータ | -0.029 | 0.185 | 0.137 |
ラグ特徴量のデータセット作成
下記の流れでラグ特徴量のデータセットを作成していきます。
- 各変数に対して0〜30分のラグ特徴量を作成
- それぞれのラグ特徴量と目的変数yとの相関係数を計算
- 各変数について相関係数の絶対値が最大のラグを抽出
- 最も相関の強いラグ特徴量のみを含むデータフレームを作成
pythonコードは下記の通りです。
# データフレームを用意
correlations = pd.DataFrame()
# ラグ0から30までの特徴量を作成し、yとの相関を計算
for col in X.columns: # yを除く全てのカラムに対して
for lag in range(31): # ラグ0から30まで
X_lagged = X[col].shift(lag)
corr = X_lagged.corr(y)
correlations.loc[lag, col] = corr
# 各カラムに対して相関係数の絶対値が最大のラグを抽出
best_lags = correlations.abs().idxmax()
# 最も相関が強いラグ特徴量だけを含むデータセットを作成
df_lag = pd.DataFrame()
for col, lag in best_lags.items():
df_lag[f'{col}_lag_{lag}'] = X[col].shift(lag)
# NaN値を削除
df_lag['y'] = y
df_lag.dropna(inplace=True)
# 結果を表示
df_lag
上記コードを実行すると、下図のようなラグ特徴量のデータセットが作成できました。
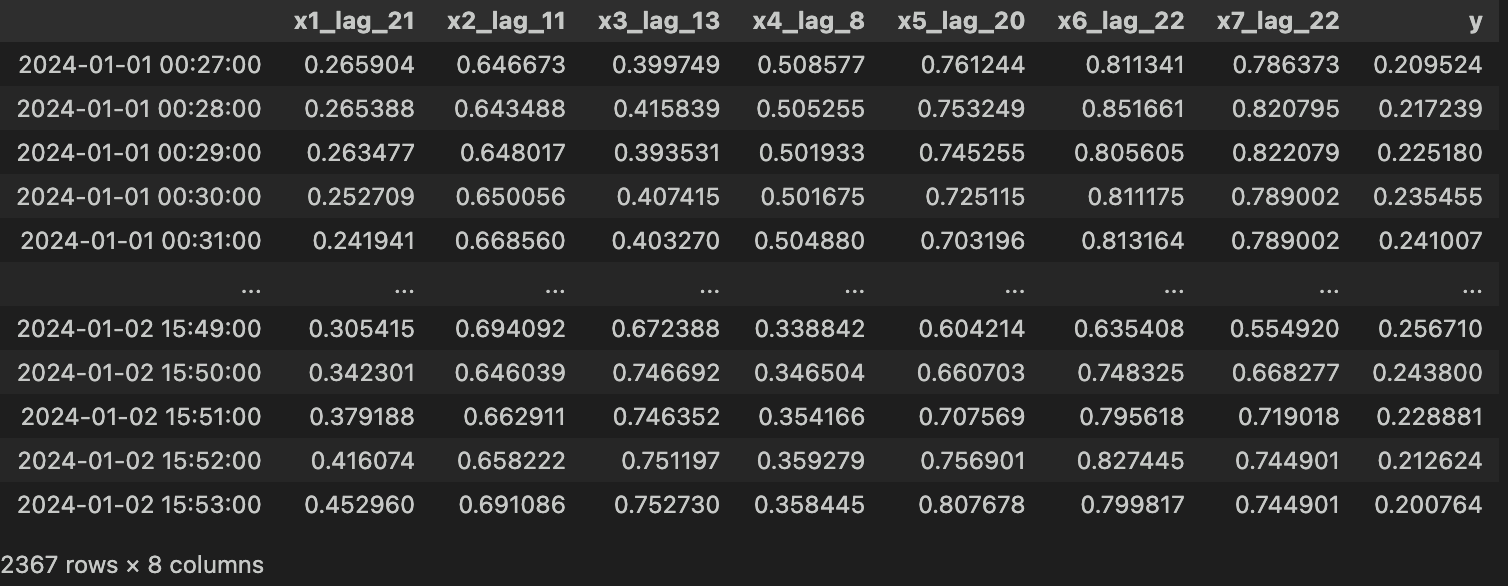
目視確認 Ver.
ちなみに、結果にいまいち自信がもてない場合は、目視で確認しながら実行する方法があります。
下記の記事でラグ特徴量(時間遅れ変数)の相関係数をチェックする可視化ツールを作成しています。
Streamlitライブラリを用いて、簡単に可視化ツールを作成することができます。
-

-
【Python】ラグ特徴量(時間遅れ変数)の相関係数
続きを見る
また、Stremlit Shareで可視化ツールを公開しているので、一旦コチラを見てください。
最も相関係数の絶対値が大きくなるラグ特徴量(時間遅れ変数)を探索してみると下表の通りです。
| 説明変数 | ラグ(時間遅れ) [分] |
| x1 | 21 |
| x2 | 11 |
| x3 | 13 |
| x4 | 8 |
| x5 | 20 |
| x6 | 22 |
| x7 | 22 |
この数値を使ってラグ特徴量のデータセットを作成するpythonコードは下記の通りです。
先ほど作成したものと全く同じラグ特徴量のデータセットが得られます。
# ラグの値(目視確認)
lags = [21, 11, 13, 8, 20, 22, 22]
# 新しいデータフレームを作成
df_lag = pd.DataFrame(index=X.index)
# 各変数に対して指定されたラグを適用
for i, lag in enumerate(lags, start=1):
df_lag[f'x{i}_lag_{lag}'] = X[f'x{i}'].shift(lag)
# 目的変数 y もデータフレームに追加
df_lag['y'] = y
# NaN値を含む行を削除
df_lag.dropna(inplace=True)
# 結果を表示
df_lag
PLSの実行(ラグ特徴量)
得られたラグ特徴量のデータセット(df_lag)を説明変数Xと目的変数yに分割し、PLSを実行しましょう!
# 説明変数Xと目的変数yに分割 X_lag = df_lag.iloc[:, :-1] y_lag = df_lag.iloc[:, -1] # 関数の実行 best_components, standard_regression_coefficients, beta_train, intercept_train = perform_pls_regression(X_lag, y_lag)
それでは、元データと同様に回帰分析の結果を見てみましょう(一部抜粋)。
トレーニングデータ
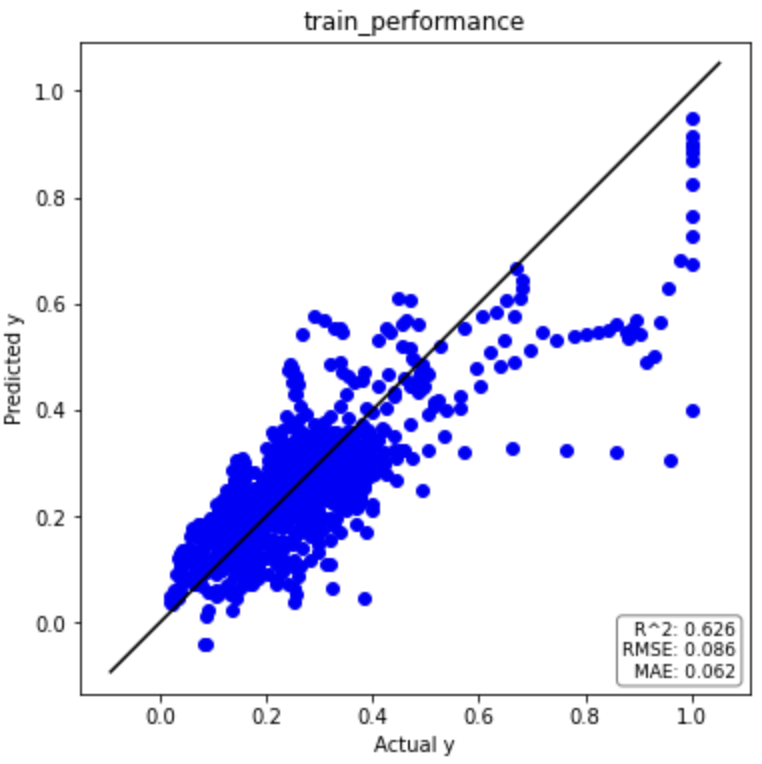
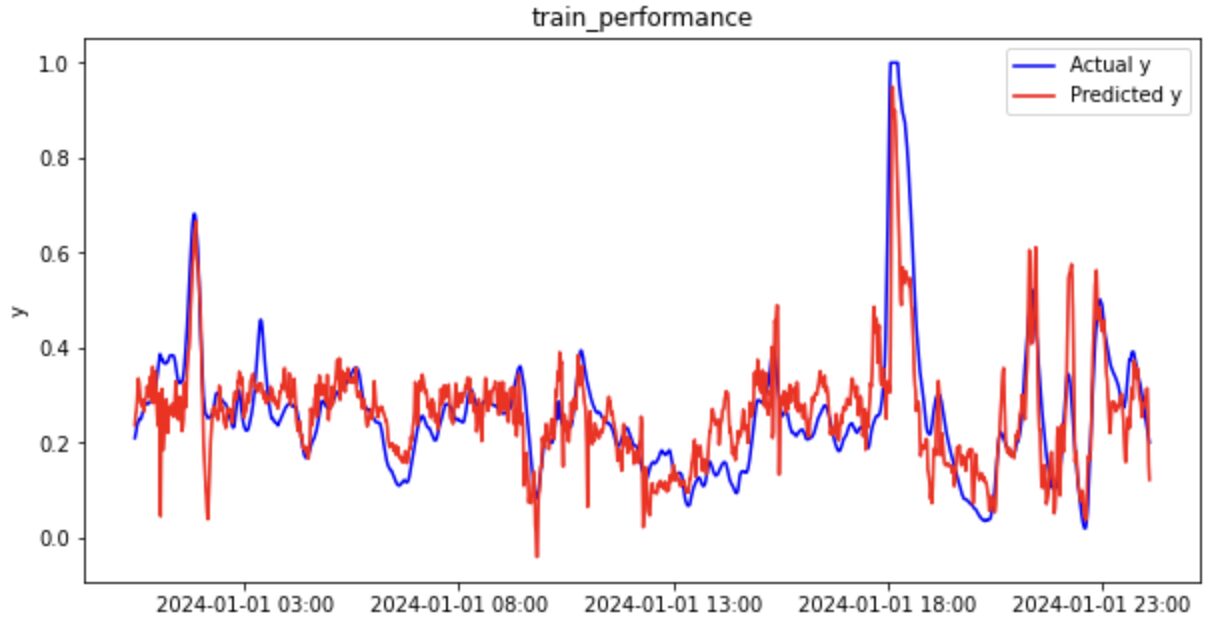
テストデータ
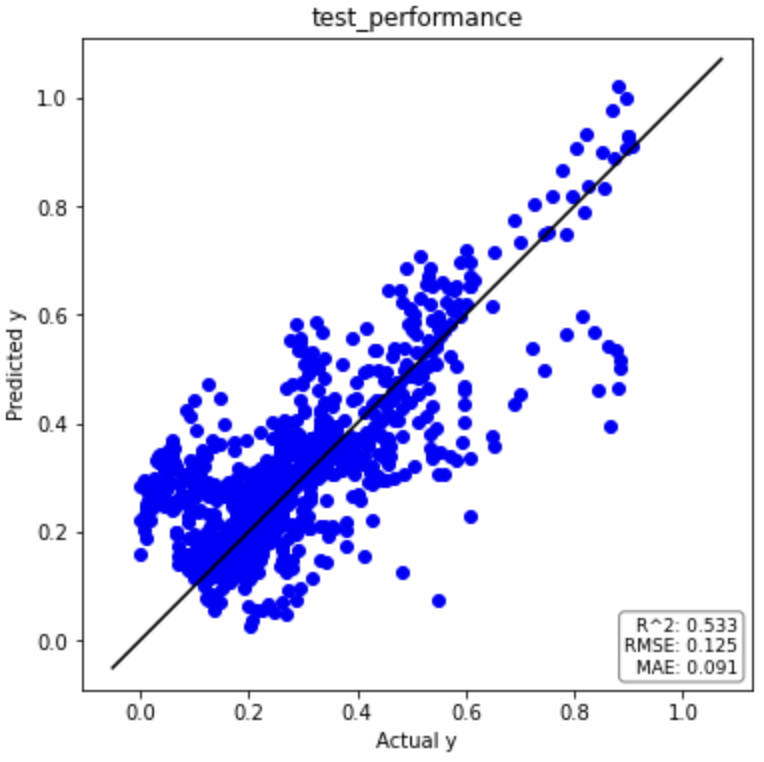
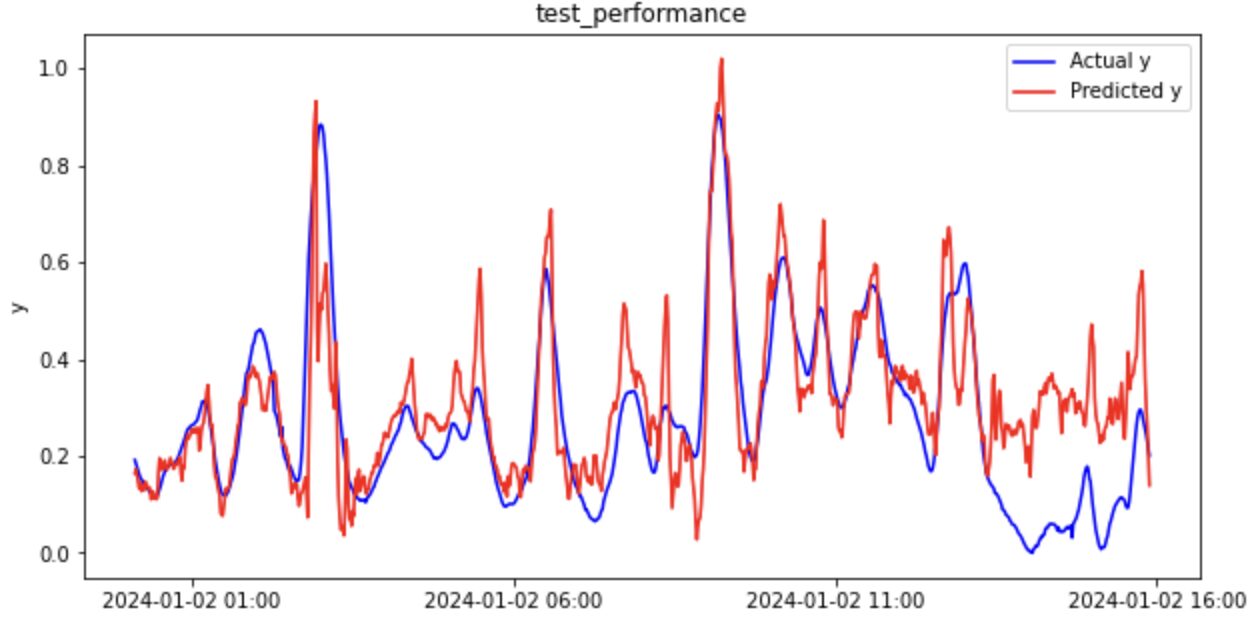
回帰分析結果のまとめ(ラグ特徴量)
元データとラグ特徴量のデータセットによる回帰分析結果を下表にまとめました。
ラグ特徴量(時間遅れ変数)を考慮することで予測精度が劇的に改善していることがわかります。
| PLS(元データ) | R2 | RMSE | MAE |
| トレーニングデータ | 0.072 | 0.136 | 0.087 |
| テストデータ | -0.029 | 0.185 | 0.137 |
| PLS(ラグ特徴量) | R2 | RMSE | MAE |
| トレーニングデータ | 0.626 | 0.086 | 0.062 |
| テストデータ | 0.533 | 0.125 | 0.091 |
Random Forest(RF)の回帰分析結果
詳細は割愛しますが、Random Forest(RF)でも同様のことをやってみましょう。
pythonコードはコチラ(GitHub)に記載しています。
それでは、回帰分析結果のみ下表に示します。
| RF(元データ) | R2 | RMSE | MAE |
| トレーニングデータ | 0.438 | 0.106 | 0.072 |
| テストデータ | -0.048 | 0.186 | 0.145 |
| RF(ラグ特徴量) | R2 | RMSE | MAE |
| トレーニングデータ | 0.708 | 0.076 | 0.054 |
| テストデータ | 0.552 | 0.122 | 0.090 |
PLSと同様、Random Forestでもラグ特徴量を考慮することで予測精度が劇的に改善していることがわかります。
参考文献
ラグ特徴量(時間遅れ変数)について簡単に解説してくれています。
部分的最小二乗回帰(PLS)や回帰分析結果のまとめ方はこちらの書籍を参考にしました。
ランダムフォレスト回帰については、こちらの書籍を参考にしました。