どうも。こんにちは。
ケミカルエンジニアのこーしです。
本日は、「決定木とランダムフォレストによる重回帰分析」についてわかりやすく解説します。
実務では、説明変数\(X\)と目的変数\(y\)との間に、非線形の関係性があることが多々あります。
線形回帰モデルでも、説明変数\(X\)の「二乗項」や「交差項」を特徴量に追加することで、非線形性を考慮することができます。
しかし、実際には二乗ではなく、三乗、四乗、0.5乗が良いかも知れませんし、指数関数や対数関数に変換する必要があるかも知れません。
そこで、本記事では上記のように特徴量を追加することなく非線形性を考慮できる回帰分析手法として、決定木とランダムフォレストを紹介します。
本記事を読めば、非線形の重回帰分析が簡単にできるようになります!
本記事の内容
・決定木(DT)とは
・ランダムフォレスト(RF)とは
・サンプルデータの入手
・【Python】DTとRFの重回帰分析
・回帰分析結果
・参考文献
目次
決定木(DT)とは
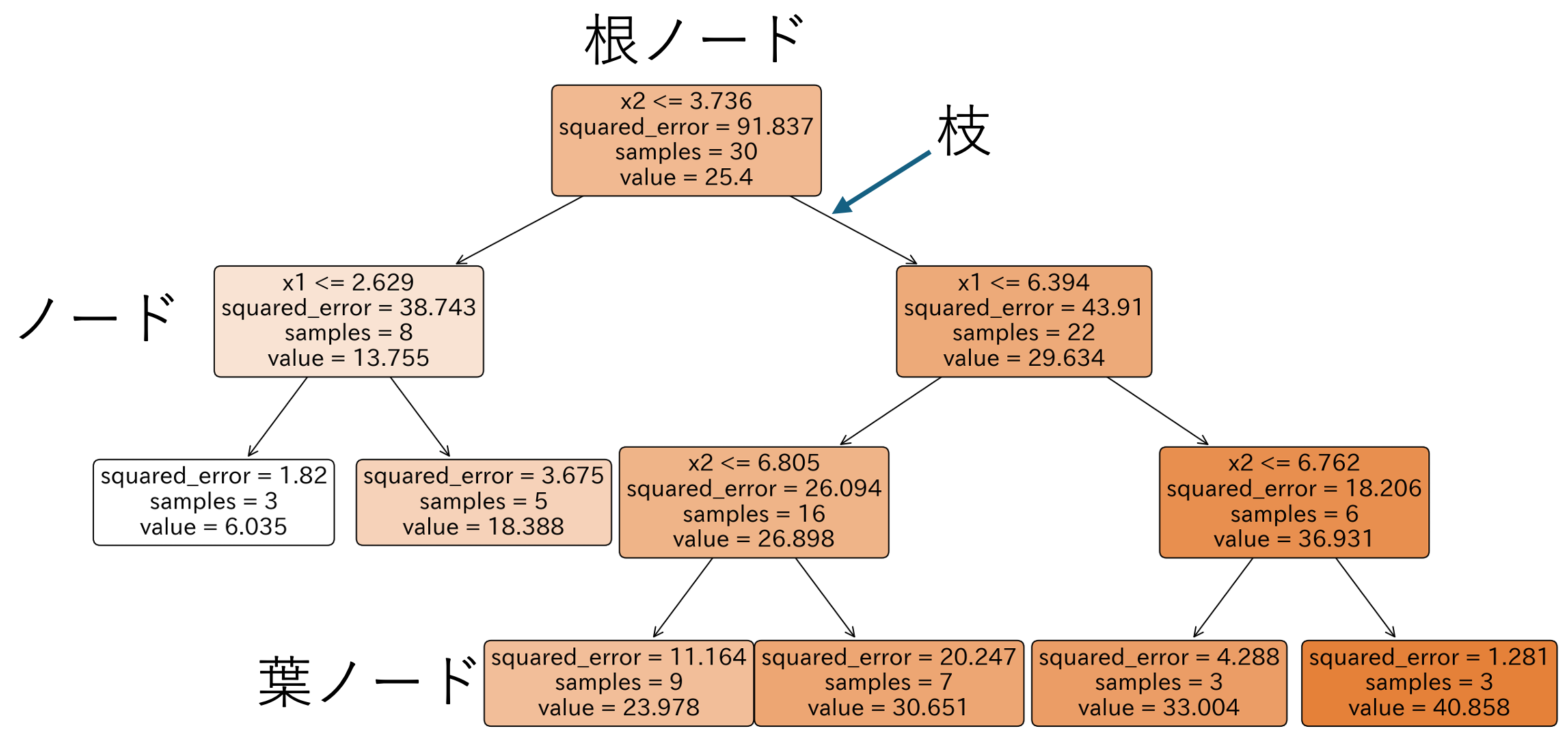
上図のように、説明変数\(X\)を各領域内の目的変数 \(y\)が類似するように分割します。
分割されたサンプルの集まりを「ノード」と呼び、最初に分割を行うノードを「根ノード」、末端のノードを「葉ノード」と呼びます。
上図のように、分割されたノードが「木構造」となるため「決定木(Decision Tree:DT)」と呼ばれています。
また、決定木で分割された説明変数\(X\)は下図のようなイメージとなります。
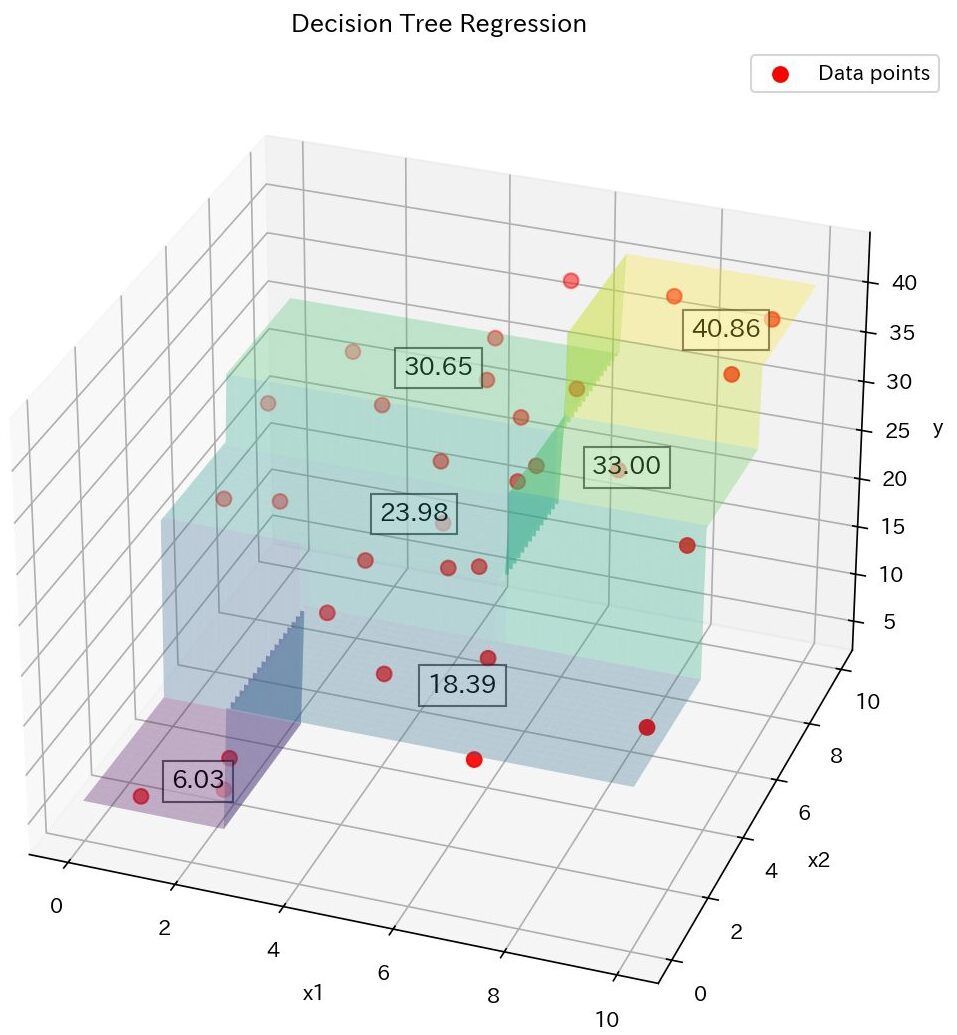
似たような \(y\)が集まったノードに分割されていることがわかりますね。
どのように分割していくのかというと、分割後の2つのノードにおける評価関数\((E_1,E_2)\)の和\((E = E_1 + E_2)\)が最小となるような閾値を探索します。
評価関数\(E_i\)(\(i = 1,2\))は、分割後のそれぞれのノードにおける目的変数\(y\)の「誤差の2乗和」です。
$$E_i = \sum (y - \bar{y})^2\tag{1}$$
よって、各ノードの評価関数\(E_i\)の和を最小にすることで、類似した目的変数\(y\)の集まりでノードを分割できるということです。
ハイパーパラメータ
事前に設定すべきパラメータを「ハイパーパラメータ」と呼び、決定木では下記2つのハイパーパラメータがあります。
決定木のハイパーパラメータ
- 葉ノードにおけるサンプル数の下限
- 木の深さの上限
決定木の欠点
決定木は、モデルが解釈しやすい反面、説明変数\(X\)と目的変数\(y\)の関係が複雑な場合は、推定精度が悪くなる傾向があります。
また、決定木モデルにおける目的変数\(y\)の推定値は、分割したサンプル群の"平均値"で表されるため、既存データの最大・最小値の範囲内に限定されてしまいます。
ランダムフォレスト(RF)とは
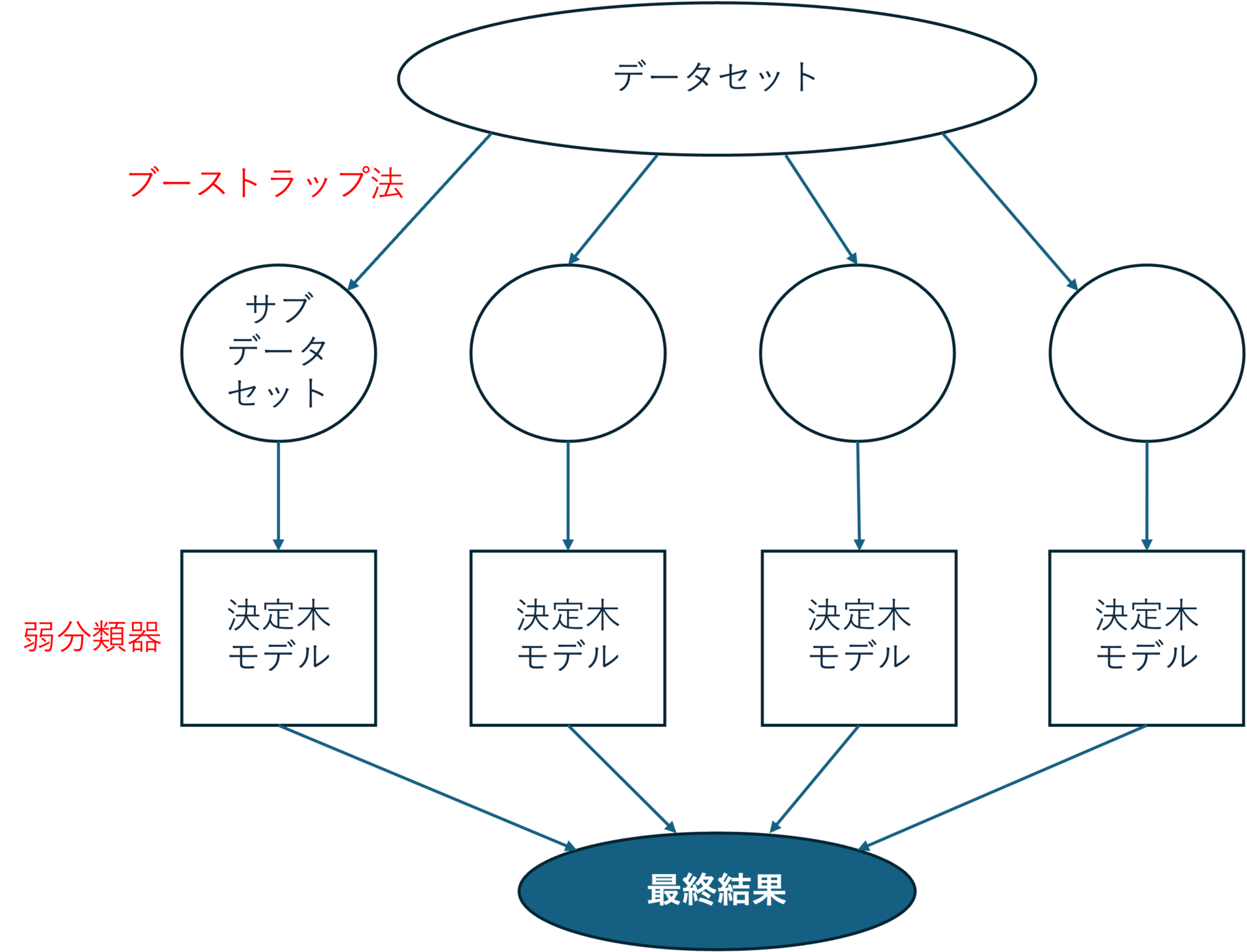
ランダムフォレスト(Random Forest:RF)は、上図のようにたくさんの「決定木モデル」を組み合わせて、より正確な予測を行う方法です。
新しいサンプルにおける目的変数\(y\)の推定値は、すべての決定木モデルにおける推定値の平均値を出力します。
例えると、たくさんの専門家の意見を聞き、すべての専門家の意見を総合した結果を最終結果とすることに似ています。
アンサンブル学習法
ランダムフォレストを専門用語を使って説明すると下記の通りです。
ランダムフォレストとは
決定木をバギングの弱分類器として採用したアンサンブル学習アルゴリズム
アンサンブル学習とは、複数の学習器(モデル)を組み合わせて、より精度の高いモデルを構築する手法です。
アンサンブル学習の代表的な手法には、バギングやブースティングなどがあります。
バギング
ランダムフォレストでは、バギングという手法が用いられています。
バギングとは、ブーストラップ法でデータセットからランダムに一部のサンプルを取り出し、これを繰り返して多数のサブデータセットを作り出して、それぞれで学習器(モデル)を作成し多数決を取る手法です。
ブーストラップ法
ブーストラップ法とは、1つのデータセットから復元抽出を繰り返して多数のサブデータセットを作成するサンプリング手法です。
復元抽出は、重複を許してランダムにサンプリングするため、サブデータセット毎に選択されてないサンプルが存在します。
これをOut-Of-Bag(OOB)と呼び、クロスバリデーションの代わりにOOBの推定値に基づいてハイパーパラメータを選択することができます。
サンプルデータの入手
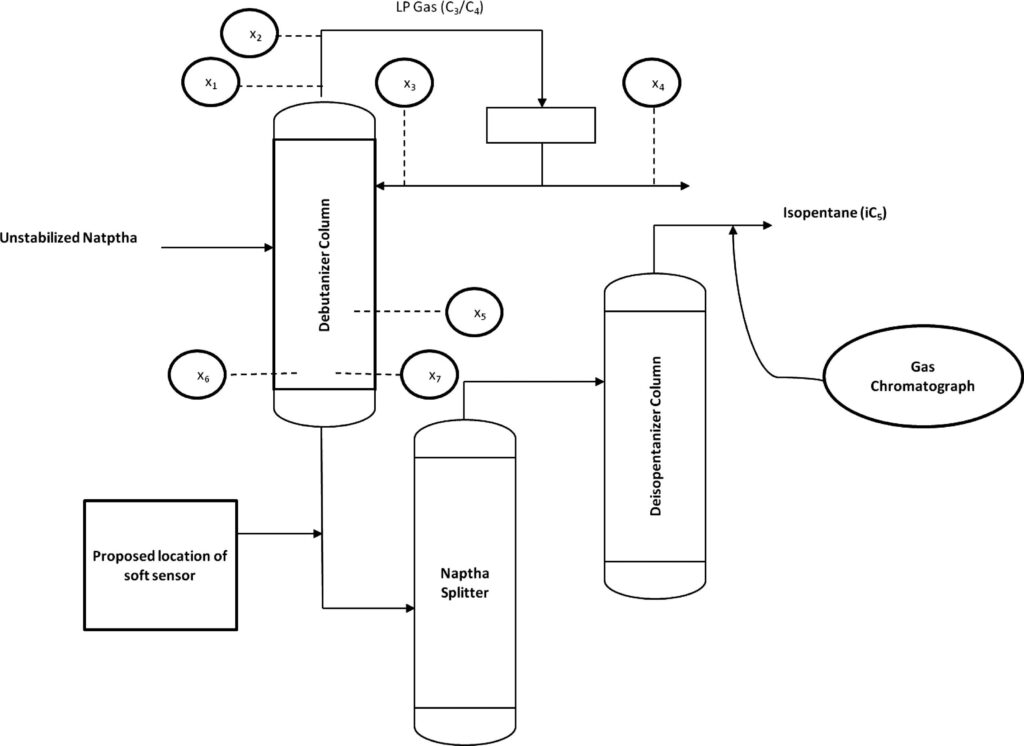
コチラのGitHubページで入手できる「debutanizer_data.csv」を利用します。
脱ブタン塔のプロセスデータであり、プロセスフローは上図の通りです。
説明変数がx1〜x7の7個で、目的変数がyの1個、サンプル数は2394個です。
| 変数名 | 詳細 | 日本語訳 |
|---|---|---|
| x1 | Top Temperature | 塔頂温度 |
| x2 | Top pressure | 塔頂圧力 |
| x3 | Reflux flow | 還流流量 |
| x4 | Flow to next process | 次プロセスへの流量 |
| x5 | 6th tray Temperature | 6段目温度 |
| x6 | Bottom Temperature1 | 塔底温度1 |
| x7 | Bottom Temperature2 | 塔底温度2 |
| y | Butane(C4) content in the debutanizer column bottom | 塔底におけるブタン含有量 |
データの読み込み
「debutanizer_data.csv」と同じフォルダに、「dt_rf_regression.ipynb」(dt_rf_regression.pyでも可)というファイルを作成しましょう。
下記のコードでライブラリのインポートと、データの読み込みを行います。
ここでは、下記3つのデータの前処理を行っています。
- 時系列データなので、実務データを想定しインデックスに時刻を割り振る
- 目的変数yの測定時間を考慮し、5分(行)だけデータをずらす
- プロセス知見より、目的変数yと説明変数x1〜x7の時間差を18分とする(時間遅れ変数の作成)
import math import pandas as pd import numpy as np import matplotlib.pyplot as plt import matplotlib.dates as mdates from sklearn import metrics from sklearn.model_selection import train_test_split, KFold, cross_val_predict from sklearn.tree import DecisionTreeRegressor, plot_tree from sklearn.ensemble import RandomForestRegressor
#脱ブタン塔のプロセスデータを読み込む
df = pd.read_csv('debutanizer_data.csv')
#時系列データなので、実務データを想定しindexに時刻を割り当てる
# 開始日時を指定
start_datetime = '2024-01-01 00:00:00'
# DataFrameの長さを取得
n = len(df)
# 日時インデックスを生成(1分間隔)
date_index = pd.date_range(start=start_datetime, periods=n, freq='T')
# DataFrameのインデックスを新しい日時インデックスに設定
df.index = date_index
# 目的変数の測定時間を考慮(5分間)
df['y'] = df['y'].shift(5)
#yがnanとなる期間のデータを削除
df = df.dropna()
#説明変数と目的変数にわける
X = df.iloc[:, :-1]
y = df['y']
#時間遅れ変数を作成
delay_number = 18
X_with_delays = pd.DataFrame()
for col in X.columns:
col_name = f"{col}_delay_{delay_number}"
X_with_delays[col_name] = X[col].shift(delay_number)
# 時間遅れ変数とyのデータフレームを作成
X_with_delays['y'] = y
X_with_delays = X_with_delays.dropna()
# 目的変数と説明変数に分割
X = X_with_delays.iloc[:, :-1]
y = X_with_delays['y']
【Python】DTとRFの重回帰分析
サンプルデータを読み込んだら、決定木(DT)とランダムフォレスト(RF)の回帰モデルを作成していきましょう。
下記の書籍を参考にして、ChatGPTに聞きながらpythonコードを作成しました。
まず、下記4つのモジュールを作成します。
- evaluate_performance
- evaluate_model
- perform_dt_regression
- perform_rf_regression
def evaluate_performance(X, y, model, save_to_csv=False, filename='performance.csv'):
"""
モデルの性能を評価し、結果をプロットします。
オプションで予測結果をCSVファイルに保存します。
Parameters:
X : pd.DataFrame
説明変数のデータセット
y : pd.Series
目的変数の値
model : sklearn model
評価する訓練済みのモデル
save_to_csv : bool, optional
結果をCSVファイルに保存するかどうかを指定 (default is False)
filename : str, optional
出力するCSVファイルの名前 (default is 'performance.csv')
Returns:
r2 : 決定係数R^2
rmse : RMSE
mae : MAE
"""
# yの推定値を算出
y_pred = model.predict(X)
# 性能指標の算出
r2 = metrics.r2_score(y, y_pred)
rmse = np.sqrt(metrics.mean_squared_error(y, y_pred))
mae = metrics.mean_absolute_error(y, y_pred)
print(f"R^2: {r2:.3f}, RMSE: {rmse:.3f}, MAE: {mae:.3f}")
# プロットの作成
plt.figure(figsize=(6, 6))
plt.scatter(y, y_pred, color='blue')
y_max = max(y.max(), y_pred.max())
y_min = min(y.min(), y_pred.min())
# 取得した最小値-5%から最大値+5%まで、対角線を作成
plt.plot([y_min - 0.05 * (y_max - y_min), y_max + 0.05 * (y_max - y_min)],
[y_min - 0.05 * (y_max - y_min), y_max + 0.05 * (y_max - y_min)], 'k-')
plt.ylim(y_min - 0.05 * (y_max - y_min), y_max + 0.05 * (y_max - y_min))
plt.xlim(y_min - 0.05 * (y_max - y_min), y_max + 0.05 * (y_max - y_min))
plt.xlabel('Actual y')
plt.ylabel('Predicted y')
# テキストボックスを右下に配置
plt.text(0.98, 0.02, f'R^2: {r2:.3f}\nRMSE: {rmse:.3f}\nMAE: {mae:.3f}', transform=plt.gca().transAxes,
fontsize=9, verticalalignment='bottom', horizontalalignment='right',
bbox=dict(boxstyle="round,pad=0.3", edgecolor='black', facecolor='white', alpha=0.5))
plt.title(filename[:-4])
plt.grid(False)
plt.axis('equal')
plt.show()
# 時系列のプロット
plt.figure(figsize=(10, 5))
plt.gca().xaxis.set_major_formatter(mdates.DateFormatter('%Y-%m-%d %H:%M')) # 日時形式を設定
plt.gca().xaxis.set_major_locator(mdates.HourLocator(interval=5)) # 5時間ごとに目盛りを設定
plt.plot(y.index, y, label='Actual y', color='blue', marker='', linestyle='-')
plt.plot(y.index, y_pred, label='Predicted y', color='red', marker='', linestyle='-')
#plt.gcf().autofmt_xdate() # x軸のラベルを自動で斜めにして読みやすくする
plt.ylabel('y')
plt.title(filename[:-4])
plt.legend()
plt.show()
# データの保存
if save_to_csv:
results_df = pd.DataFrame({
'Actual': y,
'Predicted': y_pred.flatten(),
'Error': y - y_pred.flatten()
})
results_df.to_csv(filename, index=False)
print(f"Data saved to {filename}")
return r2, rmse, mae
def evaluate_model(X_train, y_train, X_test, y_test, model, save_csv=False, train_filename='train_performance.csv', test_filename='test_performance.csv'):
"""
トレーニングデータとテストデータの両方でモデルの性能を評価します。
Parameters:
X_train : pd.DataFrame
トレーニングデータの説明変数
y_train : pd.Series
トレーニングデータの目的変数
X_test : pd.DataFrame
テストデータの説明変数
y_test : pd.Series
テストデータの目的変数
model : sklearn model
評価する訓練済みのモデル
save_csv : bool, optional
結果をCSVファイルに保存するかどうかを指定 (default is False)
train_filename : str, optional
トレーニングデータの予測結果を保存するCSVファイルの名前 (default is 'train_performance.csv')
test_filename : str, optional
テストデータの予測結果を保存するCSVファイルの名前 (default is 'test_performance.csv')
"""
print("Evaluating Training Data")
evaluate_performance(X_train, y_train, model, save_to_csv=save_csv, filename=train_filename)
print("Evaluating Test Data")
evaluate_performance(X_test, y_test, model, save_to_csv=save_csv, filename=test_filename)
def perform_dt_regression(X, y, fold_number=5, test_size=0.4, min_samples_leaf=3, shuffle=False):
"""
決定木(DT)モデルを構築し、クロスバリデーションを用いて木の深さを最適化します。
その後、最適な木の深さでモデルを再構築し、トレーニングデータとテストデータの性能を評価します。
Parameters:
X : pd.DataFrame
説明変数のデータセット
y : pd.Series
目的変数のデータ
fold_number : int, optional
クロスバリデーションで使用するフォールドの数 (default is 5)。
test_size : float, optional
データを分割する際のテストデータの割合 (default is 0.4)。
min_samplts_leaf : int, optional
葉ノードごとのサンプル数の最小値 (default is 3)。
shuffle : bool, optional
データ分割時にデータをシャッフルするかどうか (時系列データを想定し、デフォルトはFalse)。
Returns:
optimal_max_depth : 最適な木の深さ
dt_final : 最終的な決定木モデル
"""
# データの分割
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=test_size, shuffle=shuffle, random_state=0)
# 木の深さを決定するためのクロスバリデーション
cross_validation = KFold(n_splits=fold_number, shuffle=False)
max_depths = np.arange(1, 31)
r2_scores = []
for max_depth in max_depths:
dt = DecisionTreeRegressor(max_depth=max_depth, min_samples_leaf=min_samples_leaf, random_state=0)
y_cv = cross_val_predict(dt, X_train, y_train, cv=cross_validation)
r2 = metrics.r2_score(y_train, y_cv)
r2_scores.append((max_depth, r2))
# r2_scoresをグラフで表示
number_of_max_depth = [item[0] for item in r2_scores]
r2_values = [item[1] for item in r2_scores]
plt.figure(figsize=(8, 5))
plt.plot(number_of_max_depth , r2_values, marker='o', linestyle='-', color='b')
plt.xlabel('Number of max_depth')
plt.ylabel('R2 Score (CV)')
plt.grid(True)
plt.show()
# 最適な木の深さの決定
optimal_max_depth = max(r2_scores, key=lambda item: item[1])[0]
print(f"Optimal number of max_depth: {optimal_max_depth}")
# 最適な木の深さで決定木モデルを作成
dt_final = DecisionTreeRegressor(max_depth=optimal_max_depth, min_samples_leaf=min_samples_leaf, random_state=0)
dt_final.fit(X_train, y_train)
evaluate_model(X_train, y_train, X_test, y_test, model=dt_final)
return optimal_max_depth, dt_final
def perform_rf_regression(X, y, number_of_trees=300, test_size=0.4, shuffle=False):
"""
ランダムフォレスト(RF)モデルを構築し、OOBを用いて説明変数の数の割合を最適化します。
その後、最適な説明変数の数の割合でモデルを再構築し、トレーニングデータとテストデータの性能を評価します。
Parameters:
X : pd.DataFrame
説明変数のデータセット
y : pd.Series
目的変数のデータ
number_of_trees : int, optional
ランダムフォレストのサブデータセット(=決定木モデル)の数 (default is 300)。
test_size : float, optional
データを分割する際のテストデータの割合 (default is 0.4)。
min_samplts_leaf : int, optional
葉ノードごとのサンプル数の最小値
shuffle : bool, optional
データ分割時にデータをシャッフルするかどうか (時系列データを想定し、デフォルトはFalse)。
Returns:
optimal_x_variables_rate : 最適なXの数の割合
rf_final : 最終的な決定木モデル
"""
# データの分割
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=test_size, shuffle=shuffle, random_state=0)
# OOBを用いた説明変数の割合の最適化
x_variables_rates = np.arange(1, 11, dtype=float) / 10 # 決定木における X の数の割合
r2_oob = []
for x_variables_rate in x_variables_rates:
# ランダムフォレストモデルの作成
rf = RandomForestRegressor(n_estimators=number_of_trees,
max_features=int(math.ceil(X_train.shape[1] * x_variables_rate)),
oob_score=True)
# モデルの訓練
rf.fit(X_train, y_train)
r2 = metrics.r2_score(y_train, rf.oob_prediction_)
r2_oob.append((x_variables_rate, r2))
# r2_scoresをグラフで表示
components = [item[0] for item in r2_oob]
r2_values = [item[1] for item in r2_oob]
plt.figure(figsize=(8, 5))
plt.plot(components, r2_values, marker='o', linestyle='-', color='b')
plt.xlabel('rate of X-variables')
plt.ylabel('R2 Score (OOB)')
plt.grid(True)
plt.show()
# 最適なXの数の割合の決定
optimal_x_variables_rate = max(r2_oob, key=lambda item: item[1])[0]
print(f"Optimal rate of X-variables: {optimal_x_variables_rate}")
# 最適なXの数の割合でRFモデルを作成
rf_final = RandomForestRegressor(n_estimators=number_of_trees, max_depth=3,
max_features=int(math.ceil(X_train.shape[1] * optimal_x_variables_rate)),
oob_score=True) # RF モデルの宣言
rf_final.fit(X_train, y_train)
evaluate_model(X_train, y_train, X_test, y_test, model=rf_final)
return optimal_x_variables_rate
最後に、perform_dt_regressionとperform_rf_regressionモジュールを実行します。
# 関数の実行
#決定木回帰
optimal_max_depth, dt_final = perform_dt_regression(X, y)
# ツリーマップの作成
fig = plt.figure(figsize=(20, 10))
plot_tree(dt_final, feature_names=['x1', 'x2', 'x3', 'x4', 'x5', 'x6', 'x7'], filled=True, rounded=True)
# グラフをPNGファイルとして保存
plt.savefig('Decision Tree Structure_debutan.png', facecolor='white', dpi=500)
plt.show()
# ランダムフォレスト回帰
optimal_x_variables_rate, rf_final = perform_rf_regression(X, y)
回帰分析結果
上述のPythonコードによる回帰分析の結果を示します。
| 決定木(DT) | R2 | RMSE | MAE |
| トレーニングデータ | 0.671 | 0.081 | 0.058 |
| テストデータ | 0.439 | 0.137 | 0.103 |
| ランダムフォレスト(RF) | R2 | RMSE | MAE |
| トレーニングデータ | 0.733 | 0.073 | 0.053 |
| テストデータ | 0.562 | 0.121 | 0.090 |
複数の決定木モデルを用いたランダムフォレストの方が、予測精度が高いことがわかります。
それでは、各モデルの具体的な結果を見てみましょう。
決定木
CVによる最適な木の深さを決定
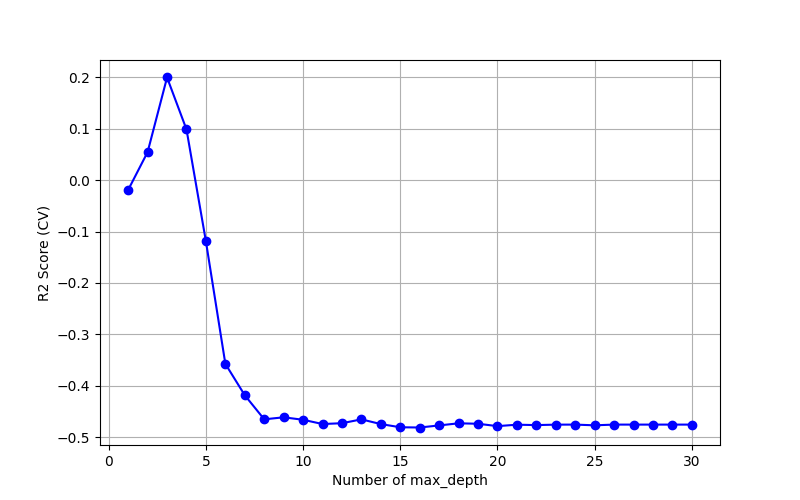
木の深さ(Number of max_depth)を変化させ、クロスバリデーションにより決定係数R2を算出し、グラフにプロットしました。
決定係数R2が最大となる最適な木の深さは3となりました。
トレーニングデータ
実測値yと予測値のプロットは下図の通りです。
プロットが対角線上に乗れば、精度良く推定できていると言えます。
また、予測精度の評価指標である決定係数R2とRMSE、MAEをグラフ中に記載しています。
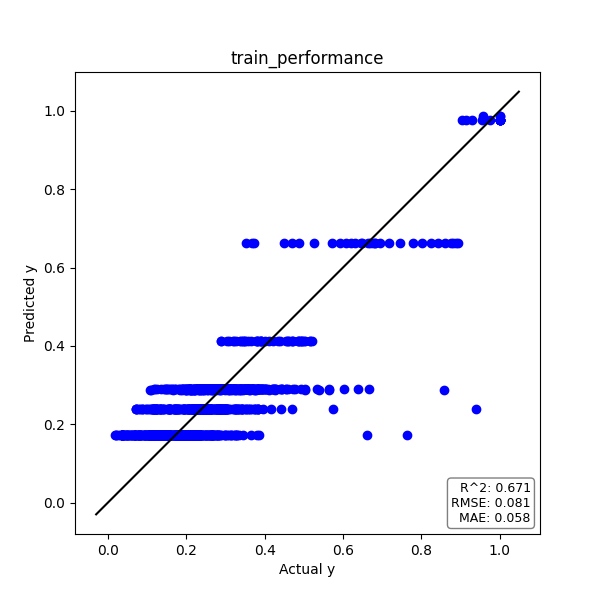
また、時系列プロットも下図に示しました。
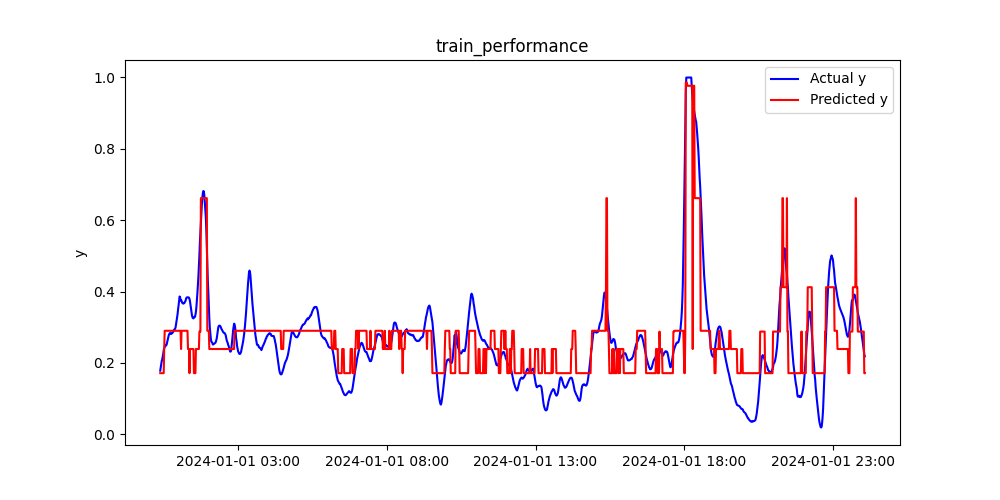
テストデータ
トレーニングデータと同様に、テストデータについても見てみましょう。
実測値yと予測値のプロット、そして時系列プロットは下図の通りです。
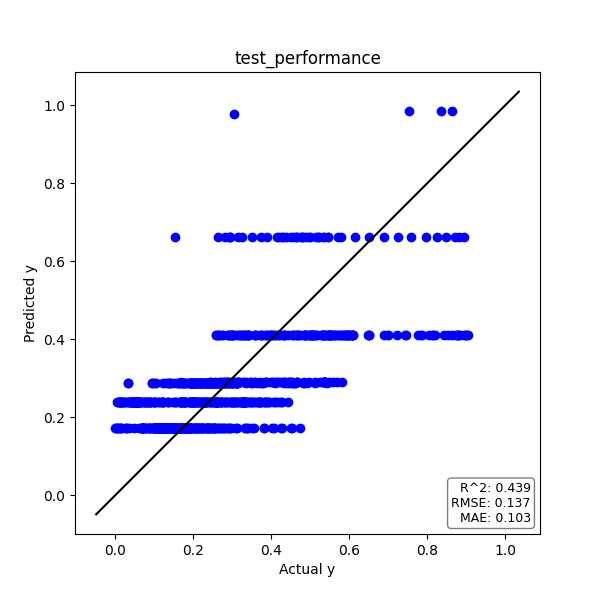
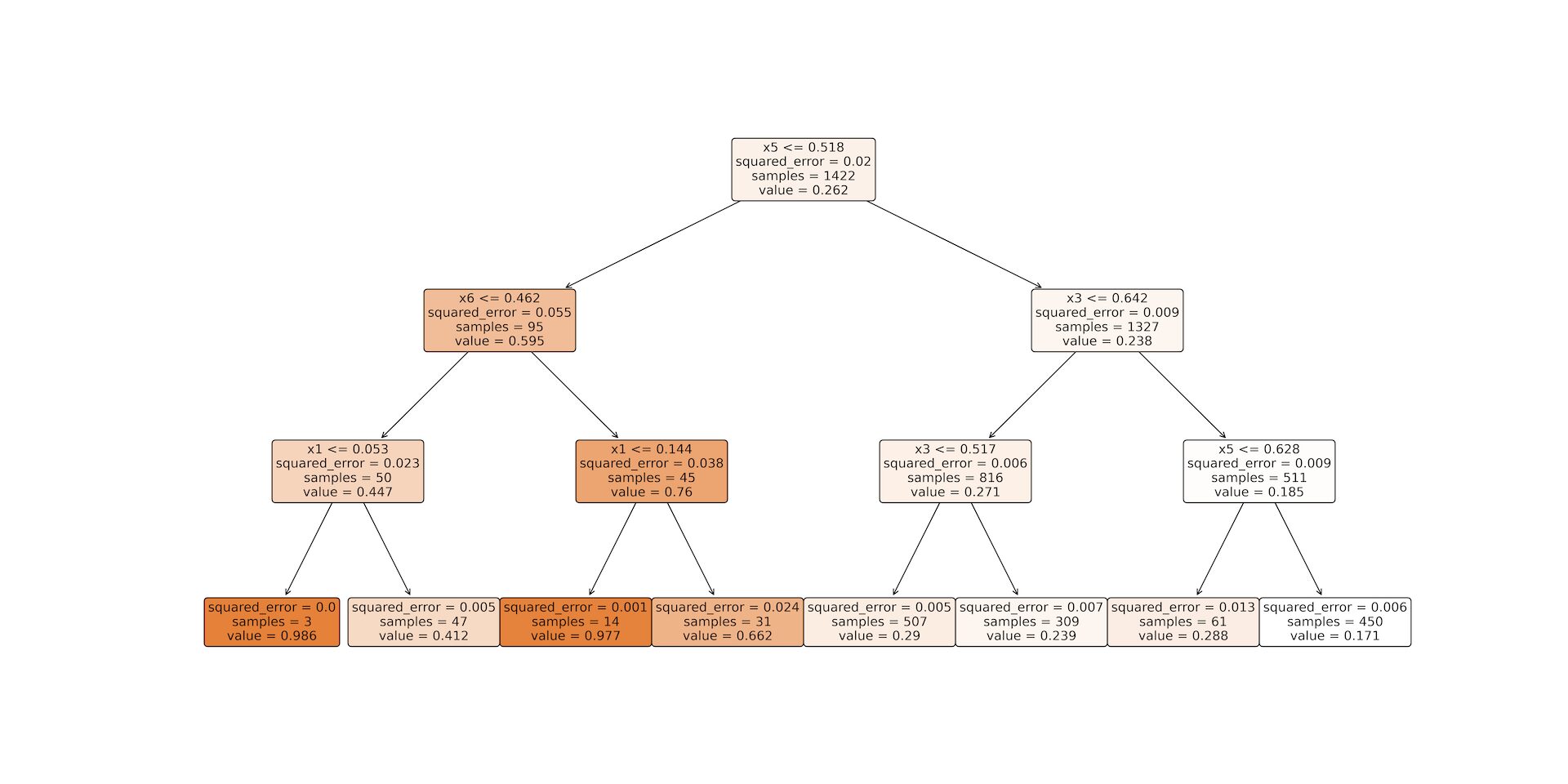
ツリーマップ
上記の決定木モデルの詳細をツリーマップにしました。
設定通り、木の深さが3になっていることがわかりますね。
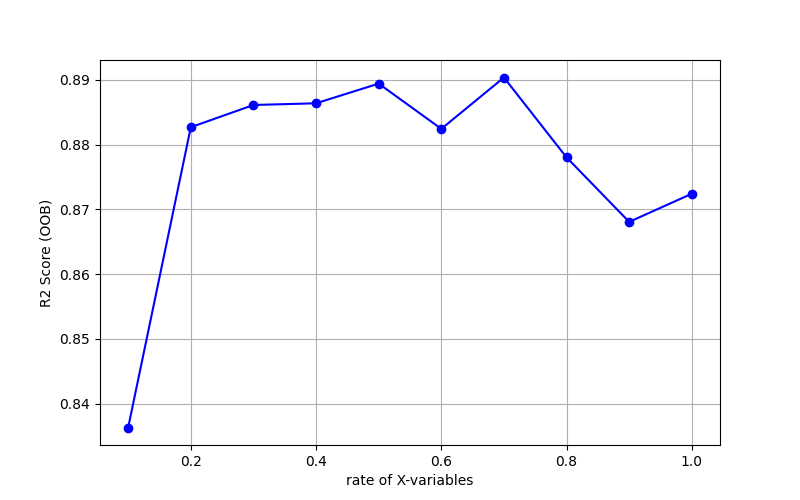
ランダムフォレスト
OOBによる説明変数の数の割合を決定
説明変数の数の割合(rate of X_variables)を変化させて、OOBにおける決定係数R2を算出し、グラフにプロットしました。
決定係数R2が最大となる説明変数の割合0.7を選択します。
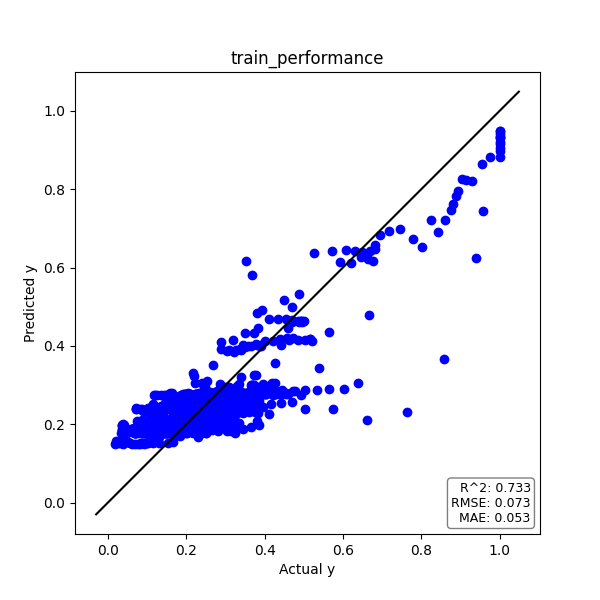
トレーニングデータ
実測値yと予測値のプロット、そして時系列プロットは下図の通りです。
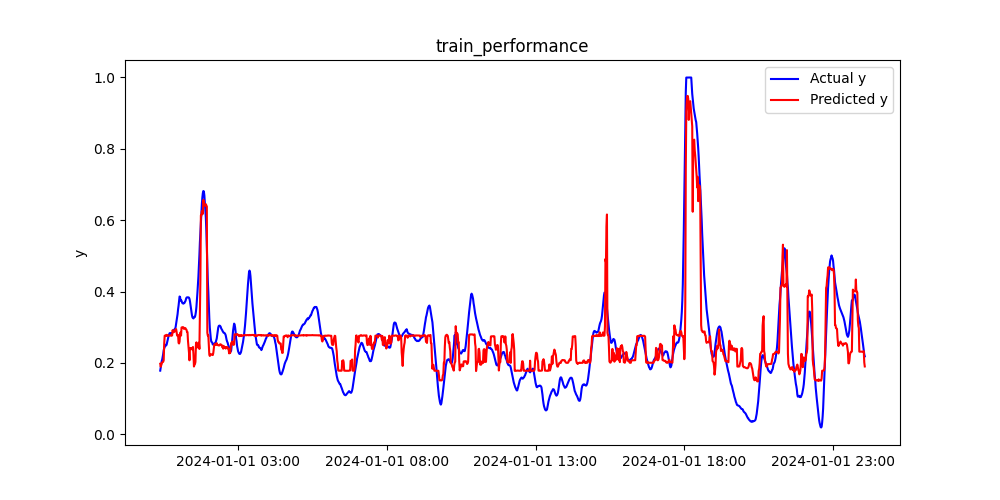
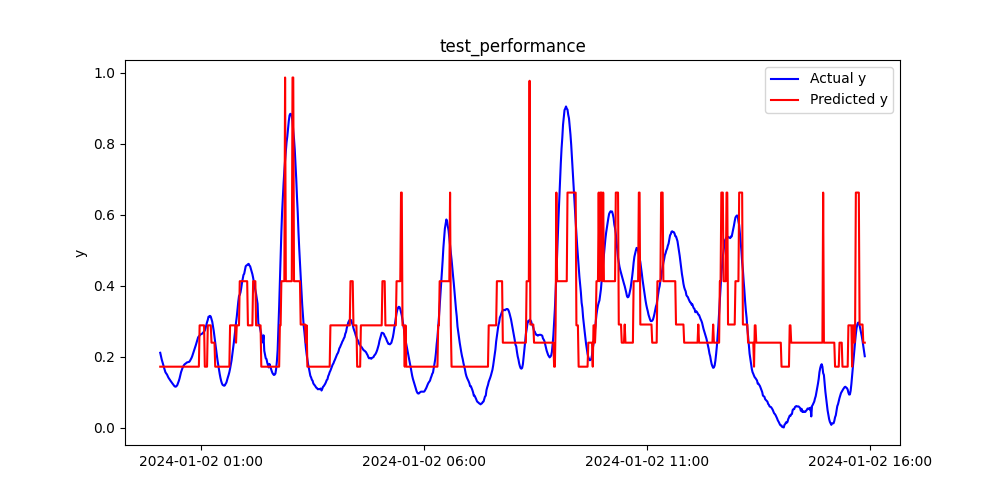
テストデータ
実測値yと予測値のプロット、そして時系列プロットは下図の通りです。
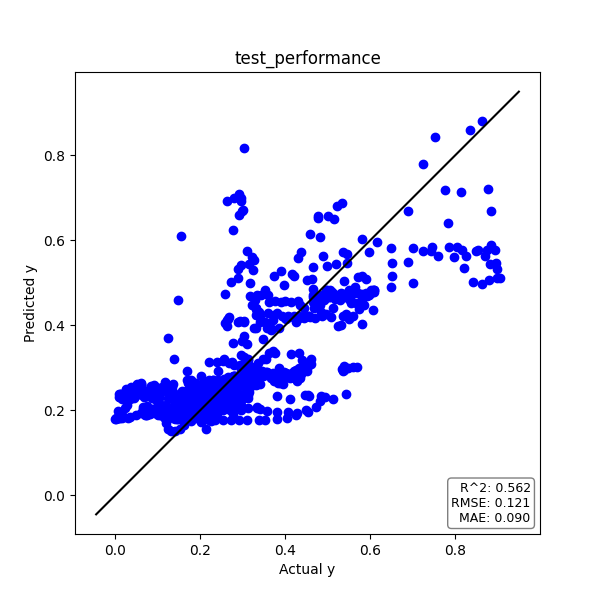
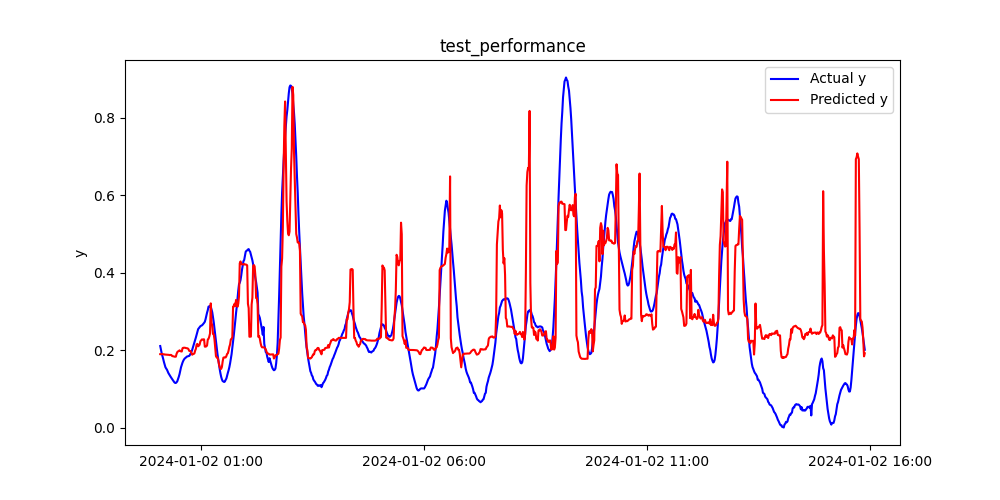
参考文献
実験計画法の教科書と思われますが、決定木やランダムフォレストの回帰分析についても解説しています。
決定木やランダムフォレストは分類でよく使われるため、回帰に重点を置いて解説されている書籍は少ないので大変重宝しました。
