どうも。こんにちは。
ケミカルエンジニアのこーしです。
本日は、「部分的最小二乗回帰(PLS)」についてわかりやすく解説します。
線形回帰モデルとして現場でよく使われているPLSについて、簡単に解説しつつ、実際に回帰モデルを作成するPythonコードをご紹介します。
本記事を読むことで、PLSについて理解が深まり、実際のデータ解析でPLSを使いこなすことができるようになります!
本記事の内容
・部分的最小二乗回帰(PLS)とは
・サンプルデータの入手
・【Python】PLSによる回帰分析
・回帰分析結果
・参考文献
目次
部分的最小二乗回帰(PLS)とは
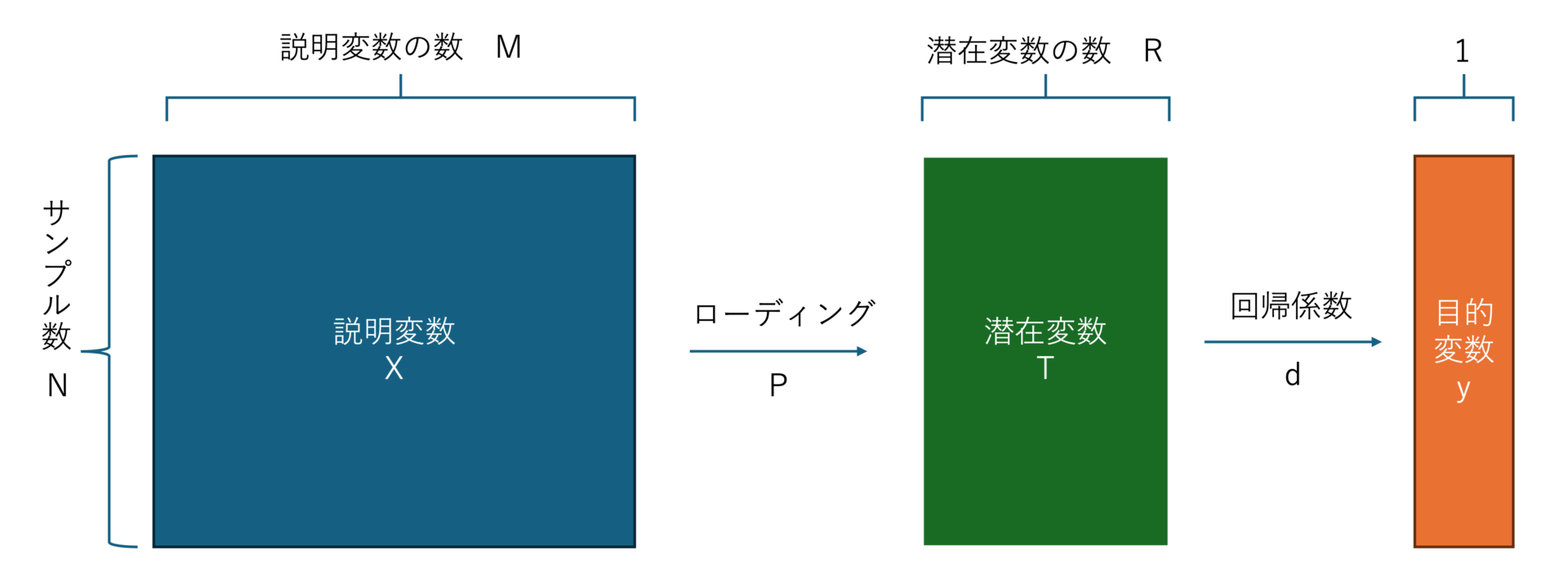
部分的最小二乗回帰(PLS)は、説明変数\(X\)の線形結合で潜在変数\(T\)を導出し、その潜在変数\(T\)の線形結合で目的変数\(y\)を表現します。
潜在変数\(T\)は、潜在変数と目的変数の共分散が最大になるように決定します。
$$\boldsymbol{X} = \boldsymbol{T}\boldsymbol{P}^\top + \boldsymbol{E} = \sum_{r=1}^{R}\boldsymbol{t_{r}}\boldsymbol{p_{r}}^\top + \boldsymbol{E} \tag{1}$$
$$\boldsymbol{y} = \boldsymbol{Td} + \boldsymbol{f} = \sum_{r=1}^{R}d_r\boldsymbol{T_r} + \boldsymbol{f}\tag{2}$$
記号の説明
- \(\boldsymbol{t}_r \in \mathbb{R}^N\):潜在変数ベクトル
- \(\boldsymbol{T} \in \mathbb{R}^{N\times R}\):潜在変数行列
- \(\boldsymbol{p}_r \in \mathbb{R}^M\):ローディングベクトル
- \(\boldsymbol{P} \in \mathbb{R}^{M \times R}\):ローディング行列
- \(\boldsymbol{d} \in \mathbb{R}^R\):回帰係数
- \(\boldsymbol{E} \in \mathbb{R}^{N \times M}\):誤差
- \(\boldsymbol{f} \in \mathbb{R}^N\):誤差
PLSのポイント
- PLSは、線形回帰分析手法の一つ
- 説明変数(X)間の相関関係(多重共線性)にも対応可能
- 説明変数(X)の数よりサンプル数が少なくても計算可能
- 目的変数(y)と説明変数(X)の相関関係を考慮するので、主成分回帰(PCR)より精度が出やすい
PLSは、潜在変数を用いることで「多重共線性」の問題に対応しています。
また、下記2点の特徴があるため、後述する主成分回帰(PCR)とリッジ回帰よりも優れていると言えます。
①説明変数と目的変数の間の相関関係も考慮(より予測精度が出やすい)
②説明変数の数よりもサンプル数が少なくても回帰係数を計算できる
よって、PLSは線形回帰分析手法の中で特に使い勝手が良く、あらゆる場面で活用されています。
多重共線性とは
重回帰分析では、「多重共線性」に注意が必要です。
説明変数(X)間に相関関係がある場合、最小二乗法で回帰係数を求めようとすると、回帰係数の値がわずかな測定ノイズの違いで大きくばらついてしまいます。
この現象を「多重共線性」と呼びます。
そこで、多重共線性の問題を解決するために、「主成分回帰(PCR)」、「リッジ回帰」という回帰分析手法が用いられます。
主成分回帰(PCR)
PCRは、主成分分析を回帰分析に応用した手法です。
まず、説明変数が無相関になるように、説明変数に主成分分析(PCA)を適用します。
そして、PCAによって得られた主成分得点を入力とし、最小二乗法により回帰係数を求めます。
PCRは、多重共線性の問題は解決できますが、下記2点の理由により予測精度が出にくいというデメリットがあります。
- PCAにより次元削減を行っているため、大量の情報を捨ててしまう
- PCAによる主成分の導出では、説明変数しか考慮しておらず、目的変数yも考慮すべき
リッジ回帰
多重共線性を防ぐもう一つの回帰分析手法は、リッジ回帰です。
リッジ回帰は、回帰係数の大きさにペナルティを設けることで、逆行列計算を安定化させ、相関関係にある説明変数でも安定した回帰係数が得られます。
一方、デメリットは、説明変数(X)の数よりサンプル数が少ないと回帰係数が計算できないということです。
PLSの回帰モデル
PLSの回帰モデルは下式のように表せます。
$$\boldsymbol{y} = \boldsymbol{X}\boldsymbol{\beta}_{pls} + \boldsymbol{f^{\prime}}\tag{3}$$
$$\boldsymbol{\beta}_{pls} = \boldsymbol{W}\Bigl(\boldsymbol{P}^\top \boldsymbol{W}\Bigr)^{-1}\boldsymbol{d}\tag{4}$$
記号の説明
- \(\boldsymbol{W} \in \mathbb{R}^{M\times R}\):重み行列
- \(\boldsymbol{\beta_{pls}} \in \mathbb{R}^M\):回帰係数
- \(\boldsymbol{f^{\prime}} \in \mathbb{R}^N\):誤差
どの教科書も、(4)式の証明は省略しているようです。
しかし、下記のブログに証明があるのを見つけたので、ぜひ参考にしてみてください。
部分的最小二乗回帰(Partial Least Squares Regression, PLS)の回帰係数の証明
また、回帰係数を求めるアルゴリズムには、NIPALSとSIMPLSの2種類があります。
アルゴリズムを詳しく解説すると長くなってしまうため、気が向いたら別記事で解説します。
本記事では、Pythonのscikit-learnで回帰係数を求めます。
ちなみに、scikit-learnでは特異値分解(SVD)に基づいたSIMPLSアルゴリズムを採用しています。
サンプルデータの入手
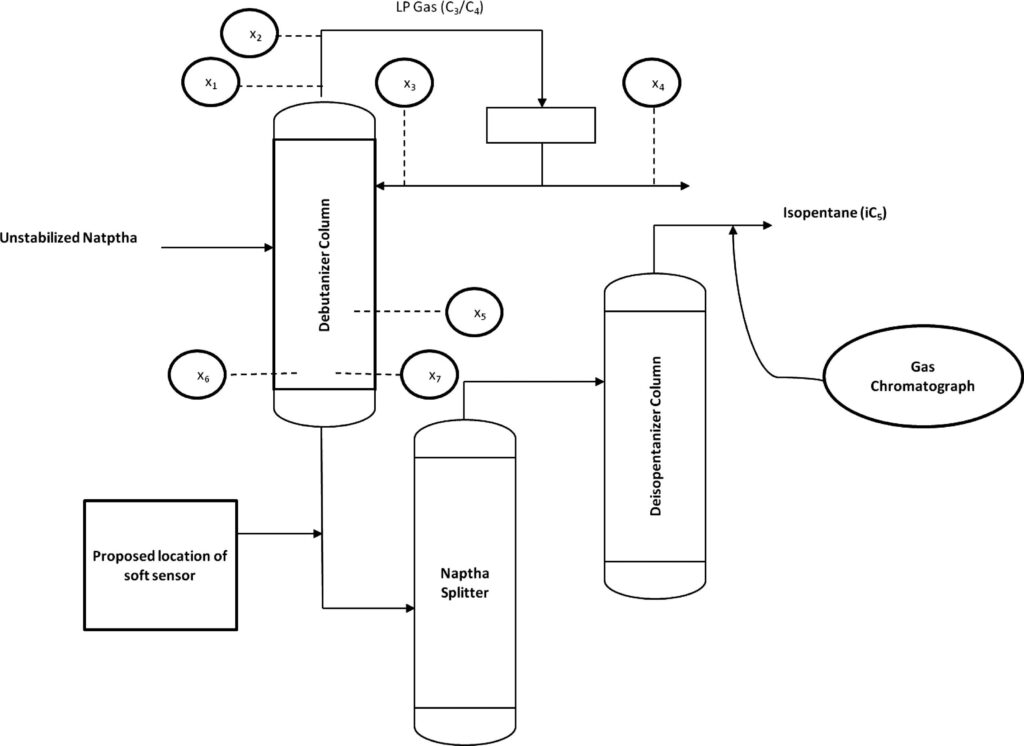
コチラのGitHubページで入手できる「debutanizer_data.csv」を利用します。
脱ブタン塔のプロセスデータであり、プロセスフローは上図の通りです。
説明変数がx1〜x7の7個で、目的変数がyの1個、サンプル数は2394個です。
| 変数名 | 詳細 | 日本語訳 |
|---|---|---|
| x1 | Top Temperature | 塔頂温度 |
| x2 | Top pressure | 塔頂圧力 |
| x3 | Reflux flow | 還流流量 |
| x4 | Flow to next process | 次プロセスへの流量 |
| x5 | 6th tray Temperature | 6段目温度 |
| x6 | Bottom Temperature1 | 塔底温度1 |
| x7 | Bottom Temperature2 | 塔底温度2 |
| y | Butane(C4) content in the debutanizer column bottom | 塔底におけるブタン含有量 |
データの読み込み
「debutanizer_data.csv」と同じフォルダに、「pls_regression.ipynb」(pls_regression.pyでも可)というファイルを作成しましょう。
下記のコードでライブラリのインポートと、データの読み込みを行います。
そして、下記3つのデータの前処理を行います。
- 時系列データなので、実務を想定しインデックスに時刻を割り振ります。
- 目的変数yの測定時間を考慮し、5分(行)だけデータをずらしておきます。
- プロセス知見より、目的変数yと説明変数x1〜x7の時間差を18分とします(時間遅れ変数の作成)。
import pandas as pd import numpy as np import matplotlib.pyplot as plt import matplotlib.dates as mdates from sklearn import metrics from sklearn.model_selection import train_test_split, cross_val_predict from sklearn.preprocessing import StandardScaler from sklearn.cross_decomposition import PLSRegression
#脱ブタン塔のプロセスデータを読み込む
df = pd.read_csv('debutanizer_data.csv')
#時系列データなので、実務データを想定しindexに時刻を割り当てる
# 開始日時を指定
start_datetime = '2024-01-01 00:00:00'
# DataFrameの長さを取得
n = len(df)
# 日時インデックスを生成(1分間隔)
date_index = pd.date_range(start=start_datetime, periods=n, freq='T')
# DataFrameのインデックスを新しい日時インデックスに設定
df.index = date_index
# 目的変数の測定時間を考慮(5分間)
df['y'] = df['y'].shift(5)
#yがnanとなる期間のデータを削除
df = df.dropna()
# 説明変数Xと目的変数yに分割
X = df.iloc[:, :-1]
y = df.iloc[:, -1]
#時間遅れ変数を作成
delay_number = 18
X_with_delays = pd.DataFrame()
for col in X.columns:
col_name = f"{col}_delay_{delay_number}"
X_with_delays[col_name] = X[col].shift(delay_number)
# 時間遅れ変数とyのデータフレームを作成
X_with_delays['y'] = y
X_with_delays = X_with_delays.dropna()
# 目的変数と説明変数に分割
X = X_with_delays.iloc[:, :-1]
y = X_with_delays['y']
【Python】PLSによる回帰分析
サンプルデータを読み込んだら、PLSの回帰モデルを作成していきましょう。
下記の書籍を参考にしてpythonコードを作成しました。
化学のためのPythonによるデータ解析・機械学習入門(改訂2版)
まず、下記3つのモジュールを作成します。
- evaluate_performance
- evaluate_model
- perform_pls_regression
def evaluate_performance(X, y, y_train, model, save_to_csv=False, filename='performance.csv'):
"""
モデルの性能を評価し、結果をプロットします。
オプションで予測結果をCSVファイルに保存します。
Parameters:
X : pd.DataFrame
説明変数のデータセット
y : pd.Series
目的変数の値
y_train : pd.Series
トレーニングデータの目的変数(標準化解除に使用)
model : sklearn model
評価する訓練済みのモデル
save_to_csv : bool, optional
結果をCSVファイルに保存するかどうかを指定 (default is False)
filename : str, optional
出力するCSVファイルの名前 (default is 'performance.csv')
Returns:
r2 : 決定係数R^2
rmse : RMSE
mae : MAE
"""
# yの推定値を算出
y_pred = model.predict(X) * y_train.std() + y_train.mean()
# 性能指標の算出
r2 = metrics.r2_score(y, y_pred)
rmse = np.sqrt(metrics.mean_squared_error(y, y_pred))
mae = metrics.mean_absolute_error(y, y_pred)
print(f"R^2: {r2:.3f}, RMSE: {rmse:.3f}, MAE: {mae:.3f}")
# プロットの作成
plt.figure(figsize=(6, 6))
plt.scatter(y, y_pred, color='blue')
y_max = max(y.max(), y_pred.max())
y_min = min(y.min(), y_pred.min())
# 取得した最小値-5%から最大値+5%まで、対角線を作成
plt.plot([y_min - 0.05 * (y_max - y_min), y_max + 0.05 * (y_max - y_min)],
[y_min - 0.05 * (y_max - y_min), y_max + 0.05 * (y_max - y_min)], 'k-')
plt.ylim(y_min - 0.05 * (y_max - y_min), y_max + 0.05 * (y_max - y_min))
plt.xlim(y_min - 0.05 * (y_max - y_min), y_max + 0.05 * (y_max - y_min))
plt.xlabel('Actual y')
plt.ylabel('Predicted y')
# テキストボックスを右下に配置
plt.text(0.98, 0.02, f'R^2: {r2:.3f}\nRMSE: {rmse:.3f}\nMAE: {mae:.3f}', transform=plt.gca().transAxes,
fontsize=9, verticalalignment='bottom', horizontalalignment='right',
bbox=dict(boxstyle="round,pad=0.3", edgecolor='black', facecolor='white', alpha=0.5))
plt.title(filename[:-4])
plt.grid(False)
plt.axis('equal')
plt.show()
# 時系列のプロット
plt.figure(figsize=(10, 5))
plt.gca().xaxis.set_major_formatter(mdates.DateFormatter('%Y-%m-%d %H:%M')) # 日時形式を設定
plt.gca().xaxis.set_major_locator(mdates.HourLocator(interval=5)) # 4時間ごとに目盛りを設定
plt.plot(y.index, y, label='Actual y', color='blue', marker='', linestyle='-')
plt.plot(y.index, y_pred, label='Predicted y', color='red', marker='', linestyle='-')
#plt.gcf().autofmt_xdate() # x軸のラベルを自動で斜めにして読みやすくする
plt.ylabel('y')
plt.title(filename[:-4])
plt.legend()
plt.show()
# データの保存
if save_to_csv:
results_df = pd.DataFrame({
'Actual': y,
'Predicted': y_pred.flatten(),
'Error': y - y_pred.flatten()
})
results_df.to_csv(filename, index=False)
print(f"Data saved to {filename}")
return r2, rmse, mae
def evaluate_model(X_train_scaled, y_train, X_test_scaled, y_test, model, save_csv=False, train_filename='train_performance.csv', test_filename='test_performance.csv'):
"""
トレーニングデータとテストデータの両方でモデルの性能を評価します。
Parameters:
X_train_scaled : pd.DataFrame
標準化されたトレーニングデータの説明変数
y_train : pd.Series
トレーニングデータの目的変数
X_test_scaled : pd.DataFrame
標準化されたテストデータの説明変数
y_test : pd.Series
テストデータの目的変数
model : sklearn model
評価する訓練済みのモデル
save_csv : bool, optional
結果をCSVファイルに保存するかどうかを指定 (default is False)
train_filename : str, optional
トレーニングデータの予測結果を保存するCSVファイルの名前 (default is 'train_performance.csv')
test_filename : str, optional
テストデータの予測結果を保存するCSVファイルの名前 (default is 'test_performance.csv')
"""
print("Evaluating Training Data")
evaluate_performance(X_train_scaled, y_train, y_train, model, save_to_csv=save_csv, filename=train_filename)
print("Evaluating Test Data")
evaluate_performance(X_test_scaled, y_test, y_train, model, save_to_csv=save_csv, filename=test_filename)
def perform_pls_regression(X, y, fold_number=5, test_size=0.4, shuffle=False):
"""
PLS回帰モデルを構築し、クロスバリデーションを用いて最適な主成分数を決定します。
その後、最適な主成分数でモデルを再構築し、訓練データとテストデータの性能を評価します。
Parameters:
X : pd.DataFrame
説明変数のデータセット
y : pd.Series
目的変数のデータ
fold_number : int, optional
クロスバリデーションで使用するフォールドの数 (default is 5)。
test_size : float, optional
データを分割する際のテストデータの割合 (default is 0.4)。
shuffle : bool, optional
データ分割時にデータをシャッフルするかどうか (default is False)。
Returns:
best_components : 最適な主成分数
standard_regression_coefficients : 標準回帰係数
beta_train : 回帰係数
intercept_train : 切片
"""
# データの分割
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=test_size, shuffle=shuffle, random_state=0)
# データの標準化
scaler = StandardScaler()
X_train_scaled = scaler.fit_transform(X_train)
X_test_scaled = scaler.transform(X_test)
y_train_scaled = scaler.fit_transform(y_train.values.reshape(-1, 1)).ravel()
# 主成分数を決定するためのクロスバリデーション
max_components = X_train.shape[1]
r2_scores = []
for n_components in range(1, max_components + 1):
pls = PLSRegression(n_components=n_components)
y_cv = cross_val_predict(pls, X_train_scaled, y_train_scaled, cv=fold_number)
r2 = metrics.r2_score(y_train_scaled, y_cv)
r2_scores.append((n_components, r2))
# r2_scoresをグラフで表示
components = [item[0] for item in r2_scores]
r2_values = [item[1] for item in r2_scores]
plt.figure(figsize=(8, 5))
plt.plot(components, r2_values, marker='o', linestyle='-', color='b')
plt.xlabel('Number of Components')
plt.ylabel('R2 Score (CV)')
plt.grid(True)
plt.show()
# 最適な主成分数の決定
best_components = max(r2_scores, key=lambda item: item[1])[0]
# 最適な主成分数で再度PLSモデルを作成
pls_final = PLSRegression(n_components=best_components)
pls_final.fit(X_train_scaled, y_train_scaled)
# 標準回帰係数の取得
standard_regression_coefficients = pd.DataFrame(pls_final.coef_, index=X_train.columns,
columns=['Standard Regression Coefficients'])
# 回帰係数、切片の算出
std_X_train = X_train.std()
std_y_train = y_train.std()
beta_train = std_y_train * standard_regression_coefficients.iloc[:, 0] / std_X_train
intercept_train = y_train.mean() - X_train.mean() @ beta_train
evaluate_model(X_train_scaled, y_train, X_test_scaled, y_test, model=pls_final)
return best_components, standard_regression_coefficients, beta_train, intercept_train
最後にperform_pls_regressionモジュールを実行します。
# 関数の実行
best_components, standard_regression_coefficients, beta_train, intercept_train = perform_pls_regression(X, y)
print(f"Optimal number of components: {best_components}")
print("Standard regression coefficients:")
print(standard_regression_coefficients)
print("Regression coefficients:")
print(beta_train)
print("Intercept:")
print(intercept_train)
回帰分析結果
上述のPythonコードによる回帰分析の結果を示します。
| PLS | R2 | RMSE | MAE |
| トレーニングデータ | 0.618 | 0.087 | 0.062 |
| テストデータ | 0.551 | 0.122 | 0.088 |
それでは具体的に結果を見ていきましょう。
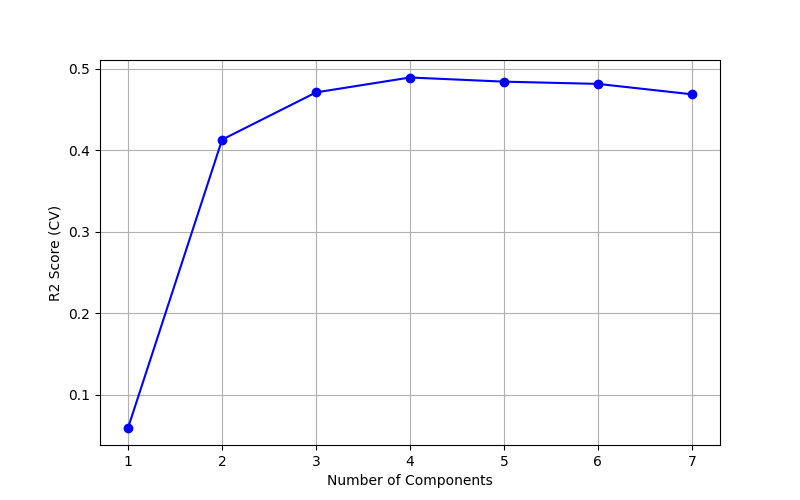
CVによる主成分数の決定
主成分数(潜在変数の数:Number of Components)を変化させ、クロスバリデーションにより決定係数R2を算出し、グラフにプロットしました。
決定係数R2が最大となる主成分数4を選択します。
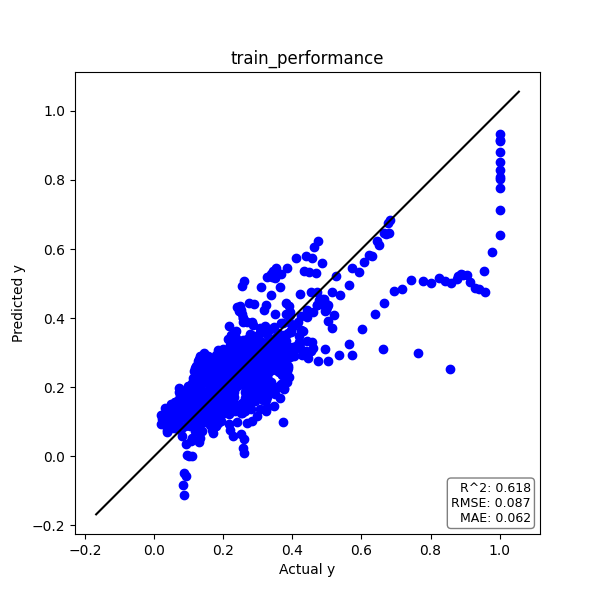
トレーニングデータ
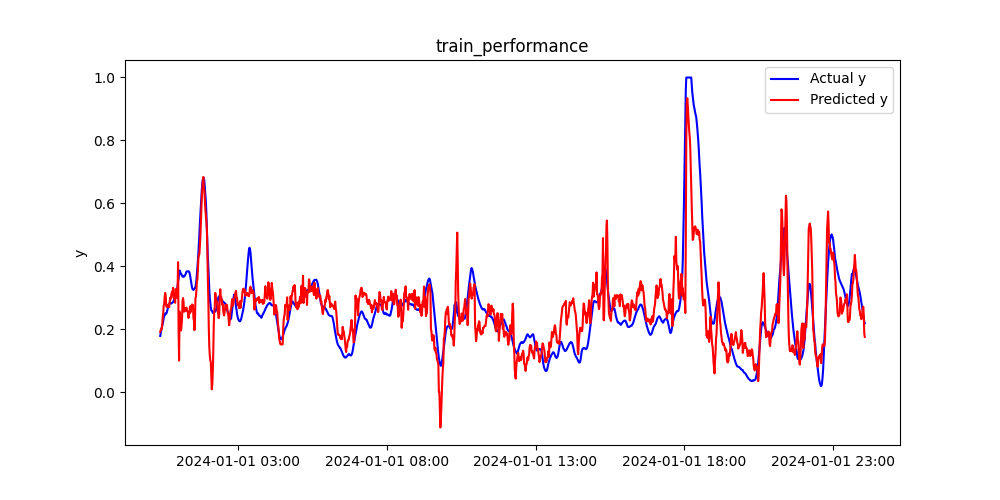
実測値yと予測値のプロットは下図の通りです。
プロットが対角線上に乗れば、精度良く推定できていると言えます。
また、予測精度の評価指標である決定係数R2とRMSE、MAEをグラフ中に記載しています。
また、時系列プロットも下図に示しました。
テストデータ
トレーニングデータと同様に、テストデータについても見てみましょう。
実測値yと予測値のプロット、そして時系列プロットは下図の通りです。
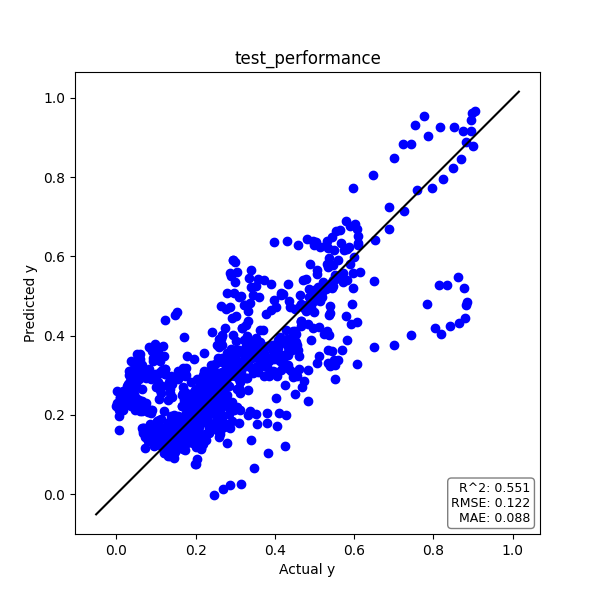
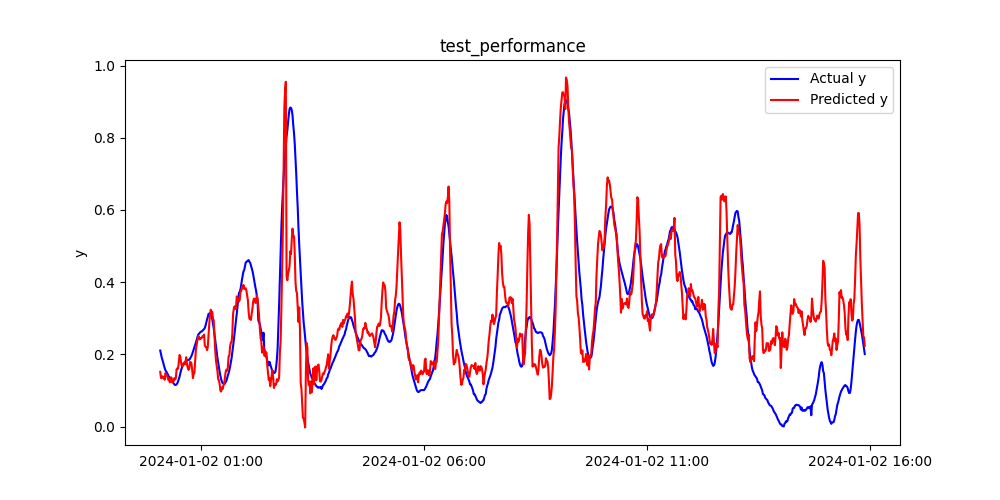
トレーニングデータとほぼ同等の予測精度が出ました。
過学習していると、トレーニングデータは予測精度が良いのに、テストデータでは全然精度が出ないということがあります。
標準回帰係数
今回得られたPLSモデルの標準回帰係数は下表の通りです。
| 標準回帰係数 | |
| x1 | -0.005 |
| x2 | -0.049 |
| x3 | -0.183 |
| x4 | -0.087 |
| x5 | -0.928 |
| x6 | 0.205 |
| x7 | 0.215 |
標準回帰係数の正負の符号から、寄与の方向性がわかります。
また、標準回帰係数の絶対値の大きさからは、目的変数への寄与の大きさがわかります。
今回の例では、x1、x2、x3、x4、x5は符号が負になっており、特にx5は絶対値が最も大きく、最も寄与が大きいことがわかります。
得られた標準回帰係数の特徴を原理原則と照らし合わせ、大きく外れていないかチェックすることが重要です(モデルの解釈)。
回帰係数と切片
標準回帰係数を元の単位に戻し、回帰係数と切片を算出しました。
下表の回帰係数を使えば、今後新しいデータ(説明変数)が得られた際に、いちいち標準化せずに予測値を得ることができます。
| 回帰係数/切片 | |
| x1 | -0.008 |
| x2 | 0.230 |
| x3 | -0.119 |
| x4 | -0.104 |
| x5 | -1.313 |
| x6 | 0.212 |
| x7 | 0.204 |
| 切片 | 0.858 |
まとめ
今回、脱ブタン塔のプロセスデータを用いて、PythonでPLSモデルを作成し、回帰モデルの予測精度も評価しました。
PLSは線形回帰モデルであるため、結果(標準回帰係数)の解釈が容易であり、とても使いやすいモデルです。
データによって相性はあるかもしれませんが、PLSは比較対象としてもよく使われるため、PythonでPLSを実装できるようにしておくと非常に重宝すると思います!
参考文献
PLSの理論的な部分はこちらの書籍を参考にしました。
アルゴリズムの説明が詳しく、PLSを真に理解したい方にオススメです。
絶版本ですが、どの教科書もこの書籍を参考文献にあげています。
PLSやニューラルネットワークの解説があり、1995年に出版された書籍ですが今なお読む価値がある本です。
図書館などで探してみると良いと思います。
化学のためのPythonによるデータ解析・機械学習入門(改訂2版)
pythonコードはこちらの書籍を参考にしました。
化学系でデータ解析をするならば、必ず手元に置いておきたい1冊です。
誤植も少なく、すぐにプログラムを動かすことができます。
