どうも。こんにちは。
ケミカルエンジニアのこーしです。
本日は、「回帰モデルの残差分析(回帰診断法)」についてわかりやすく解説します。
回帰分析は、皆さん一度は実施したことがあると思います。
しかし、決定係数(R2)や二乗平均平方根誤差(RMSE)のみをチェックして、モデルの精度を判断しているのではないでしょうか。
実は、予測値と実測値の差である「残差」には貴重な情報が隠されています。
本記事では、「アンスコムの数値例」を用いて、残差分析で得られる貴重な情報について解説してみます。
回帰分析の精度向上に頭を悩ませている方は、ぜひ読んでみてください。
本記事の内容
・残差分析とは
・残差分析の種類
・アンスコムの数値例
・参考文献
この記事を書いた人

こーし(@mimikousi)
目次
残差分析とは
残差分析とは、線形回帰モデルを使ってデータ分析をする際、モデルの予測精度や仮定の妥当性をチェックする重要な手法です。
線形回帰では、データに合わせて直線を引いて予測を行いますが、この予測は常に完璧ではありません。
誤差項\(\epsilon\)が必ず生じます。
$$Y = X\beta + \epsilon$$
モデルが正確であるためには、下記の仮定を満たす必要があります。
誤差項の仮定
- 外れ値が少ないこと
- 誤差が互いに独立していること
- 誤差が均一な分散を持つこと(等分散性)
- 誤差が正規分布に従うこと(正規性)
しかし、これらの仮定が満たされない場合、最小二乗法による予測は信頼できない結果をもたらす可能性があります。
そこで登場するのが残差分析(回帰診断法)です。
残差は、実測値と予測値の差で計算され、観測不可能な誤差項の”推測値”と見なせます。
この「残差」をグラフにプロットすることで、外れ値の存在や、誤差の等分散性や正規性が満たされているかどうかを視覚的に評価できます。
もし仮定が満たされていない場合は、モデルを修正したり、別の統計手法を検討するという判断ができます。
残差分析の種類
残差分析には、下記の通りいくつかの種類があります。
残差分析の種類
- 残差プロット
- 正規Q-Qプロット
- 標準化残差の絶対値の平方根プロット
- leverage(てこ比)とCookの距離
それでは、ひとつずつ詳しく見ていきましょう。
残差プロット
残差プロットには、いくつかの種類があります。
残差プロットの種類
- 時刻\(t\)を横軸にとり、残差\(e_{t}\)を縦軸にとってプロット(時系列データ)
- 予測値\(\widehat{y}_{i}\)を横軸にとり、点(\(\widehat{y}_{i}\), \(e_{i}\))をプロット
- 説明変数\(x_{i}\)を横軸にとり、点(\(x_{i}\), \(e_{i}\))をプロット
- 新しい説明変数\(x_{p+1, i}\)を横軸にとり、点(\(x_{p+1, i}\) , \(e_{i}\))をプロット
残差プロットもひとつずつ見ていきましょう。
1.時刻\(t\)を横軸にとり、残差\(e_{t}\)を縦軸にとってプロット
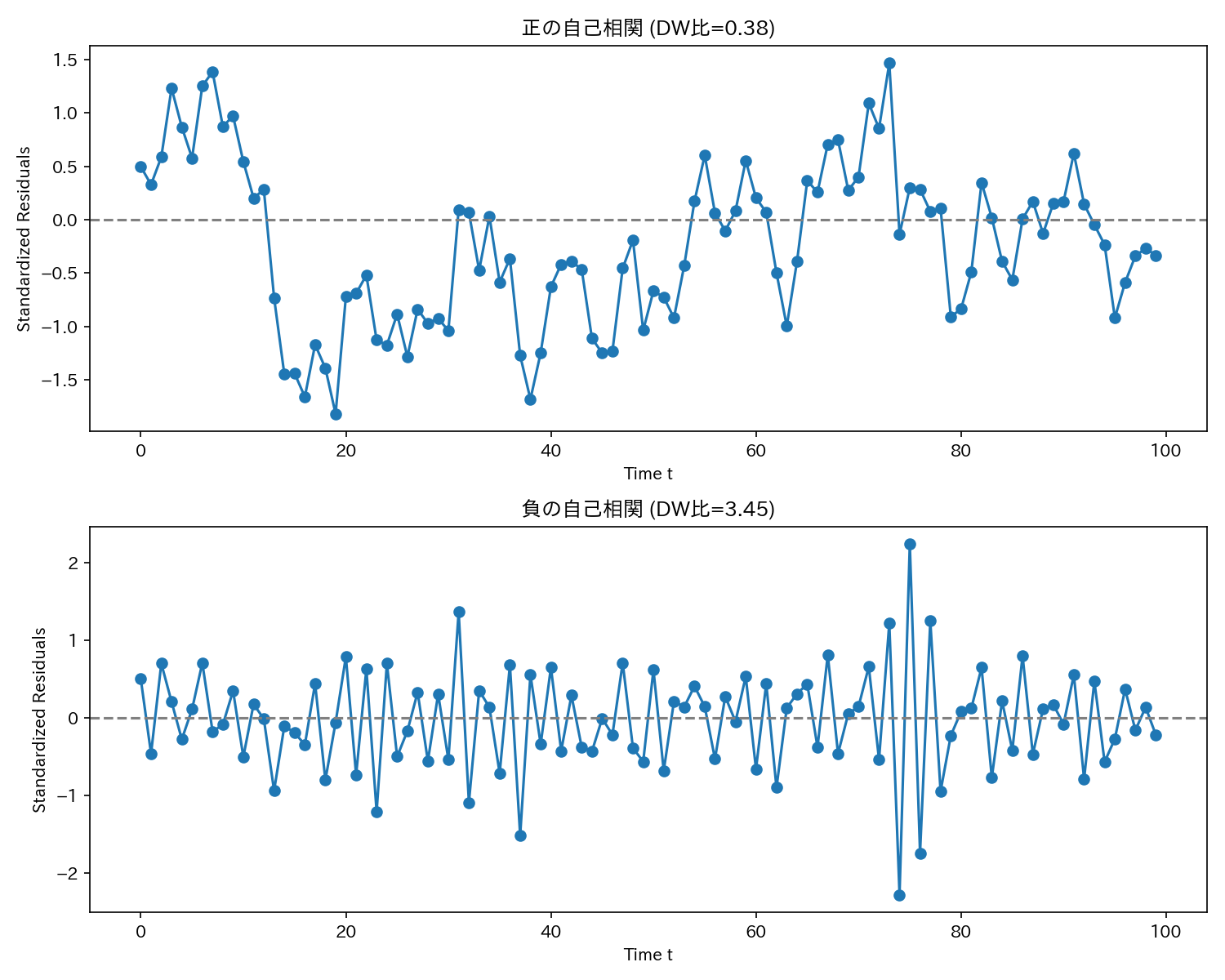
上図は、時系列データで最もよく使われる残差プロットです。
分散が均一かどうか(等分散性)が一目でよくわかります。
また、隣接した誤差項同士の相関(自己相関、もしくは系列相関)の有無も判断できます。
しかし、残差プロットから見た目で判断するのは、かなりの熟練を要するため、通常「ダービン・ワトソン(DW)比」を併用します。
DW比は0〜4の値をとり、2に近いと自己相関はないとされ、0に近いと正の自己相関、4に近いと負の自己相関があると判断できます。
上図は、DW比=0.38の正の自己相関のプロットと、DW=比3.45の負の自己相関のプロットです。
2.予測値\(\widehat{y}_{i}\)を横軸にとり、点(\(\widehat{y}_{i}\), \(e_{i}\))をプロット
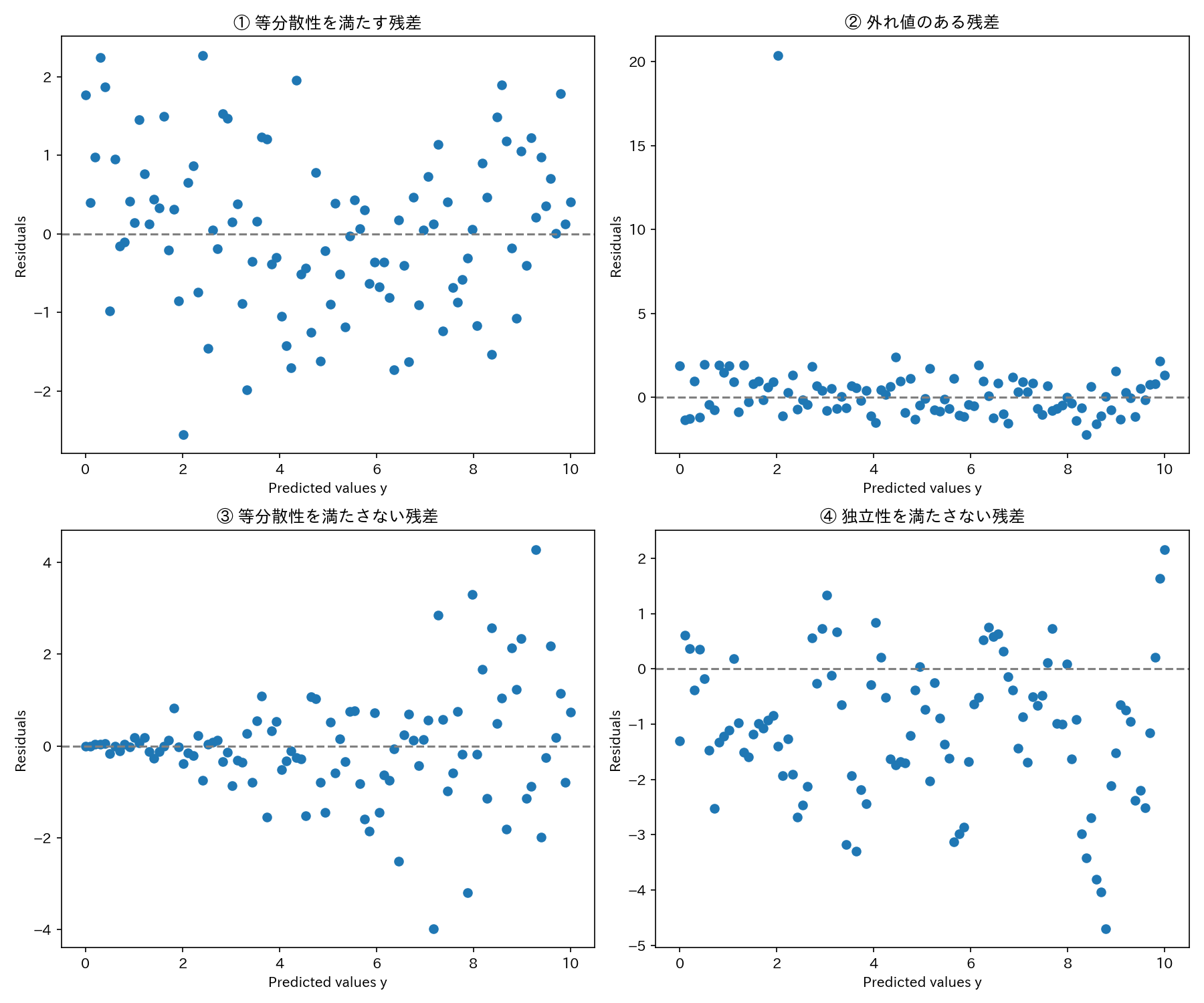
上図は、先述した「誤差項の仮定」を満たすかどうかを視覚的に判断できます。
今回は、下記4つの特徴を示す残差プロットを示しました。
残差の特徴
①等分散性を満たす
②外れ値がある
③等分散性を満たさない
④独立性を満たさない
3.説明変数\(x_{i}\)を横軸にとり、点(\(x_{i}\), \(e_{i}\))をプロット
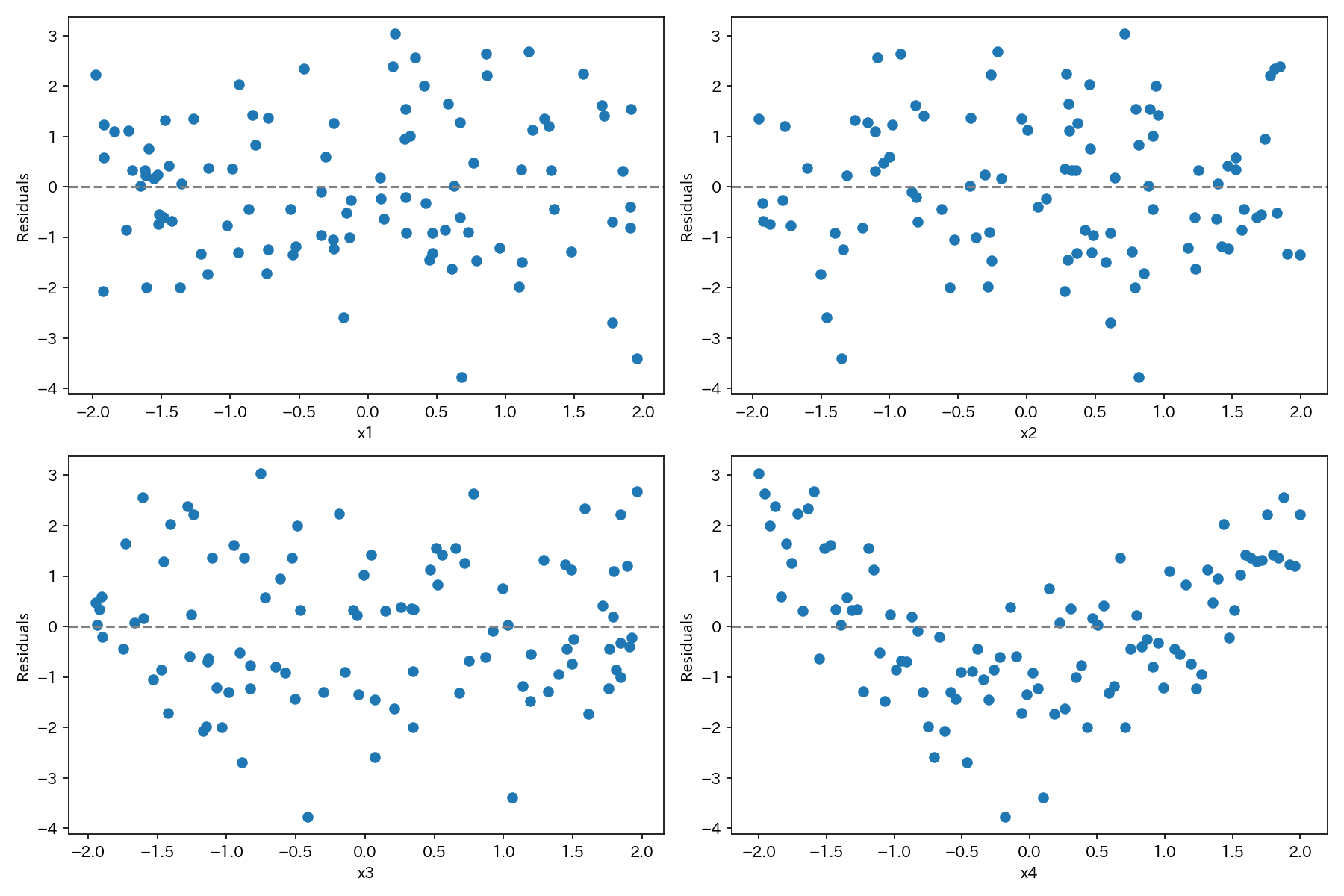
上図は、説明変数xの非線形性を調べるために最も効果的な残差プロットです。
もし、説明変数xとyの関係が非線形性であるならば、説明変数xと残差の間にも、しかるべき非線形の関係性が表れてきます。
上図の例では、x4と残差の間に非線形性の関係性が認められます。
4.新しい説明変数\(x_{p+1, i}\)を横軸にとり、点(\(x_{p+1, i}\) , \(e_{i}\))をプロット
新しい説明変数を追加するかどうかの判断として、この残差プロットが使えます。
もし、分散の増大傾向や減少傾向が認められれば、現行の回帰モデルでは、新しい説明変数によって説明される変動を捉えることができていないことを示します。
また、この残差プロットが非線形性を示す場合も、現行の回帰モデルでは、新しい説明変数に関する非線形な変動を捉えることができていないことを示します。
正規Q-Qプロット
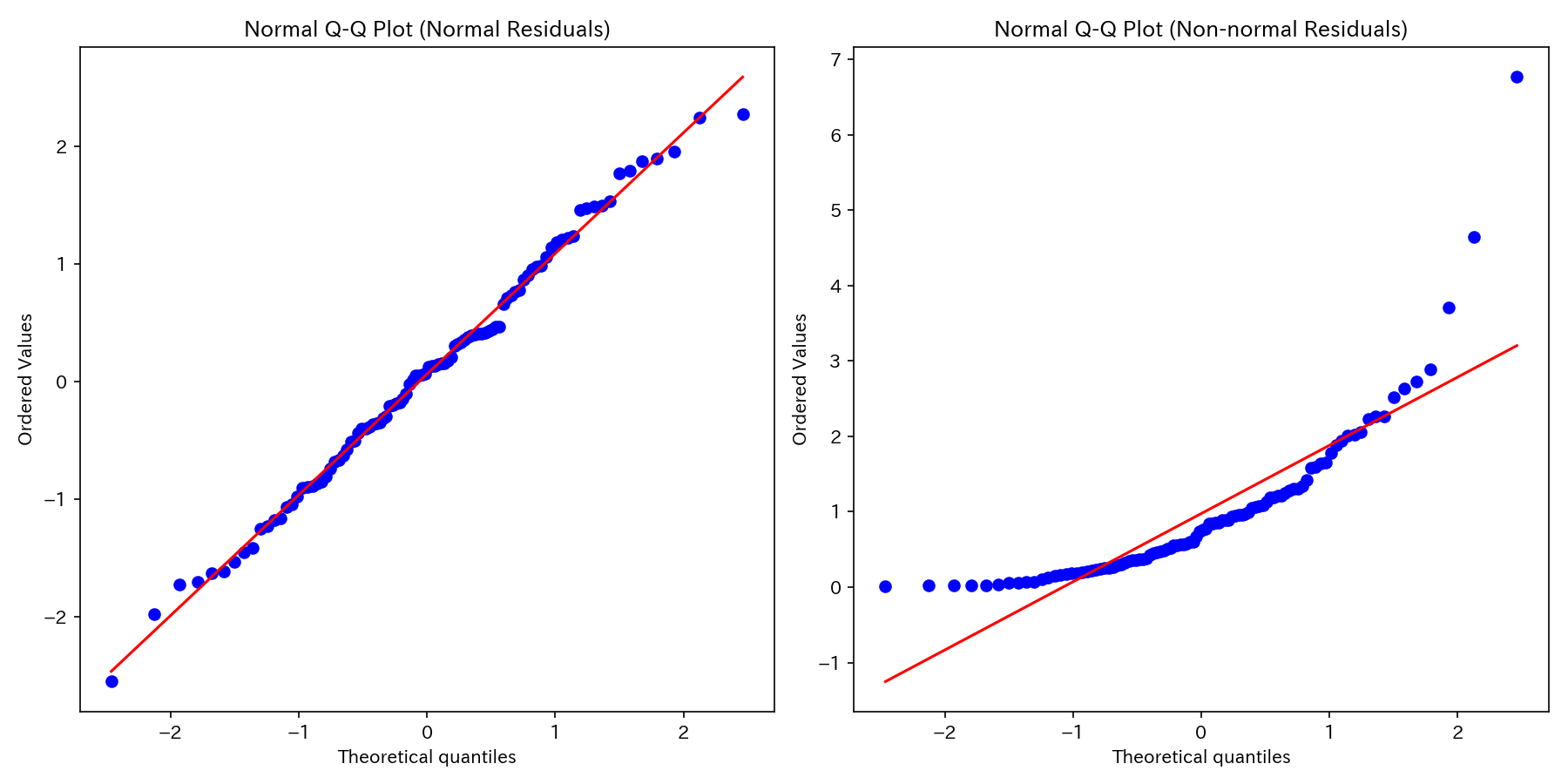
正規Q-Qプロットとは、残差を標準化し、小さい順に並べたものの分位点と、標準正規分布の累積分布関数の分位点をプロットしたものです。
誤差項の正規性の仮定が満たされているときは、プロットは傾き1の直線上に並びます。
よって、誤差項の正規性の仮定が妥当かどうかを判断できます。
上図は、正規性の仮定を満たす場合(左図)と満たさない場合(右図)の例です。
標準化残差の絶対値の平方根プロット
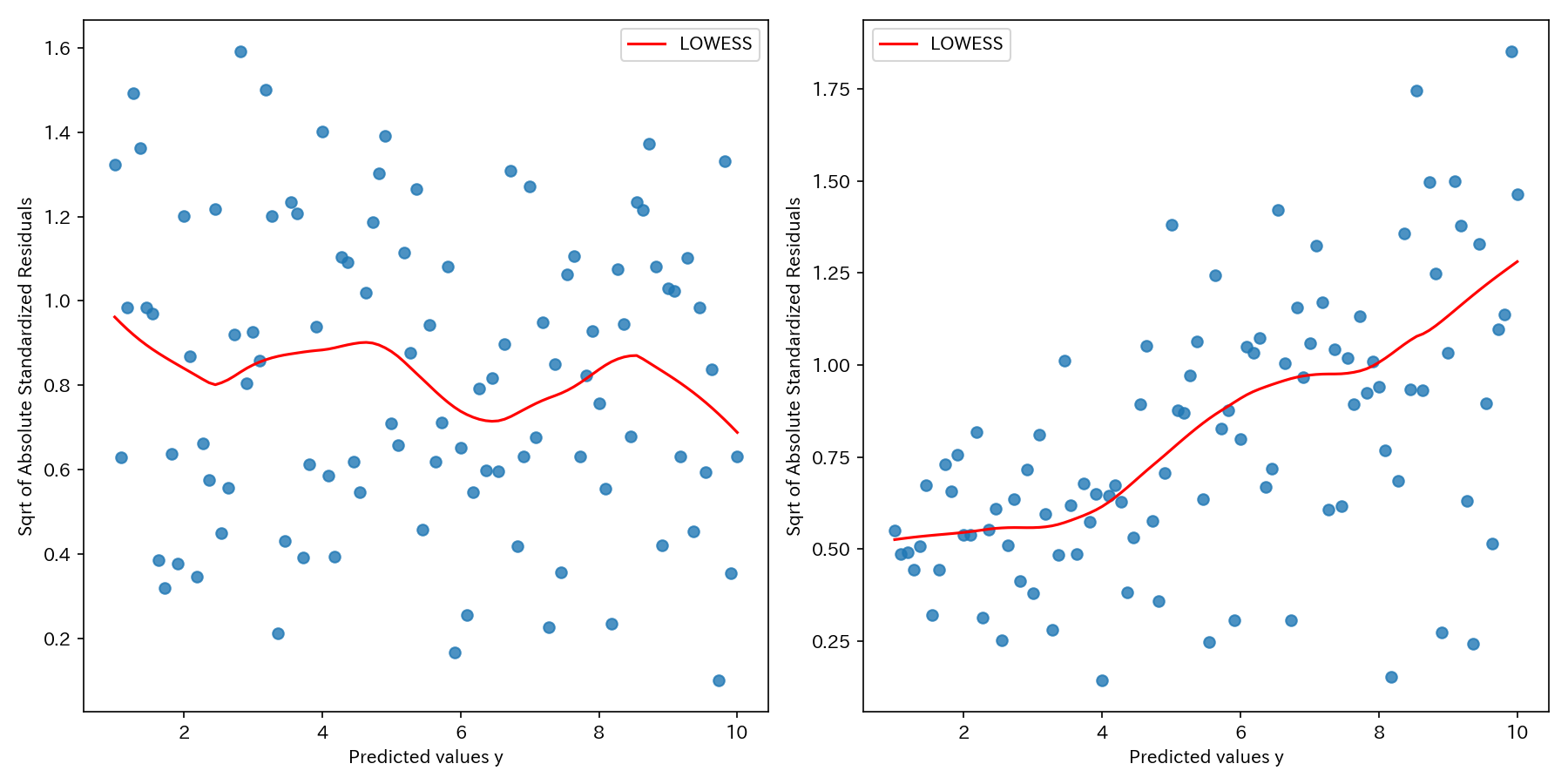
予測値\(\widehat{y}_{i}\)を横軸にとり、標準化残差の絶対値の平方根を縦軸にとってプロットします。
このプロットは、「残差の大きさ」に着目しており、特にプロットが予測値に対して増加または減少する傾向がある場合は、等分散性の仮定を満たしていないとより明確に判断できます。
上図は、等分散性の仮定を満たす場合(左図)と満たさない場合(右図)の例です。
leverage(てこ比)とCookの距離
n×pの説明変数行列\(X\)のランクが\(p\)であるとき、
$$\widehat{\beta} = (X^\top X)^{-1}X^\top y$$
は\(\beta\)の最小二乗推定量となります。そこで、
$$H = X(X^\top X)^{-1}X^\top = (h_{ij})$$
とおくと、予測値\(\widehat{y}\)は、下式のように書けます。
$$\widehat{y} = Hy$$
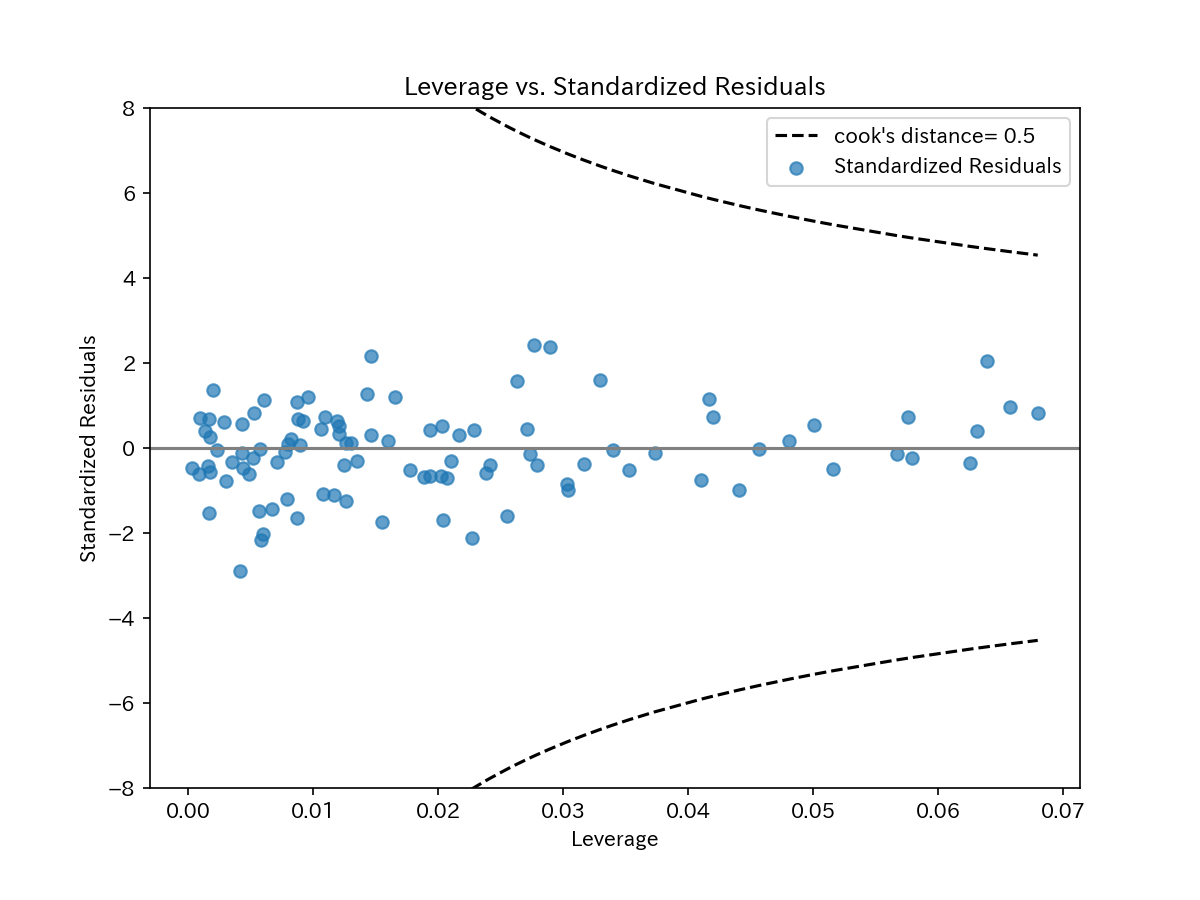
\(H = (h_{ij})\)は、ハット行列と呼ばれ、\(i\)番目の対角要素\(h_{ii}\)は\(i\)番目の観測値のleverage(てこ比)と呼ばれています。
てこ比は、各観測値の回帰係数への影響度を判断することができ、てこ比の大きい観測値はモデルへの影響力が大きいと判断し、ときには外れ値の候補となります。
よって、横軸にleverage(てこ比)をとり、縦軸に標準化残差をとってプロットします。
また、てこ比と共に示す値として、Cookの距離があります。
Cookの距離\(d_{i}\)は、下式のように表せます。
$$d_{i} = \frac{r_{i}^{2}}{p+1}\Bigl(\frac{h_{ii}}{1-h_{ii}}\Bigr)$$
Cookの距離は、全ての観測値を用いた場合の予測値と、\(i\)番目の観測値を除いた場合の予測値の差異に関する距離と考えられます。
てこ比と同様に、各観測値のモデルへの影響力を示し、0.5を超えると外れ値とされます。
【参考記事】
アンスコムの数値例
| X1 | Y1 | Y2 | Y3 | X2 | Y4 | |
| 1 | 10.0 | 8.04 | 9.14 | 7.46 | 8.0 | 6.58 |
| 2 | 8.0 | 6.95 | 8.14 | 6.77 | 8.0 | 5.76 |
| 3 | 13.0 | 7.58 | 8.74 | 12.74 | 8.0 | 7.71 |
| 4 | 9.0 | 8.81 | 8.77 | 7.11 | 8.0 | 8.84 |
| 5 | 11.0 | 8.33 | 9.26 | 7.81 | 8.0 | 8.47 |
| 6 | 14.0 | 9.96 | 8.10 | 8.84 | 8.0 | 7.04 |
| 7 | 6.0 | 7.24 | 6.13 | 6.08 | 8.0 | 5.25 |
| 8 | 4.0 | 4.26 | 3.10 | 5.39 | 19.0 | 12.50 |
| 9 | 12.0 | 10.84 | 9.13 | 8.15 | 8.0 | 5.56 |
| 10 | 7.0 | 4.82 | 7.26 | 6.42 | 8.0 | 7.91 |
| 11 | 5.0 | 5.68 | 4.74 | 5.73 | 8.0 | 6.89 |
【参考】新装版 回帰分析 P.132
上表は、残差分析の重要性を視覚的に確認できるアンスコムの数値例です。
アンスコムの数値例からは、4通りのプロットが得られます(うち3つの横軸はX1で共通)。
いずれのプロットも下式の回帰式となります。
$$y = 0.5x + 3.0$$
そして、決定係数も\(R^{2} = 0.67\)と同じになっています。
よって、これら4通りのプロットは推定結果からは見分けがつかないのです。
回帰プロット
では、実際どうなっているのか回帰プロットを見てみましょう。
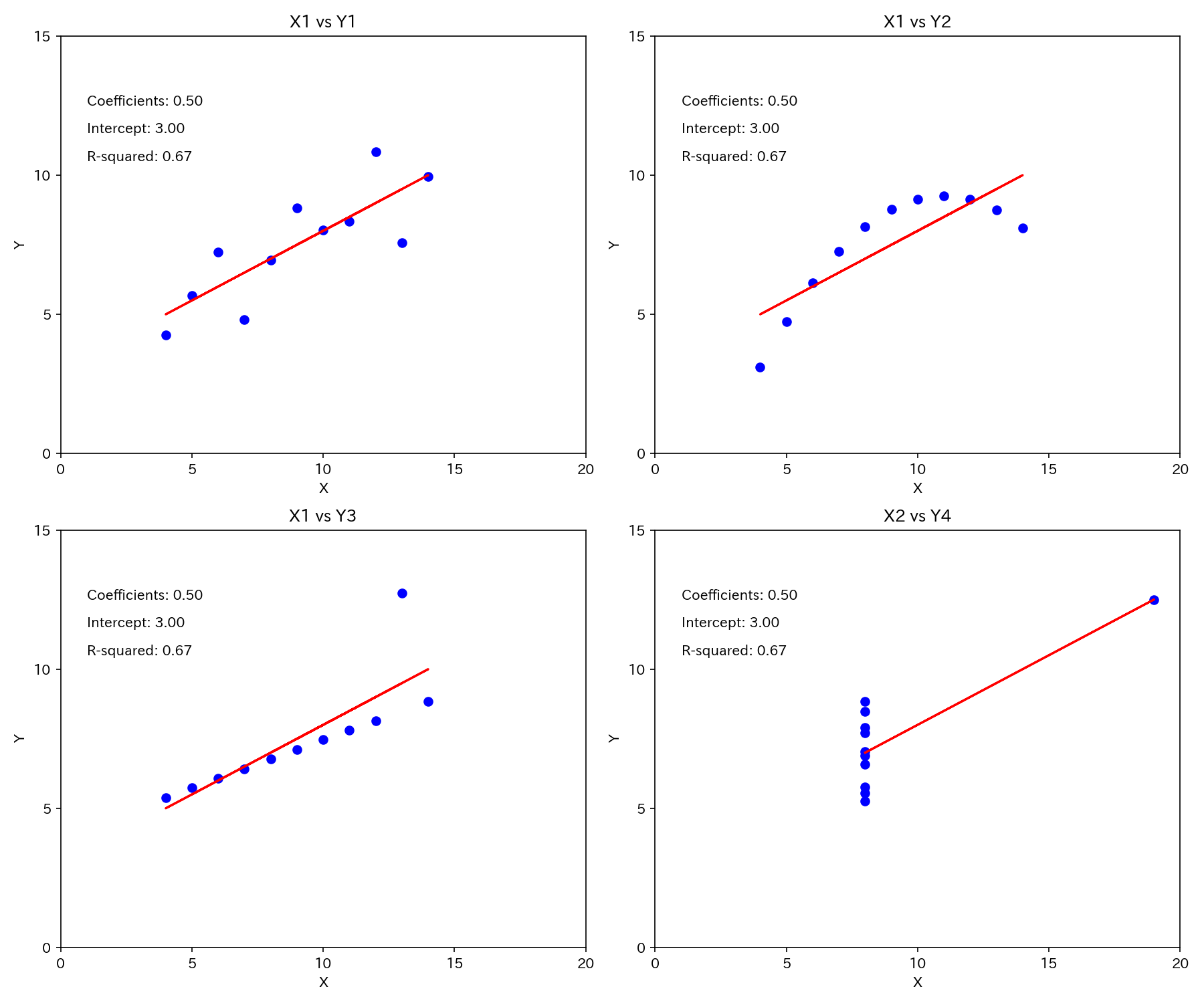
Y2は、非線形の関係性、Y3は、外れ値がありますね。
また、X2とY4のプロットは、本来回帰分析が不可能なデータであるのに、1点の外れたデータにより回帰できているように見える例です。
残差分析
それでは、残差分析をしてみます。
X1とY1
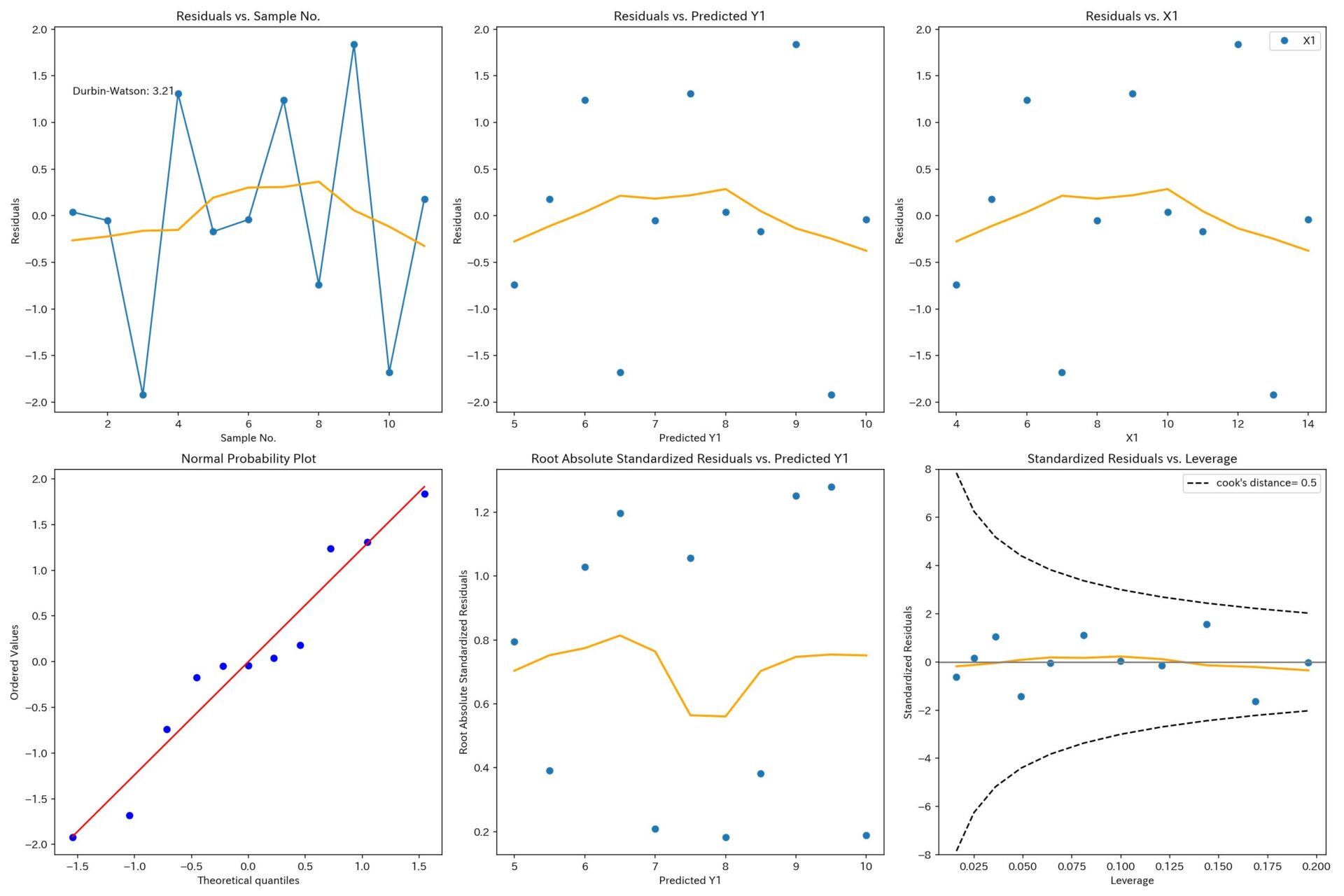
ダービン・ワトソン比が3.21と大きいのでやや負の自己相関のようです。
そのほかは、誤差項の等分散性、正規性の仮定も満たしているようですし、外れ値も見当たりません。
X1とY2
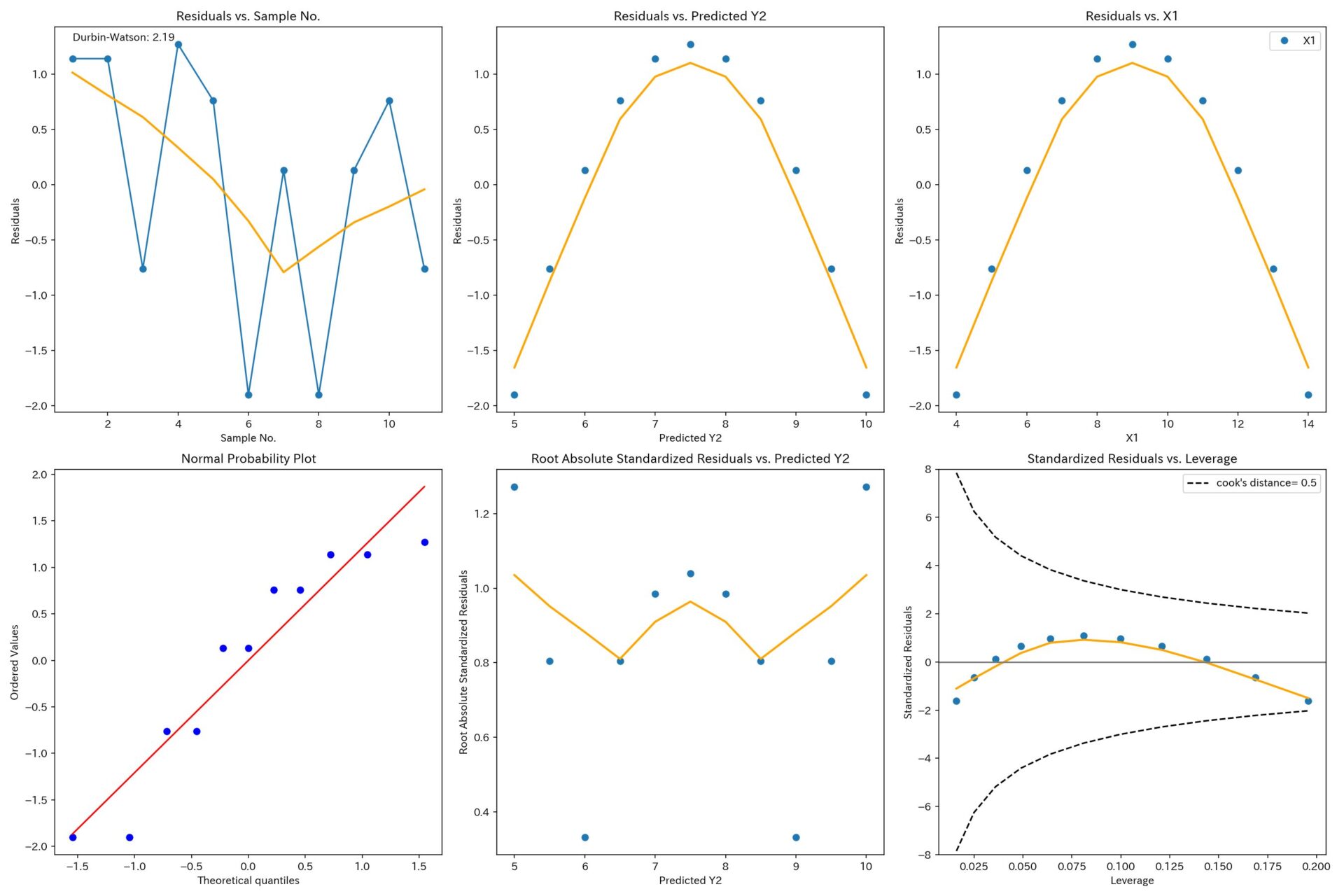
誤差項の正規性の仮定は満たしてそうですが、非線形の関係性が見て取れます。
非線形の変動を表現できるように、説明変数の改良が必要ですね。
X1とY3
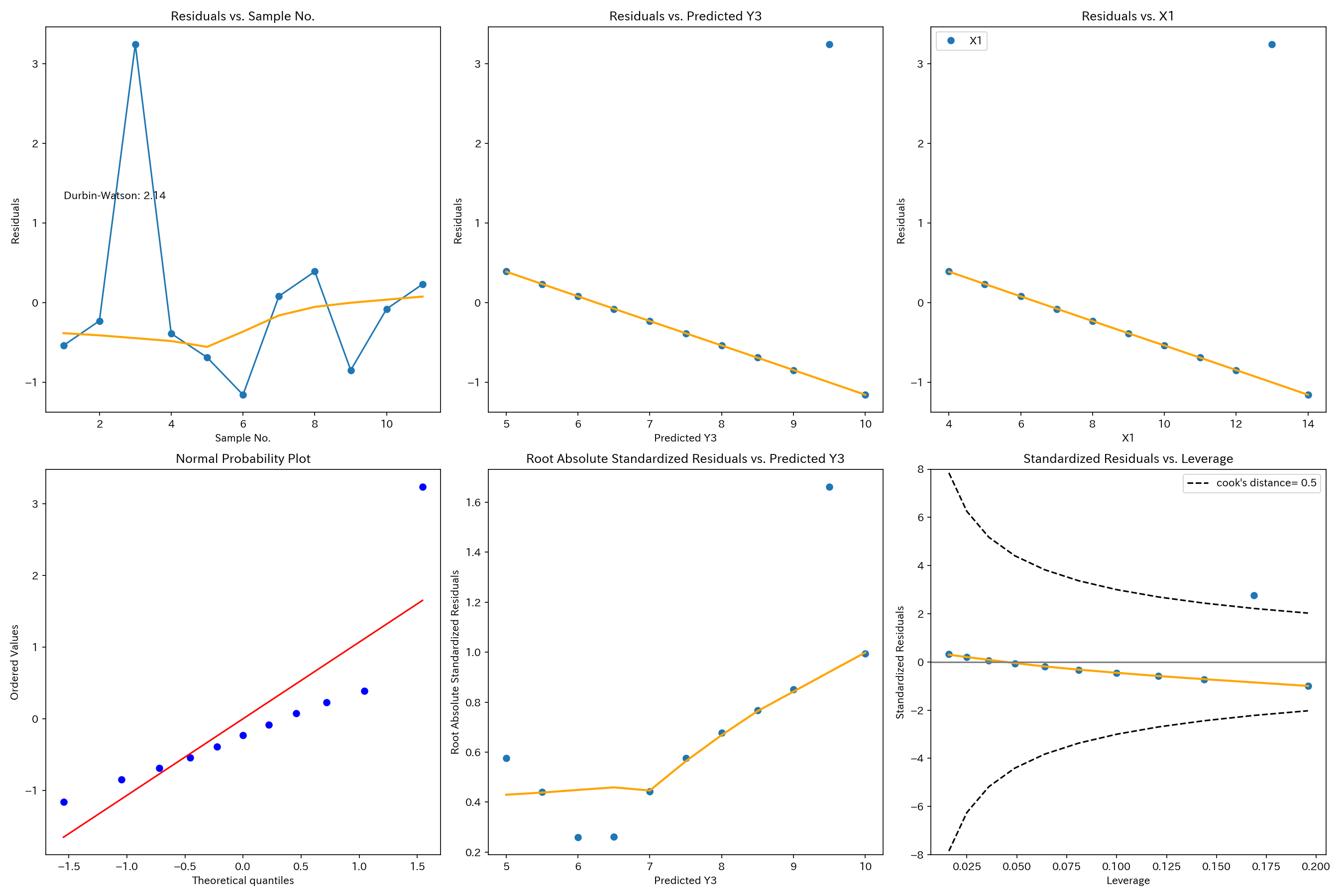
Cookの距離が0.5を超える点があり、外れ値の存在が認められます。
外れ値に適切に対処してから回帰分析を行う必要があります。
X2とY4
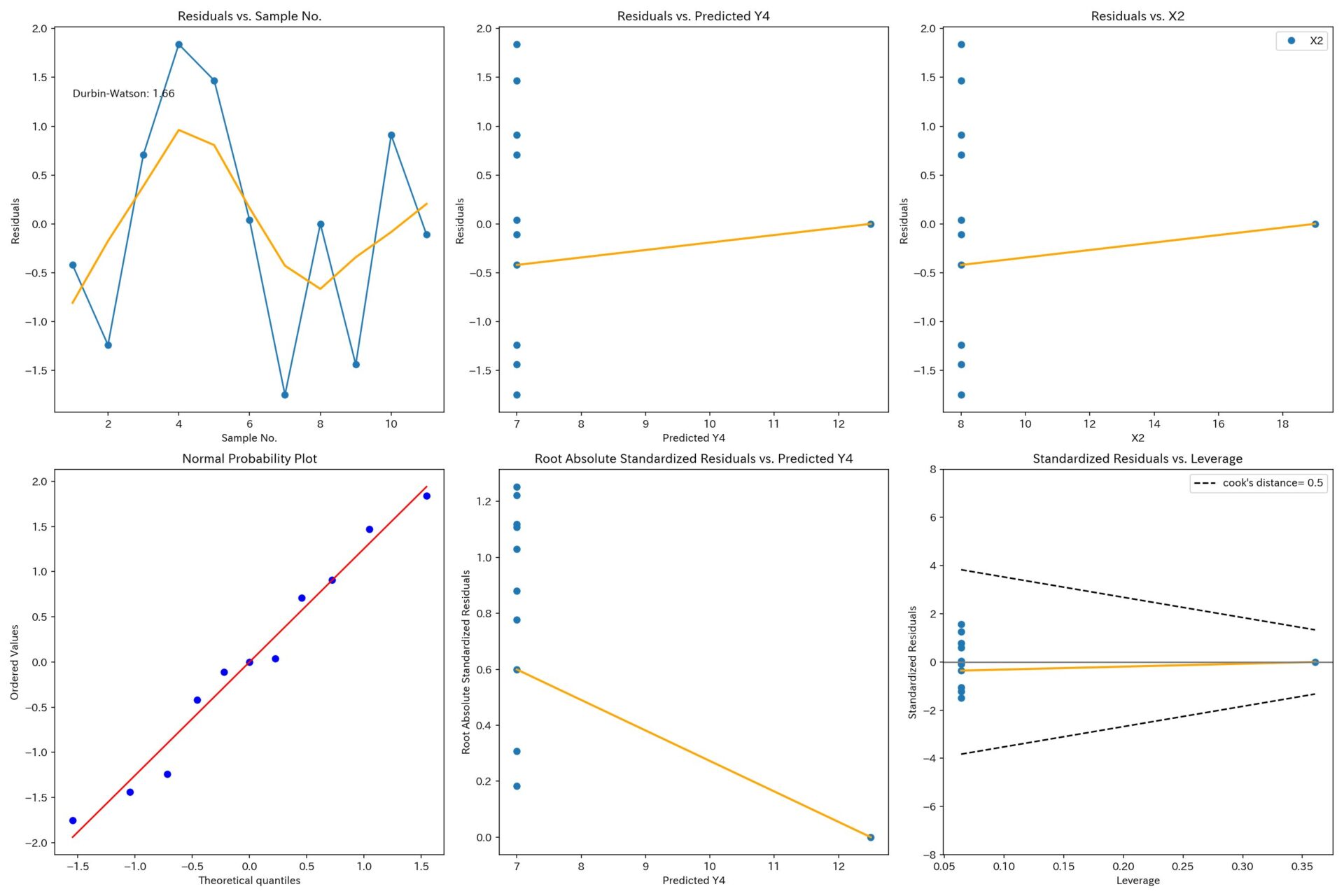
てこ比(Leverage)が1点だけ異常に大きく、回帰モデルはこの1点に引っ張られています。
ちなみに、この1点を除くとxは変化しないので回帰分析はできません。
実務で非常によくある悪いパターンです。
こんな回帰モデルを根拠として、テストや設備投資をし、失敗してしまう例を何度か見てきました。
【参考】pythonコード
上記の残差分析を行うpythonコードを参考に載せておきます。
コチラのGitHubにも載せています。
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
import statsmodels.api as sm
from scipy import stats
import seaborn as sns
# サンプルデータ(アンスコムの数値例)
X1 = np.array([10, 8, 13, 9, 11, 14, 6, 4, 12, 7, 5])
Y1 = np.array([8.04, 6.95, 7.58, 8.81, 8.33, 9.96, 7.24, 4.26, 10.84, 4.82, 5.68])
Y2 = np.array([9.14, 8.14, 8.74, 8.77, 9.26, 8.10, 6.13, 3.10, 9.13, 7.26, 4.74])
Y3 = np.array([7.46, 6.77, 12.74, 7.11, 7.81, 8.84, 6.08, 5.39, 8.15, 6.42, 5.73])
X2 = np.array([8, 8, 8, 8, 8, 8, 8, 19, 8 ,8 ,8])
Y4 = np.array([6.58, 5.76, 7.71, 8.84, 8.47, 7.04, 5.25, 12.5, 5.56, 7.91, 6.89])
def residuals_analysis_plots(X, Y, Xlabel, Ylabel, filename):
X = X.reshape(-1, 1)
# 線形回帰モデルの構築とフィッティング
model = LinearRegression()
model.fit(X, Y)
# 回帰直線の描画
plt.scatter(X, Y, color='blue')
plt.plot(X, model.predict(X.reshape(-1, 1)), color='red')
plt.xlabel(Xlabel)
plt.ylabel(Ylabel)
# x軸とy軸の範囲と間隔を指定
plt.xticks(np.arange(0, 21, 5), fontsize=12)
plt.yticks(np.arange(0, 16, 5), fontsize=12)
#plt.title('Linear Regression for Y1')
# 回帰係数、切片、決定係数の値を取得
coefficients = model.coef_
intercept = model.intercept_
r_squared = model.score(X.reshape(-1, 1), Y)
# 回帰係数、切片、決定係数をグラフ内に書き込む
plt.text(3, 13, f'Regression Coefficients: {coefficients[0]:.2f}', fontsize=10, color='black')
plt.text(3, 12, f'Intercept: {intercept:.2f}', fontsize=10, color='black')
plt.text(3, 11, f'R-squared: {r_squared:.2f}', fontsize=10, color='black')
# グラフをPNGファイルとして保存
plt.savefig(rf'./linear_regression_plot_{filename}.png', facecolor='white', dpi=150)
plt.show()
# Yの推定値
Y_pred = model.predict(X)
# 残差
residuals = Y - Y_pred
# 標準化された残差
standardized_residuals = residuals / np.std(residuals, ddof=1)
# レバレッジ(てこ比)の計算
H = X @ np.linalg.inv(X.T @ X) @ X.T
leverage = np.diag(H)
# クックの距離の計算
cook_distance = (standardized_residuals ** 2) * leverage / (1 - leverage) / X.shape[0]
# クックの距離が0.5と1になる標準化残差を逆算
standardized_residual_05 = np.sqrt(0.5 * (1 - leverage)/ leverage * (X.shape[1] + 1))
standardized_residual_1 = np.sqrt(1 * (1 - leverage)/ leverage * (X.shape[1] + 1))
# leverageとstandardized_residual_05を結合して2次元のnumpy配列を作成
data = np.column_stack((leverage, standardized_residual_05, -standardized_residual_05))
# xに関してソート
sorted_data = data[data[:,0].argsort()]
# ダービン・ワトソン統計量の計算
residuals_diff = np.diff(residuals)
dw_statistic = np.sum(residuals_diff**2) / np.sum(residuals**2)
# グラフの作成
plt.figure(figsize=(18, 12))
# グラフ1: サンプルNo.を横軸として、残差eをプロット
plt.subplot(2, 3, 1)
plt.plot(np.arange(1, 12), residuals, 'o-')
plt.xlabel('Sample No.')
plt.ylabel('Residuals')
plt.text(1, 1.3, f'Durbin-Watson: {dw_statistic:.2f}', fontsize=10, color='black')
plt.title('Residuals vs. Sample No.')
# LOWESS平滑化の線を追加
lowess_results = sm.nonparametric.lowess(residuals, np.arange(1, 12))
plt.plot(lowess_results[:,0], lowess_results[:, 1], color='orange', linewidth=2)
# グラフ2: Yの推定値を横軸として、残差eをプロット
plt.subplot(2, 3, 2)
plt.plot(Y_pred, residuals, 'o')
plt.xlabel(f'Predicted {Ylabel}')
plt.ylabel('Residuals')
plt.title(f'Residuals vs. Predicted {Ylabel}')
# LOWESS平滑化の線を追加
lowess_results = sm.nonparametric.lowess(residuals, Y_pred)
lowess_results_sorted = lowess_results[lowess_results[:, 0].argsort()]
plt.plot(lowess_results_sorted[:, 0], lowess_results_sorted[:, 1], color='orange', linewidth=2)
# グラフ3: Xを横軸として、残差eをプロット
plt.subplot(2, 3, 3)
plt.plot(X, residuals, 'o', label=Xlabel)
plt.xlabel(Xlabel)
plt.ylabel('Residuals')
plt.title(f'Residuals vs. {Xlabel}')
plt.legend()
# LOWESS平滑化の線を追加
lowess_results = sm.nonparametric.lowess(residuals, X[:,0])
lowess_results_sorted = lowess_results[lowess_results[:, 0].argsort()]
plt.plot(lowess_results_sorted[:,0], lowess_results_sorted[:, 1], color='orange', linewidth=2)
# グラフ4: 残差eの正規確率プロット
plt.subplot(2, 3, 4)
stats.probplot(residuals, dist="norm", plot=plt)
plt.title('Normal Probability Plot')
# グラフ5: 標準化された残差の絶対値の平方根をy軸とし、Yの推定値をx軸とするグラフ
plt.subplot(2, 3, 5)
plt.plot(Y_pred, np.sqrt(np.abs(standardized_residuals)), 'o')
plt.xlabel(f'Predicted {Ylabel}')
plt.ylabel('Root Absolute Standardized Residuals')
plt.title(f'Root Absolute Standardized Residuals vs. Predicted {Ylabel}')
# LOWESS平滑化の線を追加
lowess_results = sm.nonparametric.lowess(np.sqrt(np.abs(standardized_residuals)), Y_pred)
lowess_results_sorted = lowess_results[lowess_results[:, 0].argsort()]
plt.plot(lowess_results_sorted[:, 0], lowess_results_sorted[:, 1], color='orange', linewidth=2)
# グラフ6: レバレッジをx軸に、標準化された残差をy軸とするグラフ
plt.subplot(2, 3, 6)
plt.plot(leverage, standardized_residuals, 'o')
plt.xlabel('Leverage')
plt.ylabel('Standardized Residuals')
plt.title('Standardized Residuals vs. Leverage')
# LOWESS平滑化の線を追加
lowess_results = sm.nonparametric.lowess(standardized_residuals, leverage)
lowess_results_sorted = lowess_results[lowess_results[:, 0].argsort()]
plt.plot(lowess_results_sorted[:, 0], lowess_results_sorted[:, 1], color='orange', linewidth=2)
# クックの距離を点線で表示
plt.axhline(y=0, color='gray', linestyle='-')
plt.plot(sorted_data[:, 0], sorted_data[:, 1], '--',color='black', label="cook's distance= 0.5")
plt.plot(sorted_data[:, 0], sorted_data[:, 2], '--', color='black')
plt.ylim([-8, 8])
plt.legend()
plt.tight_layout()
# グラフをPNGファイルとして保存
plt.savefig(rf'./residuals_analysis_plot_{filename}.png', facecolor='white', dpi=150)
plt.show()
#残差分析を実行
residuals_analysis_plots(X1, Y1, Xlabel='X1', Ylabel='Y1', filename='X1_Y1')
residuals_analysis_plots(X1, Y2, Xlabel='X1', Ylabel='Y2', filename='X1_Y2')
residuals_analysis_plots(X1, Y3, Xlabel='X1', Ylabel='Y3', filename='X1_Y3')
residuals_analysis_plots(X2, Y4, Xlabel='X2', Ylabel='Y4', filename='X2_Y4')
参考文献
統計検定準1級の参考書です。
「第17章 回帰診断法」で、図や例題を使ってわかりやすく解説してくれてます。
小難しい数式もほとんどなく、残差分析(回帰診断法)の概要をつかむのに最適です。
回帰分析の決定版とも言える教科書です。
上記の「統計学実践ワークブック」に記載されていない内容にも触れています。
残差分析の威力がすっと理解できる「アンスコムの数値例」が紹介されており、本記事でも使わせてもらいました。
