どうも。こんにちは。
ケミカルエンジニアのこーしです。
本日は、「プロセスデータの平滑化(savgol_filter)」についてわかりやすく解説します。
平滑化は、ノイズを含むデータから有益な情報を取り出す重要なデータの前処理です。
本記事では、Savitzky-Golay法という平滑化手法を紹介し、最適な平滑化パラメータの決定方法について具体的に解説していきます。
本記事の内容
・平滑化とは
・Savitzky-Golayフィルタ
・平滑化パラメータの決定方法
・参考文献
この記事を書いた人

こーし(@mimikousi)
目次
平滑化とは
平滑化は、データ解析の前処理として重要な操作であり、下記3つの目的で行います。
平滑化の目的
-
ノイズの除去:
データは、測定誤差やその他のランダムな要因によりノイズが混じっているため、平滑化により変動を抑制し、データの本質的なパターンを見えやすくする。 -
トレンドの抽出:
時間経過に伴う変化や周期性など、データの基本的な動向(トレンド)を見つけ、将来の動向を予測するのに役立つ。 -
データの視覚化:
データを視覚的に理解する際に、平滑化によりノイズを除去するとデータの概観を捉えやすくなる。
特に、製造業のプロセスデータにおいては品質管理・プロセス最適化、設備保全と予兆管理において下記のような効果が得られます。
-
品質管理:
プロセスのパラメータや環境条件の変動、そして分析誤差などにより、品質データは揺らぐため、平滑化により本質的なトレンドや異常を見つけやすくなる。 -
プロセス最適化:
ノイズを除去することで、各運転条件(パラメータ)とプロセス変動の関係を把握することができ、最適な運転条件を決定できる。 -
設備保全と予兆管理:
センサデータを平滑化することで、異常パターンや予兆を早期に発見し、生産停止による損失を防ぐことができる。
平滑化の種類
平滑化にもいくつかの手法があります。
代表的な平滑化手法は下記の通りです。
平滑化手法
- 単純移動平均
- 線形加重移動平均
- 指数加重移動平均
- Savitzky-Goley法
本記事では、平滑化と微分を同時に行うことができる「Savitzky-Goley(SG)法」について具体的に解説します。
解説記事はコチラ
サンプルデータの入手
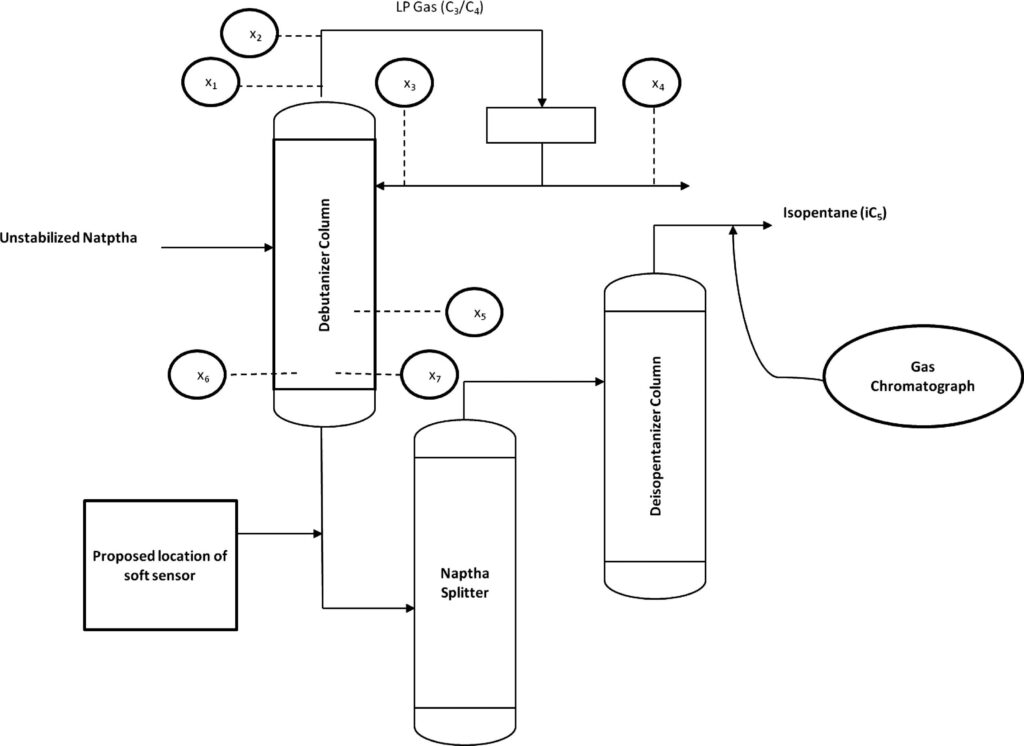
コチラのgithubページで入手できる「debutanizer_data.csv」を利用します。
脱ブタン塔のプロセスデータであり、プロセスフローは上図の通りです。
説明変数がx1〜x7の7個で、目的変数がyの1個、サンプル数は2394個です。
| 変数名 | 詳細 | 日本語訳 |
|---|---|---|
| x1 | Top Temperature | 塔頂温度 |
| x2 | Top pressure | 塔頂圧力 |
| x3 | Reflux flow | 還流流量 |
| x4 | Flow to next process | 次プロセスへの流量 |
| x5 | 6th tray Temperature | 6段目温度 |
| x6 | Bottom Temperature1 | 塔底温度1 |
| x7 | Bottom Temperature2 | 塔底温度2 |
| y | Butane(C4) content in the debutanizer column bottom | 塔底におけるブタン含有量 |
データの読み込み
「debutanizer_data.csv」と同じフォルダに、「smoothing_savgol.ipynb」というファイルを作成しましょう。
下記のコードでライブラリのインポートと、データの読み込みを行います。
簡単な前処理として、目的変数yの測定時間を考慮し、5行だけずらしておきましょう。
import pandas as pd
import numpy as np
import scipy as sp
from scipy import signal
import matplotlib.pyplot as plt
import japanize_matplotlib
import seaborn as sns
sns.set(font='IPAexGothic')
from matplotlib.backends.backend_pdf import PdfPages #pdfで保存する
#脱ブタン塔のプロセスデータを読み込む
df = pd.read_csv('debutanizer_data.csv')
# 目的変数の測定誤差を考慮
df['y'] = df['y'].shift(5)
#yがnanとなる期間のデータを削除
df = df.dropna()
#インデックスをリセット
df = df.reset_index(drop=True)
pythonによるデータの平滑化
pythonには便利なライブラリが豊富にあり、これらを用いれば簡単にデータの平滑化ができます。
Savitzky-Goleyフィルタ
早速、Scipyライブラリのsavgol_filterを用いてデータを平滑化してみましょう。
Scipy公式ドキュメントはコチラです。
savgol_filterでは、事前に窓枠の数(window_length)と多項式の次数(polyorder)を決める必要があります。
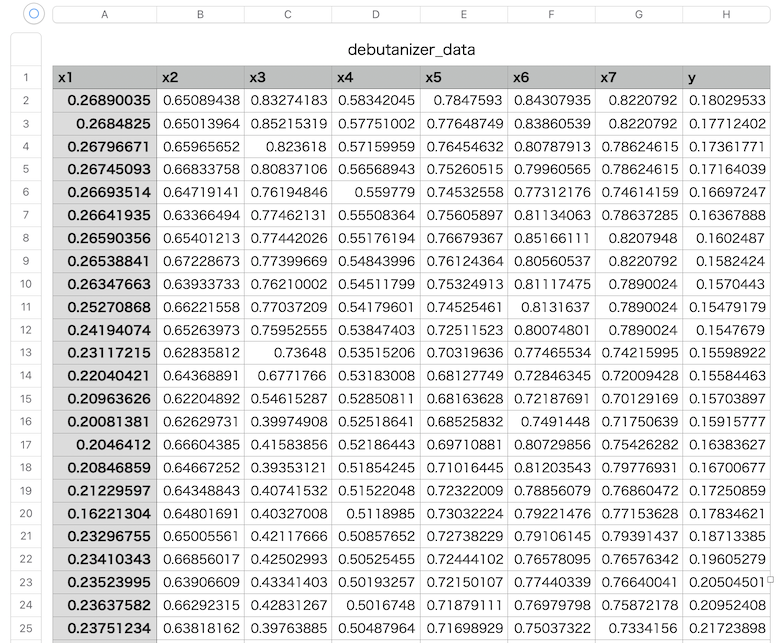
下記のコードで、窓枠の数29、多項式の次数1の平滑化を行いましょう。
# Savitzky-Golayフィルタ
df_sg = pd.DataFrame(index=df.index)
window_length = 29
polyorder = 1
target_column = 'x1'
df_sg[target_column] = signal.savgol_filter(df[target_column], window_length=window_length, polyorder=polyorder)
fig, ax = plt.subplots(figsize=(10,5))
ax.plot(df[target_column], label='original')
ax.plot(df_sg, c='red', label='savgol_filter')
ax.set_ylabel('x1')
ax.text(0.75, 0.91, s=f'polyorder={int(polyorder)}')
ax.text(0.75, 0.97, s=f'window_length={int(window_length)}')
ax.legend(loc='best')
# グラフを保存
fig.savefig(f'{target_column}_trend.png')
plt.show()
注意ポイント
window_lengthは、奇数とする(中央値を定義できないため)polyorderは、window_lengthより小さい数字にする
窓枠の数(window_lenght)の影響
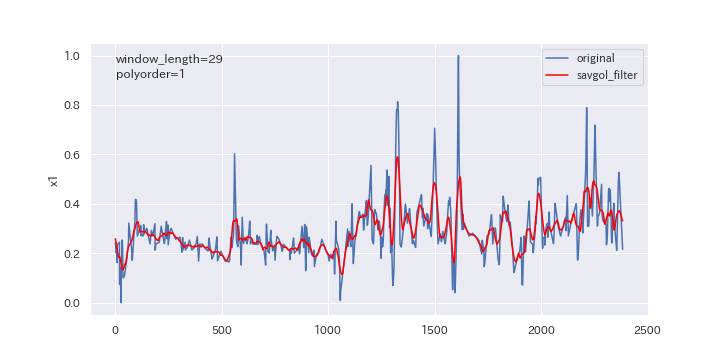
窓枠の数を変更したらどのように変わるのか、確認してみましょう。
window_lengthを5、15、29と変えていきます。
# 空のDataFrameを準備します。ここに平滑化されたデータが保存されます。
df_sg_window = pd.DataFrame()
# Savitzky-Golayフィルタに使用する窓のサイズのリストです。
window_length_list = [5, 15, 29]
# 平滑化を行う特徴量を決めます。
target_column = 'x1'
# 各窓のサイズについてループを行います。
for window_length in window_length_list:
polyorder = 1
# 平滑化したデータを計算し、その結果をDataFrameに新しい列として追加します。
column_name = f'x1_window_length={window_length}'
df_sg_window[column_name] = signal.savgol_filter(df[target_column], window_length=window_length, polyorder=polyorder)
df_sg_x1_window = pd.concat([df[target_column], df_sg_window], axis=1)
#各列のトレンドグラフを作成
for col in df_sg_x1_window.columns:
if col == 'x1':
continue
else:
fig, ax = plt.subplots(figsize=(10,5))
ax.plot(df_sg_x1_window['x1'], label='x1')
ax.plot(df_sg_x1_window[col], label=f'{col}')
ax.set_ylabel('x1')
ax.text(0.75, 0.95, s=f'polyorder={polyorder}')
ax.legend(loc='best')
# グラフを保存
fig.savefig(f'{col}_trend.png')
plt.show()
plt.close(fig)
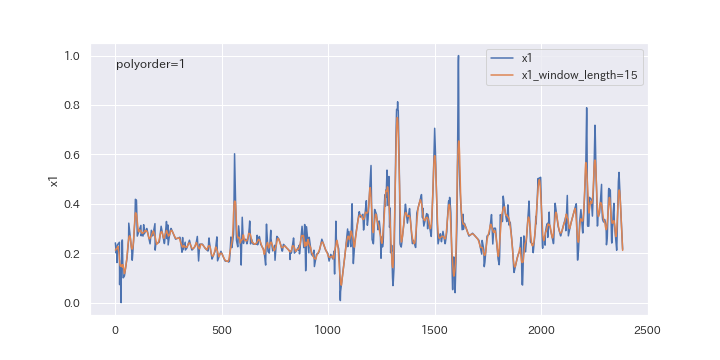
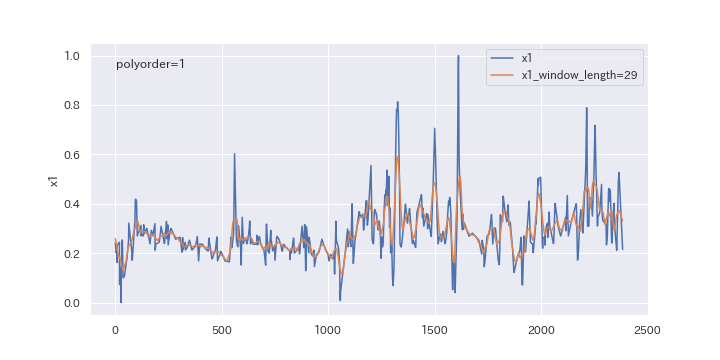
上図を見るとわかるように、窓枠の数(window_length)を大きくすると、より滑らかに平滑化されます。
多項式の次数(polyorder)の影響
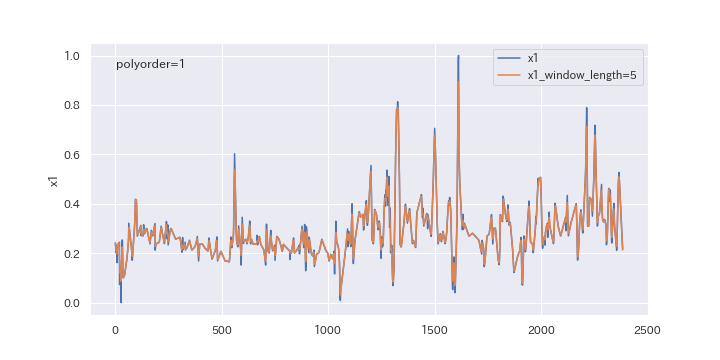
続いて、多項式の次数を変更したらどのように変わるのか、確認してみましょう。
polyorderを0、1、2と変えていきます。
# 空のDataFrameを準備します。ここに平滑化されたデータが保存されます。
df_sg_polyorder = pd.DataFrame()
# Savitzky-Golayフィルタに使用する多項式の次数のリストです。
polyorder_list = range(3)
# 平滑化を行う特徴量を決めます。
target_column = 'x1'
# 次数の数についてループを行います。
for polyorder in polyorder_list:
window_length = 29
# 平滑化したデータを計算し、その結果をDataFrameに新しい列として追加します。
column_name = f'x1_polyorder={polyorder}'
df_sg_polyorder[column_name] = signal.savgol_filter(df[target_column], window_length=window_length, polyorder=polyorder)
df_sg_x1_polyorder = pd.concat([df[target_column], df_sg_polyorder], axis=1)
#各列のトレンドグラフを作成します。
for col in df_sg_x1_polyorder.columns:
if col == 'x1':
continue
else:
fig, ax = plt.subplots(figsize=(10,5))
ax.plot(df_sg_x1_polyorder['x1'], label='x1')
ax.plot(df_sg_x1_polyorder[col], label=f'{col}')
ax.set_ylabel('x1')
ax.text(0.75, 0.95, s=f'window_length={window_length}')
ax.legend(loc='best')
# グラフを保存
fig.savefig(f'{col}_trend.png')
plt.show()
plt.close(fig)
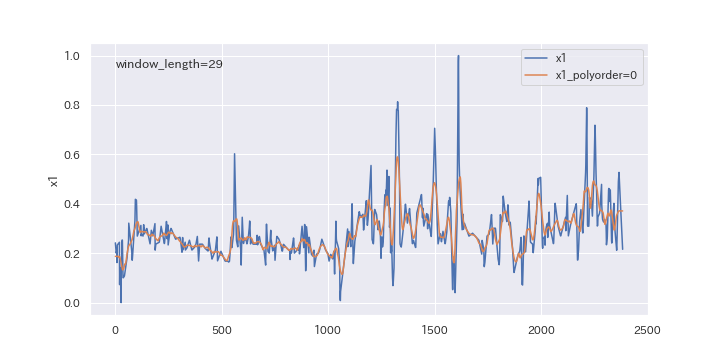
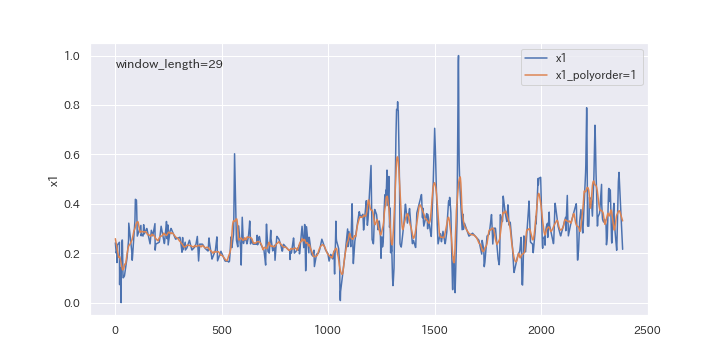
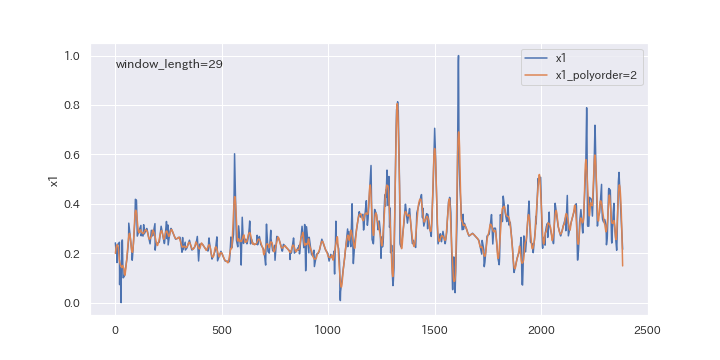
上図を見るとわかるように、多項式の次数(polyorder)を大きくすると、ノイズが強調されやすくなります。
平滑化パラメータの決定方法
savgol-filterの平滑化パラメータ(window_length、polyorder)の決定方法には、下記2つの方法があります。
平滑化パラメータの決定方法
- モデルの検証
回帰や分類モデルの検証において、クロスバリデーション推定値やテストデータにおける予測結果(決定係数R2やRMSE)が最大となるパラメータを選択。
高い推定性能が得られる一方、計算に時間がかかるのがデメリット。 - ノイズの正規性
ノイズが正規分布に従うと仮定すると、平滑化によって減少したノイズ(平滑化前後の差分)の分布も正規分布に従う。
比較的計算は楽だが、モデルの精度が向上するとは限らないのと、微分次数(polyorder)は選択できないのがデメリット。
本記事では、「ノイズの正規性」から平滑化パラメータを決定する方法を紹介します。
具体的には、平滑化前後のデータの差分(ノイズ)に対して「正規性の検定」を行い、p値が最も大きくなる平滑化パラメータを採用します。
# 空のDataFrameを作成し、パラメータを格納するためのインデックスを設定します
df_param = pd.DataFrame(index=['best_window_length', 'best_polyorder', 'best_pvalue'])
# 空のDataFrameを作成し、元のdfのインデックスを使用してインデックスを設定します
df_sg = pd.DataFrame(index=df.index)
# length_maxまでの奇数をリストに入れる
length_max = 30
window_length_list = []
for i in range(3, length_max):
if i % 2 != 0:
window_length_list.append(i)
# savgol_filterのパラメータ探索
for col in df.columns:
# savgol_filterのパラメータを決める
best_window_length = 1
best_polyorder = 0
best_pvalue = 0
# window_length_listをループ
for window_length in window_length_list:
# polyorderを0から2まで1ずつ増やしながらループ
for polyorder in polyorder_list:
#nanを削除
df_col = df[col].dropna()
# savgol_filterで平滑化
y = signal.savgol_filter(df_col, window_length=window_length, polyorder=polyorder)
# normaltestで正規性の検定(ダゴスティーノ・ピアソン検定)
_, pvalue1 = sp.stats.normaltest(df_col - y)
# shapiroで正規性の検定(シャピロ・ウィルク検定)
_, pvalue2 = sp.stats.shapiro(df_col - y)
# kstestで正規生の検定(コルモゴロフ・スミルノフ検定)
# データの平均と標準偏差を計算
mean = df_col.mean()
std = df_col.std(ddof=1)
# 標準正規分布の平均と標準偏差を調整して検定
_, pvalue3 = sp.stats.kstest(df_col, 'norm', args=(mean, std))
# 三つの検定のp値の最小値を取る
pvalue = max(pvalue1, pvalue2, pvalue3) # p値
# p値が最大値を更新したら、best_window_lengthとbest_polyorderを更新する
if pvalue > best_pvalue:
best_window_length = window_length
best_polyorder = polyorder
best_pvalue = pvalue
# savgol_filterのパラメータをDataframeに格納
df_param[col] = [best_window_length, best_polyorder, best_pvalue]
# 平滑化したデータをDataframeに格納
df_sg[col] = signal.savgol_filter(df_col, window_length=best_window_length, polyorder=best_polyorder)
# savgol_filterのパラメータを保存
df_param.to_excel('sg_parameter.xlsx')
# 平滑化したデータを保存
df_sg.to_excel('savgol_filter_data.xlsx')
df_sg.to_pickle('savgol_filter_sgdata.pkl')
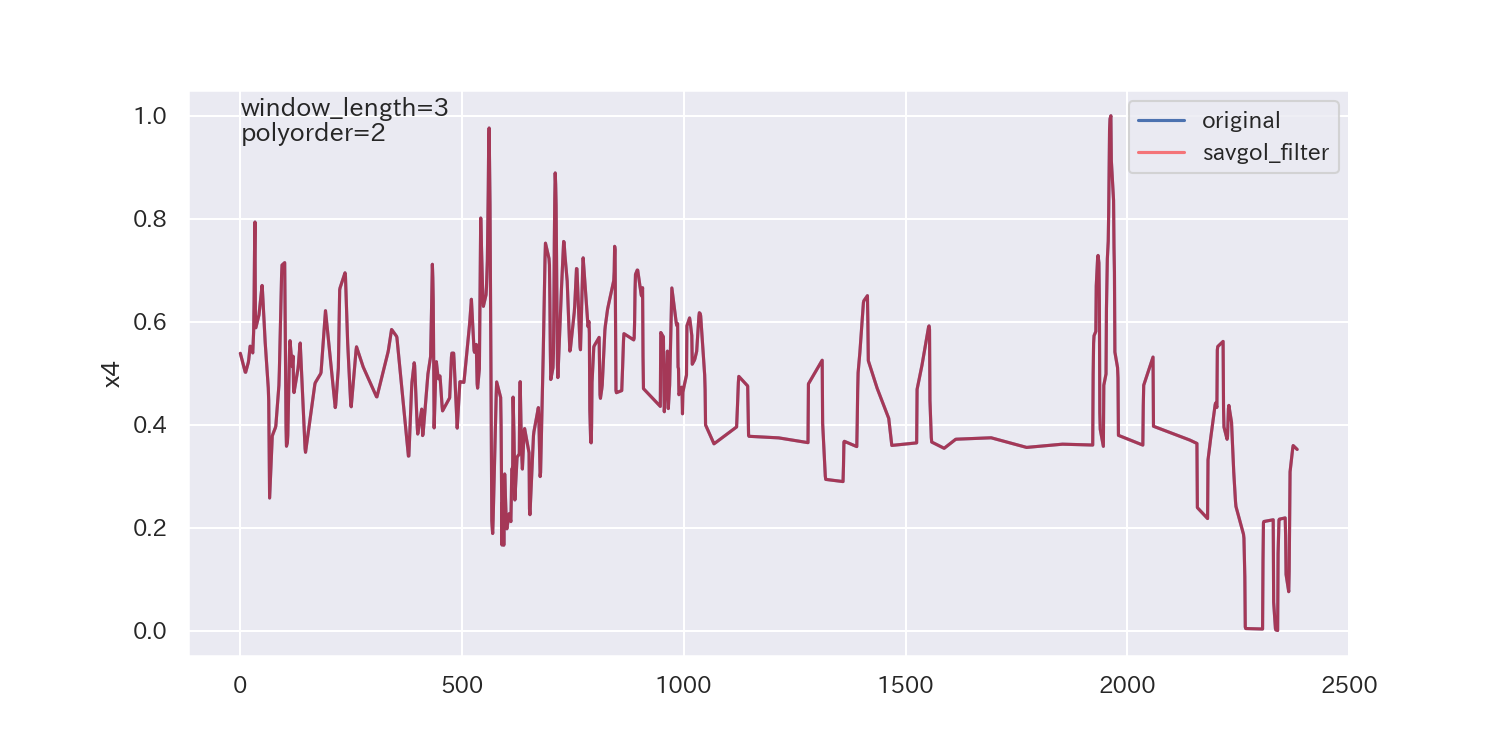
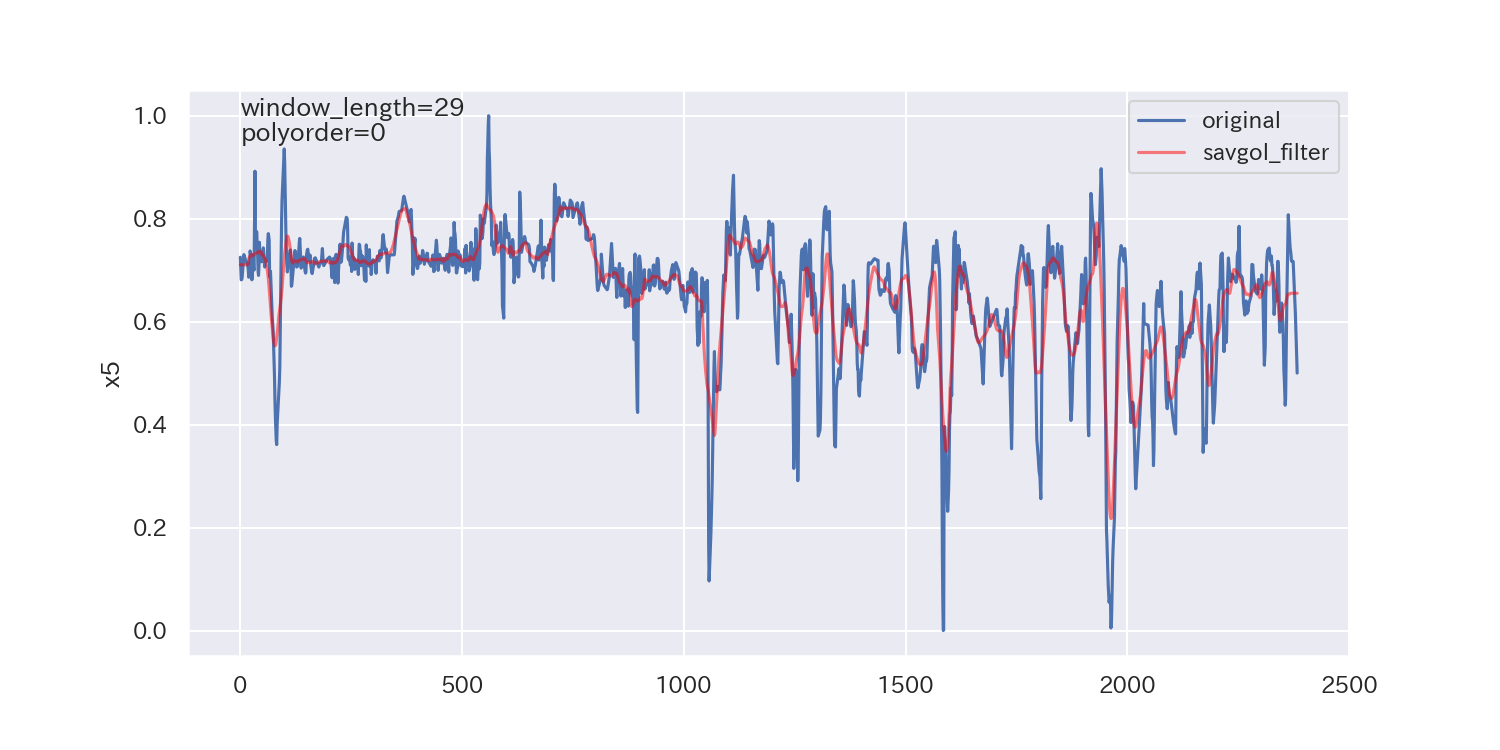
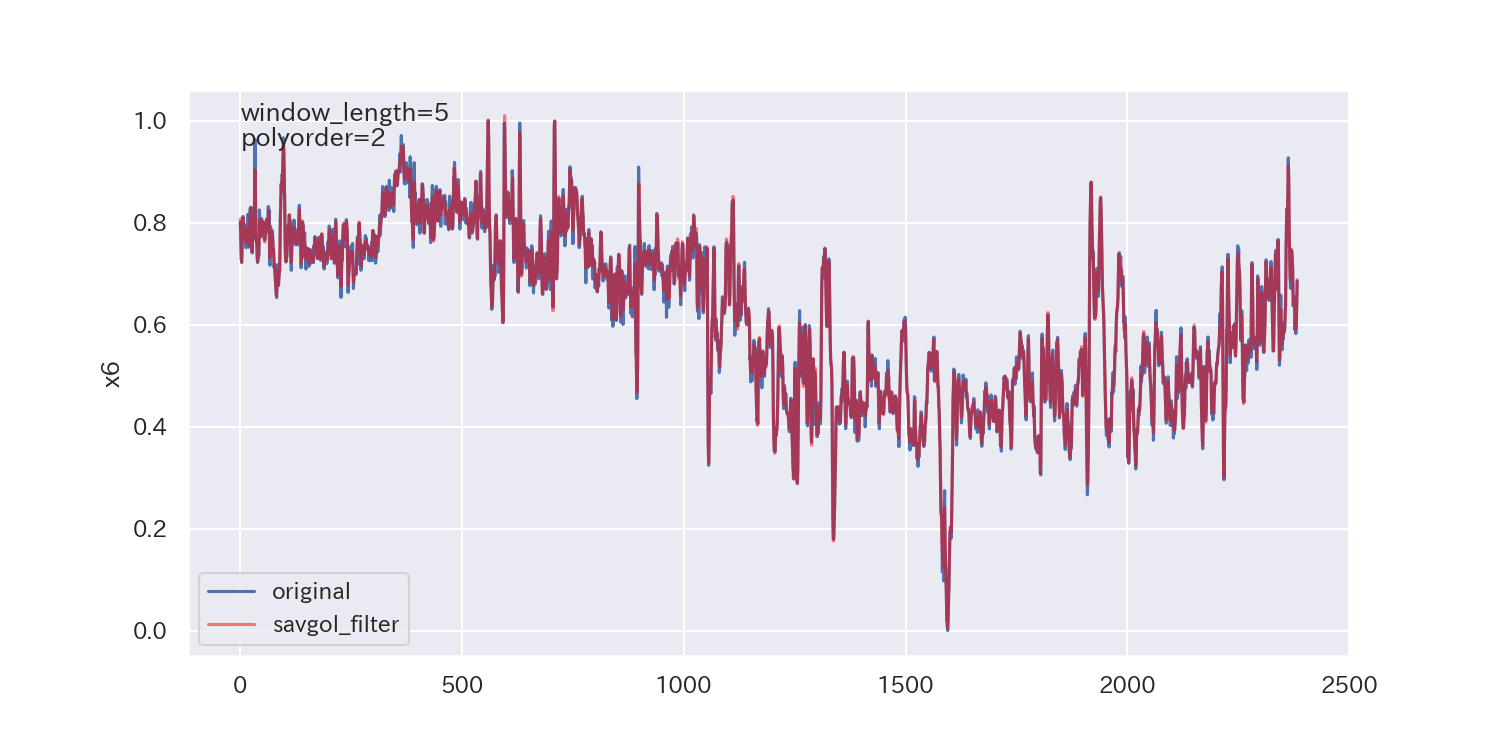
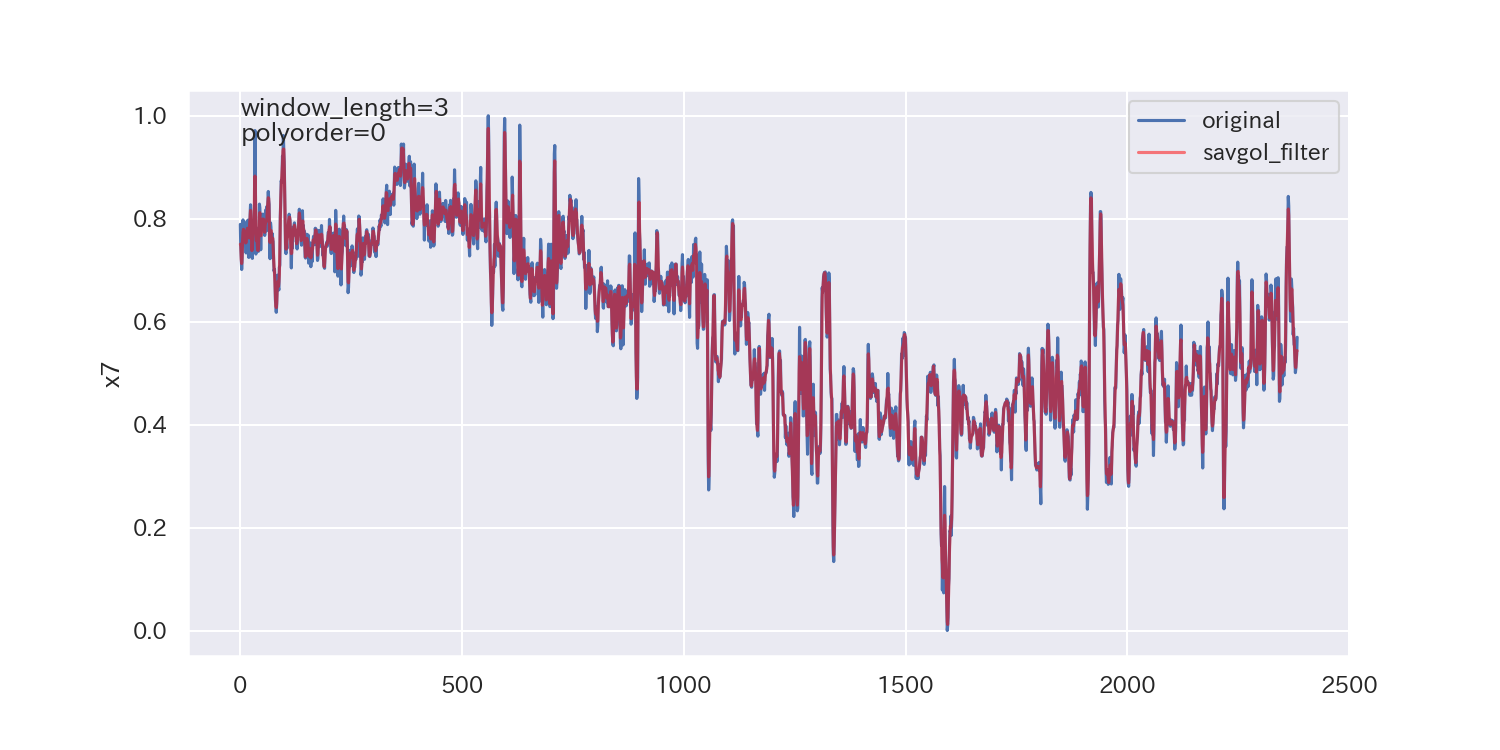
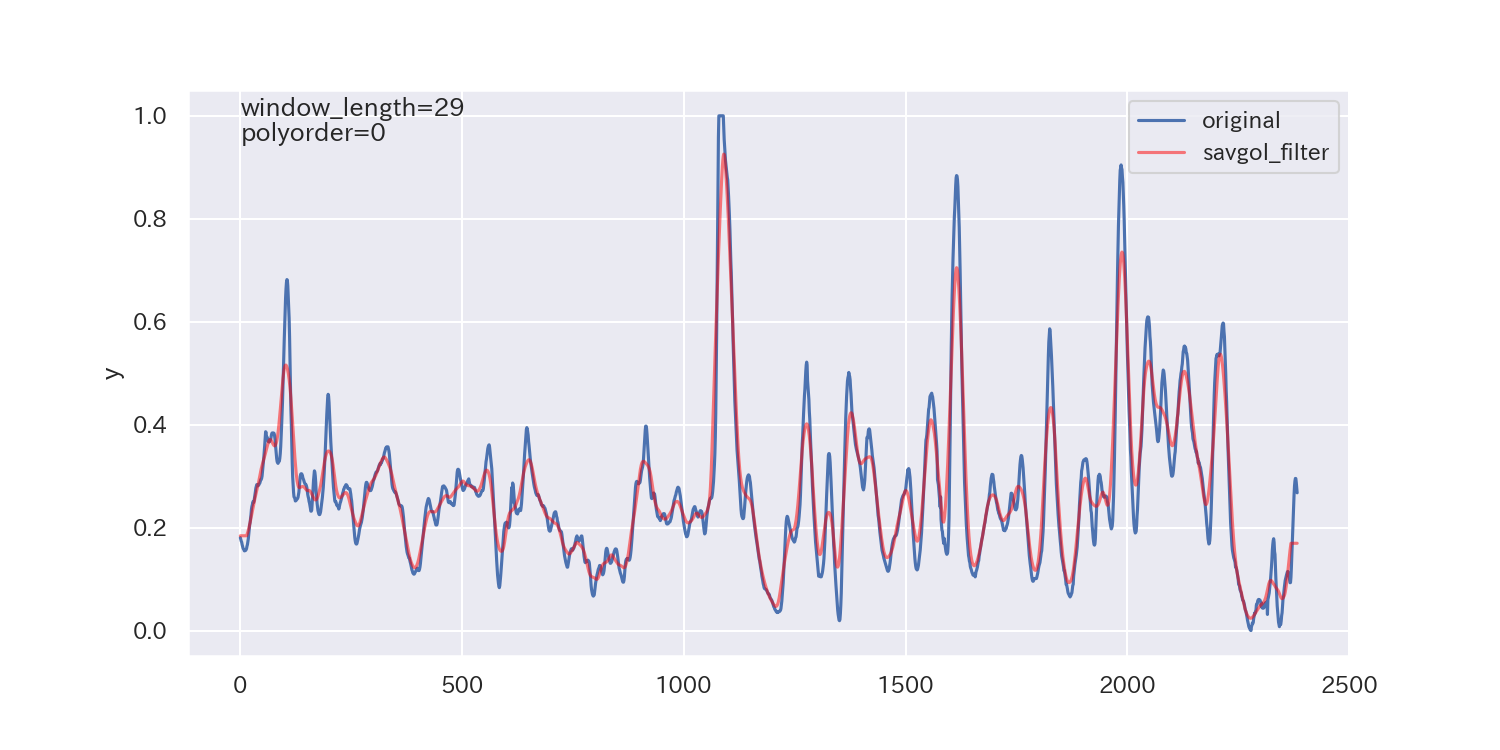
得られた平滑化パラメータは下図の通りです。
p値が小さいので、ノイズが正規分布に従わないことを示しており、最適解とは言えないかもしれません。
ただし、各列で異なる平滑化パラメータが得られています。

平滑化前後の比較
最後に、得られた平滑化パラメータを使って平滑化し、元のデータと比較してみます。
#pdfで保存するためpdfインスタンスを作成
pdf = PdfPages('debutanizer_sg_trend.pdf')
# dfの各列(col)について、トレンドデータを可視化します
for col in df.columns:
# グラフのフィギュア(全体)とその中の描画領域(ax)を作成します
fig, ax =plt.subplots(figsize=(14,5))
# 元のデータ(dfのcol列)をプロットします。
ax.plot(df[col], label='original')
# 平滑化したデータ(df_sgのcol列)をプロットします。透明度(alpha)を0.5として設定します
ax.plot(df_sg[col], color='red', alpha=0.5, label='savgol_filter')
# y軸のラベルを設定します
ax.set_ylabel(col)
ax.text(0.60, 1.00, s=f'window_length={int(df_param[col][0])}')
ax.text(0.60, 0.95, s=f'polyorder={int(df_param[col][1])}')
# 凡例を表示します
ax.legend(loc='best')
# グラフを画面に表示します
plt.show()
# グラフをpdfファイルに保存します
pdf.savefig(fig)
# グラフをpng画像としても保存します
fig.savefig(f'{col}_sg_trend.png', dpi=150)
# メモリの節約と次のループへの準備のため、現在のフィギュアを閉じます
plt.close(fig)
# すべてのグラフを描画し終えたら、pdfファイルを閉じて保存します
pdf.close()
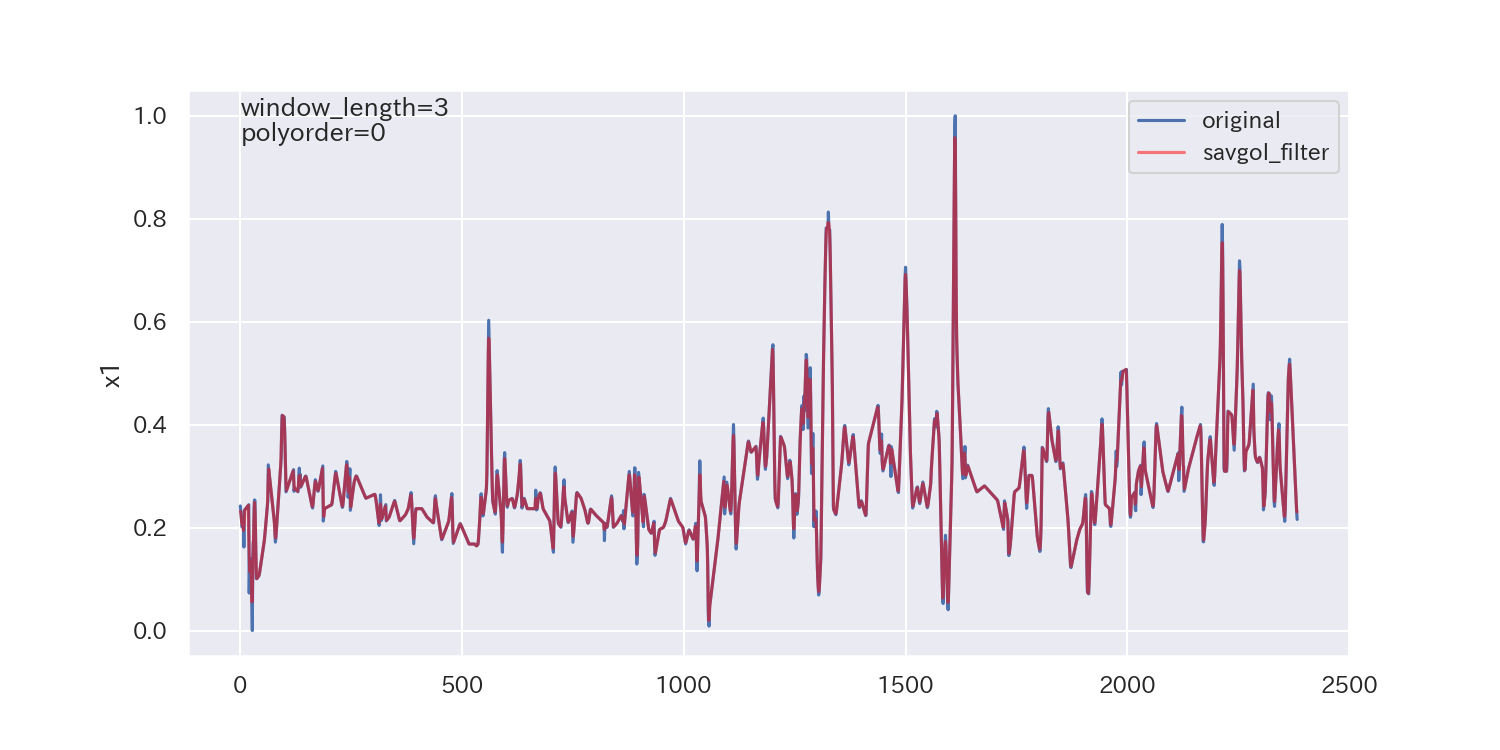
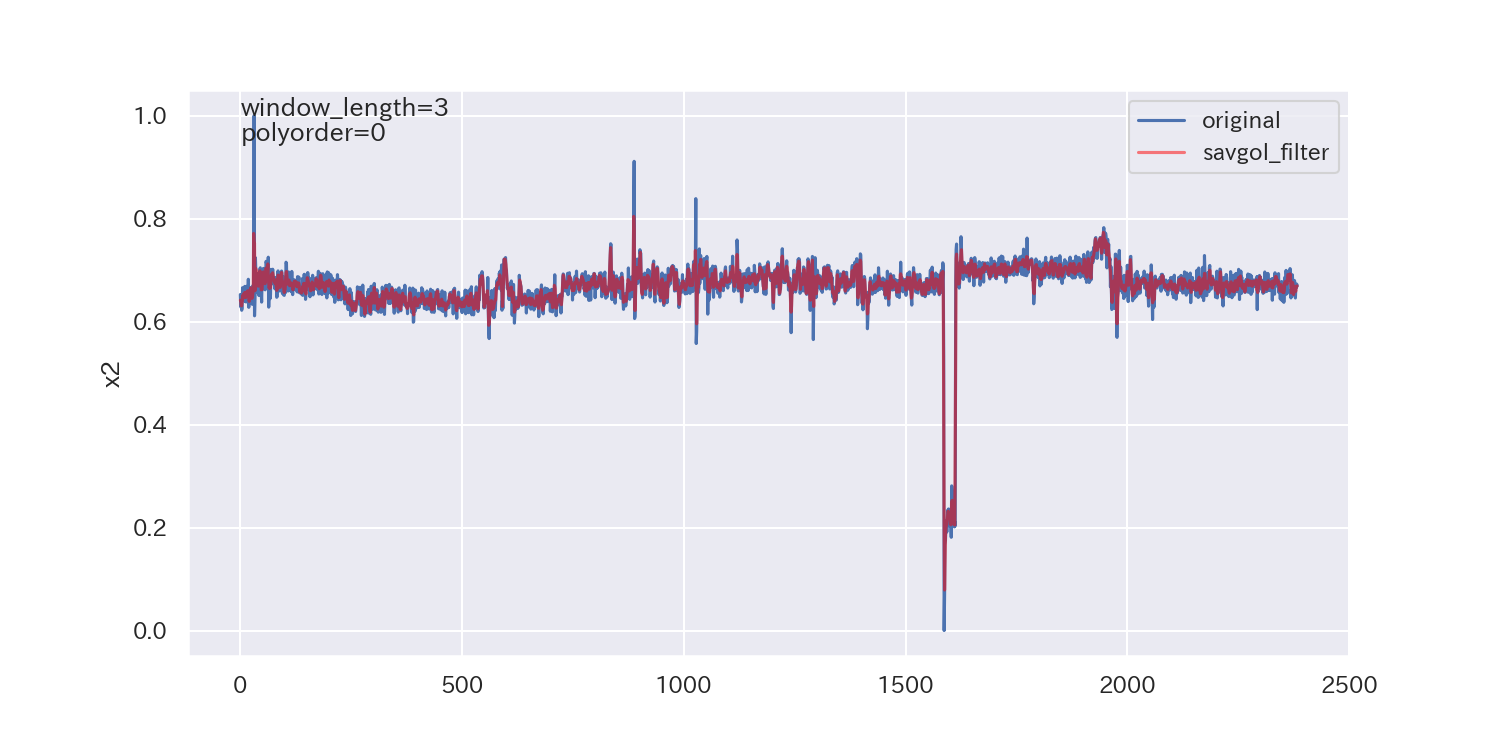
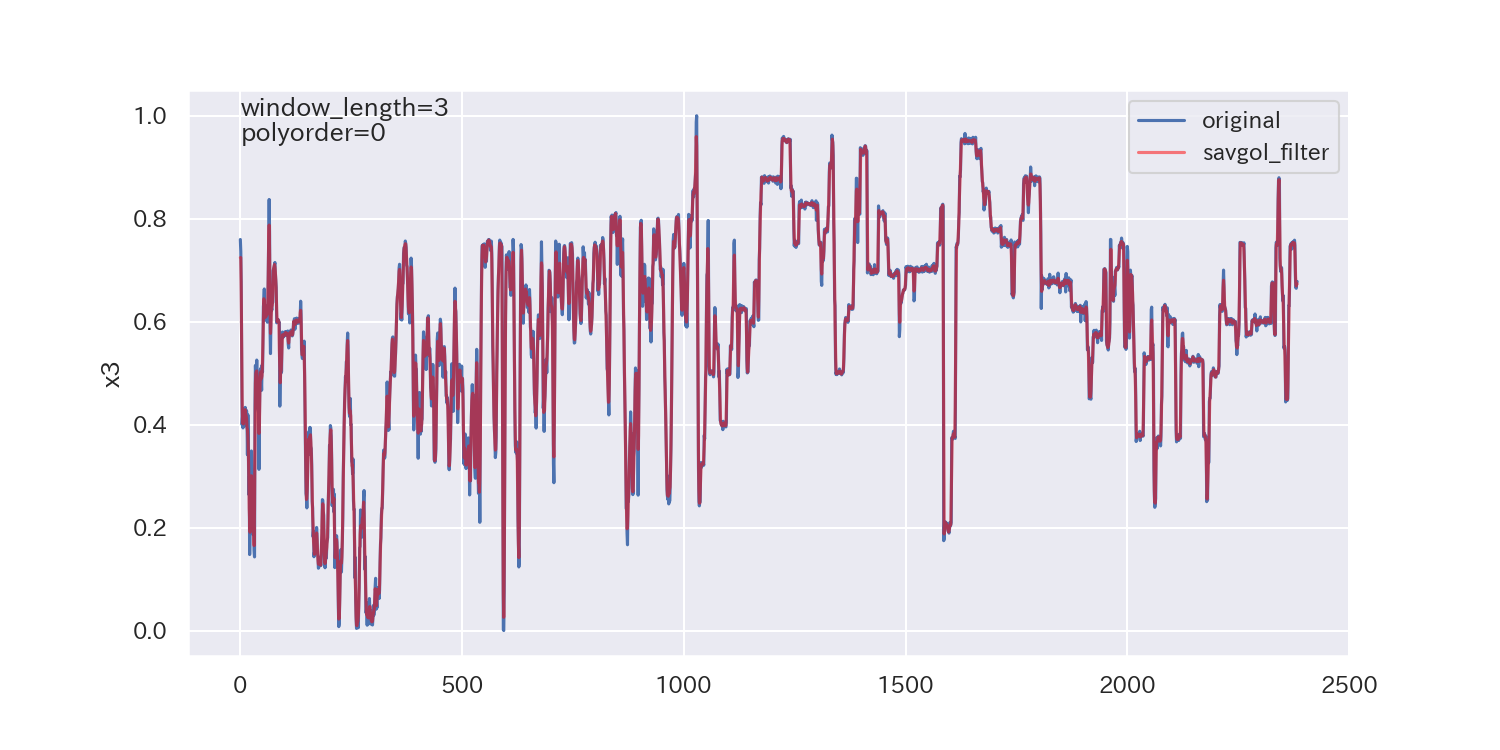
参考文献
化学・化学工学のための実践データサイエンス〜Pythonによるデータ解析・機械学習〜
本記事は主にこちらの書籍を参考にしました。
金子先生の中級者向けの本になります。
発展的な内容が多いため、初心者は前著の下記2冊がオススメです。
機器分析データに対するデータ解析手法について、たくさん紹介されています。
具体的な内容は別途ほかの教科書を参照する必要がありますが、全体像を把握するにはちょうど良い一冊だと思います。
